H型钢梁与矩形钢管柱平齐端板单向螺栓节点承载力性能
李国强, 段 炼, 陆 烨, 张 龙,3, 蒋蕴涵
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.同济大学 土木工程学院,上海 200092;3.华东建筑设计研究院,上海 200002)
在传统的钢框架分析和设计中,为简化分析,通常将框架中的梁柱连接节点部分当作成理想的刚接或者铰接.然而实际工程中的连接节点通常介于这两者之间,属于半刚性连接节点[1].
在20世纪90年代的北岭地震和阪神地震发生后,采用全焊接或者栓焊连接的刚接节点延性较差,梁的上、下翼缘焊缝位置处易发生断裂或翼缘屈曲[2]的问题逐渐被重视起来.而对于端板式半刚性连接节点,震害调查结果表明破坏程度较轻.
端板螺栓连接节点属于典型的半刚性节点[1].在钢框架设计时,由于矩形钢管截面闭合且对称,用作柱时比H型钢或工字型钢有更好的承载性能.但矩形钢管柱和H型钢梁的节点难以采用传统高强螺栓连接,而采用焊接连接的方式则又使得节点现场施工人工量大,质量难以保证,且在地震作用下易发生脆性撕裂破坏,同时不能发挥钢结构快速建造的优势.
本文提出一种H型钢梁与矩形钢管柱采用单向螺栓平齐式端板连接的形式.该种形式的节点采用了特殊的国产自锁式单向螺栓[3],实现了H型钢梁与封闭的矩形管柱的连接.与传统的H型钢梁和矩形钢管柱连接节点相比,可实现快速施工,满足装配化的要求,同时也能改善节点的抗震性能.
进行了6个H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点的单调静力加载试验,详细研究了此类新型节点的承载能力和破坏形式,并结合理论分析,提出了可应用于工程设计的节点承载力的计算公式.
1 试验研究
1.1 试件设计
本文的试件设计和文献[4]的试件设计相同,只是将外伸式端板换为平齐式端板.平齐端板节点的三维示意图见图1,试件节点详图见图2,安装完成后的节点见图3.
共设计3类共计6个试件,试件编号为SR1-1、SR1-2、SR2-1、SR2-2、SR3-1和SR3-2,试件具体参数见表1.通过改变端板厚度或柱壁厚度,期望节点出现3种不同破坏模式,进而得到不同破坏模式下节点抗弯承载力的试验值,进而可用于验证节点承载力理论计算公式的正确性.

图1 H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点示意图Fig.1 Connection schematic diagram
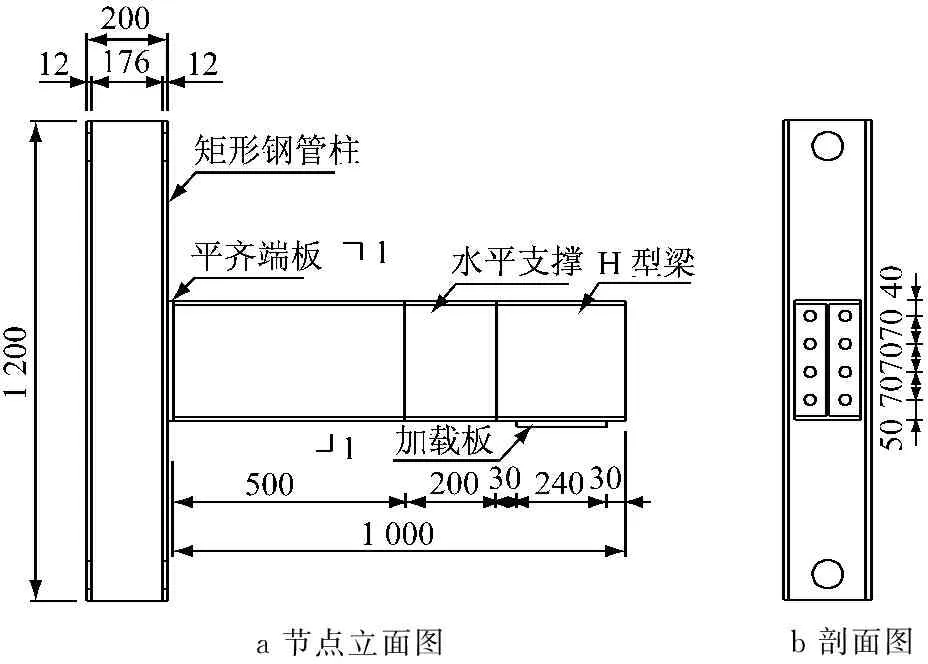
a节点立面图b剖面图

图2 试件节点详图(单位:mm)Fig.2 Dimensions of specimens(unit: mm)

图3 安装完成的节点Fig.3 Connections after installation表1 试件参数表Tab.1 Details of specimens
1.2 材料性能
本文中的试件和文献[4]中的试件为同一加工厂同一批生产加工的试件,故可参考文献[4]获得试验所用钢材、螺栓的力学性能指标.
1.3 试验装置
试验所用试验装置和文献[4]相同,试验加载装置见图4,试验现场布置见图5.
1.4 加载制度
试验的加载制度和文献[4]相同.
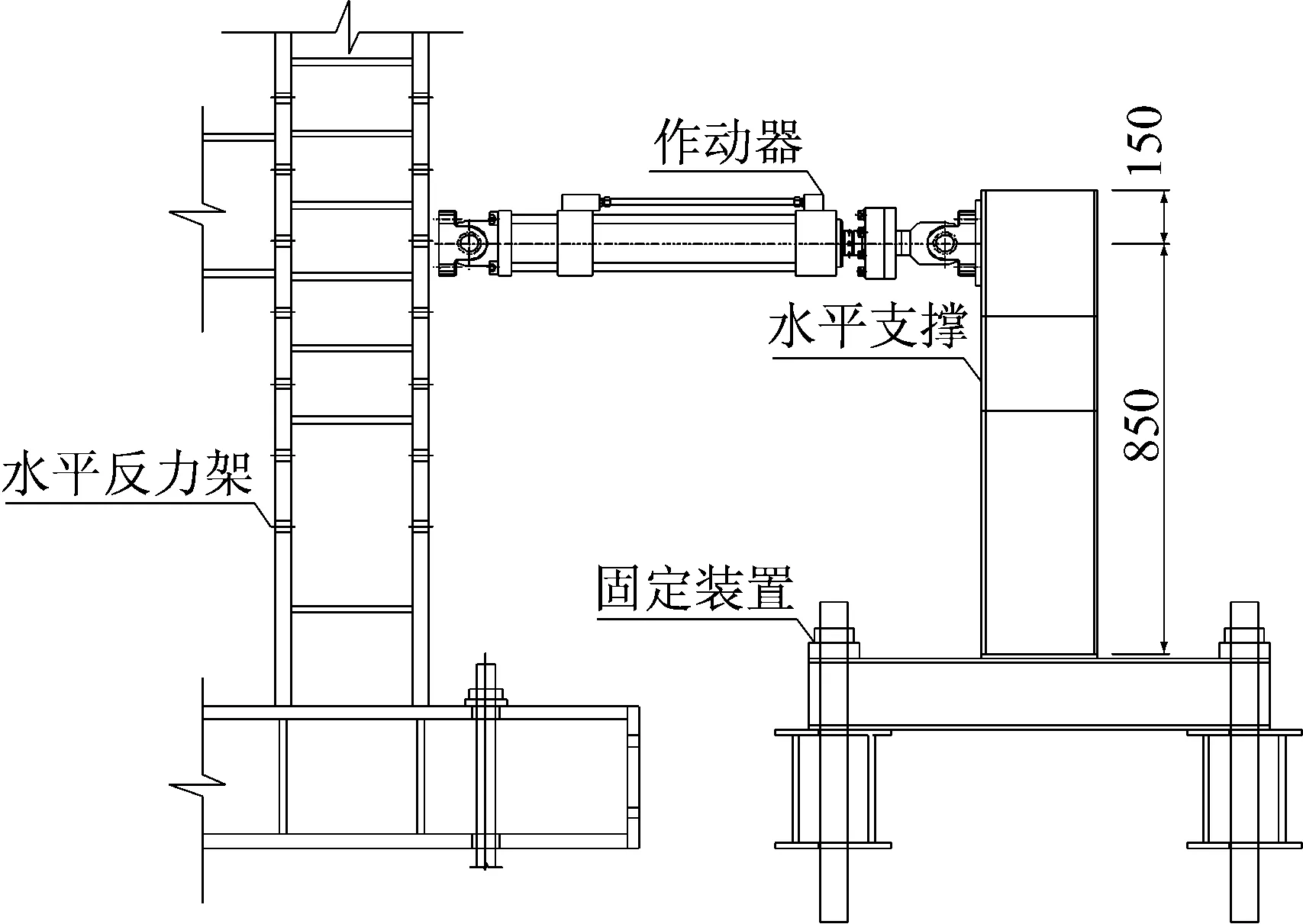
图4 加载装置示意图(单位:mm)Fig.4 Equipment of test setup(unit: mm)

图5 现场试验装置图Fig.5 Schematic diagram of test setup
1.5 测点布置
试验中测点布置方式和文献[4]类似,只是本文中端板为平齐式端板,无外伸段,故将位移计布置在受拉翼缘侧第1排和第2排螺栓处(位移计1—4),而位移计5用于测量受压翼缘处柱壁的变形,如图6所示.
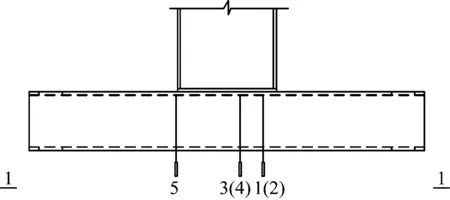
a 位移测点正视图
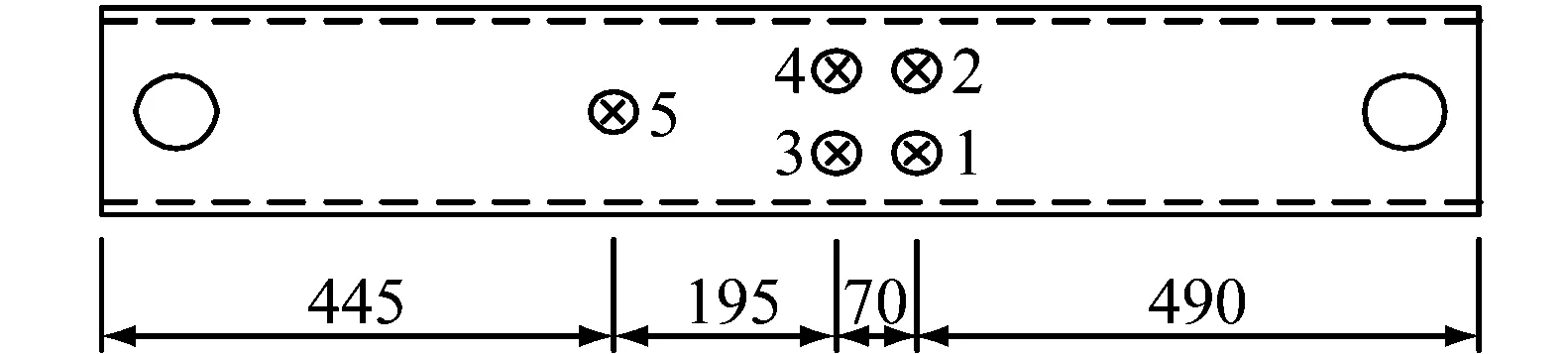
b 截面图图6 位移测点布置图(单位:mm)Fig.6 Arrangement of displacement gauges(unit: mm)
2 试验结果
2.1 弯矩转角曲线
试验过程中记录梁端的水平力和位移,由此可绘制出节点的弯矩-转角关系曲线,见图7.其中,弯矩值为端板与柱翼缘界面处的外加弯矩,可由梁端水平力乘以梁端至端板的距离得到;转角θ为梁柱轴线夹角相对于无荷载时的改变值,可由加载点的水平位移与加载点至端板的距离L之比得到.
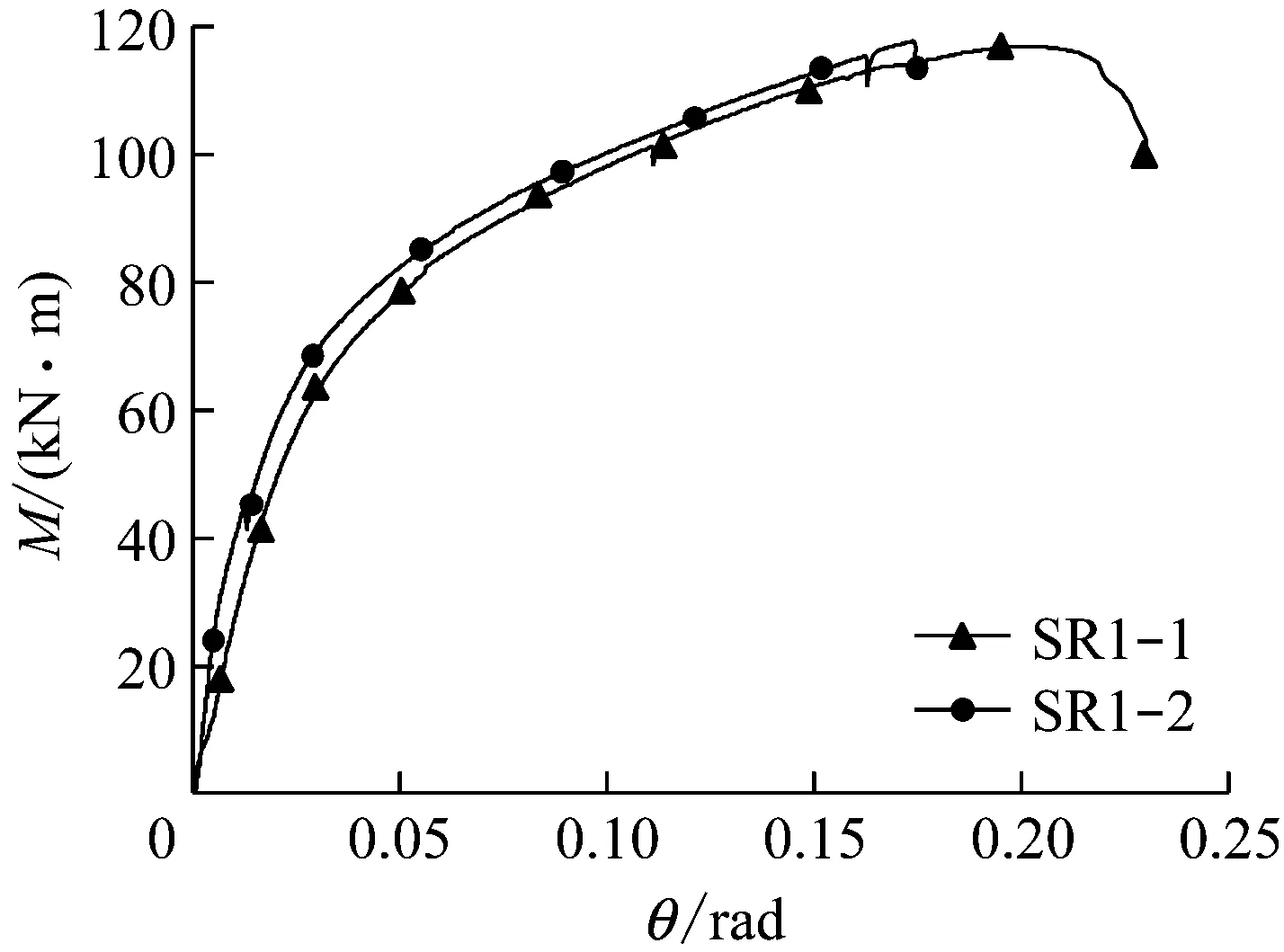
a SR1-1、SR1-2试件

b SR2-1、SR2-2试件

c SR3-1、SR3-2试件图7 试件弯矩转角曲线Fig.7 Rotation-moment curves
2.2 试验现象
本文中的3组试验,各组试验的试验现象和文献[4]中对应组的试验现象相同,各组试验均如预期发生了:单向螺栓拉断、端板屈服破坏或柱壁屈服破坏.表2给出了各个试件的极限承载力及极限位移.各试件破坏形态如图8所示.

表2 各组试件的极限承载力及极限位移Tab.2 Ultimate bearing capacity and ultimatedisplacement of each specimen

a试件SR1-1b试件SR1-2c试件SR2-1d试件SR2-2e试件SR3-1f试件SR3-2
图8试件破坏形态
Fig.8Failurepatterns
3 理论分析
3.1 螺栓强度控制的节点承载力计算
目前各国规范提出的螺栓受拉力作用的计算模型均是针对H型钢梁与H型钢柱端板高强螺栓连接节点,如图9所示[5].以图9a所示的节点为例,图9b—图9f给出了5种计算模型.我国《钢结构高强度螺栓连接技术规程》[6]考虑到平齐式端板连接节点的承载力和转动刚度均比外伸式端板连接节点低很多,故只列出了外伸式端板连接节点.规范中对摩擦型高强螺栓假定端板接触面保持紧密贴合不被拉开,转动中性轴位于螺栓群形心处,如图9b所示.而对于承压型高强螺栓则允许接触面被拉开,螺栓拉力符合线性分布,转动中性轴位于最下排螺栓处[7],如图9c所示.英国规范[8]对传统的三角形分布做了改进,假定受拉翼缘两侧的两排螺栓承担相同的拉力,如图9d所示.美国规范[9]假定钢梁受拉翼缘旁的两排螺栓承担全部的拉力,如图9e所示.欧洲规范[10]的设计思路与其他规范略有不同,先计算简化的等效T形件极限承载力,进而获得可能的螺栓受力分布,如图9f所示.

abcdef
图9各国规范中高强螺栓端板螺栓连接受力分布模式
Fig.9Boltsforcedistributionpattersineach
country’sdesigncodes
在外拉力作用下,螺栓的外套筒在孔壁的挤压下收缩变形,螺栓与柱壁之间发生相对滑动,柱壁与端板分离,螺栓群的转动中性轴下移.由试验现象可知,对于试件SR1-1和SR1-2,在外拉力的作用下,靠近钢梁上翼缘的第一排螺栓变形最大,可见拉力主要由该排螺栓承担.随着拉力的逐渐增大,端板与柱壁间距离增加,中性轴则逐渐下降直至接近梁受压翼缘处.
对H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点,基于试验现象,本文提出以下的螺栓力分布模式:假定连接节点的转动中性轴位于钢梁受压翼缘中心处,弯矩由转动轴以上的螺栓排承担,计算时忽略掉受压翼缘侧螺栓排对外荷载抵抗的有利作用,其余螺栓排按传统线性分布的受力模式,如图10所示,图中M为弯矩.由此可得螺栓破坏模式下节点的抗弯承载力计算公式(1).代入单向螺栓极限拉力值便可得到该种破坏模式下节点的抗弯承载力理论值.将理论计算值与试验值进行对比,见表3.
(1)
式中:Mbt是单向螺栓强度控制下的节点抗弯承载力;Fu,b是单向螺栓抗拉极限承载力;h1、hi分别代表第1排和第i排螺栓到螺栓群转动中心的距离;m为螺栓列数.
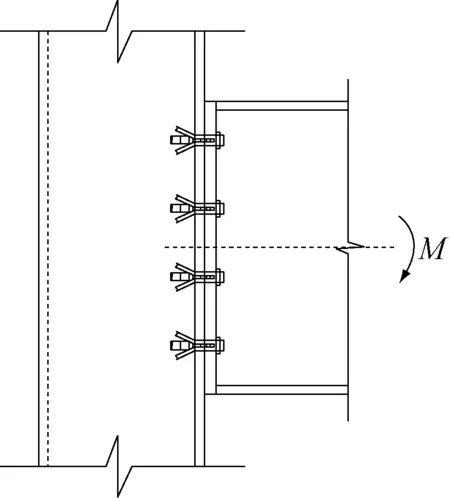

图10 螺栓群受力模式Fig.10 Bolts force distribution pattern表3 SR1-1、SR1-2试件抗弯承载力理论值与试验值比较Tab.3 Comparison of moment resistancebetween theory and test results

试件编号抗弯承载力试验值Mt/(kN·m)抗弯承载力理论值Mc/(kN·m)Mc/MtSR1-1115.5114.70.993SR1-2120.1114.70.955
由表3可知,节点抗弯承载力理论值与试验值很接近,误差在5%以内.
3.2 端板强度控制的节点承载力计算
对于梁柱端板高强螺栓连接节点中端板的承载力, Eurocode 3[10]将各螺栓排所在的端板与钢梁腹板的组合体简化为一T形连接件进行分析,如图11所示.将出现在螺栓周围复杂的屈服线的计算转变为T形件的有效长度leff的计算.通过确定各T形件在可能的破坏模式下的极限承载力,进而得到整个节点的抗弯承载力.

a单排螺栓简化模型b螺栓群简化模型
图11T形连接件
Fig.11EquivalentT-stubs
H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点中端板控制的承载力,也可参考Eurocode 3的研究思路.节点的抗弯承载力取决于简化的等效T形件的极限承载力,而等效T形件的极限承载力又取决于T形件的破坏模式,如图12所示.

a破坏模式1b破坏模式2
图12T形件的破坏模式
Fig.12FailuremodesofT-stubs
T形件可能的破坏模式分别有:① T形件翼缘根部和螺栓位置处屈服;② T形件翼缘根部屈服且螺栓破坏失效.上述两种破坏模式下T形件的抗拉承载力的计算见表4.

表4 T形连接件的抗拉承载力Tab.4 Resistance FT,Ra of a T-stub flange
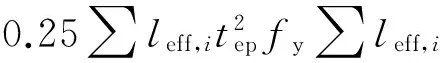
根据试验现象,内排螺栓在外拉力的作用下,在翼缘根部和螺栓孔位置处出现了屈服.同时,由于单向螺栓套筒与孔壁间的滑移,使得端板与柱壁并非紧密贴合,所以撬力效应并不明显.因此对于内排螺栓应采用不考虑撬力影响的破坏模式1.
当各螺栓排之间没有设加劲肋时,螺栓排之间通常距离较近,这使得简化成螺栓群计算出的T形件有效长度比简化成单独螺栓排计算出的值要小.在这种情况下,为使得螺栓排受拉所提供的抗弯承载力最大化,对leff,i进行如下的修正[11],如表6所示.
结合表5和表6得到T形连接件翼缘受弯塑性
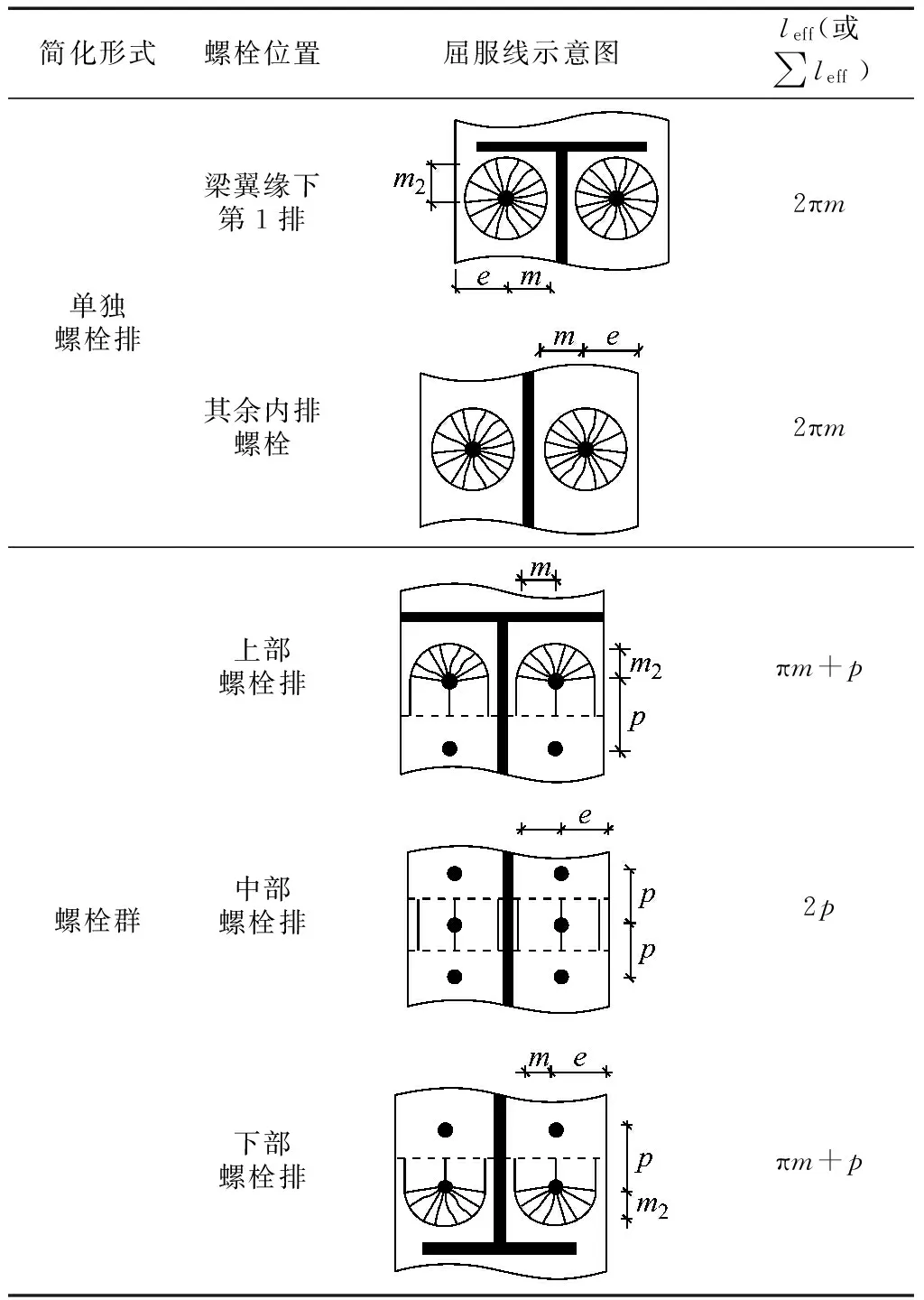
表5 T形连接翼缘受弯塑性铰线的有效长度Tab.5 Effective lengths for equivalent T-stubs

表6 各螺栓排受弯塑性铰线的有效长度修正Tab.6 Effective lengths for equivalent T-stubs
注:leff,i代表第i排螺栓单独简化成T形件时的有效长度;leff,i+j+k代表将第i,j,k排螺栓群简化成T形件时的有效长度.
铰线的有效长度后,根据表4可得到节点受弯时平齐端板上各螺栓排的受拉承载力.将其乘以对应的力臂后相加,则可以得到整个节点在端板强度控制下的抗弯承载力,即
Mep=∑FT,1,Rdhi
(2)
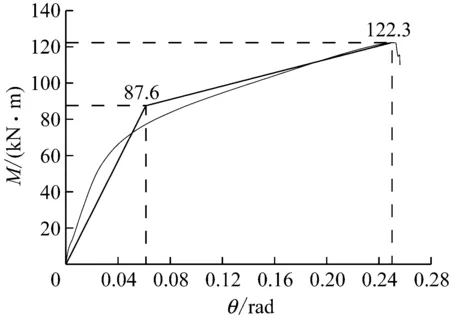
由于试验得到的M-θ曲线的屈服点不明显,故将M-θ曲线拟合为双直线,得到名义屈服点,见图13,并将其与计算得到的理论值进行对比,结果见表7.
a SR2-1试件

b SR2-2试件图13 双直线法处理试验数据Fig.13 Test data handled by double line method
对比理论计算值与试验结果可以发现,利用等效T形件法所求到的端板控制下的节点承载力跟试验吻合较好,误差在5%以内.
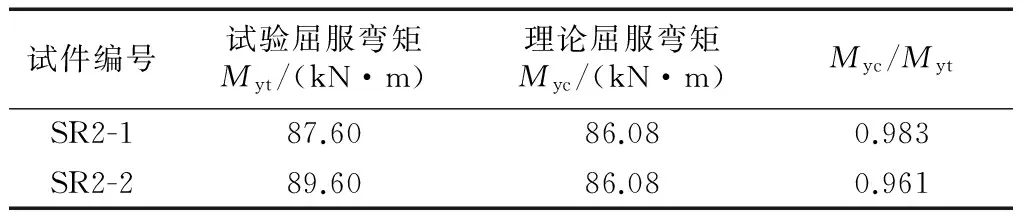
表7 SR2-1、2-2试件抗弯承载力理论值与试验值比较Tab.7 Comparison of moment resistancebetween theory and test results
3.3 柱壁强度控制的节点承载力计算
H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点在柱壁强度控制下的节点承载力计算可采用屈服线理论.屈服线理论是由Ingerslev首创,并由Johansen进行了广泛推广和改进,其基本原理是通过试验和理论分析假定一种与边界条件相协调的破坏机构,运用虚功原理或平衡方程确定极限荷载[4].当柱壁较弱时,柱壁的塑性发展准则很大程度上取决于端板相对于钢管柱的宽度[12].对于试件SR3-1和SR3-2,柱壁的厚度相对端板较薄,刚度较弱,同时端板的宽度又小于钢管柱的宽度,这样在弯矩作用下,节点受拉外凸的区域集中在最外两排螺栓处,受压内凹的区域集中在梁下翼缘处,如图8e和图8f所示.结合试验现象,对于平齐式端板单向螺栓连接节点,本文提出如图14所示的矩形钢管柱壁屈服线模式.
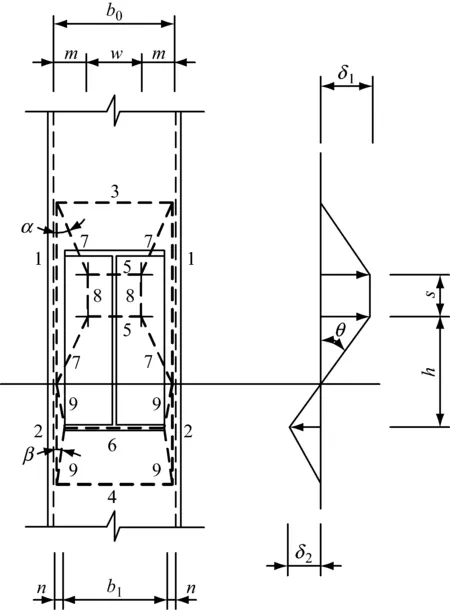
图14 屈服线模式Fig.14 Yield line model
根据虚功原理,即外弯矩M对于转角θ所做的外力功与具有塑性铰线长度li和转角φi的塑性铰系统的内能应相等,即
Mcfθ=∑liφiUL
(3)
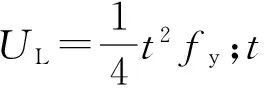
采用如图15所示的计算参数,屈服线1—9耗散的能量为
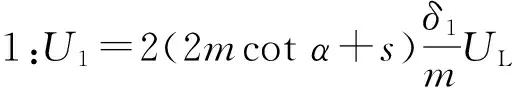
(4)
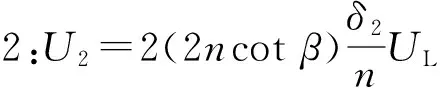
(5)

(6)

(7)
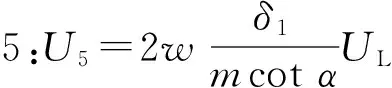
(8)

(9)
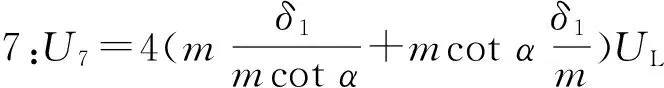
(10)
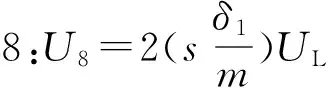
(11)

(12)
(13)
利用总势能驻值原理,对U求极值,有

(14)
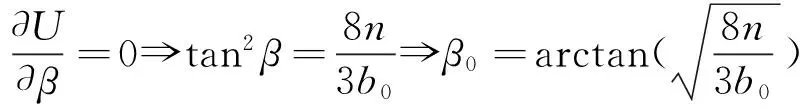
(15)
当单向螺栓连接节点的破坏模式由柱壁强度控制时,可将钢梁上下翼缘间的端板视为刚性板,补充连续性条件如下:
(16)
将式(4)—式(13)、式(16)代入式(3),可得
(17)
式中:α0、β0分别为屈服线7、9与柱壁之间夹角,可由式(14)和式(15)确定;m、n、s、b0为几何参数,具体见图14.
将试验中的构件参数代入式(17),可以得到H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点在柱壁强度控制下的抗弯承载力.对于矩形钢管柱,柱壁较容易发生弯曲变形,当钢管柱表面变形达到0.03b0,即柱宽度的3%时,视为节点达到极限承载能力[13].节点抗弯承载力试验值与理论计算结果对比见表8.

表8 SR3-1、SR3-2试件抗弯承载力理论值与试验值比较Tab.8 Comparison of moment resistance betweentheory and test results
由表8可知,由屈服线理论计算出的柱壁强度控制下的节点抗弯承载力与试验值接近,偏于保守.
4 结论
通过对H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点进行试验与理论分析,可得出以下结论:
(1)承受弯矩的H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点存在3种破坏模式:单向螺栓拉断、H型钢端板屈服塑性破坏以及柱壁屈服塑性破坏.
(2)提出了螺栓破坏模式下该种节点在弯矩作用下螺栓力的分布模式,即转动中性轴位于钢梁受压翼缘中心处,且忽略受压翼缘内排螺栓的贡献,而其余螺栓力按现行分布,并给出了抗弯承载力的理论计算公式.通过将理论计算值与试验值进行对比可知,两者吻合较好.
(3)在端板破坏模式下,利用EC3的等效T形件法,提出了端板强度控制的抗弯承载力理论计算公式,利用试验得到的弯矩-转角曲线,采用双直线法.得出屈服弯矩试验值.将理论值与试验值进行对比可知,两者吻合较好.
(4)在柱壁破坏模式下,利用屈服线理论,提出了该种节点在弯矩作用下的屈服线模式.基于虚功原理,建立了屈服线耗能和外荷载势能的关系,再利用总势能驻值原理,得出了该种破坏模式下的屈服弯矩理论计算公式,将理论计算值与试验值对比可知,两者数值较为接近,理论值偏于保守.
(5)对于H型钢梁与矩形钢管柱平齐式端板单向螺栓连接节点,螺栓破坏时接近脆性破坏,而柱壁屈服使得节点的变形过大,故端板屈服这种破坏机制是被鼓励的,所以在进行节点设计时,应避免发生螺栓破坏和柱壁屈服的情况,即建议设计时采用螺栓、柱壁强度控制下的节点承载力大于端板强度控制的节点承载力的原则.
(6)文献[4]介绍了H型钢梁与矩形钢管柱外伸式端板单向螺栓连接节点承载力的试验研究和理论计算公式,本文研究表明:在弯矩作用下,平齐式连接节点和外伸式连接节点类似,也存在3种破坏模式.通过对两种节点静力性能的比较可知:当梁柱构件尺寸和材料相同时,平齐式连接节点的承载力比外伸式连接节点低30%左右,但前者的转动能力比后者高25%左右.故平齐式端板连接节点的承载力较低,但延性较好,抗震性能较外伸式连接节点更好.
参考文献:
[1] 李国强, 石文龙, 王静峰. 半刚性连接钢框架结构设计[M]. 北京:中国建筑工业出版社, 2009.
LI Guoqiang, SHI Wenlong, WANG Jingfeng. Design of steel frames semi-rigid connections [M]. Beijing: China Architecture & Building Press, 2009.
[2] WANG Jingfeng, HAN Linhai, BRIAN U. Hysteretic behaviour of flush end plate joints to concrete-filled steel tubular columns [J]. Journal of Constructional Steel Research, 2009, 65(8): 1644.
[3] 许炎彬, 李国强, 张龙.单边紧固螺栓: 中国, 201210435247.7 [P]. 2012-11-5.
XU Yanbin,LI Guoqiang,ZHANG Long. One-way fastening bolt: China, 201210435247.7 [P].2012-11-05.
[4] 李国强, 段炼, 陆烨,等. H型钢梁与矩形钢管柱外伸式端板单向螺栓连接节点承载力试验与理论研究[J]. 建筑结构学报, 2015, 36(9):91.
LI Guoqiang, DUAN Lian, LU Ye,etal. Experimental and theoretical study of bearing capacity for extended end-plated connections between rectangular tubular columns and H-shaped beams with single direction bolts [J]. Journal of Building Structures, 2015, 36(9):91.
[5] 楼国彪, 李国强, 雷青. 钢结构高强度螺栓端板连接研究现状(Ⅰ)[J]. 建筑钢结构进展, 2006, 8(2):16.
LOU Guobiao, LI Guoqiang, LEI Qing. Recent developments in the behavior and design of high-strength bolted endplate connections [J]. Progress in Steel Building Structures, 2006, 8(2): 16.
[6] 中华人民共和国住房和城乡建设部,钢结构高强度螺栓连接技术规程:JGJ82—2011[S]. 北京:中国建筑工业出版社,2011.
Ministry of Housing and Urban-Rural Development of the People's Republic of China, Technical specification for high strength bolt connections of steel structures:JGJ82—2011[S]. Beijing: China Architecture & Building Press, 2011.
[7] 王燕. 钢结构半刚性连接设计理论及其工程应用[M]. 北京:中国建筑工业出版社, 2011.
WANG Yan. Design theory and application of semi-rigid connections of steel structure [M].Beijing: China Architecture & Building Press, 2011.
[8] British Standard Institution(BSI). Structural use of steelwork in building: BS5950[S]. London: BSI, 1994.
[9] American Institute of Steel Construction(AISC). Specification for structural steel buildings[S]. Chicago: AISC, 2010.
[10] European Committee for Standardization (CEN). EN 1993-1-8-Eurocode 3: design of steel structures -Part 1-8: design of joints[S]. Brussels: CEN, 2005
[11] BROWN D G, LLES D C. Joints in steel construction: moment-resisting joints to Eurocode 3[M]. London: The Steel Construction Institute, The British Constructional Steelwork Association Ltd., 2013.
[12] KUROBANE Y, PACKER J A, WARDENIER J, et al. Design guide for structural hollow section column connections[M]. Köln: TÜV-Verlag GmbH, 2004.
[13] CAO J, PACKER J, KOSTESKI N. Design guidelines for longitudinal plate to HSS connections[J]. Journal of Structural Engineering, 1998, 124(7): 784.

