有线通信浮标光纤线团受力分析及仿真
赵金才, 汤伟江, 孙铁绳
(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)
有线通信浮标光纤线团受力分析及仿真
赵金才,汤伟江,孙铁绳
(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)
针对采用轻质材料的有线通信浮标线团在制导光缆绕制成型中容易发生端板受挤压变形的问题, 结合有线通信浮标线团的结构特性及光纤线团绕制工艺, 对有线通信浮标线团端板和壳体在绕制中受力及变形情况进行分析, 通过板壳力学理论分析给出了端板变形的平衡微分方程、几何方程和物理方程。并根据实际边界条件和轻质材料特性对变形情况进行了仿真, 分析结果确定了影响端板变形的主要因素, 可为有线通信浮标线团设计提供参考。
有限通信浮标; 光纤线团; 轻质材料; 绕制工艺; 受力分析; 变形; 板壳力学
0 引言
浮标线团是有线通信浮标的重要组成部分,采用制导光缆绕制的通信浮标线团可搭载于水下航行体并与之实现宽频带、长距离实时信息交互,提高其作战效能[1]。有线通信浮标线团在自动化绕制设备上绕制, 在绕制张力等因素影响下将对浮标线团端板产生挤压作用使其发生弹性变形,对弹性模量较小的轻质材料而言这种变形尤为明显, 甚至直接影响线团壳体的装配和线包结构的稳定性。对该类变形通常的分析方法是运用薄壳变形的投影几何法和微分几何法, 并通过引入张量理论简化后从几何的角度确定格林应变非线性项的取舍, 但这类方法不易预测误差[2-3]。文中在建立合理的变形假设前提下, 采用板壳力学圆形端板的轴对称弯曲理论建立了端板变形的平衡微分方程、几何方程和物理方程, 结合绕制中边界条件, 对变形情况进行求解并代入相关轻质材料数据对变形进行了仿真和分析。从而确定了影响端板变形的主要因素, 仿真结果对通信浮标线团设计具有参考价值。
1 浮标线团结构与受力分析
1.1结构
浮标线团主要由端板、壳体、绕线轴、轴套及绕制好的线包组成, 如图1所示。

图1 浮标线团结构示意图Fig.1 Schematic of buoy clew structure
其中作为通信载体的制导光缆在一定绕制张力作用下沿绕线轴一匝匝紧密缠绕, 在端板处换向并跨匝至上一层继续绕制, 如此往复直至绕制设定长度或绕满整个端板, 最终形成通信线包。
1.2端板受力分析
在绕制张力下, 制导光缆在端板换向处每隔一层将对端板形成近似环形的均匀线载荷。这种线载荷随着层数的递增逐层施加在端板上, 由于制导光缆线经极细, 其作用在端板上的环形线载荷间距极小, 可近似认为端板承受均布载荷的作用。
如图 2所示, 以端板变形前中面的圆心为坐标原点, h为端板厚度, z为通过圆心且垂直于中面的对称轴方向坐标, r为中面上的点距z轴的距离, θ为极角建立圆柱坐标系进行分析。同时做以下基本假设。

图2 圆形板示意图Fig. 2 Schematic of circular plate
1) 端板中面法线变形后仍保持直线并垂直于变形后中面, 即不计横向剪切变形和中面法线的拉伸或压缩变形。
2) 平行于端板中面的所有面上的法向应力远小于其他应力分量, 可忽略不计。
3) 假设板的中面没有变形。
设端板单位面积上的横向载荷为q, 根据假设 1)、2), 从静力学方面可推导端板内力与载荷之间的关系[4], 即圆盘轴对称弯曲问题的平衡微分方程
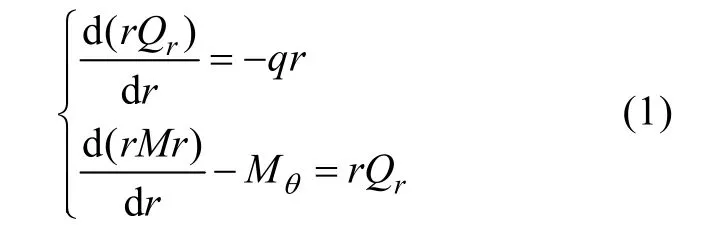
式中: Mr为径向弯矩;Mθ为环向弯矩;Qr为横向力。
在柱坐标下, 对于轴对称的端板内任一点的应变状态将由径向应变εr和环向应变εθ决定。根据假设 3), 端板中面上任一点没有面内的位移,仅有垂直方向的位移, 即为挠度ω, 把变形后端板的中曲面称为挠度曲面, 可得端板在轴对称变形情况下应变与位移关系几何方程组

此外, 应用虎克定律, 可得圆板在轴对称变化情况下的物理方程, 应用几何方程并代入薄板的内力计算公式, 可得物理方程的最终形式

式中, D为抗弯强度, 代表圆板抵抗弯曲的一种性能, 对于圆形板, ν为材料的泊松比, E为杨氏模量。
根据方程组(1)、(2)、(3), 选择挠度ω为独立变量, 将上述 6个方程进行消减, 最后求出1个仅含挠度的单一微分方程
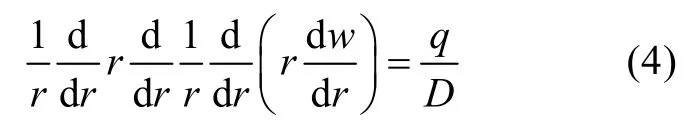
解此方程可得圆板在不同位置处的变形量,以q为均布载荷q0为例,上式的通解为
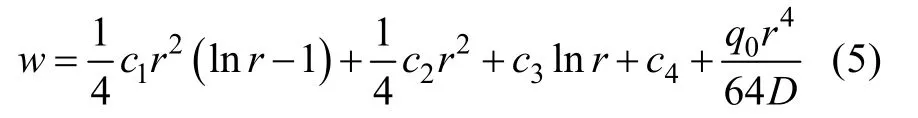
式中,c1,c2,c3和c4为积分常数。
根据浮标线团的端板结构, 设a为外径、b为内径, 又根据端板的安装结构可视为内边缘固定、外边缘自由, 如图3所示。

图3 端板受力示意图Fig. 3 Force analysis on end plate
由边界条件可知:当rb=时, 挠度和转角都必须为0, 即

当ra=时, 弯矩和有效横向力为0, 即

将式(5)代入式(6)、式(7)可得关于积分常数c1~c4四元代数方程组

可见, 当q0, D, ν, b和a已知后即得积分常数q1c,c2,c3和 c4,从而可解出挠度随半径的变化关系。
1.3端板受力计算
如图4所示, 设绕线轴半径为R0,绕制张力为T, 以绕制n层制导光缆为例, 设最内层为第1层, 对应绕制半径为R1,依次向外最外层为第n层,半径为Rn。

图4 制导光缆线团绕制受力示意图Fig. 4 Schematic forces in guidance optical cable winding
因绕制中后层制导光缆会对前层进行包绕从而使前层已绕的制导光缆张力减小, 且这种张力减小的程度与该层所在的位置有关。设制导光缆对线轴的垂直力为Pver,对端板的水平力为Phor,则第i层制导光缆作用于绕线轴的垂直力[5-6]
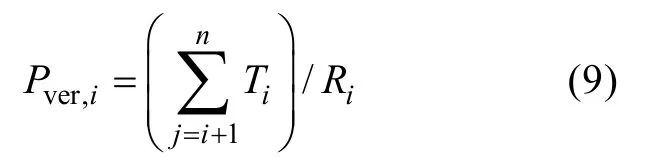
式中: Ri为第i层制导光缆到绕线轴中心的缠绕半径;Ti为i层制导光缆的张力, 考虑到制导光缆由于其上面一层缠绕而产生的压力卸载, 取拉力与层数之间的关系为。由图4可知,第i层制导光缆作用于绕线轴的水平力, 由于制导光缆各匝层紧密缠绕, 于是30α=°, 故对于绕制n层制导光缆, 则制导光缆对端板总的合力为

考虑到制导光缆绕制时每隔一层的第1匝制导光缆将和端板紧密接触并通过绕制张力作用对端板形成近似的环形横向力, 若将各圈环形横向力视为均匀载荷, 结合图3环形载荷的内、外径和式(10)端板所受总合力, 则端板所受的均布载荷可表示为
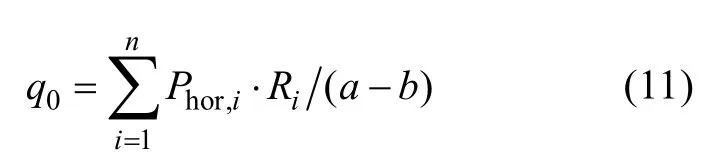
1.4壳体受力分析
根据浮标线团的结构形式, 其壳体通过螺钉与端板周向连接固定, 壳体的受力分别通过与端板垂直连接及与端板径向连接的螺钉实现, 因为与端板垂直连接的壳体部分相对于壳体的长度较小, 整个壳体的受力情况可简化为图5所示。
新西兰驻广州总领事Rachel Maidment CG女士也表示:“金樽奖是真正有影响力的活动,它为推动中国独特而又蓬勃的葡萄酒市场发挥着主要作用。”Rachel Maidment CG女士对新西兰葡萄酒在中国市场带有极高的信任和期望,她谈到:“我们生产仅不到全球1%的葡萄酒,并且我们特意关注质量而非数量。新西兰98%的葡萄酒庄都被认证为可持续发展的,只有经过注册成为可持续发展的葡萄酒才有资格被列入新西兰葡萄酒酿造协会的全球活动中。所以我们可以保证我们在全球市场踏出最佳前进的步伐。”

图5 壳体受力示意图Fig. 5 Force analysis on shell
不考虑壳体表面的开孔所引起的应力集中且假定两端均布各螺钉的受力均匀, 按壳体所受应力及应变的关系计算。其中: S为壳体的横截面积, d为壳体厚度, x为壳体内径, 近似计算时可取xa=(a为端板外经), F为壳体截面内的总载荷。
可见, 应力与应变成正比且当壳体横截面积一定时, 应力会随着载荷F的增加而增大, 对于某一种材料, 应力的增长是有限度的, 超过这一限度, 材料就要破环, 从而使结构出现失稳, 此时的最大应力值即为给定材料的最大许用应力[7]。
通过上述分析可见, 为保证壳体结构的稳定性, 可令壳体的最大轴向变形量ε等于端板最外沿的挠度值ω, 此时应力σ最大, 通过S值即可计算作用在壳体上的载荷F。
2 仿真结果与分析
2.1浮标线团端板受力仿真
当给定内外径和绕制层数后, 可计算端板的均布载荷q0。结合绕制工艺和绕满整个线包的实际要求, 其外径又由绕制层数决定, 据此可将式(11)改写为

以T=Fc为例可得载荷与层数的关系如图 6所示。
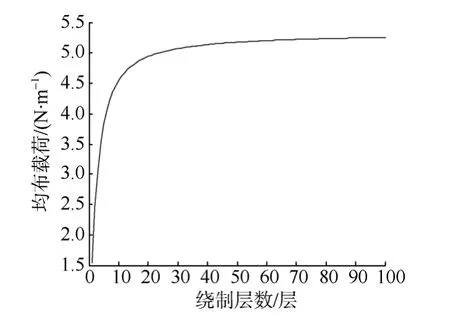
图6 端板均布载荷与绕制层数变化曲线Fig. 6 Curve of uniform load on end plate versus winding tier
2.2浮标线团端板变形仿真
ABS材料以接近于水的密度和较高的机械强度、较强的环境适应性等因素成为通信浮标线团的理想轻质材料选择。其主要指标如下[8-9]: 密度1.02 g/mm3; 模量2 000 N/mm2; 0.39, 强度30 N/mm2。结合式(8)可得, 挠度沿端板半径方向的变化关系曲线。以绕制 50层为例, 由图 6得q0≈5.18N/m, 假定绕线轴径D0=100, 端板外径D≈135mm, 可得图7所示的仿真曲线。
图7给出了在环形端板上绕满50层线导制导光缆后端板不同位置处的挠度值。可见环形端板在均布载荷下沿半径方向其变形量逐渐增大且最大变形量发生在端板最外沿处。这是因为绕制中端板内端由刚体材料的工装夹具固定, 轴向变形空间有限, 而端板因外端自由, 故随着表面横向总载荷的增大其变形量会逐渐加大。若忽略工装夹具对端板内端的影响, 则绕制 50层制导光缆时单侧端板的最大变形量约为0.15 mm。
为进一步分析不同绕制层数和端板尺寸下的变形情况, 可在设定绕制张力下依式(8)和相关参数, 绘制不同绕制层数下对应端板最外沿的挠度值, 如图 8所示, 即为绕制不同层数的线团单侧端板所产生的最大变形量。

图7 指定端板后挠度随半径方向的变化曲线Fig. 7 Curve of deflection versus radius direction for a certain end plate
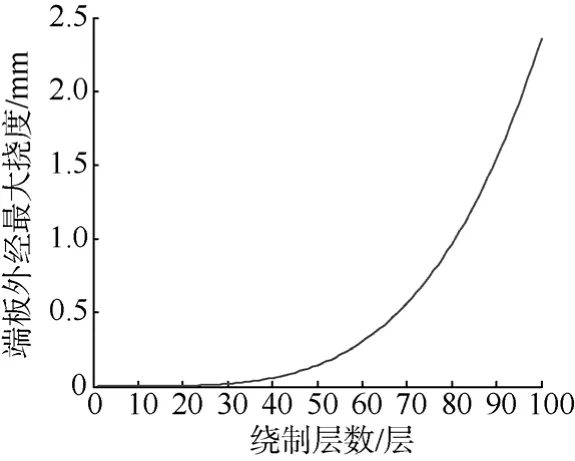
图8 不同绕制层数对应端板外径的最大挠度Fig. 8 Curve of the maximum deflection at outer diameter of end plate versus winding tier
由图 8可见, 对于给定的参数值, 当绕制层数小于 30时, 端板的最大变形量较小可忽略不计; 但绕制层数再进一步增大后, 端板的最大变形量快速升高, 当层数绕制 100层制导光缆线团时, 单侧端板的最大变形量约为2.3 mm, 即出现显著变形。这就要求在其他参数不可改变时, 针对浮标线团设计应尽量减小绕制层数以降低两端板之间的变形量。下面根据端板之间的变形量,分析不使浮标线团壳体结构失稳所能承受的两端板之间的最大变形量。
2.3浮标线团壳体变形仿真
通过求解对应层数下的端板最大挠度值ωmax,可解算出壳体在端板最大间距下的应力σmax,通过与 ABS材料拉伸强度值进行比较后,可得在线团壳体不被破环的情况下所需的厚度y;结合端板变形仿真结果可对不同壳体厚度下的拉力进行仿真计算, 如图9所示。
图9给出了对应不同壳体厚度时所需的拉力值, 从图中可见, 随着壳体厚度的增大, 在许用应力下所需的拉力也逐渐增加。

图9 不同壳体厚度对应的拉力值Fig. 9 Curve of pulling force versus shell thickness
3不同参数仿真对比
分析上述仿真结果可知, 浮标线团单侧端板的变形量主要与绕制层数和该层数所确定的端板外径以及内径值有关。在材料确定后变形程度还与端板的厚度有关。此外, 实际中壳体与端板通过螺钉连接, 在连接处将产生应力集中, 使壳体结构失稳的应力值可能远小于仿真中的许用力值。因此在壳体设计时可在壳体长度与端板间预留一定的间隙以适应端板变形后的装配。
综上通信浮标线团的结构分析可转化为端板在不同参数下绕制不同层数的变形量分析。下面通过给定不同端板厚度和内径对绕制不同层数下的单侧端板变形量进行仿真, 分别如图10、图11所示[10]。当假设绕制张力T=Fc,端板内径b=50mm时, 不同的h值下最大挠度随层数的变化关系曲线见图10。当假设绕制张力为T=Fc,端板厚度h=15 mm时,不同的b值下最大挠度随层数的变化关系曲线见图11。

图10 不同端板厚度下最大挠度随层数变化曲线Fig. 10 Curves of the maximum deflection versus winding tier for different end plate thickness
由图10可见, 端板厚度对其挠度变化影响较大且随着厚度的增加端板的最大挠度快速减小,当厚度为18 mm时, 即使绕制100层线导光缆其单侧端板的变形量也小于1 mm。图11显示, 端板内径即使增加一倍, 对缠绕相同层数的光缆其端板变形量几乎没有改变。因此相比于线团端板的内径,端板厚度对绕制端板的变形量影响更为显著。
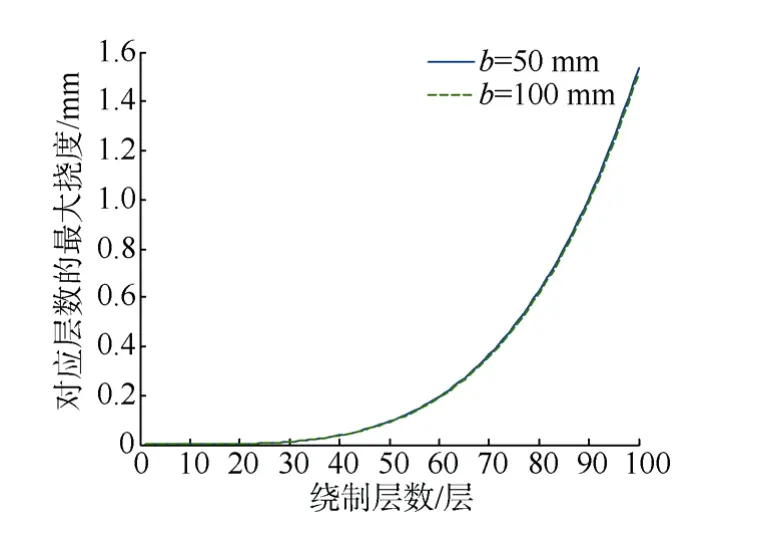
图11 不同端板内径下最大挠度随层数变化曲线Fig. 11 Curves of the maximum deflection versus winding tier for different inner diameter of end plate
同理, 当固定端板厚度 h=15 mm, 内径 b= 50 mm时, 通过改变绕制张力T可得如图12所示仿真曲线。

图12 不同绕制张力下最大挠度随层数变化曲线Fig. 12 Curves of the maximum deflection versus winding tier under different tensile force
可见, 张力对端板变形量的影响也较大且随着绕制力值的增大变形量也快速增大。故在不影响线团成型的前提下, 可适当降低绕制工艺中的张力从而进一步降低端板的变形量。
通过前述分析可知, 为使绕制制导光缆线团端的变间距离尽可能小, 可通过减小绕制张力和提高端板厚度的方式来实现。从图10和图12可见, 当绕线层数小于50层时, 即使改变相关参数,端板的变形量均较小, 两端板间的总变形量小于0.5 mm, 这种小变形完全可以通过设计装配误差来弥补。
4 结束语
文中结合制导光缆线团的绕制工艺对有线通信浮标用制导光缆线团的端板和壳体受力情况进行了理论分析与推导, 并以 ABS轻质材料特性参数为例对浮标线团的变形情况进行了仿真计算。仿真结果表明, 端板厚度和绕制张力是影响线团变形的主要影响因素。为简化计算, 文中将当前绕制张力对已绕各层的压力卸载进行了假定, 实际中压力变化受张力、绕制半径、制导光缆材料特性等多种因素影响, 其精确计算有待进一步研究。
[1] 李建辰. 鱼雷定位技术[M]. 北京: 国防工业出版社,2009.
[2] 董文堂, 李卓球. 基于一种简化Green应变的薄壳大挠度方程[J]. 固体力学学报, 2005, 26(3): 347-350. Dong Wen-tang, Li Zhuo-qiu. Large Deflection Equations of Thin Shells Based on the Simplified Green Strain[J]. Acta Mechanica Solida Sinica, 2005, 26(3): 347-350.
[3] Li M, Zhan F. The Finite Deformation Theory for Beam,Plate and Shell Part IV[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 182(1-2): 187-203.
[4] 刘怀人. 板壳力学[M]. 北京: 机械工业出版社, 1990.
[5] 严兵, 姚海. 浮式起重机篱笆式卷筒的结构强度及稳定性分析[J]. 船舶工程, 2012, (z2): 204-205. Yan Bing, Yao Hai. Study on Strength and Stability of Le-Bus Grooved Drum Applied in Offshore Crane[J]. Ship Engineering, 2012, (z2): 204-205.
[6] 但斌斌, 周鼎, 王光青. 钢丝绳缠绕卷筒的计算原理及其应用[J]. 湖北工学院学报, 2003, 18(2): 75-76. Dan Bin-bin, Zhou Ding. The Calculation Principle of Steel Rope Twining Reel[J]. Journal of Hubei Polytechnic University, 2003, 18(2): 75-76.
[7] 陈传尧. 工程力学基础[M]. 武汉: 华中科技大学出版社, 1999.
[8] ABS. EWZ-001-02-P03-W015 Deck Machinery Attachment A[S]. USA: ABS, 2008.
[9] 赵启辉. 常用非金属材料手册[M]. 北京: 中国标准出版社, 2008.
[10] 陈杰. Matlab宝典[M]第四版. 北京: 电子工业出版社,2013.
(责任编辑: 许妍)
Force Analysis and Simulation of Optical Fiber Clew for Wired Communication Buoy
ZHAO Jin-cai,TANG Wei-jiang,SUN Tie-sheng
(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China)
To solve the end plate extrusion deformation problem of the wired communication buoy′s optical fiber clew,which is made from lightweight material, in the winding process of guidance optical cable, this paper analyzes the force and deformation of the end plate and shell by considering the structure features and winding process of the optical fiber clew, and employs the theory of plate and shell mechanics to derive the balanced differential equation, geometric equation and physical equation of the end plate deformation. Moreover, a simulation of the end plate deformation is conducted according to real boundary condition and the characteristics of the lightweight material, and the main factors affecting the end plate deformation are determined. The research is of benefit to the design of the wired communication buoy′s optical fiber clew.
wired communication buoy; optical fiber clew; lightweight material; winding process; force analysis; deformation; plate and shell mechanics
TJ630; O39
A
1673-1948(2016)05-0384-06
10.11993/j.issn.1673-1948.2016.05.013
2016-06-28;
2016-08-11.
赵金才(1982-), 男, 硕士, 工程师, 主要研究方向为鱼雷线导技术.

