弹射式水下航行器发射装置发射筒内径对内弹道的影响

马　辉

（中国船舶重工集团公司 第726研究所， 上海， 201108）

弹射式水下航行器发射装置发射筒内径对内弹道的影响

马辉

（中国船舶重工集团公司 第726研究所， 上海， 201108）

为兼顾水下航行器发射装置发射效率与装置尺寸， 应设计合理的发射筒内径。文中基于多对多交界面技术， 解决了带孔壁面间无间隙滑移的仿真难题， 建立了耦合求解非定常流场和航行器、活塞运动的数值仿真模型。通过在Fluent软件中的二次开发实现了弹射式水下航行器发射内弹道仿真， 并对不同发射筒内径的发射装置计算流场以及运动时历曲线进行分析。仿真结果表明， 水下航行器发射装置发射筒内径在一定范围内对发射效率影响呈显著正相关， 随着发射筒内径增加， 其影响逐渐减弱， 且出筒效率趋于稳定。基于多对多交界面技术的水下航行器发射仿真是可靠的， 可为弹射式水下发射装置设计提供参考。

水下航行器发射装置； 弹射式； 内弹道； 多对多交界面技术

0　引言

水下航行器发射的动力式发射装置主要分为涡轮泵式和弹射式［1］。其中， 涡轮泵式发射装置［2-4］已有较多研究， 而弹射式发射装置［5-6］的研究较少。弹射式发射装置具有蓄能快、发射周期短、发射噪音小的优点， 因此在对航行器出筒速度要求不高的场合具有很大的应用价值。采用弹簧动力源的弹射式发射装置通常采用开放式储能筒结构， 由于发射筒壁与航行器的间隙大小对筒内补水效果具有较大影响， 因此， 合理设计发射筒内径， 成为了影响出筒效率的关键因素之一。

在水下航行器发射的内弹道仿真方面， 国内外学者已开展了多项研究。对于不需要考虑流场细节的发射系统， 通常对发射装置各环节采用理论或实验的方法， 确定各环节的传递函数， 进而在MATLAB/Simulink环境下进行了仿真［7-8］。在水下航行器发射过程中， 通常弹体周围的流场对弹体的作用力是弹体受力的主要成分， 不宜简化处理， 而须采用计算流体力学（computational fluid dynamics， CFD）方法对流场加以精确计算。张孝芳［9］等采用CFD方法对液压平衡式发射装置中活塞的缓冲特性进行了研究， 但处理仅局限于2D， 且未考虑活塞与流体的耦合作用。

文中针对采用弹簧动力源的弹射式水下航行器发射装置， 采用多对多的交界面技术解决了活塞、航行器以及筒壁间小间隙相对运动的难点，在Fluent软件［10］的UDF中二次开发来控制活塞、航行器的耦合运动， 实现了内弹道的数值仿真，获得了发射筒内径对内弹道的影响， 为弹射式水下航行器发射装置设计提供参考。

1　发射装置建模

1.1建模优化

1） 物理模型

弹射式水下航行器发射装置由上发射筒、活塞、弹簧、导轨组成。弹簧位于活塞正下方下处于预紧状态， 航行器与导轨平行且垂直支撑于活塞上； 航行器发射时， 控制活塞的开关松开， 弹簧推动活塞以及航行器向上加速运动， 活塞推送一定距离后与航行器分离， 航行器继续向上运动至出筒。水下航行器发射装置如图1所示。

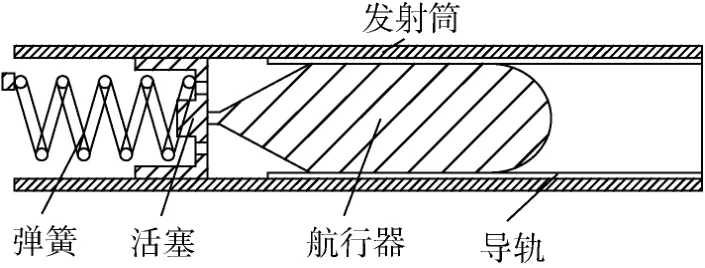
图1　水下航行器发射装置结构简图Fig. 1　Structure of an underwater vehicle launcher

针对水下航行器发射装置的特征， 做出相应简化如下: a. 考虑计算模型的对称性， 采用 1/4建模， 节约计算成本； b. 在航行器与活塞之间人为增加6 mm的小间隙， 保证航行器与活塞之间的网格一直存在， 使计算顺利进行； c. 忽略弹簧以及导轨的体积； d. 由于模型中存在一些固有的小间隙通常以润滑剂填充， 假定当间隙小于1 mm时，直接忽略该间隙， 假设物面重合并忽略摩擦力； e.忽略发射筒壁的厚度， 并按内径大小建模。

2） 流体流动模型

对于文中研究水下航行器发射过程， 由于弹体发射并未出水， 因此， 可以采用不可压的单相流计算模型进行计算。另外， 由于管内的流动雷诺数大约为 106量级， 管内流体处于湍流状态，须采用湍流模型处理流体脉动速度。在张量记法下， 这里给出相应的流场控制方程

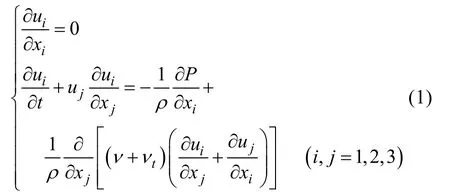
式中: u为流体速度；ν为流体粘度；ρ为流体密度；νt为涡粘滞系数， 取决于流动状态； P定义为， κ为湍动能， p为流体压力。为使方程封闭， 采用κω-SST两方程模型。

3） 活塞及航行器力学模型

航行器水下弹射过程分为2个阶段。初始阶段活塞与航行器作为整体从零速度开始加速运动。受力方程如下

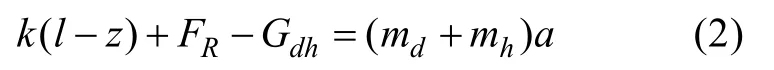
式中: k为弹簧的刚度系数； l为弹簧预压缩长度； z为航行器的位移； FR为流体作用于航行器与活塞上的总阻力； Gdh为航行器与活塞水中的总质量；md为航行器在空气中的质量； mh为活塞在空气中的质量； a为整体的加速度。

当运动至某一时刻， 活塞加速度小于航行器，即航行器的速度开始大于活塞， 发生分离， 进入第 2阶段。此时， 活塞与航行器单独运动， 而其相互影响则通过流体作用的总阻力体现。分离后，航行器与活塞受力方程如下

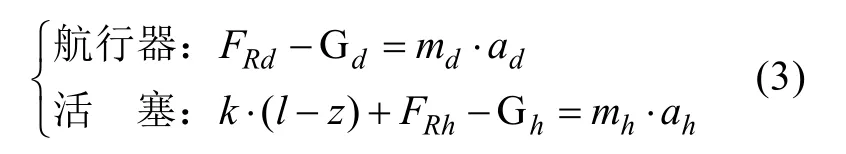
式中: FRd为航行器受流体的总阻力； FRh为活塞受水的总阻力； Gd为航行器水中的重力； Gh为活塞在水中的重力； ad为航行器的加速度； ah为活塞的加速度。

1.2计算区域及网格划分

依照前述假设， 计算坐标系以及选取计算区域如图2所示。计算坐标系中心选取在航行器末端， z轴沿航行器轴线向上。航行器前方选取约4倍航行器长度的距离， 周向选取约 0.5倍航行器长度的距离以保证边界截断影响可以忽略。

图2　计算流场区域示意图Fig. 2　Schematic of calculating flow field region

考虑到航行器与活塞均为单方向的运动， 这里仅采用层铺的动网格模式， 保证网格质量以及计算效率。由于发射装置中涉及到多个物体的相对运动， 必须进行多区域划分并采用多对多的交界面技术。区域划分如图3所示。

图3　流场区域划分示意图Fig. 3　Schematic of dividing flow field region

图3中数值标号处为设置的交界面， 其中1、2、3、6为多对多的交界面。在多对多的交界面设置下， 交界面有一边为壁面或未定义边界时则该部分边界作壁面处理， 在交界面两边均为流场内域时则作为交界面传递信息， 这使得活塞壁与带孔筒壁间的滑移处理十分简便。在多区域划分下的计算网格如图4所示。整个计算域网格数约70万， 并采用边界层网格对装置壁面加密， 经试算能保证较高的精度和计算效率。

图4　计算网格划分图Fig. 4　Meshing for calculation

2　发射装置内径研究

2.1研究模型选取

对于水下发射装置优化设计而言， 航行器的尺寸、航行器质量、弹簧的刚度、弹簧的预压缩量等通常是不可改变， 而可优化的参数主要在于发射装置的一些物理参数， 如发射筒内径、筒壁开孔面积、开孔位置、开孔形状以及活塞形状等，其中发射筒内径的大小作为影响筒内补水的主要因素， 必须优先加以研究。

为排除装置筒壁上开孔等因素影响， 这里采用底部全开， 而侧壁不开孔研究模型如图 5所示。由于发射的水下航行器主体最大直径为118 mm， 预期设计发射装置发射筒直径135 mm，考虑到实际设计范围， 这里选取 130 mm、135 mm、140 mm、145 mm和150 mm 5组发射筒内径作为研究对象， 同时设置 1组无筒壁的发射装置作为发射筒内径无穷大的极限设计参照。

图5　内径135 mm发射装置模型图Fig. 5　Launcher model with inner diameter of 135 mm

为研究发射装置发射筒内径对内弹道的影响，须保证装置其他参数尽量一致， 选取模型的其他参数见表 1。选取活塞物理尺寸一致， 减少活塞的影响， 同时选取发射装置底部全开以保证补水充足。

2.2数值仿真结果与分析

针对上述选取的发射装置， 对应的数值仿真速度场如图6所示。图6给出了0.06 s航行器与活塞分离后的 6组模型的速度场云图， 其中（a）D=130 mm； （b） D=135 mm； （c） D=140 mm； （d）D=145 mm； （e） D= 150 mm； （f） D=无穷。由速度场云图可见， 随着发射筒内径变小， 航行器尾部流体颜色加深， 即流体速度变大， 压力变小， 从而航行器前后压力差越大， 所受到的阻力也越大。这些流场特性与实际情况相符， 证明文中数值仿真结果是可靠的， 相应地给出速度与位移的时历曲线见图7。由图 7的速度曲线可见， 随着发射筒内径变小，航行器速度增加越慢， 而衰减却越快， 这表明航行器在加速以及减速运动 2个阶段所受的阻力均增加。由图8的位移曲线可见， 随着发射筒内径的减小， 出筒时间增加， 当发射筒内径减小至一定程度后， 出筒时间增加迅速， 甚至无法出筒。

表1　不同发射筒内径模型相同参数Table 1　The same parameters of models with different tube inner diameter model

图 6　t=0.06 s时不同内径发射装置速度云图Fig. 6　Velocity contour of launchers with different inner diameters when t=0.06 s

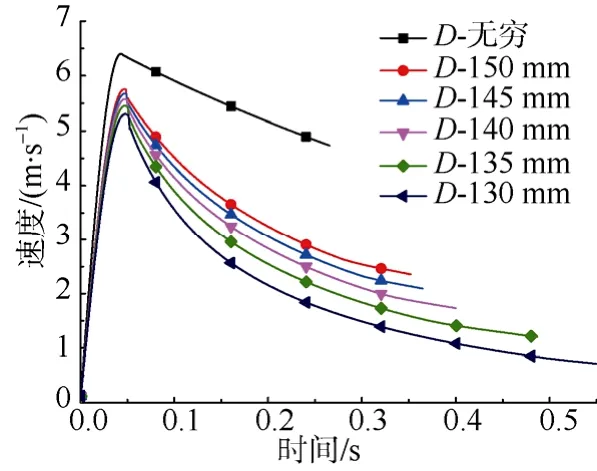
图7　不同发射筒内径模型速度曲线Fig. 7　Velocity-time curves of models with different tube′s inner diameters

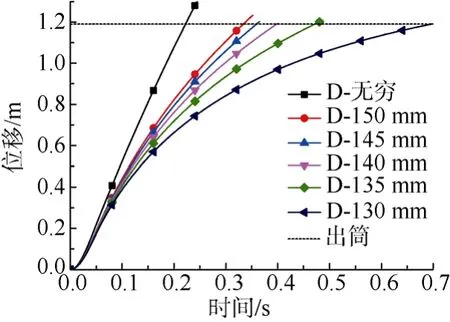
图8　不同发射筒内径模型位移曲线Fig. 8　Displacement-time curves of models with different tube′s inner diameters

表2给出了不同储能筒开孔模型下的出筒速度时间表。其中， 无因次的内径为发射筒内径 D与航行器主体最大直径Dm的比值。由表可见， 当发射筒内径为130 mm时， 增加5 m内径能将出筒速度提高145%， 而同样的内径增量在145 mm内径时航行器出筒效率仅能提高 14%， 可见发射筒内径的影响随着内径的增加而减弱。

由表2数据作图， 并将数据点采用B样条曲线拟合如图9所示。其中横坐标为无因次内径， 纵坐标为出筒效率。出筒时间与出筒速度均随无因次开孔直径约呈双曲型变化规律， 随着发射筒内径的增大， 出筒时间与出筒速度缓慢趋于稳定。

表2　不同发射筒内径模型计算出筒效率Table 2　Calculated out-tube efficiency of models with different tube′s inner diameters

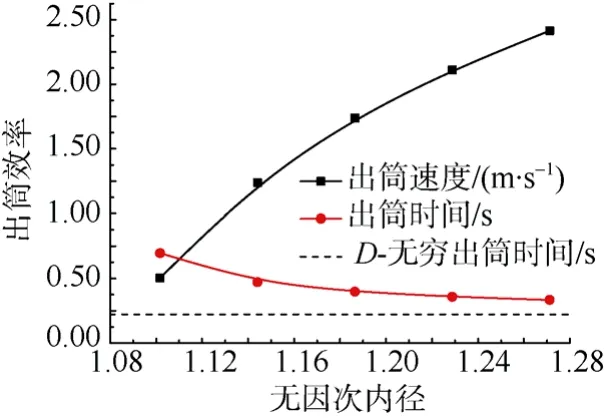
图9　不同发射筒内径模型出筒效率数据拟合图Fig. 9　Data fitting curves of out-tube efficiency of models with different tube inner diameters

3　结束语

文中针对水下航行器发射装置发射航行器出筒过程， 建模时考虑了流场中活塞与航行器的耦合作用， 使计算结果更为真实可信。同时采用了多对多的交界面技术， 仅需采用滑移以及层铺的动网格即可完成数值仿真， 保证了物体运动时网格的质量。另外， 对弹射式水下发射装置内径的影响进行了相应研究， 并将内径无因次化， 使结果具有普遍性， 为弹射式水下航行器发射装置的研究设计提供了参考。

文中在研究发射筒内径时， 仅考虑了活塞的几何尺寸不变， 并未对保证活塞端面透水面积或透水面积比例一定的情况下进行发射筒内径的研究。这些因素必然会使无因次内径对出筒效率的影响曲线产生变动， 因此， 相关因素变化后的影响仍然有待后续进一步探讨。

［1］ 朱清浩， 宋汝刚. 美国潜艇鱼雷发射装置使用方式初探［J］. 鱼雷技术， 2012， 20（3）: 215-219. Zhu Qing-hao， Song Ru-gang. Preliminary Exploration on Launch Modes of U.S. Submarine Torpedo Launchers［J］. Torpedo Technology， 2012， 20（3）: 215-219.

［2］ 魏勇， 逄洪照， 赵祚德. 水压平衡式鱼雷发射装置气缸活塞行程对鱼雷内弹道的影响［J］. 火力与指挥控制， 2013， 38（11）: 137-140. Wei Yong， Pang Hong-zhao， Zhao Zuo-de. Impact Research on Torpedo Internal Ballistic for Cylinder Piston Effective Stroke of Hydraulic Equalized Torpedo Launcher［J］. Fire Control&Command Control， 2013， 38（11）: 137-140.

［3］ 魏勇， 逄洪照. 基于蒙特卡洛法的发射管内弹道参数分布的研究［J］. 鱼雷技术， 2006， 14（1）: 31-34. Wei Yong， Pang Hong-zhao. In-tube Ballistic Parameters Distribution Based on Monte Carlo Method［J］. Torpedo Technology， 2006， 14（1）: 31-34.

［4］ 练永庆， 任德奎， 李宗吉， 等. 弹性发射水舱对潜艇鱼雷发射内弹道的影响［J］. 弹道学报， 2013， 25（1）: 77-80. Lian Yong-qing， Ren De-kui， Li Zong-ji， et al. Influence of Elastic Launching Tank on Interior Ballistics of Torpedo Launched from Submarine［J］. Journal of Ballistics，2013， 25（1）: 77-80.

［5］ 邹广宝. 活塞式垂直弹射系统内弹道性能研究［C］//中国宇航学会导弹航天器发射技术研讨会. 安徽: 中国宇航学会， 1998.

［6］ 谢伟， 王汉平. 提拉式弹射内弹道特性的影响因素分析［J］. 固体火箭技术， 2016， 39（1）: 146-150. Xie Wei， Wang Han-ping， Influential Factors Analysis on Interior Ballistic Performance of Lift-draw Ejecting Device［J］. Journal of Solid Rocket Technology， 2016， 39（1）: 146-150.

［7］ 田兵， 王树宗， 练永庆. 液压蓄能式鱼雷发射装置内弹道建模与仿真［J］. 鱼雷技术， 2011， 19（1）: 68-71. Tian Bing， Wang Shu-zong， Lian Yong-qing. Inner Trajectory Modeling and Simulation of Hydraulic Energy Accumulated Torpedo Launcher［J］. Torpedo Technology，2011， 19（1）: 68-71.

［8］ 胡柏顺， 穆连运， 赵祚德. 潜艇水压平衡式发射装置内弹道仿真建模［J］. 舰船科学技术， 2011， 33（7）: 90-93. Hu Bai-shun， Mu Lian-yun， Zhao Zuo-de. Simulation and Model of Submarine Hydraulic and Balanceable Launching Equipment Inside Trajectory［J］. Ship Science & Technology， 2011， 33（7）: 90-93

［9］ 张孝芳， 胡坤， 由文立. 液压平衡式水下鱼雷发射系统活塞缓冲特性数值仿真［J］. 兵工学报， 2011， 32（9）: 1089-1093. Zhang Xiao-fang， Hu Kun， You Wen-li. Numerical Simulation on Piston Buffering Characteristics of Pressure-balanced Underwater Torpedo Launch System［J］. Acta Armamentarii，2011， 32（9）: 1089-1093.

［10］ 丁源， 王清. ANSYS ICEM CFD 从入门到精通［M］. 清华大学出版社， 2013.

（责任编辑: 许妍）

Influence of Tube′s Inner Diameter on Interior Trajectory for Underwater Vehicle Ejection Launcher

MA Hui
（The 726 Research Institute， China Shipbuilding Industry Corporation， Shanghai 201108， China）

To balance launch efficiency and size of an underwater vehicle launcher and design proper inner diameter of the launching tube， the many-to-many interface scheme is adopt to overcome the simulation difficulty of gapless slipping between the walls with holes， and a simulation model for solving coupled unsteady flow field， piston and vehicle movement is built. Interior trajectory simulation with different tube′s inner diameters is accomplished by secondary development in software Fluent， and the calculated flow fields as well as the movement time history curve are analyzed. Simulation results reveal that the inner diameter of the tube shows obviously positive correlation with the launching efficiency within a certain scope， while the influence of the inner diameter gradually weakens as the inner diameter increases， and finally the out-tube efficiency tends to be stable. It is concluded that the simulation of underwater vehicle launcher based on many-to-many scheme is reliable， and may be applied to design of underwater vehicle ejection launcher.

underwater vehicle launcher； ejection mode； interior trajectory； many-to-many interface scheme

TJ 635； O315

A

1673-1948（2016）05-0396-05

10.11993/j.issn.1673-1948.2016.05.015

2016-07-28；

2016-08-25.

马 辉（1978-）， 女， 工程师， 主要从事水下总体技术及流体计算.