声学多普勒测流波形分析
张宇航, 杨云川 吕林夏 王海陆 岳 玲 李金明
(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制重点实验室, 陕西 西安,710077)
声学多普勒测流波形分析
张宇航1,2,杨云川1,吕林夏1,王海陆1,岳玲1,李金明1
(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制重点实验室, 陕西 西安,710077)
为了提高多普勒测流技术的测速精度和距离分辨力, 文中基于多普勒测流实际应用背景, 选取具有大时宽带宽乘积的 Costas频率编码信号和几种相位编码信号进行综合波形分析和比较, 研究发现二进制相移键控(BPSK)信号更有利于获得高的测速精度和距离分辨力, 且在低速条件下具有较好的抗混响能力。计算机仿真中采用复自相关算法估计多普勒频率的精度。结果表明, 在相同条件下发射BPSK信号测量得到的速度表征方差最小,更适用于高分辨多普勒流速测量。
多普勒测流; 波形分析; 二进制相移键控信号(BPSK); Costas频率编码
0 引言
声学多普勒流速剖面仪(acoustic Doppler current profiler, ADCP)是一种根据水声多普勒原理研制的新型测速声呐, 主要用来遥测较大范围内的海流速度。ADCP 既可用于舰船的定位导航,又广泛应用于海洋及内陆河流的测流领域。
在多普勒测流技术研究中, 发射信号形式的选择是首先要考虑的问题, 不同发射信号波形具有不同特性, 并最终影响多普勒测流分辨能力[1]。上世纪80 年代, 多普勒测流以发射单频脉冲信号为主, 系统硬件实现过程较简单, 发射单频脉冲信号时难以同时具备较高测量精度和作用距离[2]。到上世纪90 年代初, 随着宽带测流技术的发展, 发射编码相干脉冲信号不仅具有较高的空间分辨力, 同时具有较高测量精度和较大作用距离[3]。近年来, 针对多普勒测流原理和应用领域,国内学者做了一定的探讨[1-2,4-6], 但对于多普勒测流时信号及其参数设计方面尚未做系统研究。
文中在多普勒测流实际应用背景下, 选取具有大时宽带宽乘积的Costas频率编码信号和几种相位编码信号, 从发射信号对测速精度和距离分辨力的影响, 以及对混响的抑制能力几方面进行了综合分析和比较, 以期为多普勒测流的波形设计提供参考。
1 波形设计要求
就测流精度和分辨能力而言, 较高的测距精度和距离分辨力要求发射信号具有较大带宽, 较高的测速精度和速度分辨力要求发射信号具有较大时宽。则发射信号[7]

表示成复指数形式, 即
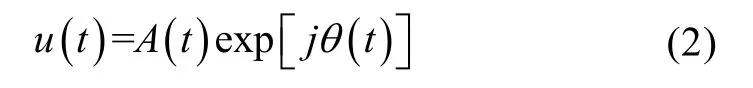

可见, 信号的均方根持续时间是由信号的振幅调制函数决定的, 信号的均方根带宽是由振幅调制和相位调制决定的。因此可以采用非线性相位调制, 脉冲内线性调频信号、相位编码信号和频率编码信号; 采用幅度调制, 通过脉冲调幅与增加信号持续期得到相干脉冲串信号。
海洋环境十分复杂, 声信号在实际传播中会受到损失, 因此选择的发射信号应具有良好抗混响性能, 在实际测流时要求测量结果的表征方差低。
1.1模糊函数
发射信号的分辨性能通过对其模糊函数进行分析得出。定义信号的模糊函数[4]

式中: τ为时延; ϕ为频移。
经过推导可知两回波信号的均方差2ε与模糊函数的关系
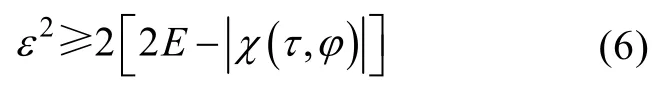
式中, E表示信号的能量。
在观察分辨力时, ε2越大, 表明2个目标参量差别越大, 越容易分辨。从式(6)可得, 当信号能量E确定时, χ(τ, ϕ)唯一地决定着系统对目标的分辨能力。χ(τ, ϕ)随τ和ϕ增大而下降得越迅速, 则ε2越大, 2个邻近目标就越容易分辨。
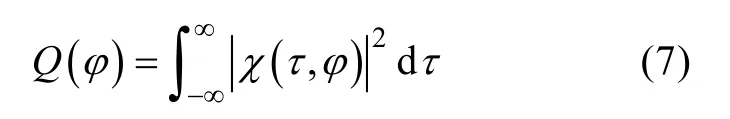
1.2多普勒测速算法
复自相关算法是目前比较常用的多普勒频率估计方法, 主要思想是确定两段回波信号之间的幅值和相位关系, 从而确定两段回波信号之间的频率。
发射信号表示为复指数形式
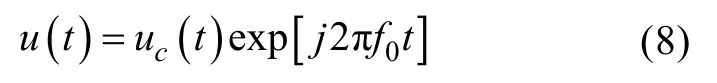
根据运动点目标回波模型其回波为

式中:τ0表示时延;fd表示多普勒频移。
经过低通滤波器(low pass filter, LPF)滤除其高频成分后的信号
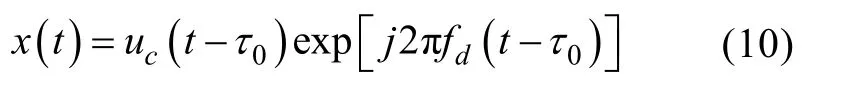
其自相关函数
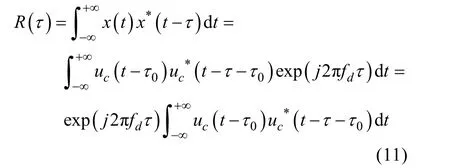
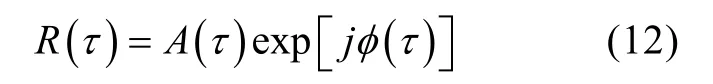
实际中, 散射回波信号是实信号, 在实际应用中可通过相互正交的两路信号分别与接收的回波信号做乘法运算, 得到混频信号, 然后通过LPF滤除高频部分, 最后进行复相关运算估计多普勒频移 fd,其原理见图1所示。
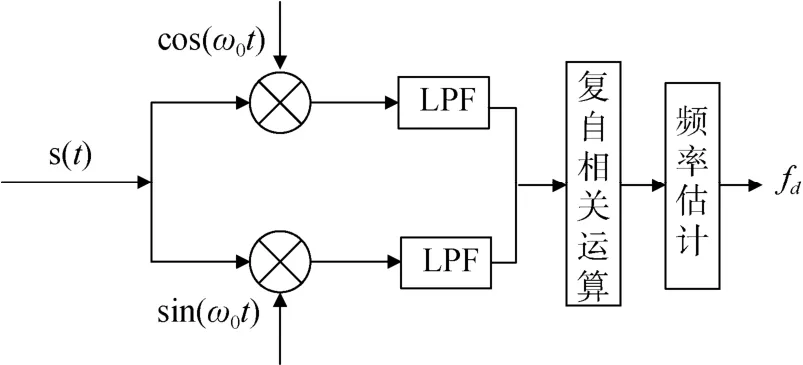
图1 信号处理框图Fig. 1 Block diagram of signal processing
1.3流层分析
多普勒测流要得到整个海流的1个剖面, 需要考虑层厚的大小和各层之间的分辨能力。因此,选择发射信号形式必须与剖面层厚分辨情况保持一致。
2 测流波形比较
2.1LFM-Costas频率编码信号
Costas脉冲编码信号是一种跳频信号, 其子脉冲中心频率由Costas编码控制。自相关函数副瓣最大值为1的序列, 称为Costas序列。Costas编码信号定义如下

式中:pn为子脉冲;Ts为子脉冲周期长度。子脉冲为LFM信号形式时定义为
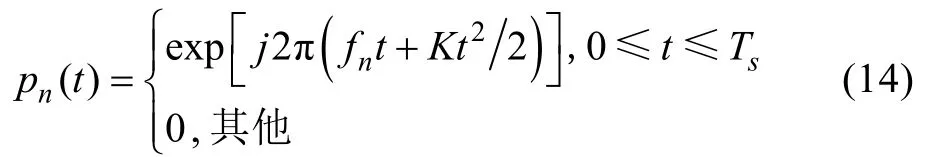
式中:fn为子脉冲的中心频率;K为调频斜率, 且K=/BT。假定信号中心频率为 f0, 带宽为B,则码元为θn的 Costas编码信号各子脉冲对应的频率为
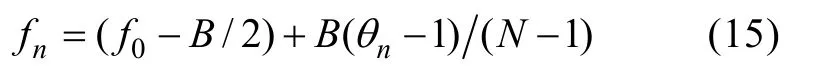
模糊函数
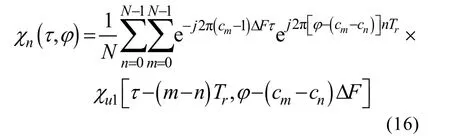
式中:Tn为脉冲重复周期;FΔ为子脉冲频率变化量。

图2为模糊函数示意图, 图中l表示距离, v表示速度。
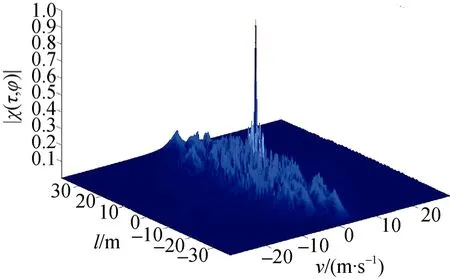
图2 LFM-Costas频率编码信号模糊函数Fig. 2 Ambiguity function of LFM-Costas frequency- coded signal
2.2M进制相移键控信号
M进制相移键控(multiple phase shift keying,MPSK)信号是一种相位编码信号[9], 其中较常用的有2PSK(BPSK), 4PSK (QPSK)和8PSK。其时域表示为

其中
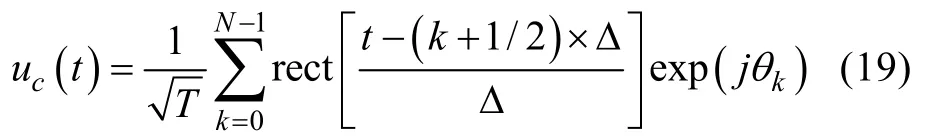
式中: Δ为码元宽度; N是码长;θk为码元的相位。在0~2π内取M个不同值(通常为等间隔),即

其模糊函数(参见图3)为
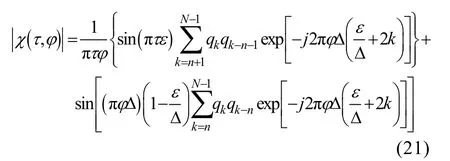
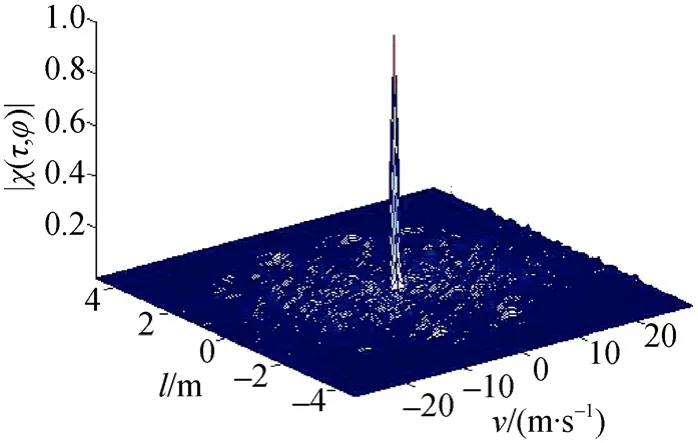
图3 M进制相移键控(MPSK)信号模糊函数Fig. 3 Ambiguity function of multiple phase shift keying(MPSK) signal
2.2.1二进制相移键控信号
二进制相移键控(binary phase shift keying,BPSK)信号载波的相位随调制信号 1或 0改变,通常用相位0°和180°分别表示1或0, 其时域为
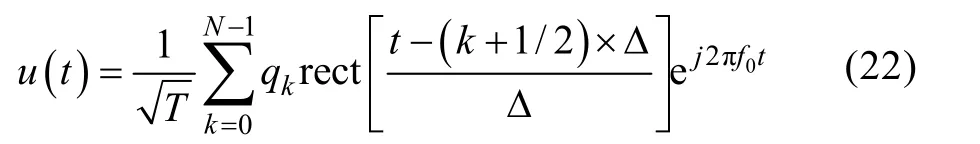
2.2.2其他MPSK信号
MPSK信号载波的相位通过Frank相位编码方式确定。其中 QPSK信号的相位取值范围为θk∈,8PSK信号载波相位的取值范围为:;16PSK信号的相位取值范围:,,。
从 Costas信号和 PSK信号的模糊度函数图可以看出, 2种信号都具有尖峰状模糊函数, 故他们都具有较好的时间-频率联合分辨力, 但Costas信号的模糊函数周围有较高的旁瓣, 而PSK信号的模糊函数旁瓣很低, 几乎可以看做“钉板状”,因此, 其抗干扰能力更强。
3 计算机仿真与分析
3.1信号模糊函数比较
仿真条件: 信号中心频率 f0=24kHz,采样率Fs=80kHz ,带宽B=6kHz,总脉冲长度为60ms。图4给出了CW信号、BPSK信号、4PSK信号、8PSK信号、16PSK信号和LFM-Costas频率编码信号的时间和频率分辨力的仿真比较结果,图5给出了各信号抗混响能力的仿真比较结果。

图4 不同MPSK信号距离和速度分辨力Fig. 4 Range and velocity resolution of different MPSK signals
从图 4可以看出, 频率编码信号和相位编码信号均能够同时具有较高的时间和频率分辨力,相比于其他信号, BPSK信号的时域自相关尖峰更加狭窄, 且旁瓣更低, 从而有利于获得高的测距精度和距离分辨力。从图5可以看出, BPSK相位编码信号在低速(5m/s以内)时具有较好的抗混响能力。纵坐标A表示归一化幅度。
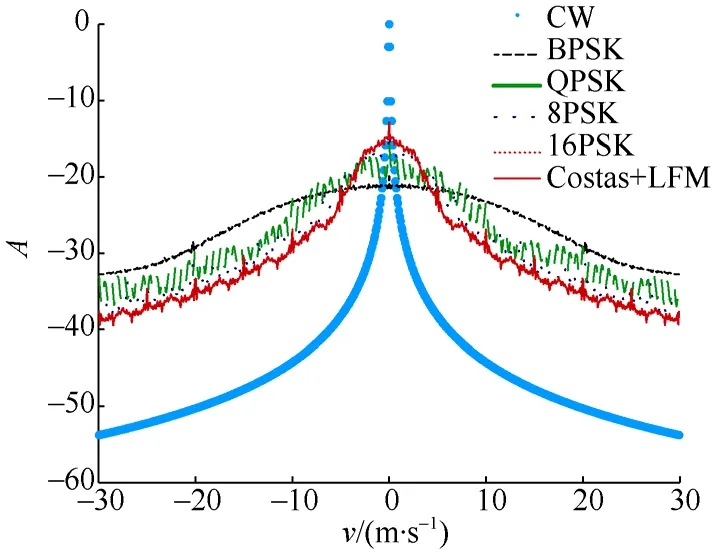
图5 不同信号抗混响能力Fig. 5 Comparison of anti-reverberation abilities among different signals
3.2信号多普勒测速精度比较
仿真条件: 带宽B=75kHz ,载波频率f0= 300kHz,信号持续时间 T约4.5ms(T=NΔNr,且Nr为重复次数,因各信号编码形式不同,码长和重复次数不同, 故持续时间在4.5ms左右),入射角30°,水中声速c=1500m/s , 根据文献错误!未找到引用源。,单次径向测速标准差σv可表示

式中: λ为信号的波长。可以看出信噪比(SNR)在某一阈值以下时, 测速精度随SNR增大而减小,在SNR较大时, 增大SNR对多普勒测速精度的影响相差不大, 文中选SNR=20dB, 估计理论速度在[0.05,0.5]区间内每隔 0.05m/s选取。采用复协方差估计多普勒频移, 在不同理论速度下得到速度估计的标准方差σv, 如图6所示。估计理论速度v=1m/s , 在不同SNR下得到速度估计的标准方差σv, 如图7所示。
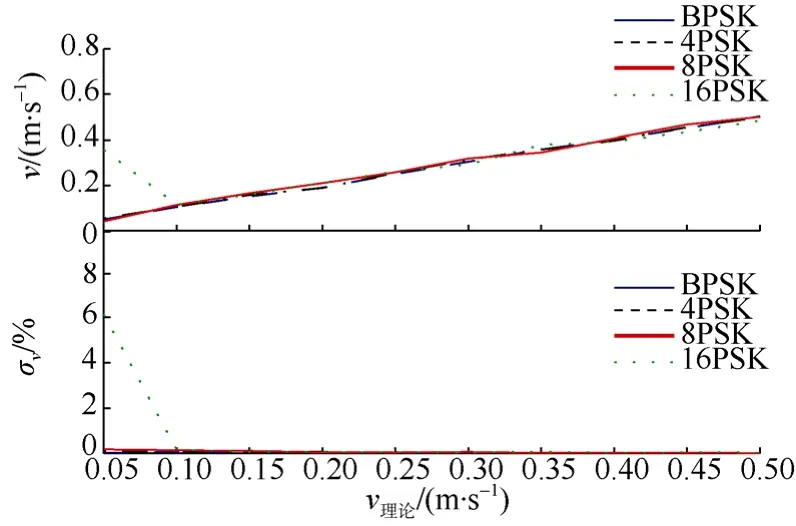
图6 SNR=20 dB时的测速均值Fig. 6 Average velocity when SNR=20 dB

图7 v =1 m/s时测速均值Fig. 7 Average velocity when v=1 m/s
其中
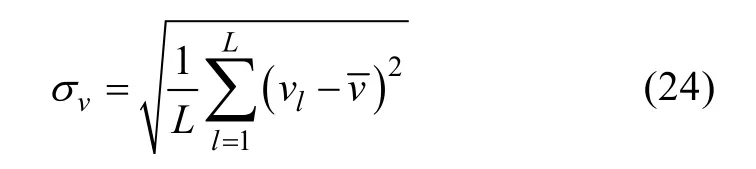
4 结束语
文中基于多普勒测流实际应用背景, 选取Costas频率编码信号和几种相位编码信号, 通过比较信号的模糊函数, 得出BPSK信号更加有利于获得高的测速精度和距离分辨力, 且在低速条件下具有较好的抗混响能力。仿真不同发射信号条件下, 采用复自相关算法估计多普勒频率的精度比较发现, 在相同的信噪比和理论速度下, 发射BPSK信号测量得到的速度表征方差最小, 与理论分析一致。后续, 将针对波形各参数对测速精度的影响展开研究。
[1] 刘德铸. 声学多普勒流速测量关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
[2] 张殿伦. 舰船声学测速技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2001.
[3] Brumley B H, Cabrera R G, Deines K L, et al. Performance of a Broad-band Acoustic Doppler Current Profiler[J], IEEE Journal of Oceanic Engineering, 1991, 16(4): 402-407.
[4] 刘征宇, 陈允锋, 陈梦英. 基于 Modbus协议的声学多普勒流速剖面仪软件实现[J]. 声学技术, 2015, 34(3): 260-264. Liu Zheng-yu, Chen Yun-feng, Chen Meng-ying. Implementation of Acoustic Doppler Profilers Based on Modbus Protocol[J]. Technical Acoustics, 2015, 34(3): 260-264.
[5] 黄毅. 声学多普勒测流仪原理及应用[J]. 气象水文海洋仪器, 2013(4): 119-122. Huang Yi. Principle and Application of Acoustic Doppler Current Profilers[J]. Meteorological, Hydrological and Marine Instruments, 2013(4): 119-122.
[6] 张春海, 董晓冰. 声学多普勒测流原理及应用研究[J].吉林水利, 2013(11): 17-19.
[7] 李志舜. 鱼雷自导信号与信息处理[M]. 西安: 西北工业大学出版社, 2004.
[8] 陈韶华, 赵冬艳. 几种主动声呐信号抗混响性能分析[J]. 水雷战与舰船防护, 2011, 19(4): 12-15. Chen Shao-hua, Zhao Dong-yan. Reverberation Suppression Performance of Several Active Sonar Signals[J]. Mine Warfare & Ship Self-defense, 2011, 19(4): 12-15.
[9] 朱埜. 主动声呐检测信息原理[M]. 北京: 科学出版社,2014.
[10] Theriault K. Incoherent Multibeam Doppler Current Profiler Performance: Part II—Spatial Response[J]. IEEE Journal of Oceanic Engineering, 1986, 11(1): 16-25.
(责任编辑: 杨力军)
Waveform Analysis of Acoustic Doppler Flow Measurement
ZHANG Yu-hang1,2,YANG Yun-chuan1,LÜ Lin-xia1,WANG Hai-lu1,YUE Ling1,LI Jin-ming1
(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710077, China)
To improve the velocity accuracy and range resolution of Doppler flow measurement technology, this paper comprehensively compares the waveforms of the signals with large product of time-width and bandwidth between the Costas frequency-coded signal and several phrase-coded signals considering practical application condition. It is revealed that binary phase shift keying(BPSK) signal is more benefitial to achieving high velocity accuracy and range resolution, and gains better anti-reverberation ability at low speed. The accuracy of Doppler frequency is estimated in simulation by using the complex autocorrelation algorithm. The results show that BPSK signal can help to obtain the minimum variance of velocity characterization, and is more suitable for the measurement of high-resolution Doppler flow velocity.
Doppler flow measurement; waveform analysis; binary phase shift keying(BPSK); Costas frequency coding
TJ630.34; TB56
A
1673-1948(2016)05-0329-05
10.11993/j.issn.1673-1948.2016.05.003
2016-05-31;
2016-07-13.
张宇航(1993-), 女, 在读硕士, 研究方向为声自导信号处理技术.

