基于测点优化和加速度计的叶轮模态测试

刘景云，　孙　涛，　彭　博，　伊　寅，　严　海，　高慧中

（1. 中国船舶重工集团公司 第705研究所， 陕西 西安， 710077； 2. 水下信息与控制重点实验室， 陕西 西安，710077）

基于测点优化和加速度计的叶轮模态测试

刘景云1，2，孙涛1，彭博1，伊寅1，严海1，高慧中1

（1. 中国船舶重工集团公司 第705研究所， 陕西 西安， 710077； 2. 水下信息与控制重点实验室， 陕西 西安，710077）

鱼雷涡轮机叶轮体积小、质量轻， 加速度传感器的数量对叶轮模态的测试精度和可测阶数有直接影响。为了尽可能减少测点数目以降低附加质量对叶轮固有频率的影响， 将叶轮有限元网格模型及模态计算结果导入LMS Virtual.lab中进行模态置信度分析， 优化出叶轮模态试验的响应测点数量和位置， 以及激励点的位置和方向。以预试验分析结果为指导， 采用加速度传感器测量出叶轮前3阶固有频率和振型。试验模态和计算模态的振型基本一致， 固有频率最大相对误差为3.3%。研究表明， 对传感器的位置和数量进行优化后可提高涡轮机叶轮模态测试效果， 但无法完全消除附加质量对叶轮固有频率的影响， 建议采用非接触激光测振技术来获取精确详细的叶轮模态参数。

鱼雷涡轮机； 叶轮； 有限元； 预试验； 模态测试

0　引言

鱼雷涡轮机的涡轮盘质量平衡、涡轮叶片不均匀气流脉动及高速气流通过涡轮叶片产生的气动噪声皆为涡轮机振动和噪声的主要来源。为了避免涡轮机叶轮在发动机升速、部分进气脉冲激励力影响下发生共振， 增大振动噪声甚至危及发动机的安全运行， 非常有必要准确获取叶轮的模态。赵军等利用有限元分析软件ANSYS 的循环对称方法对某燃气涡轮机叶轮进行了模态分析，并对前12阶振型进行了讨论［1］。李日朝等分别采用传递矩阵法和有限元法对某高速转子的临界转速（固有频率）进行求解， 通过试验测试了最大振幅对应的转速［2］。

然而由于鱼雷涡轮机具有结构紧凑、比功率大、转速高等设计要求， 其叶轮也具有体积小、质量轻的特点［3］。由叶轮的结构特点不难看出，传统基于加速度传感器的模态测试方法必然会增加与叶轮无关的附加质量， 从而影响模态测试精度和可测阶数。从目前公开资料来看， 鲜有关于鱼雷涡轮机叶轮模态的试验研究， 传感器可测出的模态阶数及固有频率精度尚不可知， 仍有研究的必要性。此外， 随着仿真技术的发展， 试验前对模态测点和激励点进行优化的方法和软件日渐成熟［4-5］， 这在一定程度上可降低附加质量的影响。

文中基于测点优化和加速度计的涡轮机叶轮模态测试方法， 首先建立叶轮有限元模型， 计算出叶轮前 10阶模态的固有频率和振型； 其次结合叶轮的结构特点， 研究适用于叶轮模态测试的测点和激励点布置方案， 并以此来指导叶轮模态试验； 最后分析叶轮模态测试结果并与有限元计算结果进行比较， 指出了传感器测量叶轮模态的局限性及更为适用的测试手段。

1　叶轮有限元模型及计算模态

将建好的3D几何模型导入ANSYS中进行材料定义、网格划分和施加边界条件。叶轮盘与叶片是一体加工而成， 材料弹性模量为 221 GPa，泊松比为0.33， 密度8 390 kg/m3， 选择自由边界条件。采用 Solid92单元对实体模型进行网格划分， 结果如图1所示。

图1　叶轮有限元网格模型Fig. 1　Finite element grid model of an impeller

表1为叶轮有限元模型的前10阶模态固有频率分布。从分析结果得知， 除叶轮轴向呼吸模态外， 同一节径下对应的相近固有频率具有2种振动方式一样、振动相位相差一定角度的振型，这是因为完全对称结构的2个相似振型对应的固有频率重合。

表1　叶轮模态及振型Table 1　Impeller modal and vibration mode

建立叶轮有限元模型时， 对其外缘倒角进行了简化， 因此有限元模型与实际结构之间有一定的偏差， 必然会对模态分析的结果产生影响。但对于结构较复杂的叶轮， 利用有限元计算结果能够获知感兴趣的固有频率分布情况， 确定测试设备的采样频率， 为响应点和激励点的优化提供输入， 为模态试验结果的评判提供参考。

2　叶轮模态响应点和激励点优化

叶轮模态响应点和激励点优化， 即预试验分析的目的是在无冗余、无泄漏地获得各阶模态的基础上， 尽可能减少测点数目降低附加质量的影响； 选取的激励点能够充分激起尽可能多阶的模态， 从而提高模态测试的质量和效率。

2.1响应测点优选准则

在进行预试验分析时， 如果所给测点数目较少不能保证足够的自由度数而使模态的相关性较低， 就会导致2阶不同模态相似而无法识别。为此， 引入模态置信判据（modal assurance criterion，MAC）来表示模态的可信程度， 并以此来评价或验证模态， 进而评估所选测点的数目和质量好坏［6-7］。

式中: 矩阵Vk表示一组多个模态振型；Vjk，Vlk分别表示留数矩阵Rk的第j， i列； T表示复共轭转置。

如果复向量Vjk和Vlk之间存在线性相关，则MAC的值接近于 1（100%），如果二者线性独立，则MAC值会接近于0。因此借助MAC矩阵即可表明每对振型间的相关程度。当处于非对角线上的 MAC值较大时， 说明不同阶的模态振型之间相关性较高， 振型互相混淆难以识别， 需增加测点数量来增加振型的自由度数。

2.2激励点优选准则

为了能够充分激起尽可能多阶的模态频率，采取驱动点留数（driving point residues， DPR）方法来优化激励点的位置和方向［6-7］。用表示被测试件在f点激励、e点获取的响应函数

式中: ω表示模态固有频率；λr表示第 r阶模态的特征值；Aefr表示驱动点f在e自由度处第r阶模态的留数。

在纯模态情况下， 如果按单位模态质量换算，模态比例系数可表示为

式中:erψ 表示在驱动点e自由度处第r阶模态的振型系数；rω表示第r阶模态频率。DPR值较大的激励位置可激起较多模态， 故选择DPR值最大处为最佳激励点。

2.3叶轮响应测点和激励点优选

由于叶片尺寸很小， 无法在其表面布置传感器， 为减少划分网格的冗余工作， 除去叶片及外围裙带部分结构， 以此来等效叶轮进行预试验分析。将叶盘的网格划分模型和模态计算结果导入LMS Virtual.lab软件中的振动与噪声相关性分析模块。在叶轮有限元模型外表面选取一组数量最少、能基本反映叶轮结构外形的一组测点作为初始测点组， 共10个测点， 具体布置如图2所示。

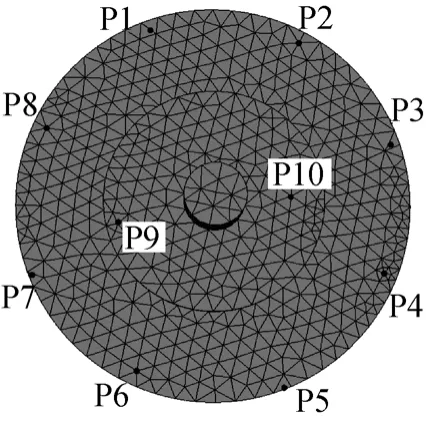
图2　初始测点Fig. 2　Initial measuring points

对叶轮盘进行预试验分析， 根据选定基本测点组对各阶模态振型作相关性分析， 得到模态置信准则图， 如图3所示。由图 3可知， 处于非对角区域的 MAC 值较高， 其中高于 0.5的模态对的 MAC 值见表 2， 表明该模型在这几对模态振型间存在相关情形， 如果测点不足， 难以捕捉局部变形， 模型的振型容易发生空间混淆现象。

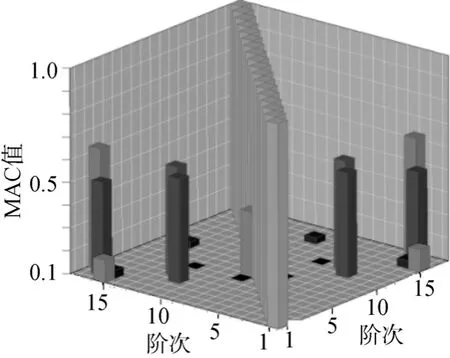
图3　初始测点模态置信判据（MAC）图Fig. 3　Modal assurance criterion（MAC） diagram of initial measuring points

表2　初始模型非对角线MAC值Table 2　Off-diagonal MAC value of initial model

为清晰辨识相关模态对， 在叶盘内圈上增加2个测点（见图4）， 经分析得增加测点后MAC值如图5所示， 非对角区域的MAC值除18～19模态对（约 0.4）外均低于 0.2， 可明显辨识低阶模态振型， 测点布置比较准确， 由此确立叶盘模态试验的测点布置方案。

对上述方案所有测点各自由度下的 DPR进行计算和分析， 按 DPR值由大到小列举前 7个不同激励位置的 DPR加权平均值， 如图 6所示。由图可知， 叶盘的测点1的+X方向DPR 加权平均值最大， 在这点激励可以较好的激起结构的各阶模态， 由此确立叶盘模态试验的激励点位于点P1的背面， 记为P13。

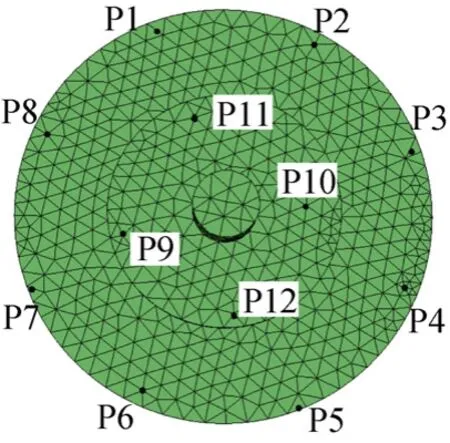
图4　增加测点后的叶轮测点分布Fig. 4　Measuring point distribution on impeller after increasing measuring points

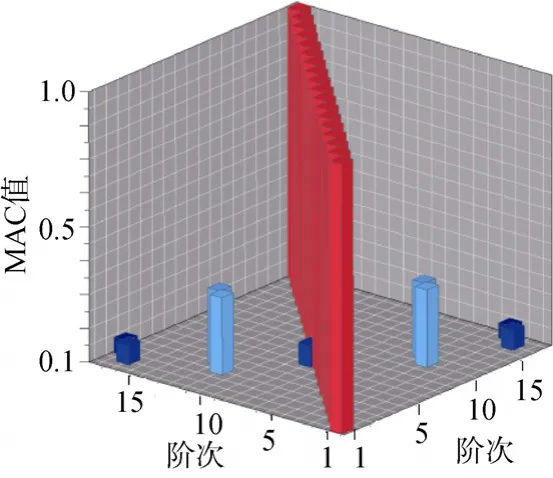
图5　增加测点后MAC图Fig. 5　MAC diagram after increasing measuring points

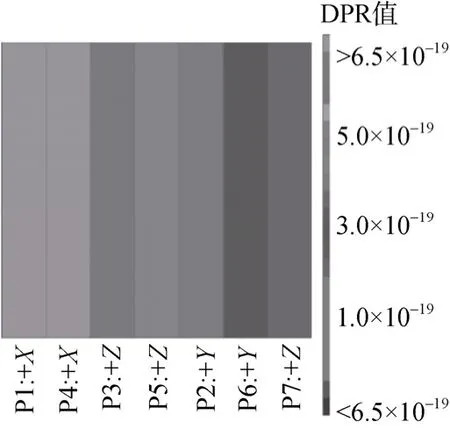
图6　测点驱动点留数（DPR）加权平均值Fig. 6　Driving point residues（DPR） weighted average value of measuring points

3　叶轮模态测试

3.1模态试验方案和测试系统

使用橡皮绳弹性悬挂叶轮模拟自由边界条件，用东华公司的LC02电压型力锤施加脉冲激励。采用PCB传感器测量振动加速度， 模态分析软件为LMS Test.lab12A。考虑到叶轮尺寸较小， 难以同时布置12个传感器， 同时为了降低传感器的附加质量， 故分3次进行测量， 每次只测4个点。

测试系统如图 7， 给激励信号加力指数窗来提高信噪比， 响应信号加指数窗来提高频响函数精度。为获得较宽频带的激励信号， 力锤选用硬度大的钢质锤头， 通过观察激励点的功率谱分布趋势， 结果显示在4 096 Hz频率范围内能较好地激起前3阶固有频率， 从而确定带宽选取范围。

图7　叶轮模态测试系统Fig. 7　Measurement system of impeller modal

3.2模态试验结果分析

剔除相干函数较差、锤击效果不佳的测试数据， 记录 5次测量平均值， 获得各个测点的加速度频率响应信号。在 LMS结构振动分析软件中选取所有测点的功率谱之和， 将传感器采集的响应信号除以力锤的输入力参考信号得到频响函数曲线（见图8）。

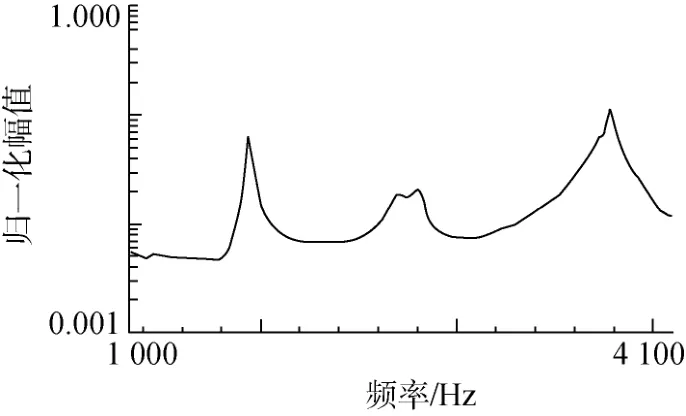
图8　所有测点的频响函数总和Fig. 8　Sum of frequency response function of all measuring points

采用 PloyMAX算法进行模态分析， 选取谱线中S点（Stable）最多的峰值作为极点， 并识别出各阶模态振型， 结果显示与有限元分析前 3阶振型一致（见图9）。附加质量前后测点的响应信号对比见图10。由图可见， 在每阶振型处都存在相邻谱峰重叠现象， 2阶和3阶尤为明显， 通过观察发现 2个相邻峰值对应的振型一致， 振型的节径互成一定角度。参考有限元分析结果， 其同阶互成角度的相似振型对应固有频率相差不超过 5 Hz，而加速度测量结果显示相似振型对应的固有频率相差高达几十赫兹， 误差较大。

为了验证加速度传感器附加质量对叶轮固有频率的测试结果影响程度， 在叶轮盘的正反两面各选取一个测点， 保证两测点处于径向和周向同一位置。先在正面布置单个传感器测量叶轮的固有频率， 再在反面布置一个传感器作为附加质量进行测量， 2次测得的功率响应谱线如图10所示。

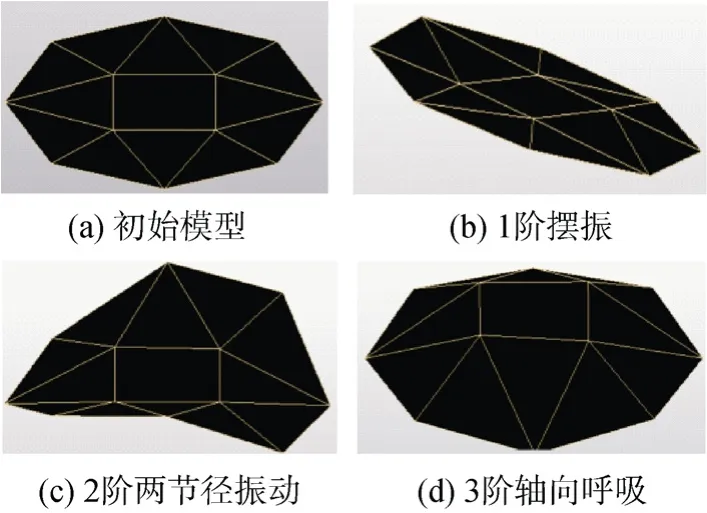
图9　叶轮盘测试振型Fig. 9　Measured vibration mode of impeller plate

图10　附加质量前后测点的响应信号比较Fig. 10　Response signal comparison of measuring points between before and after additional mass

测试结果显示用单个传感器测量时正面测点的第 2阶固有频率处谱峰出现轻微重叠现象（实线）， 2个峰值相距较近； 反面附加1个传感器后进行测量时正面测点第2阶固有频率处有明显双谱峰（虚线）， 且2个峰值相距较远。由此可知传感器的附加质量对叶轮的固有频率有一定影响。故认为单个传感器所测的固有频率更准确， 同样采用PloyMAX算法获得叶轮前3阶固有频率见表 3。测试结果与对应振型的有限元计算结果对比， 其误差不超过4%。

表3　叶轮固有频率Table 3　Natural frequencies of an impeller

4　结 论

文中在对叶轮模态测点位置和数量进行优化的基础上， 采用加速度传感器测量了叶轮模态。结果表明， 采用压电式加速度传感器只能获取叶轮前3阶固有频率， 相对计算模态的最大误差为3.3%；加速度传感器的附加质量对叶轮固有频率的测量精度影响较大， 会引起双峰现象。显然， 对测点进行优化后可提高涡轮机叶轮模态测试效果， 但无法完全消除附加质量影响， 建议采用无附加质量的非接触式激光测振技术测量叶轮模态。

［1］ 赵军， 单晓亮， 樊晓波. 水下航行器燃气涡轮机叶轮模态分析［J］. 鱼雷技术， 2011， 19（3）: 214-217. Zhao Jun， Shan Xiao-liang， Fan Xiao-bo. Modal Analysis of Gas Turbine Impeller for Underwater Vehicle［J］. Torpedo Technology， 2011， 19（3）: 214-217.

［2］ 李日朝， 郝东旭. 燃气涡轮机高速转子临界转速仿真［J］. 鱼雷技术， 2014， 22（6）: 457-460. Li Ri-zhao， Hao Dong-xu. Simulation on Critical Rotation Speed of High-Speed Rotor of Gas Turbine［J］. Torpedo Technology， 2014， 22（6）: 457-460.

［3］ 查志武， 史小锋， 钱志博. 鱼雷热动力技术［M］. 北京:国防工业出版社， 2006.

［4］ 严海， 马锐磊， 梁跃， 等. 基于模态参数水下航行器楔环结构有限元模型修正［J］. 鱼雷技术， 2016， 24（2）: 87-93. Yan Hai， Ma Rui-lei， Liang Yue， et al. Finite Element Model Correction for Wedged-Ring Connection Structure of Underwater Vehicle Based on Modal Parameters［J］. Torpedo Technology， 2016， 24（2）: 87-93.

［5］ 张喜清， 项昌乐， 刘 辉， 等. 基于预试验分析的复杂箱体结构试验模态研究［J］. 振动与冲击， 2011， 30（4）: 109-112. Zhang Xi-qing， Xiang Chang-le， Liu Hui， et al. Modal Testing Study on a Complicated Housing Structure Based on Pre-test Analysis［J］. Journal of Vibration and Shock，2011， 30（4）: 109-112.

［6］ Lallement G. Optimal Selection of the Measured Degree of Freedom and Application to a Method of Parameter Correction［C］//Proceedings of the 9th International Modal Analysis Conference（IMAC）. New York: Union College，1991: 972-976．

［7］ LightTrans. LMS Virtual.lab: Noise＆Vibration Pre-test Theoretical Background［M］. Jena， Germany: LightTrans，2004.

（责任编辑: 许妍）

Impeller Modal Testing Based on Measuring Points Optimization and Acceleration Sensors

LIU Jing-yun1，2，SUN Tao1，PENG Bo1，YI Yin1，YAN Hai1，GAO Hui-zhong1
（1. The 705 Research Institute， China Shipbuilding Industry Corporation， Xi′an 710077， China； 2. Science and Technology on Underwater Information and Control Laboratory， Xi′an 710077， China）

Since torpedo turbine impeller is small and light， the number of acceleration sensors has a direct effect on testing precision and measured order of impeller modal. In order to reduce the number of testing points for the purpose of decreasing the effect of additional mass on the natural frequency of the impeller， modal confidence analysis is carried out by introducing the finite element grid model and the modal calculation result of the impeller into the software LMS Virtual.lab. The response number and positions of the measuring points， as well as the position and direction of the excitation point， in impeller modal testing are optimized. The first 3 orders of natural frequency and vibration modes of the impeller are identified with acceleration sensors on the basis of pre-test. The vibration modes of the modals from testing coincide with that from calculation， and the maximum error of natural frequency is 3.3%. This research indicates that the optimized position and number of sensors can improve modal testing effect， but cannot eliminate the influence of additional mass on the natural frequency of the impeller completely. It is suggested that the non-contact laser vibrameter technology be employed to obtain more accurate impeller modal parameters.

torpedo turbine； impeller； finite element； pre-test； modal testing

TJ630.32； TP35

A

1673-1948（2016）05-0357-05

10.11993/j.issn.1673-1948.2016.05.008

2016-06-12；

2016-07-07.

船舶工业国防科技预研基金项目（14J4.4.1）.

刘景云（1991-）， 男， 在读硕士， 主要研究方向为测试测量技术.