等效约束下风激励汽车前侧窗玻璃声辐射分析

贺银芝， 石子豪， 吕 越， 杨志刚

(1.同济大学 汽车学院， 上海 201804；2.上海市地面交通工具空气动力与热环境模拟重点实验室， 上海 201804)

汽车高速行驶时，除泄漏噪声外，驾驶员耳旁位置处的气动噪声主要包括由侧窗玻璃表面压力脉动激起玻璃振动向车内辐射的噪声以及周围湍流发声而传透到车内的噪声组成.因此，研究侧窗在风载荷激励下向车内辐射或传透噪声的机理，对于减小车内噪声，提升汽车驾乘舒适性具有重要意义.本文研究内容主要关注由侧窗玻璃表面压力脉动激起玻璃振动而向车内辐射噪声的问题.

汽车侧窗玻璃由密封条约束，它具有支撑车窗玻璃、提高车身密封性、防水防尘、隔声降噪等功能，结构形状与特性复杂.由于密封条大多使用超弹性橡胶材料，其约束具有几何非线性、材料非线性及边界条件非线性，因此车窗玻璃边界约束模型的建立较为困难.为了研究侧窗玻璃约束条件，便于后续工作的开展，需要将密封条进行等效简化处理.此外，本文利用Corcos模型半经验公式计算湍流脉动压力的分布，作为侧窗玻璃系统的激励，计算其声辐射.

国内外已有一些学者对侧窗系统的简化以及Corcos模型进行了相关研究.对于侧窗系统的简化，Tuncer等[1]运用等效替代的方法，使用弹簧单元代替橡胶密封条，研究了车身结构的振动对车内噪声分布的影响；Dikmen等[2]通过建立车门密封条的超弹性材料模型来预测车门的动态特性；朱文峰等[3]将导槽-玻璃等效为弹性密封约束，并基于车窗密封条唇边压缩试验数据确定弹簧刚度，探究了弹簧支撑的车窗系统建模的有效性.对于Corcos模型，Coney等[4]通过试验的方法，采集侧窗表面的压力脉动分布数据，确定Corcos模型的各项参数，从而通过理论公式计算侧窗的振动响应.Han等[5]使用Corcos模型探究了在压力脉动激励下薄板结构的振动特性和声辐射，指出Corcos模型更适合于非均匀的分离流及再附着流的计算.

本文以某轿车左前侧窗为研究对象，首先通过等效替代，将车窗密封条等效成弹簧约束，对其进行离散化建模并验证其有效性.接着使用Corcos模型模拟侧窗表面压力脉动，得到压力功率谱密度，作为侧窗等效模型的激励，计算车内噪声.最后利用激光测振仪所测侧窗表面速度分布数据，基于边界元(BEM)方法(半仿真)，计算玻璃振动辐射到车内的噪声，并与基于Corcos模型的有限元(FEM)计算结果进行对比，检验利用等效简化模型与Corcos模型计算风激励下汽车侧窗玻璃声辐射的适用性.

1 建立前侧窗玻璃系统等效模型

根据功能等效原理以及密封条压缩作用力-位移关系可以近似用一次函数表示的假设，将密封条等效成弹簧约束.利用基于遗传算法的Matlab-Abaqus联合仿真，以模态试验测得的侧窗各阶固有频率为目标值，拟合出等效弹簧的刚度.比较等效模型与真实侧窗的各阶模态振型以及频响函数，验证等效模型的有效性及可靠性.

1.1 试验模态分析

为获取试验车前侧窗玻璃系统的动力学特性，并且给下文离散模型刚度拟合提供目标值，对真实边界约束下的侧窗玻璃应用锤击法进行模态试验.试验采用多点激励、单点响应的方法.在前侧窗玻璃的表面布置34个激振点，通过顺次移动力锤，敲击激励点采集激励力信号，同时在车窗的右上角31点位置处布置一个拾振点，固定单向加速度传感器，用于同步采集力锤敲击下的车窗玻璃加速度响应信号.试验设备及测点位置如图1所示.

图1 侧窗玻璃系统模态试验及玻璃表面测点分布Fig.1 Modal test of side window glass system anddistribution of test points on glass surface

试验采用德国HEAD acoustics公司数据采集系统，采样时间为5 s，采样频率为24 kHz.将试验中采集的侧窗玻璃所有频响函数进行拟合，获得该系统的各阶模态参数.表1所示为前4阶固有频率及阻尼比，图2所示为前4阶模态振型.

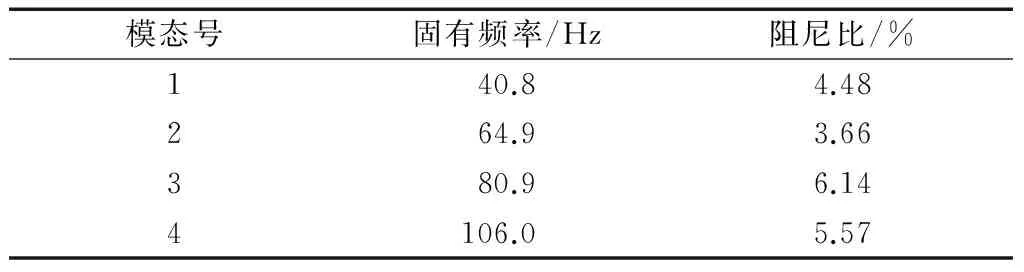
表1 侧窗玻璃系统前4阶试验固有频率与阻尼比Tab.1 First four orders of natural frequencies anddamping ratio of side window glass system

图2 侧窗玻璃系统前4阶试验模态振型

Fig.2Firstfourordersofmodalshapesofsidewindowglasssystem

从试验结果所得模态振型可以看出，在1阶固有频率下，侧窗玻璃绕着下方两个支撑销钉(图中未画出)进行前后摆动，类似于结构的刚体位移，但也存在局部的变形.在2阶固有频率下，侧窗玻璃绕着近似中线位置进行扭转变形.而3阶与4阶固有频率对应的振型为弯扭组合变形.

1.2 车窗边界约束条件等效原理

密封条的几何、材料及边界条件的非线性[6-7]问题使得车窗系统边界约束模型的建立非常困难.因此，本文基于等效原理，将侧窗玻璃顶部、侧面导槽密封条及底部水切密封条离散成弹簧的接触约束.弹簧刚度将通过基于遗传算法的Matlab-Abaqus仿真平台拟合获取.

1.3 有限元模型建立

为拟合弹簧的刚度，需要建立前侧窗玻璃有限元模型.本文通过对某车型前侧窗玻璃进行3D扫描，处理得到的侧窗玻璃三维模型如图3所示.对该模型进行三角形壳单元网格划分，最小网格大小为5 mm.侧窗玻璃材料属性见表2.

图3 侧窗玻璃三维模型Fig.3 Three-dimensional model of side window glass表2 侧窗玻璃材料属性Tab.2 Material properties of side window glass

材料名称密度/(kg·m-3)弹性模量/GPa泊松比钢化玻璃2260720.20

在车窗四周密封条各网格节点处建立弹簧单元，弹簧一端连接网格节点，另一端固定，方向为节点处玻璃表面的法线方向.由于模态试验玻璃四周测点位置与弹簧单元位置接近，所以测点处位移可近似表示为该测点附近弹簧单元的压缩量.由于模态试验第1阶振型近似于玻璃刚体位移，可通过第1阶振型得到四周测点位移，即弹簧单元压缩量.再利用弹簧刚度与压缩量成反比的关系，设测点2附近弹簧单元刚度为参考刚度K1，得到其余各刚度如表3所示.

由于实车车窗玻璃与车门之间采用销连接，所以玻璃底部销孔处约束也等效为弹簧约束，其弹簧刚度设为K2，如图4所示.

1.4 等效弹簧刚度拟合

为了快速模拟出最符合侧窗玻璃边界约束条件的弹簧刚度，减少人工处理数据的繁琐和出错概率，提高研究分析工作的效率，采用基于遗传算法的Matlab-Abaqus联合仿真平台寻找弹簧刚度的全局最优解.

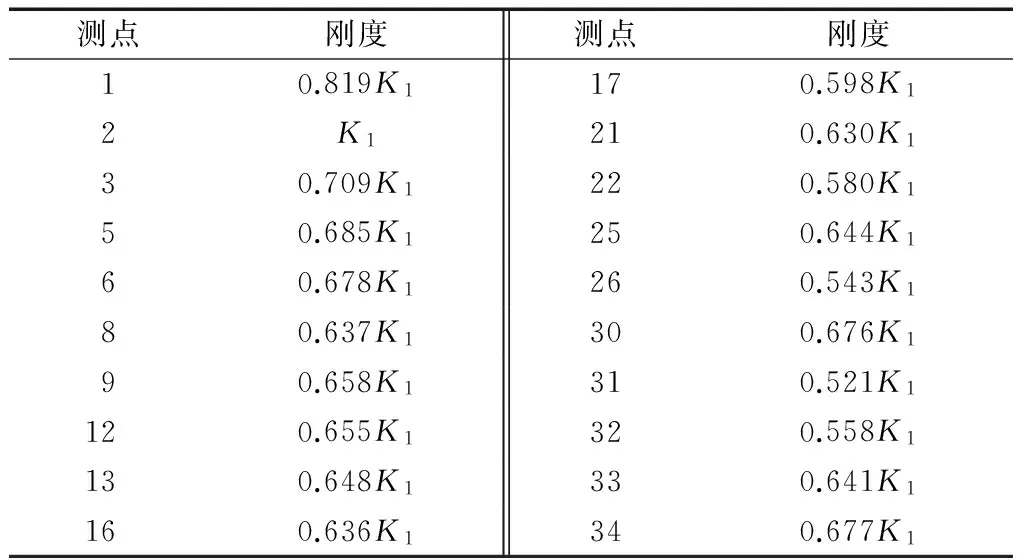
表3 测点附近弹簧刚度Tab.3 Stiffness of springs near measured points

图4 销钉孔弹簧刚度Fig.4 Stiffness of springs near pin holes

1.4.1设计目标

由于固有频率是系统的固有特性，为模拟真实车窗玻璃系统边界约束，得到最优弹簧刚度，采用固有频率标准差作为控制目标，其定义如式(1)所示.取前文模态试验所得到的前4阶固有频率与仿真值作标准差计算，其标准差越小，代表优化结果越好.

(1)

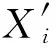
1.4.2Matlab-Abaqus联合仿真平台搭建

实现Matlab-Abaqus联合仿真平台进行侧窗玻璃弹簧刚度拟合的主要思路是利用Matlab修改Abaqus有限元模型的INP文件，并调用Abaqus /cae进行计算，Abaqus计算结束后，将计算结果返回Matlab进行结果分析，在遗传算法工具箱的驱动下进行迭代计算，最终使弹簧刚度拟合至最佳值[8-9].其联合仿真实现思路如图5所示.

在拟合过程中，由于Matlab无法识别Abaqus计算生成的ODB结果文件，所以不能直接提取Abaqus计算结果进行标准差计算.本文通过Abaqus提供的Python脚本接口，利用Python语言的可扩充性、可移植性、可嵌入性实现对Abaqus/cae的二次开发[10].最终Matlab通过Python脚本读取Abaqus计算结果，完成数据的提取.

图5 Matlab-Abaqus联合仿真流程Fig.5 Flow chart of Matlab-Abaqus co-simulation

1.4.3仿真结果分析

通过上述方法拟合得到的弹簧刚度K1=0.734 N·mm-1，K2=41.250 N·mm-1，控制目标(固有频率标准差)收敛于4.0，计算结果如图6所示.计算最终拟合模型前4阶固有频率如表4所示.

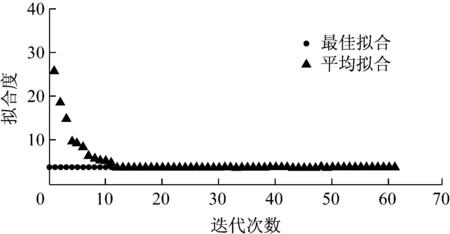
图6 固有频率标准差拟合结果Fig.6 Fitting results of standard deviation ofnatural frequencies表4 固有频率仿真值与试验值对比Tab.4 Comparison of simulated and experimentalnatural frequencies

模态号仿真固有频率/Hz试验固有频率/Hz147.240.8264.464.9379.280.94101.3106.0

1.5 结果验证

为了验证本文侧窗玻璃边界等效约束方法的可靠性，将试验结果与有限元仿真分析结果进行对比验证.

1.5.1模态振型验证

图7所示为侧窗玻璃前4阶固有频率对应的振型.对比发现二者的1阶固有频率对应的振型均类似刚体位移，但有局部弯曲变形，2阶固有频率对应的振型均为扭转变形，3、4阶固有频率对应的振型为弯扭组合变形.说明等效密封约束下的车窗与实际密封条约束下的车窗在各阶振型上具有良好的一致性.

图7 侧窗玻璃前4阶振型试验与仿真结果对比

Fig.7Firstfourordersofexperimentalandsimulatedmodalshapesofsidewindowglasssystem

1.5.2频响函数验证

图8a、8b分别为测点8、13相对于响应点31的频响函数试验与仿真对比图.从图8中可以看出，测点仿真与试验频响函数在低频区的峰值频率吻合较好，较高频段因为模态密集效应，峰值吻合有一定差别，但总体趋势较一致.

通过上述对比，发现仿真与试验结果吻合较好，从而证明了运用等效原理，以等效弹簧代替实际密封条约束，并基于遗传算法的Matlab-Abaqus联合仿真平台进行等效弹簧刚度拟合的方法是合理且有效的.

2 计算侧窗表面压力功率谱与车内声辐射

侧窗表面湍流中的涡结构彼此之间相互作用，使得涡不断地产生、脱落.在涡脱落的瞬间，会产生较大的压力脉动，而湍流边界层的压力脉动是引起车窗振动并向车内辐射噪声的主要原因.压力脉动是一个随机过程，没有必然的确定性变化规律，亦即不能用确定的函数加以描述，但是具有一定的统计规律，可以采用统计学的方法，利用相关函数与功率

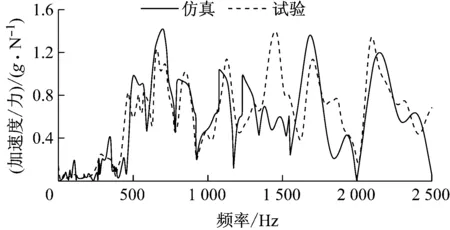
a 测点8

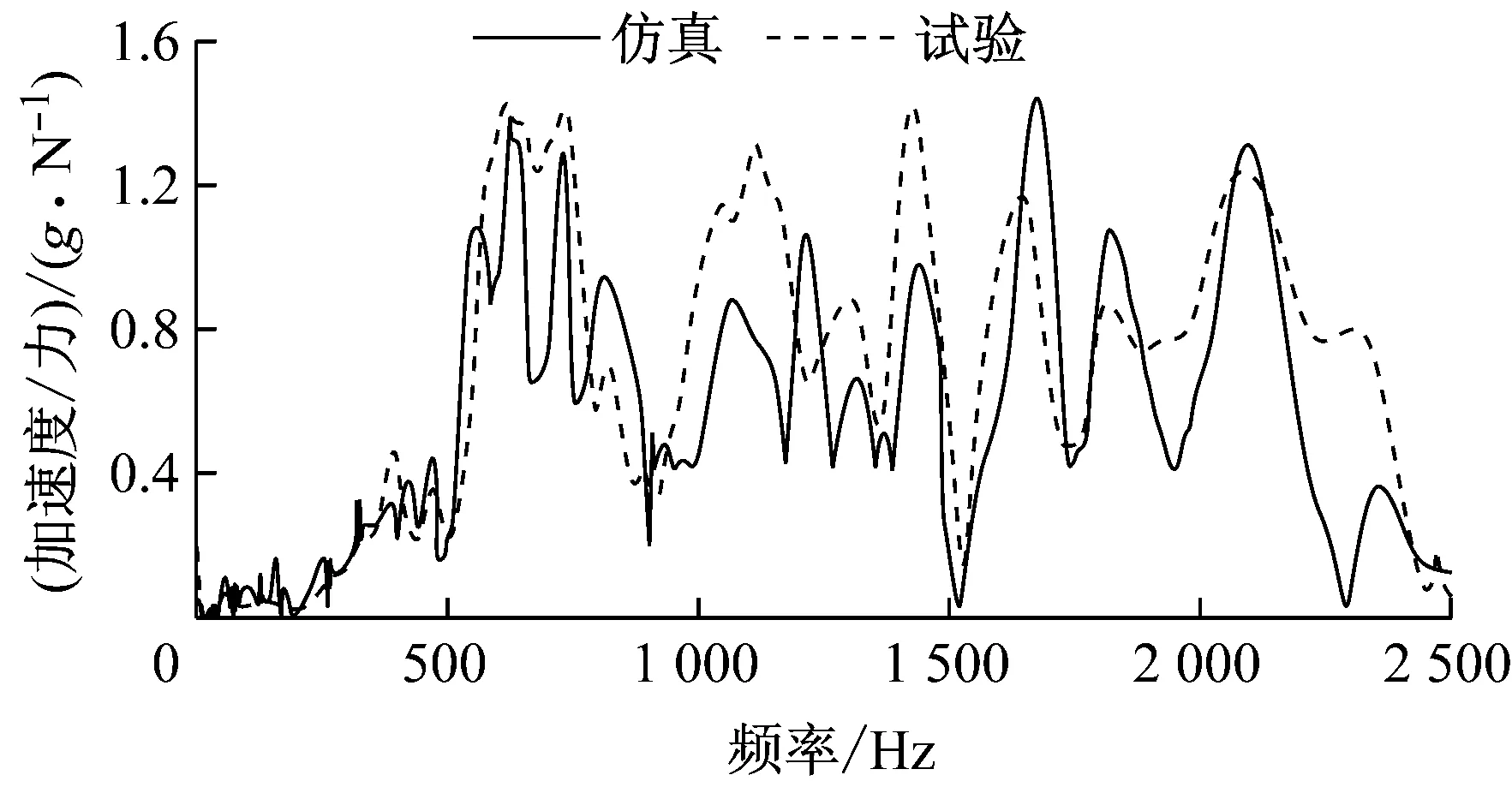
b 测点13图8 侧窗玻璃测点频响函数试验与仿真结果对比

Fig.8Comparisonofsimulatedandtestedfrequencyresponsefunctionsoftestpointsofsidewindowglass

谱密度来表征压力脉动.压力脉动自功率谱密度与互功率谱密度的计算公式如下：

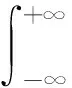
(2)

(3)

式中：ω为圆频率;E为期望函数;p(t)为t时刻的压力分布;ξ1、ξ2分别为两点在x方向与y方向上的距离；p1、p2分别为两点的压力.

侧窗表面压力脉动随时间的变化复杂，且不同位置处的变化也不相同，因此直接使用上述公式计算功率谱密度比较困难.

Corcos在1967年首次建立了经典的湍流边界层压力脉动功率谱密度模型.该模型是一种半经验公式，可通过几个方便测量的空气动力学参数，预估压力脉动功率谱密度.在Corcos模型中，重点关注的参数为频率、自功率谱密度与互功率谱密度.为了使模型描述的规律独立于量纲的影响，对模型中的重要参数进行归一化处理.分别取参考频率和参考功率谱密度为

(4)

(5)

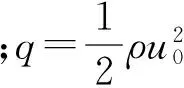
(6)

(7)

Corcos通过拟合试验数据，得到归一化自功率谱密度与互功率谱密度的半经验公式为

(8)

(9)

(10)

(11)

式中：α，β为两个指数系数，通过与试验结果的拟合，它们的取值分别为0.10和0.77[4];uc为局部对流速度.

综上可知，利用Corcos模型，只需要自由流线速度u0，边界层位移厚度δ*以及对流速度uc，便可近似计算得到自功率谱密度与互功率谱密度.

将该功率谱密度作为激励，施加到侧窗等效模型上，并建立声学网格，计算车内部人耳处噪声.由于只考虑左前侧窗振动辐射的噪声，故只建立了车内1/4体积的声学网格，如图9所示.利用有限元仿真方法计算得到车内驾驶员人耳处的声辐射，如图10所示.

图9 车内声学网格Fig.9 Interior acoustic grid

图10 车内驾驶员人耳处的声辐射仿真结果Fig.10 Sound radiation simulated in driver’s ear position

3 试验验证

为验证利用侧窗玻璃系统等效简化模型与Corcos模型计算风激励下汽车侧窗振动辐射噪声的适用性，本文进行激光测振试验，直接获得侧窗表面振动速度分布，并基于该试验数据应用边界元方法(BEM)计算驾驶员人耳处的声辐射.

3.1 激光测振

针对试验车前侧窗玻璃，应用德国Polytec公司激光测振仪，基于多普勒效应，在整车气动声学风洞中测量120 km·h-1风速下，玻璃表面的振动速度分布.

图11为激光测振仪对试验车前侧窗玻璃进行测点振动速度扫描示意图.其中左侧为参考激光头，用来测取参考相位信息，右侧扫描头扫描侧窗玻璃测点位置，逐点采集振动速度信号.

图11 激光测振仪测点扫描示意图

Fig.11Vibrationvelocityscanningoftestpointswithlaservibrometer

在前侧窗玻璃表面布置34个振动速度测点，测点位置与模态试验测点位置相同.测振仪采样时间为15 s，采样频率7.812 5 kHz.同时为降低试验误差，每个测点进行15次试验取平均值，使速度曲线趋于平滑.测量结束后，获得34个测点的振动速度频谱曲线.

3.2 车内声辐射计算(半仿真)

将侧窗振动速度分布作为输入条件计算驾驶员人耳处的声辐射.首先应用振动测点的空间分布建立声学边界元网格，导入测试所得34个测点振动速度频谱，通过边界元法(BEM)计算辐射到驾驶员人耳处的声压级曲线.根据边界元网格尺寸可得分析截止频率约为600 Hz.图12显示的即为车内声辐射的半仿真(基于试验数据)计算结果.

3.3 车内声辐射计算结果对比

如图13所示，将基于Corcos模型应用有限元仿真得到的车内声辐射与基于激光测振仪所测数据进行边界元仿真所得结果(半仿真)进行对比，可以发现，在0～200 Hz范围内，仿真声压级高于半仿真的结果，这可能是由于作为流体激励源的Corcos模型本身在低频段的能量输入偏高造成[11]；在较高频段，两个结果的频谱特性基本吻合.两结果对比说明基于Corcos模型作为激励源计算车内声辐射方法具有一定程度的适用性.

图12 车内驾驶员人耳处的边界元声辐射半仿真结果

Fig.12Soundradiationindriver’searpositionsimulatedwithBEMbasedontestdata(semi-simulation)

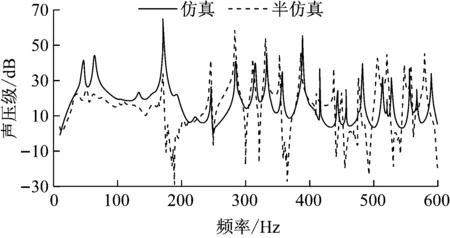
图13 基于仿真与半仿真车内声辐射计算结果对比

Fig.13Comparisonofinteriorsoundradiationbasedonsimulationandsemi-simulationresults

4 结论

(1)针对侧窗密封条复杂的力学性能以及非规则的形状，基于等效原理，将密封条等效成弹簧约束，从而实现了车窗密封系统的离散化等效建模.

(2)通过基于遗传算法的Matlab-Abaqus联合仿真平台可以较准确地拟合弹簧刚度.对比仿真结果与试验数据，发现两种方法的固有频率、振型及频响函数吻合良好，验证了通过等效弹簧进行车窗密封系统离散化建模的合理性及有效性.

(3)利用Corcos模型半经验公式，可以近似计算得到湍流压力的功率谱密度，从而计算流体激励侧窗玻璃振动引起的车内声辐射.通过对比仿真与半仿真计算结果，证明了利用玻璃边界约束等效简化模型与Corcos模型计算风激励下汽车侧窗玻璃振动引起车内声辐射的计算方法具有一定程度的适用性.

参考文献:

[1] TUNCER A, ANLAS G, YILMAZ Y. An investigation of the effect of weatherstrip seals on vehicle vibration and acoustics using an alternative modeling technique [J]. Journal of Vibration and Acoustics, 2014, 136(4): 041018.

[2] DIKMEN E, BASDOGAN I. Material characteristics of a vehicle door seal and its effect on vehicle vibrations [J]. Vehicle System Dynamics, 2008, 46(11): 975.

[3] 朱文峰, 林佩剑, 周辉, 等. 基于非线性刚度拟合的车窗系统约束分析与建模[J]. 机械工程学报, 2015, 51(20): 171.

ZHU Wenfeng, LIN Peijian, ZHOU Hui,etal. Constraint analysis and modeling of automotive window based on nonlinear stiffness fitting [J]. Journal of Mechanical Engineering, 2015, 51(20): 171.

[4] CONEY W B, HER J Y. Characterization of the wind noise loading of production automobile greenhouse surfaces[J]. Fluid-Structure Interaction, Aeroelasticity, Flow-Induced Vibration and Noise, ASME， 1997, 53(1):411.

[5] HAN F, BERNHARD R J. Prediction of flow-induced structural vibration and sound radiation using energy flow analysis[J]. Journal of Vibration and Acoustics, 1999,277(4)：685.

[6] OLSSON A K. Finite element procedures in modelling the dynamic properties of rubber [M]. Lund: Lund University, 2007.

[7] 潘孝勇. 橡胶隔振器动态特性计算与建模方法的研究 [D]. 杭州: 浙江工业大学, 2009.

PAN Xiaoyong. An investigation on calculation and modeling methods for dynamic properties of a rubber isolator [D]. Hangzhou: Zhejiang University of Technology, 2009.

[9] KURMA S. Vibration and stability of composite panels with geometrical discontinuities [D]. Rourkela: National Institutes of Technology, 2013.

[10] 曹金凤, 王旭春, 孔亮. Python 语言在 Abaqus 中的应用[J]. 北京: 机械工业出版社, 2011.

CAO Jinfeng, WANG Xuchun, KONG Liang. The application of Python language in Abaqus [M]. Beijing: China Machine Press, 2011.

[11] CAIAZZO A, D’AMICO R, DESMAT W. A generalized Corcos model for modelling turbulent boundary layer wall pressure fluctuations[J]. Journal of Sound and Vibration, 2016(372):192.