冲击波和预制破片复合作用下H型钢柱损伤效应分析

田 力, 张 浩

(1. 天津大学 建筑工程学院， 天津 300072； 2. 天津大学 滨海土木工程结构与安全教育部重点实验室， 天津 300072)

近年来，世界各地恐怖袭击事件、局部战争和爆炸事故频发，以往暴恐袭击目标主要针对军事及政府建筑，近年来逐渐转向普通民用建筑.钢结构在民用建筑中应用日益广泛，且主要应用于大型公共标志性建筑，而钢柱作为钢结构的主要承重构件，其抗爆能力直接关系着整个结构的抗爆水平.一旦发生爆炸破坏，会引起钢结构的连续性倒塌，将造成严重的人员伤亡和恶劣的社会影响.因此研究钢柱的抗爆能力具有重要的现实意义.

冲击波和破片作为爆炸对结构的主要毁伤因素，以往研究人员主要是将其解耦成2个问题分别予以研究.Liew和Chen[1-2]研究了爆炸冲击波作用下不同柱长、加载方式和边界条件对钢柱动力响应的影响；李忠献等[3]考虑应变率效应和损伤累计效应，分析了钢柱在爆炸冲击波作用下的动力响应及破坏模式；黄燕玲等[4]利用AUTODYN研究了直径为8 mm的圆柱形破片侵彻钢板时穿透深度的变化规律；赵强等[5]研究了破片群对不同结构混凝土板的侵彻效应；姜鹏飞等[6]分析了高速破片群对装配式钢板-混凝土组合结构的侵彻效应，指出其破坏模式为整体破坏.近年来研究人员逐渐认识到二者复合作用对结构的毁伤具有叠加增强效应[7-9].由于问题的复杂性，目前对于钢柱在爆炸冲击波和预制破片复合作用下的研究基本处于空白状态.鉴于钢柱构件的重要性，展开对钢柱在爆炸冲击波和预制破片复合作用下的研究迫在眉睫.

本文基于非线性有限元软件ANSYS/LS-DYNA，模拟了H型钢柱在近距爆炸冲击波和预制破片复合作用下的损伤破坏，分析了冲击波载荷、破片群载荷及复合载荷作用下钢柱的变形和破坏特征，运用参数化分析方法研究了轴压比、钢材强度、长细比和截面类型等因素对钢柱在近距爆炸冲击波和预制破片复合作用下损伤效应的影响.

1 有限元模型及数值分析方法

1.1 模型简介

为分析热轧H型钢柱在近距爆炸冲击波和预制破片复合作用下的损伤效应，本文建立了如图1,2所示的计算模型.H型钢截面尺寸为300 mm×300 mm×15 mm×10 mm×13 mm(腹板宽度×翼缘宽度×腹板厚度×翼缘厚度×圆角半径)[10]，柱高3 000 mm.为准确模拟钢柱的边界条件，在计算模型中建立了柱头和柱脚[11]，柱头柱脚高度均为150 mm，柱脚水平方向位移和竖直方向位移均被约束，柱头只约束水平方向位移.在柱头上端施加均布面荷载，以准确模拟实际工况中的竖向荷载.竖向荷载F=0.2Fp，其中Fp=4 800 kN,是钢柱的极限承载力，其数值依据详见4.1节.炸药采用圆柱形TNT炸药，半径为80 mm，高度为160 mm，距刚性地面300 mm，爆距为500 mm，采用中心起爆方式.通过在炸药柱身外贴预制破片来模拟爆炸冲击波和破片的复合作用.单个破片厚度为8 mm，高为10 mm，对应的圆心角为5°.由于近距爆炸产生破坏效应的局部性，考虑时间效率，借鉴文献[12]的作法，将空气域的尺寸取为800 mm×1 240 mm×480 mm，对空气设定无反射透射边界.为准确模拟破片群作用区钢柱的破坏，对由空气包围的钢柱进行网格加密.空气单元网格尺寸为8 mm，炸药单元网格尺寸为4 mm，钢柱加密区网格尺寸为4 mm，非加密区网格尺寸为8 mm,破片单元网格尺寸为10 mm.网格划分后，炸药和空气域单元数约为63万个，钢柱单元数约为23万个，破片总数为1 152个.

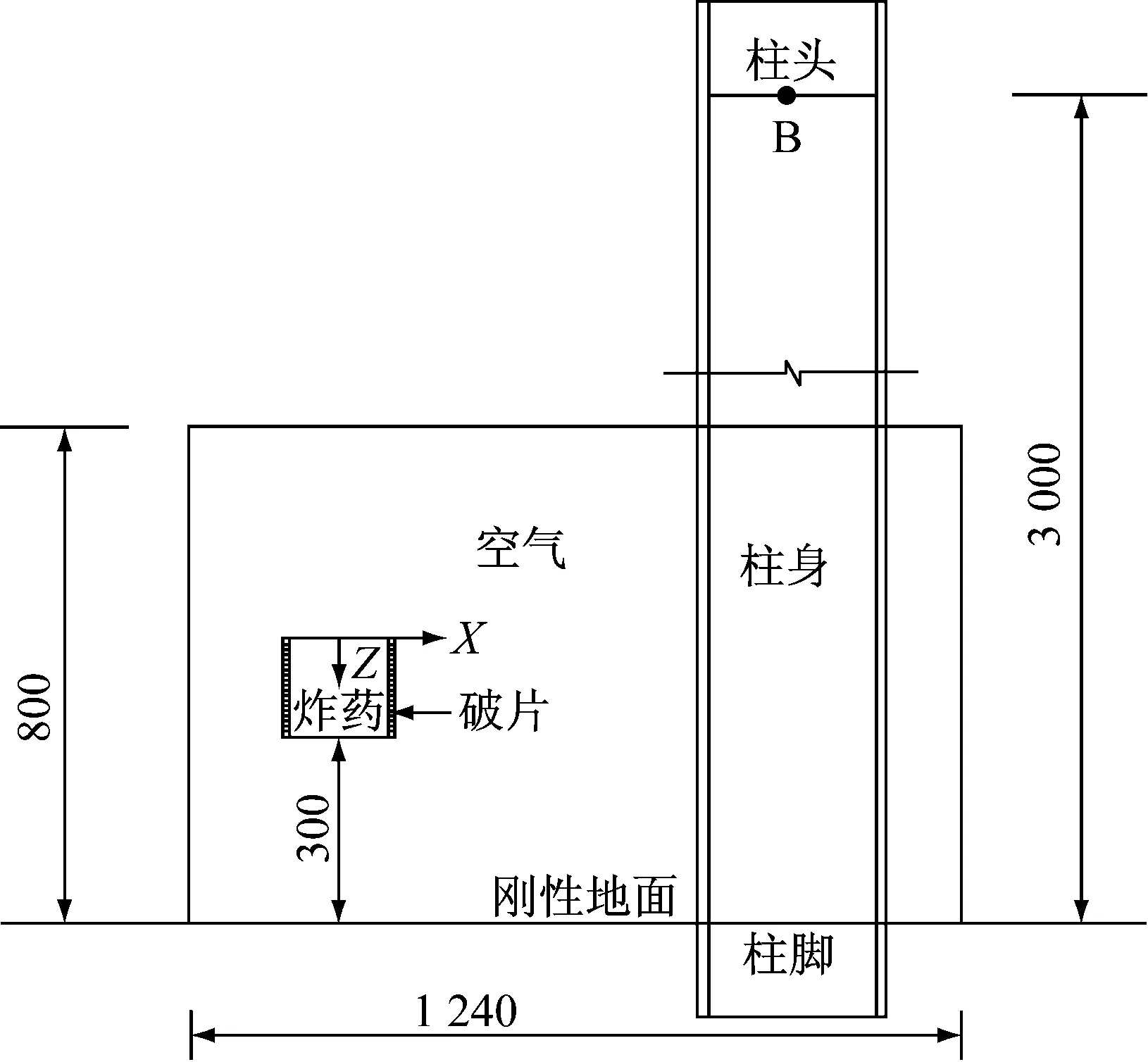
a 正视图

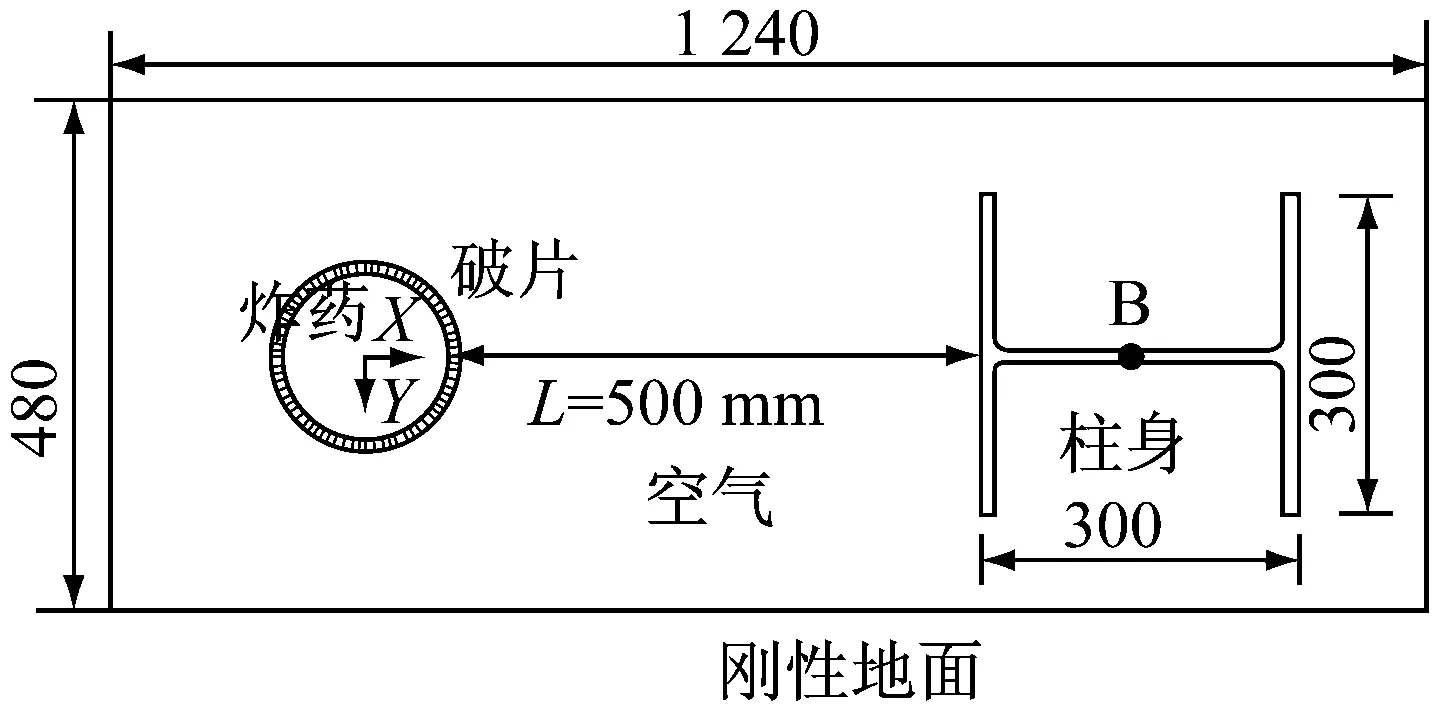
b 俯视图图1 模型示意图(单位：mm)Fig.1 Schematic diagram of the model(unit: mm)

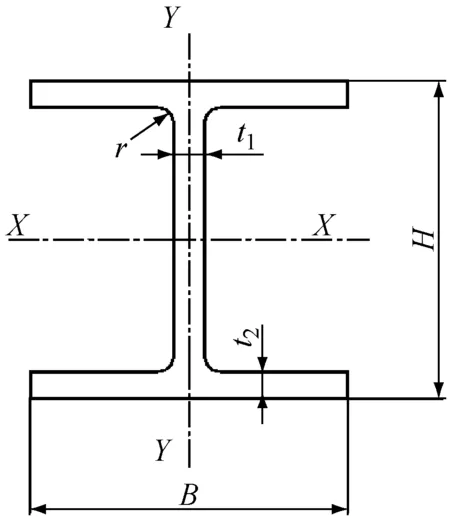
H为腹板宽度；B为翼缘宽度；t1为腹板厚度；t2为翼缘厚度；r为圆角半径

图2H型钢截面示意图

Fig.2SchematicdiagramofH-sectionsteel

1.2 数值分析方法

数值模型由炸药、破片、空气、钢柱和刚性地面5部分组成.除刚性地面外均采用三维实体单元Solid164模拟，刚性地面采用关键字*RIGID_WALL_PLANER模拟.对破片和钢柱单元采用Language算法模拟，炸药和空气单元采用ALE算法模拟.采用罚函数耦合算法模拟钢柱和破片与空气和炸药之间的流固耦合.破片和钢柱之间的接触定义为侵蚀接触；破片之间、破片和刚性地面之间采用自动单面接触，设置接触刚度缩放因子为1.0.由于高速碰撞会在材料内部产生应力波，因此在分析中将人工体积黏性加进压力项.设置线性黏性系数和二次项黏性系数为0.06和1.00[13].时间步长比例因子取为0.67.为了控制采用单点积分带来的沙漏模态，采用刚性沙漏控制，沙漏系数取0.03.

1.3 本构模型

TNT炸药采用*MAT_HIGH_EXPLOSIVE_BURN本构模型及JWL状态方程描述.

式中：A、B为材料常数；R1、R2、ω为试验拟合参数；E0为单位体积的初始内能；V为相对体积.炸药和状态方程参数见表1.

空气采用*MAT_NULL本构模型及*EOS_LINEAR_POLYNOMIAL状态方程描述.

PA=C0+C1u+C2u2+C3u3+

(C4+C5u+C6u2)E0

式中：C0、C1、C2、C3、C4、C5、C6均为常数；E0为单位体积的初始内能；V为相对体积.具体参数详见表2.

钢柱采用JOHNSON_COOK本构模型，该模型考虑了钢材的应变硬化效应、应变率效应和温度软化效应.文献[14]指出将破片当成刚体是一种可行的方式，因此本文忽略了预制破片在爆轰过程和侵彻过程中的变形和损伤，将破片视为刚体，选用*MAT_RIGID材料模型描述.

式中：σy为钢材动态屈服强度；E为静态屈服强度；F为应变硬化模量；n为应变硬化指数;C为应变率系数；m为热软化指数；ε0为参考塑性应变；εp为有效塑性应变；T为材料温度；Tm为材料的熔点；T0为参考温度(取室温).具体参数见表3.

为避免大变形引起的单元畸变，在有限元模拟中往往引入失效准则，与JOHNSON_COOK本构模型相对应的JOHNSON_COOK失效准则可描述为

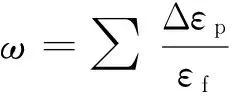
表1 炸药参数Tab.1 Material properties of TNT

表2 空气参数Tab.2 Material properties of air

表3 钢材参数Tab.3 Material properties of steel

2 仿真方法验证

由于目前缺乏关于钢柱在爆炸冲击波和预制破片复合作用下的试验，因此本文分别对装药驱动金属平板、爆炸冲击波对钢板作用、复合载荷对钢板作用进行了数值模拟，以验证耦合算法、接触类型和本构模型的合理性.

2.1 装药驱动金属平板飞散速度验证

在装药设计一面为金属平板结构，一面为自由面时，国内外一直沿用了格尼提出的计算破片初始速度的公式[15].其计算公式为

W=ρMπD2hM/12

hM=(D/2){1+[1+(d/2h)2]-0.5}

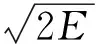
在实际爆轰过程中，对于圆柱形装药驱动平板运动，文献[15]指出真正用来驱动平板运动的装药质量并不是整个圆柱形装药，当装药高度大于装药直径时，用来驱动平板运动的炸药为装药高度等于装药直径的正圆锥体的质量.因此公式中W为实际驱动破片的炸药质量.

本文对装药驱动金属平板进行了数值模拟(图3).金属平板直径为50 mm，厚度为2 mm.最终仿真结果为：金属平板飞散速度为2 660 m·s-1，比理论公式中得到的计算结果2 673 m·s-1小0.5%.从仿真结果看，本文采用的仿真模型参数能够较准确地模拟装药驱动金属平板的飞散速度.

图3 装药驱动金属平板模型图Fig.3 Schematic diagram of charge-drivenmetal plate model

2.2 近距空爆载荷下钢板动态响应验证

陈长海等[16]对近距空爆载荷作用下固支方板的变形和破坏模式进行了试验研究.本文选取文献中典型试验工况2进行仿真计算,以验证爆炸冲击波单独作用下钢板动态响应的准确性.

验证模型尺寸与文献[16]中试验工况2相同，钢板边界条件为四边固支，空气边界为无反射透射边界.接触类型、耦合算法及本构模型均采用1.2和1.3节所述.固支钢板中心点在t=1.1 ms左右达到最大挠度，随后在平衡位置附近小幅震荡，其最终稳定值约为42.8 mm(图4)，与文献[16]试验中平板中心处的最大挠度值42.3 mm相差1.2%.可见，数值模拟结果具有较高的准确性.

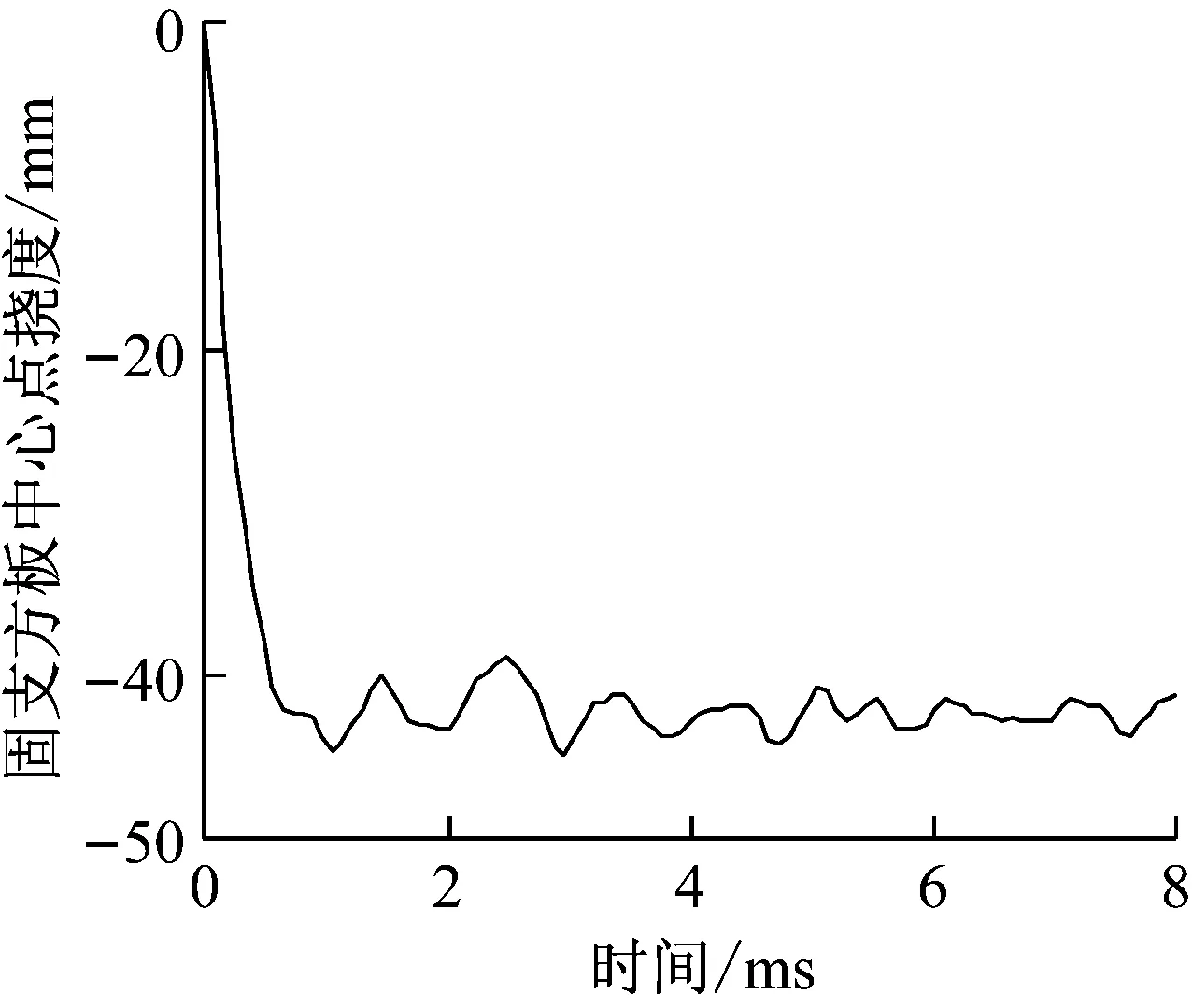
图4 钢板中心点位移时程曲线Fig.4 Displacement history curves of plat center point

2.3 爆炸冲击波和破片复合作用下钢板变形破坏验证

张成亮[17]进行了爆炸冲击波和预制破片复合作用下固支方板的变形和破坏模式试验研究.试验中固支方板平面尺寸为700 mm×700 mm，除去方板固定的边界部分，实际载荷作用面积为500 mm×500 mm，钢板厚4 mm，装药为圆柱形铸装TNT炸药，位于固支方板的中心处，炸药底部距离钢板上表面距离为148 mm.炸药直径50 mm，单发装药高度为65 mm,采用2发叠加布置，单发质量为200 g，于装药顶端引爆.预制破片由Q235钢板线切割加工而成.单块预制破片尺寸为5 mm×5 mm×2 mm，破片数共计89个.试验装置见图5.

图5 试验装置Fig.5 Diagram of test device

数值模型由钢板、炸药、破片和空气组成，均采用三维实体Solid164单元.其中钢板、炸药和破片模型尺寸和试验中相同.模型布置如图6所示.为更加准确模拟破片群密集作用区钢板的破坏，对钢板中心区域160 mm×160 mm的方形区域进行网格细化.空气单元尺寸5 mm，炸药单元尺寸1 mm，破片单元尺寸2 mm,钢板加密区单元尺寸2 mm,非加密区4 mm.模型单元数共计约80万个.边界条件为四边固支.接触类型、耦合算法及本构模型均采用1.2和1.3节所述.

图6 复合作用计算模型Fig.6 Diagram of combined load

图7和图8为试验结果和仿真结果对比图.从图8中可以看出：固支方板中心处充塞破口直径模拟值为43.86 mm，与试验值43.00 mm吻合；试验中破口边沿由多个直径约为7 mm的穿甲弹孔连接而成,与模拟结果直径约为10 mm极为相似.试验中固支方板产生了整体挠曲大变形，破口附近区域产生塑性变形，出现最大挠度25.0 mm[17].仿真模型中得到破口附近的最大挠度值为27.8 mm，与试验值相当.破片着靶位置距破口中心的最大距离为155 mm，与模拟值184 mm相差较大.考虑到试验中炸药位置不能正对钢板中心、破片布置的非对称以及破片飞散的发散性(前期较小的误差因破片发散飞行导致后期误差较大),且周遭破片对钢板的损害程度较小，因此此数据产生的误差可以忽略不计.通过以上分析可见，本文采用的数值模型能够较好地模拟爆炸冲击波和破片复合作用下对钢板的变形破坏.

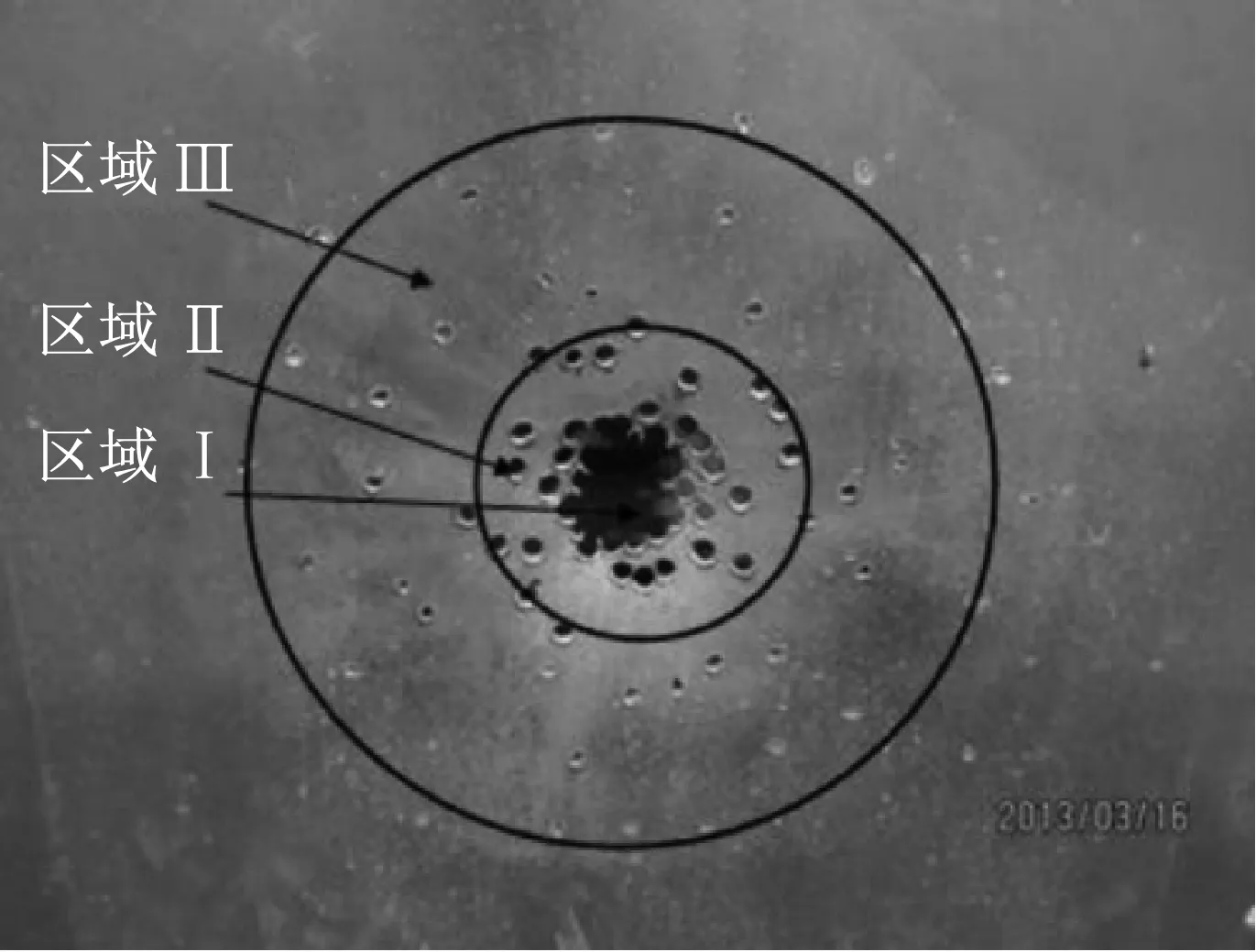
图7 试验结果Fig.7 Experiments results of the steel plate

a 俯视图

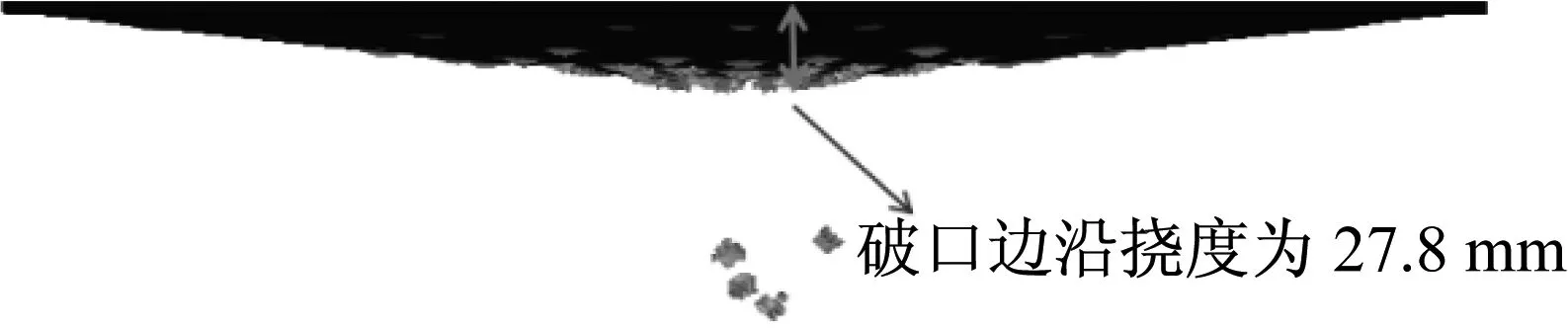
b 侧视图图8 仿真结果Fig.8 Numerical results of steel plate

3 冲击波作用、破片群作用及复合载荷作用下H型钢柱损伤效应的对比

表4给出了4种数值模拟工况(其中Model-4并未进行真实的数值模拟)，以探究冲击波作用、破片群作用及复合载荷作用下H型钢柱前翼缘A—A处(图9)动态响应的异同.

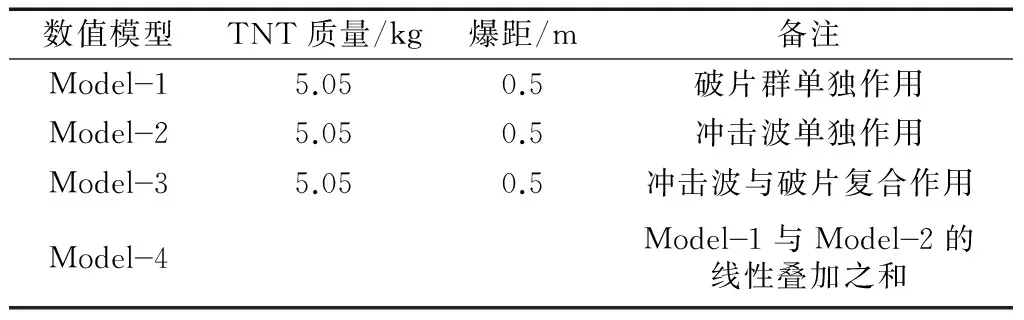
表4 数值模拟工况Tab.4 Conditions of numerical models

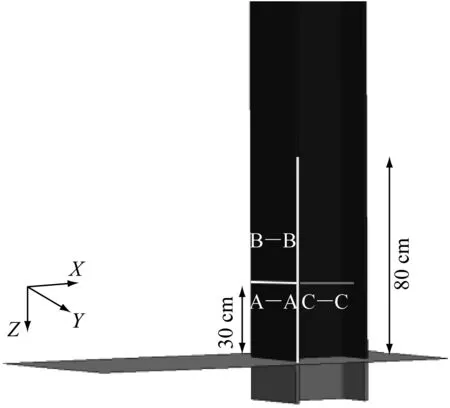
图9 位置示意Fig.9 Schematic diagram of location

3.1 复合毁伤载荷分析

Model-1中，破片约在t=0.34 ms时到达钢柱；Model-2中，钢柱约在t=0.12 ms时开始受到冲击波载荷的作用，t=0.15 ms时达到超压峰值55.6 MPa；Model-3中，钢柱约在t=0.31 ms时开始受到冲击波载荷的作用，t=0.33 ms时达到超压峰值36.5 MPa.可以看出：在冲击波和破片群复合作用下，钢柱首先受到冲击波的作用，而后受到破片群的冲击作用.冲击波正压持续作用时间为0.11 ms，大于冲击波和破片群到达的时间间隔0.03 ms，因此两者对结构的作用将产生耦合效应；因破片数量设置较大，有一部分冲击波用来驱动破片飞散，且冲击波遇到破片时发生反射和绕流现象，导致Model-3冲击波到达的时间出现了延迟,超压峰值出现了减弱.所以破片的存在对冲击波的传播过程影响很大.

3.2 位移响应分析

图10为钢柱前翼缘A—A处X向位移峰值图，图11为钢柱塑性应变云图.由于钢柱破坏的局部性，为更加清楚直观地表现破坏形态，故只截取了产生塑性应变的钢柱部分.由图11可知：Model-1中钢柱受破片群作用时整体并无大的挠曲变形，破片群的破坏作用主要体现在撞击凹坑和破片穿孔；Model-2中钢柱受爆炸冲击波的作用产生了挠曲大变形，且其变形曲线更加平滑，其最大变形值为35.57 mm，在柱脚及翼缘和腹板连接处出现了塑性变形；Model-3中在爆炸冲击波和破片群复合作用下产生了更大的变形，其最大挠度值为49.80 mm.和Moldel-1相比，前翼缘产生了更大的塑性变形，因冲击波的存在改变了破片群的运行轨迹，导致Model-3后翼缘破坏程度较低.Model-4位移峰值均小于Model-3，说明复合载荷作用比二者单独作用的线性叠加破坏还要严重.通过以上分析可知：冲击波和破片群的破坏机理不同，冲击波主要引起钢柱的挠曲变形，而破片群主要为局部侵蚀作用.复合载荷破坏作用具有叠加增强效应.

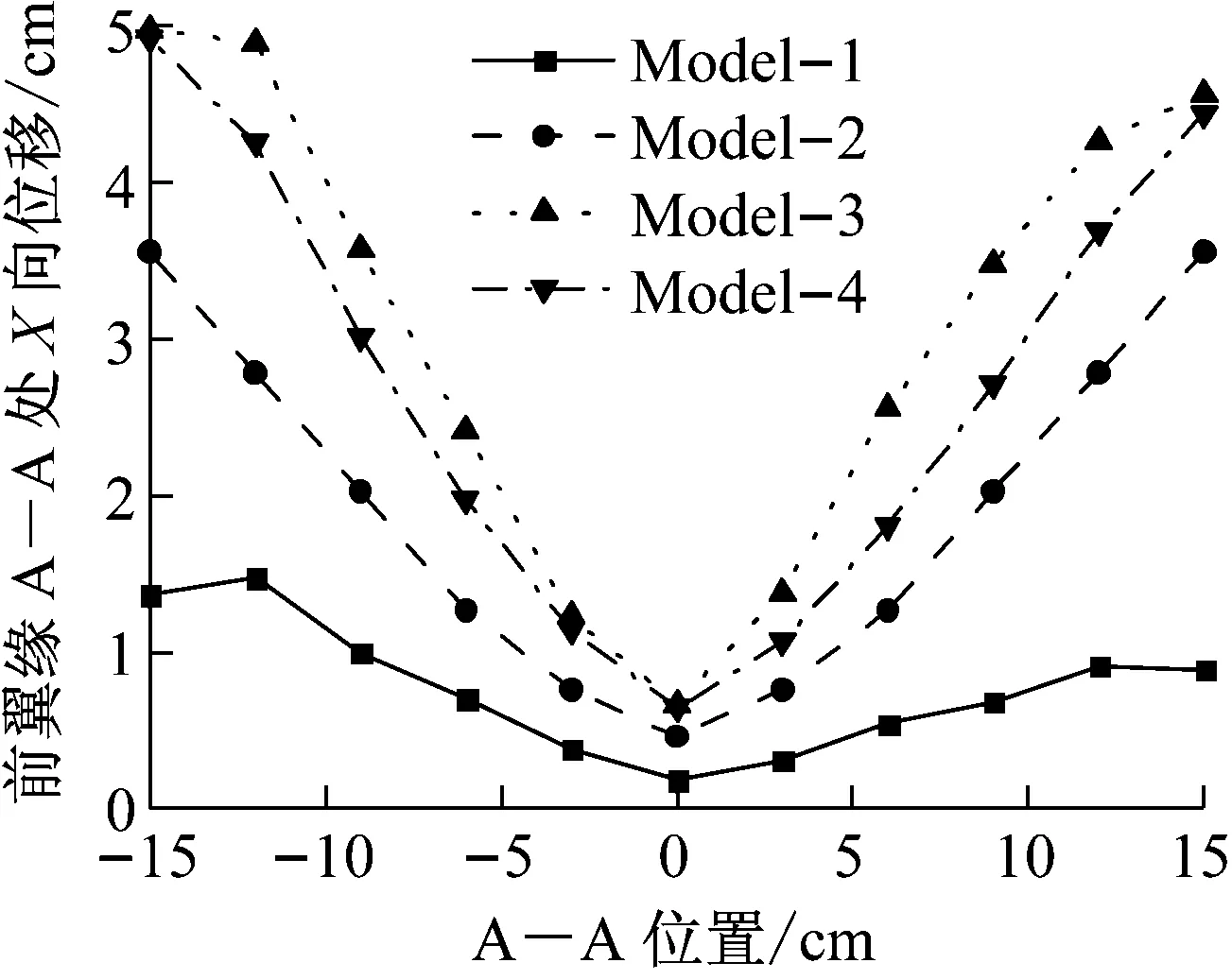
图10 钢柱前翼缘A—A处X向位移峰值Fig.10 X-direction deformation profile offront flange A—A of steel column

3.3 能量分析

图12为钢柱动能和内能时程曲线.由图12可以看出：破片群单独作用时钢柱动能峰值为21.8 kJ，是冲击波单独作用时钢柱动能峰值6.7 kJ的3倍多，复合载荷时的的动能峰值35.0 kJ仍大于二者单独作用的线性之和28.5 kJ.再次说明破坏作用具有叠加增强效应.图12b中冲击波单独作用时钢柱内能远远小于破片群单独作用时钢柱内能296.0 kJ和复合载荷作用时钢柱内能224.0 kJ，因此在抗爆防护设计时应考虑破片的作用，且其应作为防护设计的主要设计荷载.复合载荷作用时钢柱获得的内能小于破片群单独作用时钢柱获得的内能,原因为复合载荷作用时，由于冲击波先作用于结构，导致预制破片侵彻钢柱之前结构已经处于较高的应力水平，破片群更加容易穿透钢柱，导致钢柱获得的内能较低.

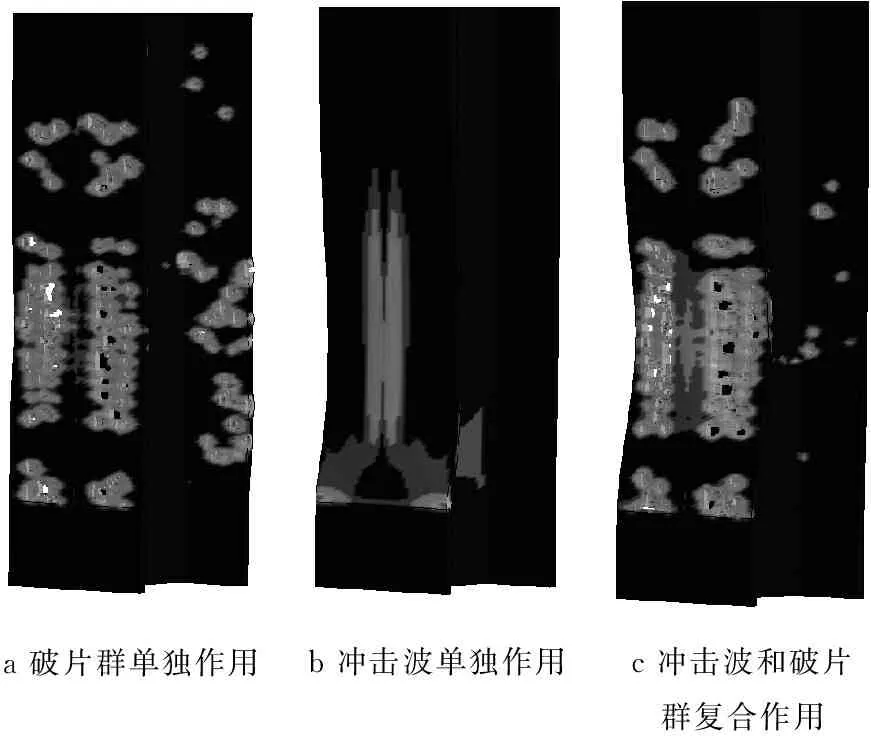
a破片群单独作用b冲击波单独作用c冲击波和破片群复合作用

图11不同荷载作用下钢柱塑性应变云图

Fig.11Plasticstraincloudsofsteel

columnsatdifferentloads

a 钢柱动能

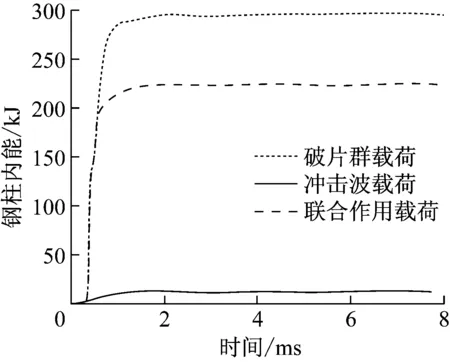
b 钢柱内能图12 钢柱动能和内能时程曲线Fig.12 Time-history curve of steel columnkinetic energy and internal energy

4 冲击波与破片群复合作用下H型钢柱损伤效应的参数化分析

4.1 轴压比

在实际工程结构中，钢柱是主要的竖向承重构件.柱子承受的轴向压力F和柱的轴心受压稳定承载力Fp的比值为轴压比n.为研究不同轴向压力对钢柱抗爆性能的影响，本小节分析了轴压比分别为0、0.2、0.4、0.6、0.8时钢柱的损伤效应.

为确定钢柱的轴心受压稳定承载力Fp，建立钢柱竖向承载模型.在柱顶缓慢施加轴向荷载，通过跟踪柱顶点竖向位移时程曲线以确定钢柱的极限破坏状态，从而得出钢柱的竖向极限承载力.图13所示为柱顶点竖向位移时程曲线.根据时程曲线曲率变化情况，判断柱子的竖向极限承载力Fp=4 800 kN.

图14所示为不同轴压比下钢柱塑性应变云图.由图14可知：当轴压比不大于0.4时，钢柱产生了挠曲变形和破片穿孔，并未发生倒塌破坏，仍具有一定的承载能力.当轴压比为0.6、0.8时，钢柱均因翼缘和腹板产生局部屈曲导致钢柱不能继续承载而发生倒塌破坏.随着轴压比的增大，破片破坏作用由撞击凹坑变为破片穿孔，甚至破口边界撕裂连通形成更大的破口.破口直径和数量逐渐变大.

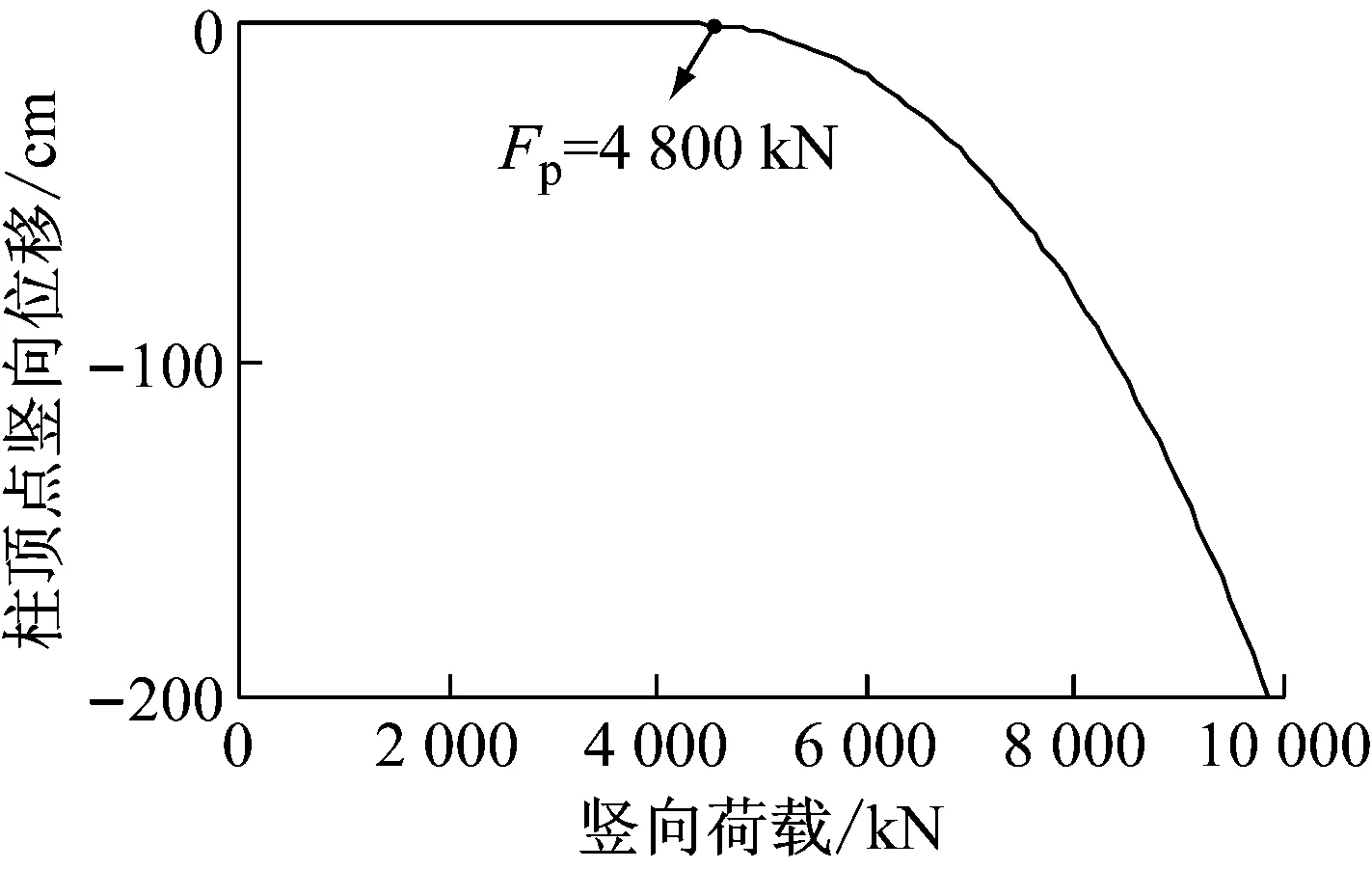
图13 柱顶点竖向位移时程曲线Fig.13 Time-history curve of vertical displacement

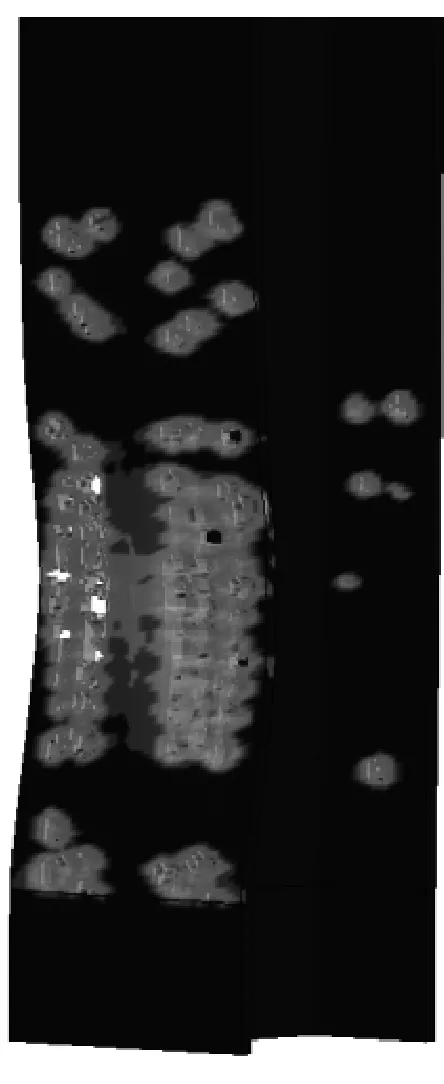
a n=0

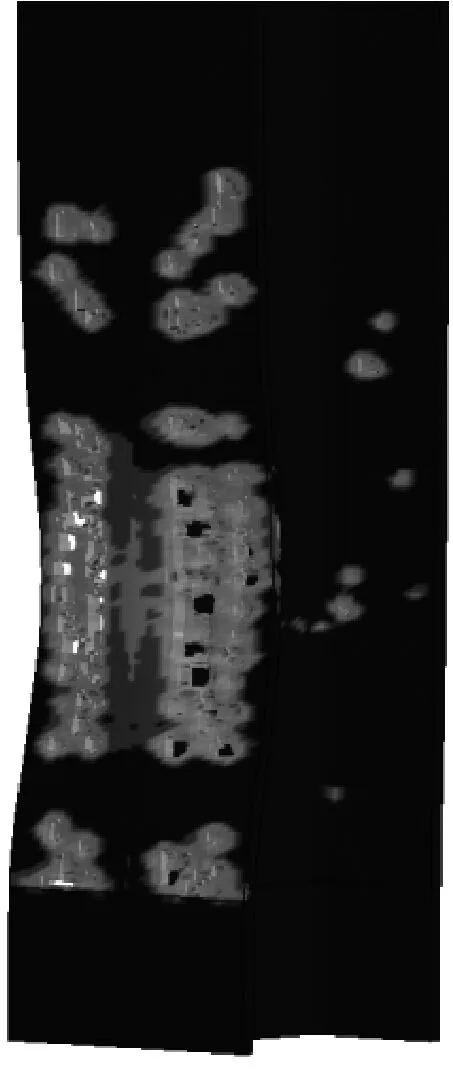
b n=0.2

c n=0.4

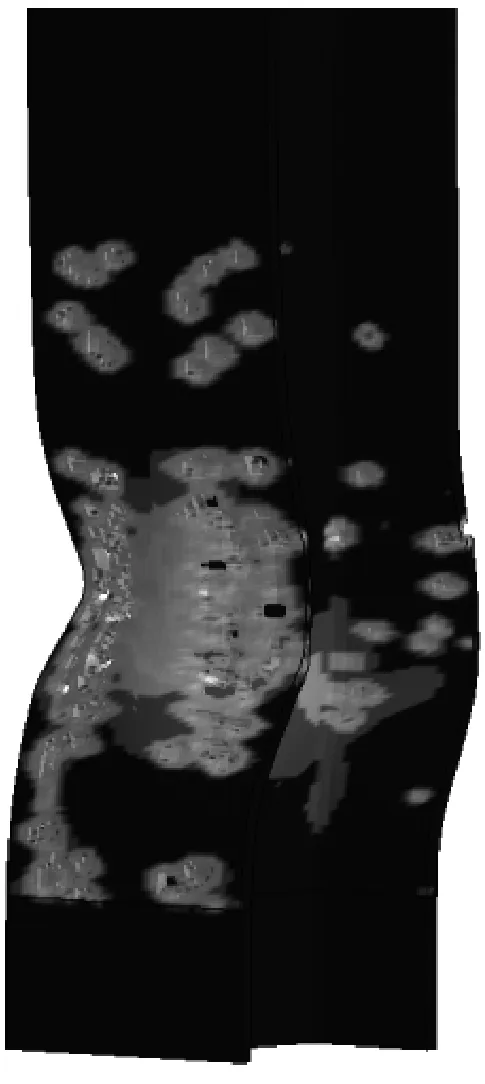
d n=0.6

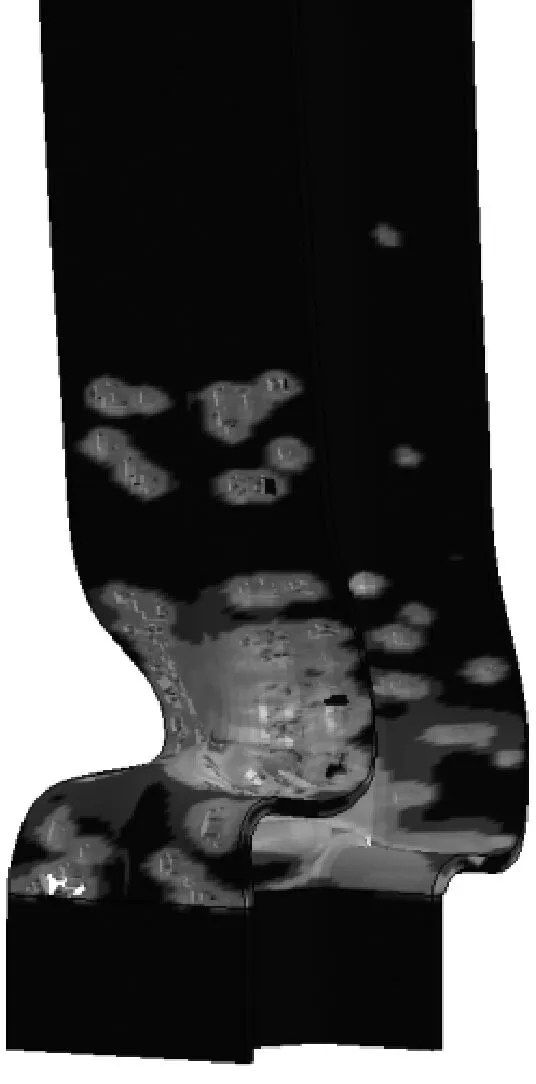
e n=0.8图14 不同轴压比下钢柱塑性应变云图Fig.14 Plastic strain diagram of steel column at different axial compression ratios

图15为钢柱在不同轴压比下前翼缘A—A处、B—B处及腹板C—C处位移峰值(示意位置见图9).从图15中可以看出：对于H型钢柱前翼缘A—A处及B—B 处位移峰值，随着轴压比的增大，前翼缘及腹板变形程度呈现非线性增加.轴压比不大于0.4时，前翼缘及腹板变形轮廓相近.当轴压比继续增大时，变形迅速增大.由H型钢柱腹板C—C处位移峰值可见，轴压比小于0.4时，腹板只在一侧产生了微小的屈曲变形，当轴压比超过0.4后，腹板两侧均产生了屈曲变形，且变形幅度很大.因此在钢柱的抗爆设计中，应控制其所承受的轴向压力大小.钢材强度等级为Q235时，轴压比不宜大于0.4.

4.2 钢材强度

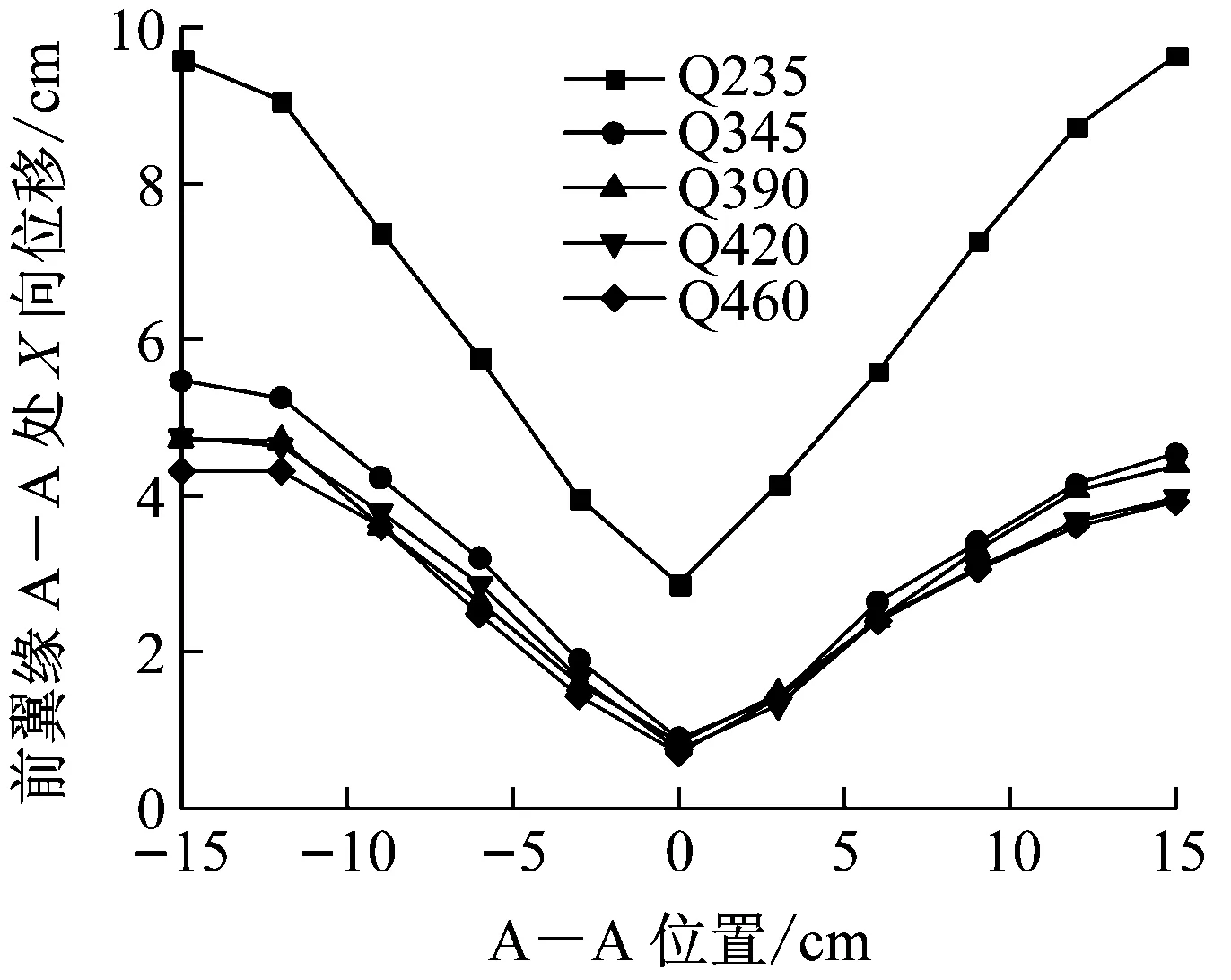
为探究爆炸冲击波和预制破片复合作用下，不同钢材强度等级对H型钢柱损伤效应的影响,保持钢柱截面类型和尺寸不变，柱高均为3 m.为了更好地观察钢柱变形情况的差异，轴向压力选取轴压比为0.6时所施加的压力F=2 880 kN.本文模拟了钢材强度等级分别为Q235、Q345、Q390、Q420和Q460时钢柱的损伤效应.图16为不同钢材强度等级钢柱前翼缘A—A处、B—B处及腹板C—C处位移峰值(示意位置见图9).

由图16可知：对于H型钢柱前翼缘A—A处及B—B处位移峰值，钢材强度从Q235提高到Q345，其变形大幅减小.随着钢材强度继续增大，其变形程度基本不变.对于H型钢柱腹板C—C处位移峰值，钢材强度为Q235时，腹板两侧均产生了较大的屈曲变形，其他强度等级钢材只在腹板一侧产生了屈曲变形，且变形幅度较小，尤其对于Q390以上钢材，其腹板屈曲变形基本接近.

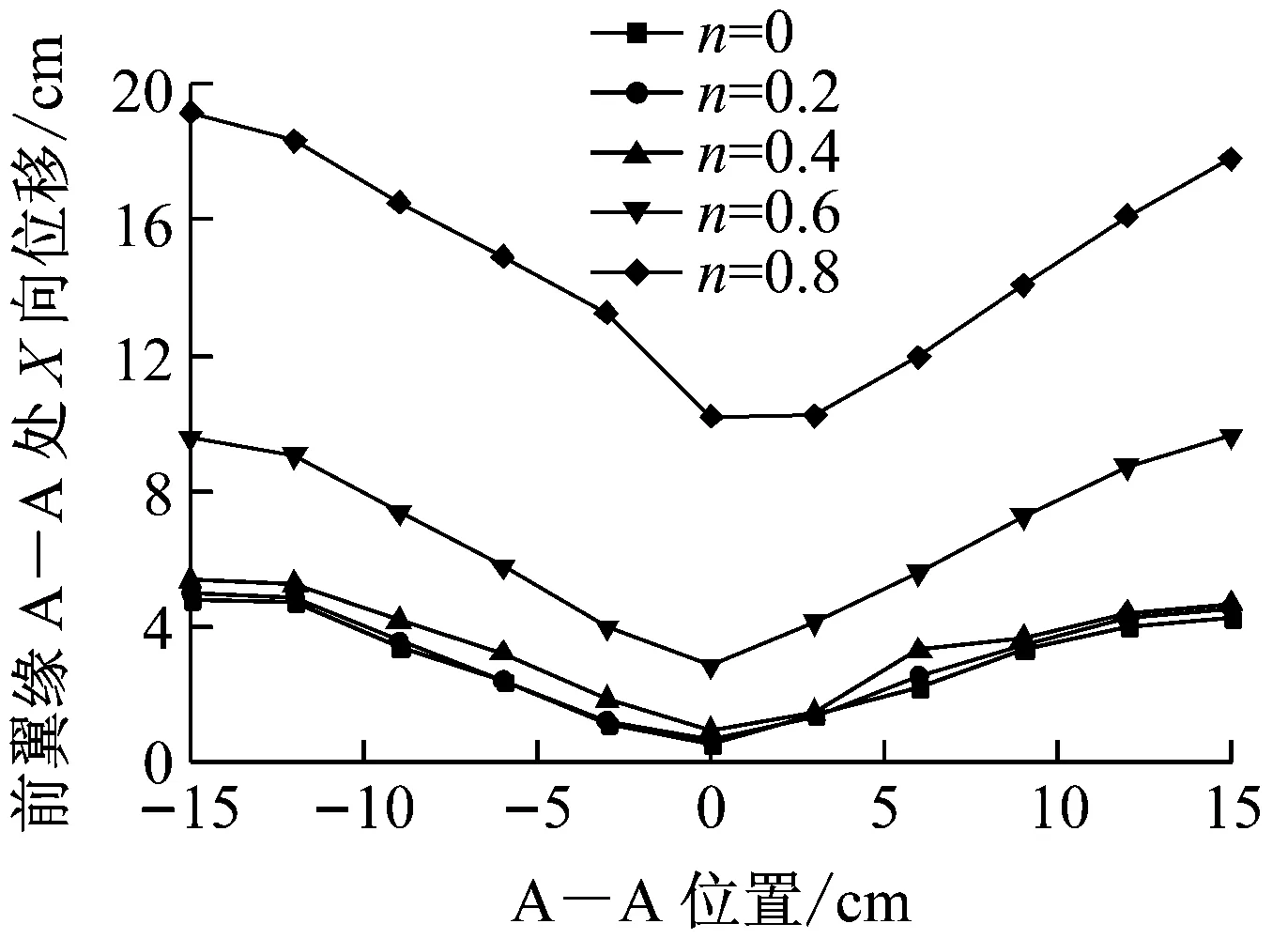
a 前翼缘A—A处X向位移峰值

b 前翼缘B—B处X向位移峰值

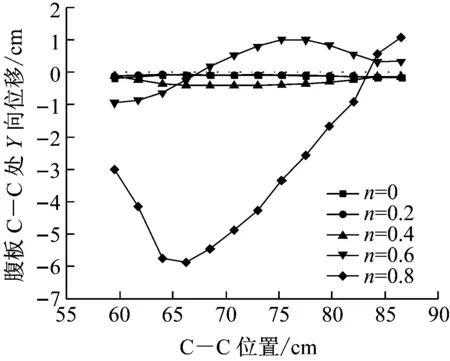
c 腹板C—C处Y向位移峰值图15 不同轴压比下钢柱变形位移峰值

Fig.15Deformationdisplacementdiagramofsteelcolumnatdifferentaxialcompressionratios

a 前翼缘A—A处X向位移峰值

b 前翼缘B—B处X向位移峰值

c 腹板C—C处Y向位移峰值图16 不同钢材强度钢柱位移峰值

Fig.16Deformationanddisplacementdiagramofsteelcolumnswithdifferentsteelstrengths

4.3 长细比

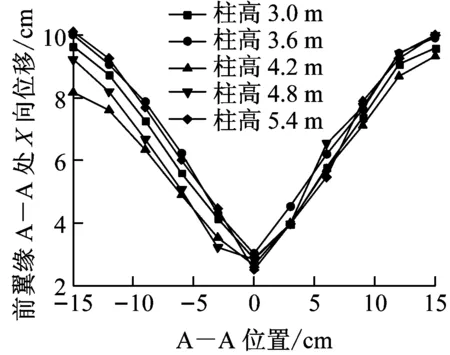
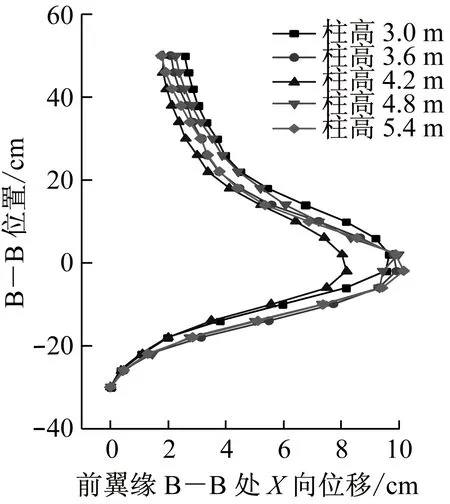
为研究长细比对H型钢柱在爆炸冲击波和预制破片复合作用下抗爆性能的影响，保持钢柱截面类型和尺寸不变，钢材强度等级均为Q235，轴向压力F=2 880 kN.通过改变柱高来实现长细比的变化.选取柱高分别为3.0、3.6、4.2、4.8和5.4 m的H型钢柱进行数值模拟.图17为钢柱在不同柱高下前翼缘A—A处、B—B处及腹板C—C处位移峰值(示意位置见图9).

由图17H型钢柱前翼缘A—A处及B—B处位移峰值可知，随着柱高的改变，其变形轮廓和程度基本接近，相差不大.由图17中H型钢柱腹板C—C处位移峰值可知，柱高为3.0 m时，由于腹板两侧均产生了屈曲变形，其单侧变形幅度相对较小一些.其他柱高均在腹板单侧产生了较大的屈曲变形.

结果表明：由于炸药距离地面和钢柱较近及爆炸作用的瞬时性，破坏作用更多地呈现出局部性.因此通过改变柱高来减小长细比对钢柱抗爆能力没有实质性的改善.

4.4 截面类型

为探究不同截面类型对钢柱在爆炸冲击波和预制破片复合作用下抗爆性能的影响，保持钢柱截面面积不变，即总用钢量不变，选取H型截面、箱形截面、圆管型截面3种截面类型进行数值模拟.柱高均为3.0 m，钢材强度等级为Q235，轴向压力F=2 880 kN.

a 前翼缘A—A处X向位移峰值

b 前翼缘B—B处X向位移峰值

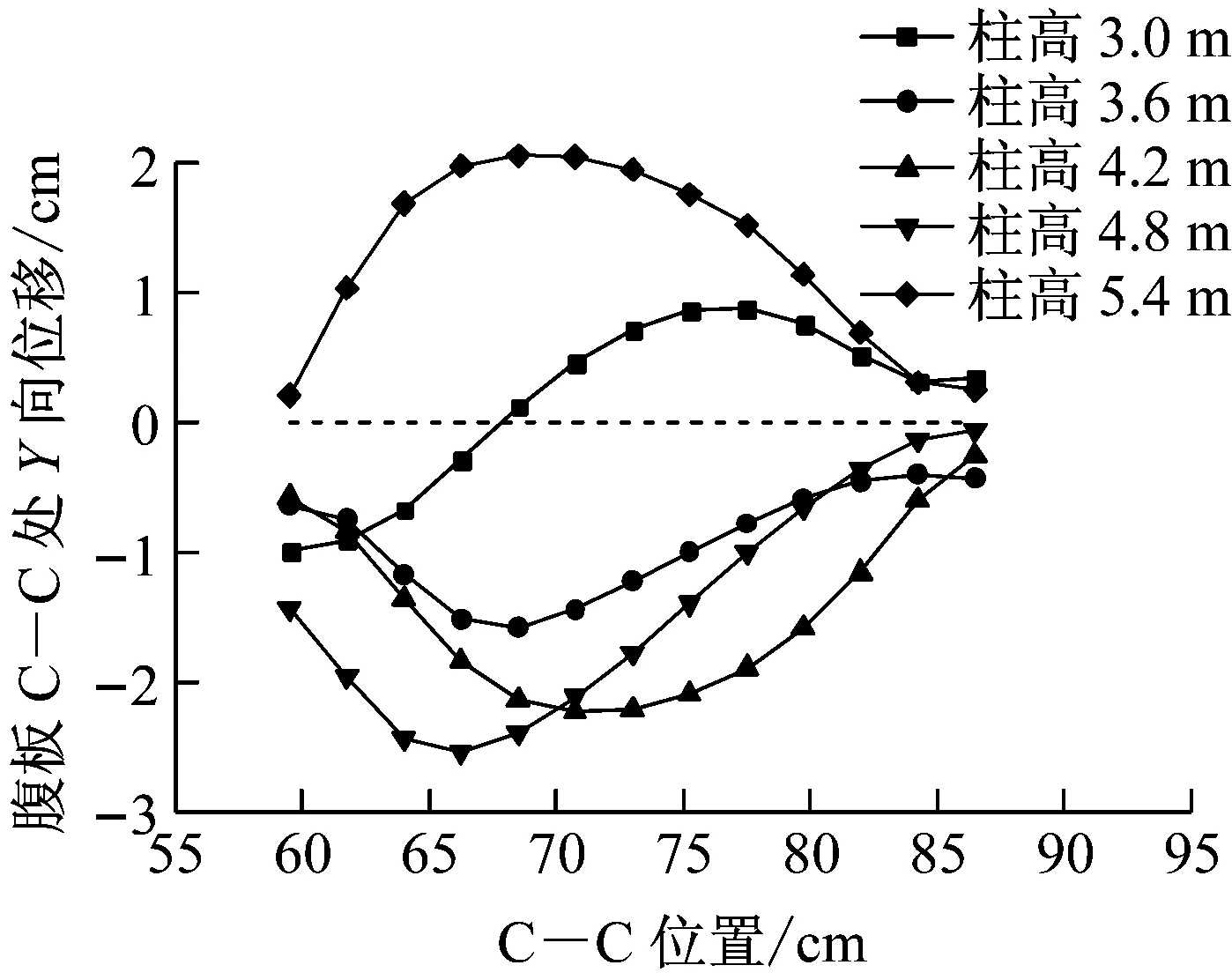
c 腹板C—C处Y向位移峰值图17 不同柱高钢柱位移峰值Fig.17 Displacement and displacement diagram of different column high steel columns

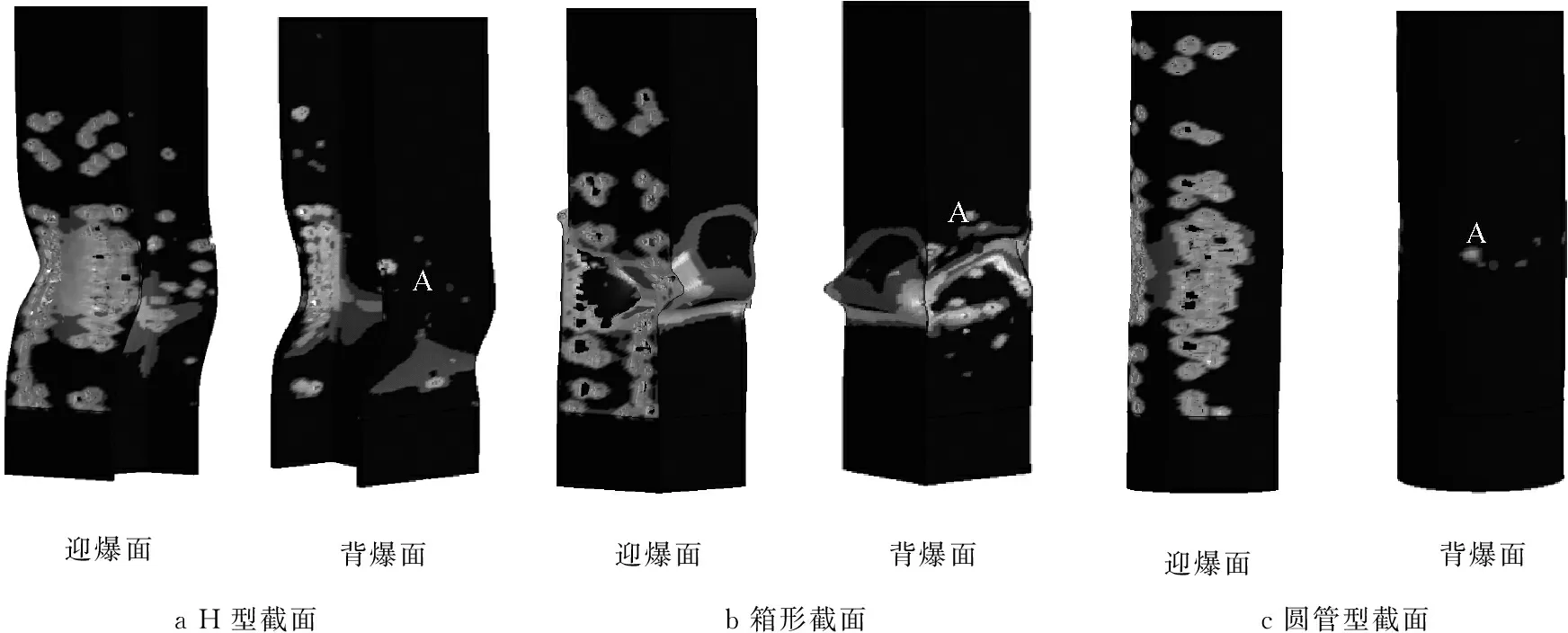
图18所示为不同截面类型钢柱塑性应变云图.由图18可知：H型截面钢柱迎爆面产生了较大屈曲变形，表面有一定数量的撞击凹坑和破片穿孔，背爆面同样产生了屈曲变形，背爆面内侧有撞击凹坑，但未形成破片穿孔.箱形截面迎爆面产生了大面积破口，两侧腹板及背爆面产生了严重的屈曲变形，背爆面内侧同样存在撞击凹坑.圆管型截面迎爆面表面有显著的撞击凹坑和破片穿孔，但其屈曲变形并不是很大，背爆面几乎没有发生破坏.

迎爆面背爆面迎爆面背爆面迎爆面背爆面aH型截面b箱形截面c圆管型截面

图18不同截面类型钢柱塑性应变云图

Fig.18Plasticstraindiagramofsteelcolumnofdifferentcross-sectiontypesteels

图19为柱A点(见图18)X向位移时程曲线.由图19可知：圆管型截面钢柱的水平位移最小，H型截面和箱形截面均产生了很大的水平位移，箱形截面背爆面上A点首先是向外凸出，故其位移在开始时迅速增大，且其增长速率明显大于H型截面，随着时间推移，箱形柱承载能力逐渐下降，背爆面发生了向内凹陷(见图18)，故其A点X向位移在t=2.8 ms时发生了下降，且出现了负数，证明向内凹陷程度很大.

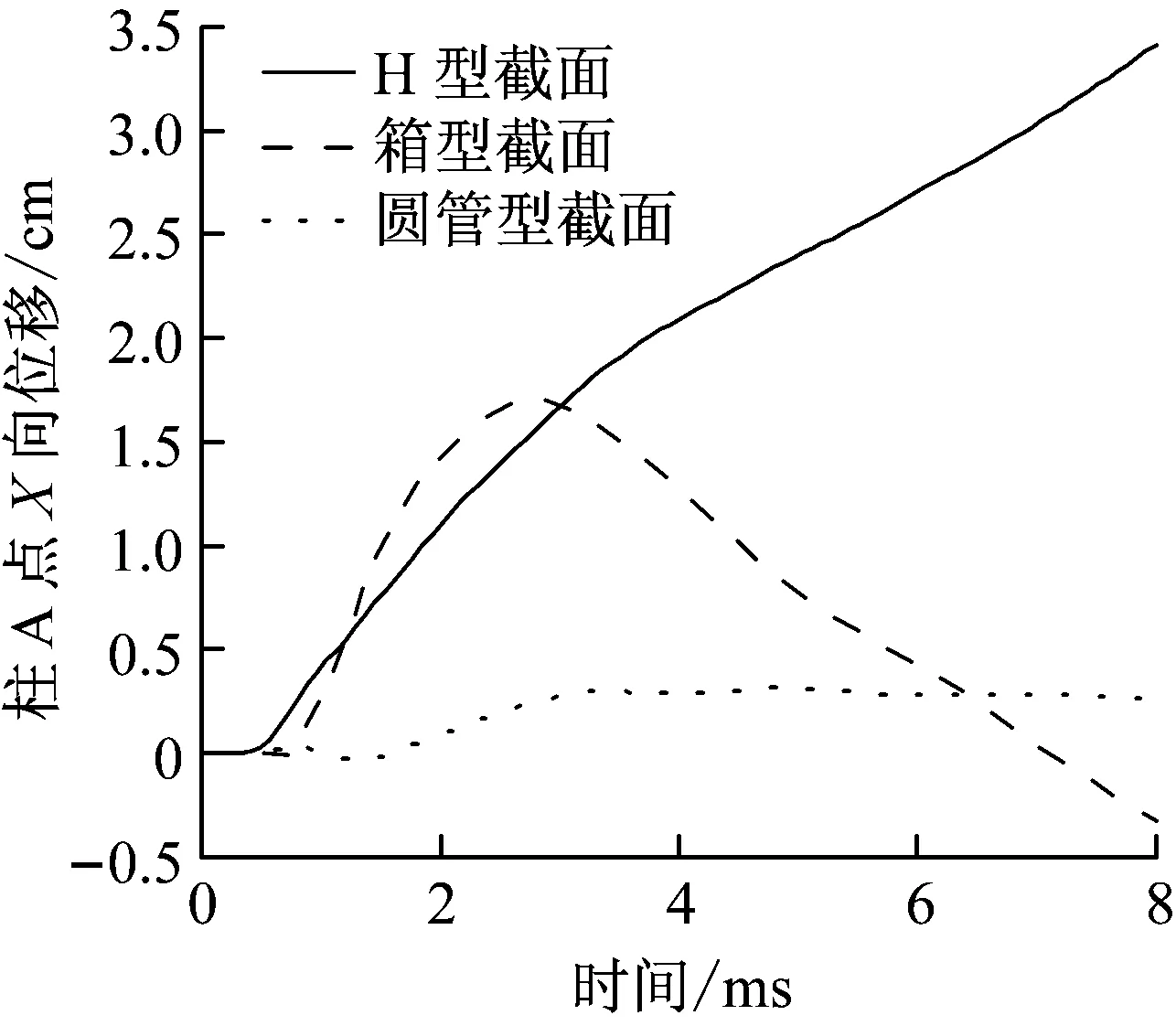
图19 柱A点X向位移峰值Fig.19 Horizontal displacement of column A point

图20为柱顶B点(见图1)Z向位移图，可以看出：圆管型截面钢柱柱顶B点竖向位移最小且逐渐趋于平稳，证明其没有发生屈曲失稳破坏.箱型截面和H型截面钢柱顶点位移均逐渐增大，证明其发生了屈曲失稳破坏，且箱形截面破坏速率和程度更加严重.

河北省文化厅高度重视“三区”人才支持计划文化工作者专项工作，2013年国家级财政及河北省级财政共拨付项目专款69.8万元，2014年拨付资金56.54万元，2015年拨付资金43.28万元，2016年拨付资金43.28万元，共计212.9万元，足额资金的保障，为项目的顺利开展奠定了必要的基础。

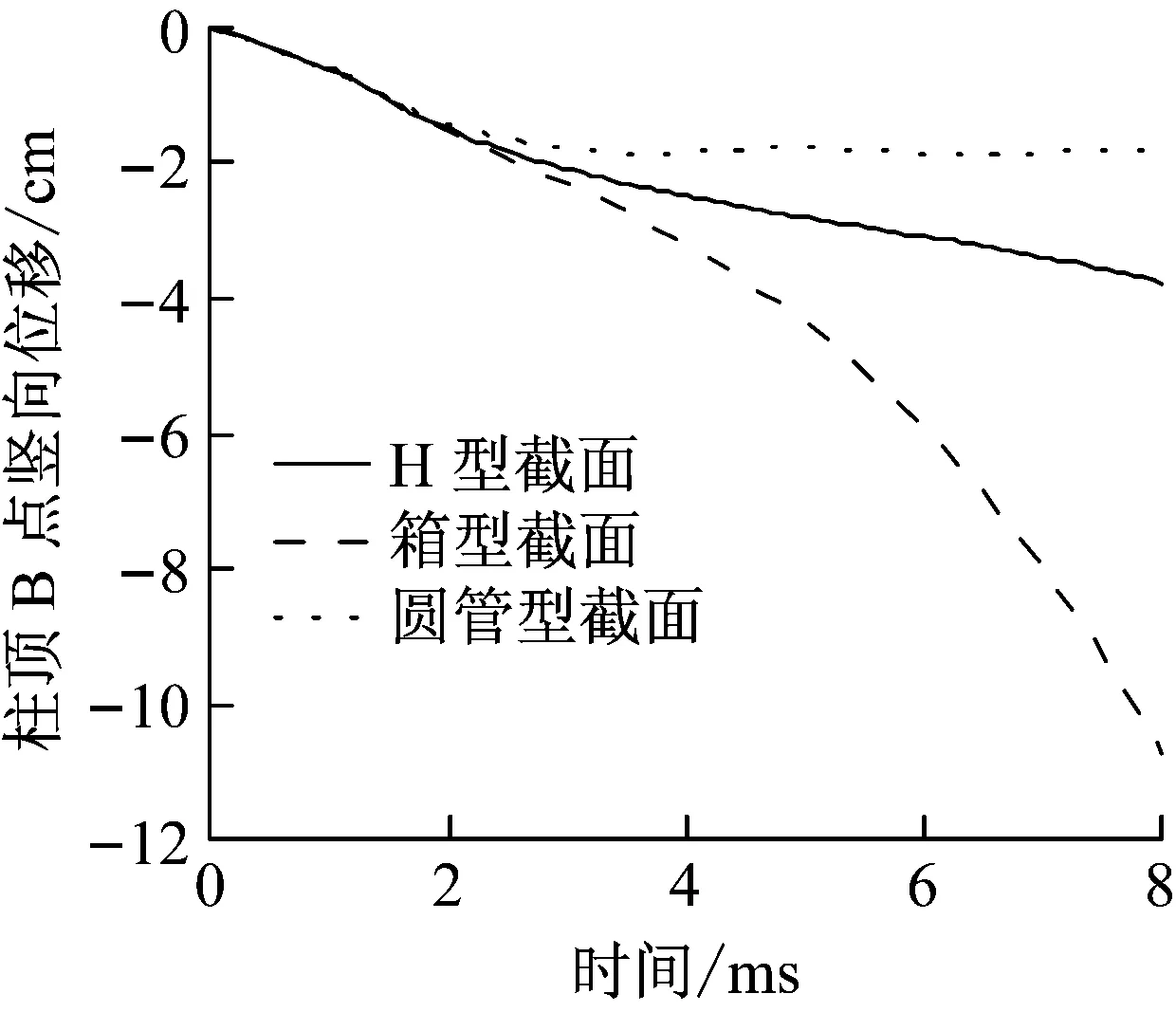
图20 柱顶B点Z向位移时程Fig.20 Vertical displacement of steel colume

结果表明：在近距爆炸冲击波和预制破片复合作用下，在相同用钢量下，圆管截面的抗爆能力最好，H型截面次之，箱形截面最差.

5 结论

本文通过在炸药柱身外贴预制破片来模拟爆炸产生的冲击波和破片复合作用对H型钢柱损伤效应的影响，利用有限元软件ANSYS/LS-DYNA分析了冲击波单独作用、破片群单独作用及复合载荷作用下钢柱损伤效应的差异.研究了轴压比、钢材强度、长细比和截面类型等因素对钢柱破坏效果的影响，得出如下主要结论：

(1)冲击波和破片群的破坏机理不同，冲击波主要引起钢柱的挠曲变形，而破片群主要为局部侵蚀作用.破坏作用具有叠加增强效应.复合载荷作用比二者单独作用的线性叠加破坏还要严重.

(2)在近爆复合载荷作用下，钢柱首先受到冲击波的作用，而后受到破片群的冲击作用.两者对结构的作用将产生耦合效应；由于有一部分冲击波用来驱动破片飞散，且冲击波遇到破片时发生反射和绕流现象,导致冲击波到达的时间出现了延迟,超压峰值出现了减弱，故破片的存在对冲击波的传播过程影响很大.

(3)冲击波单独作用时钢柱内能远远小于破片群单独作用时钢柱内能，因此在抗爆防护设计时应考虑破片的作用，且其应作为防护设计的主要设计荷载.

(4)在H型钢柱抗爆设计中，应控制其所承受的轴向压力大小，钢材强度等级为Q235时，轴压比不宜大于0.4.应合理选择钢材强度等级，而不应盲目选择高强度钢材.通过改变柱高来改变长细比对钢柱抗爆能力的提高作用不大.在相同用钢量下，圆管型截面钢柱的抗爆能力最好，H型截面次之，箱形截面最差.

参考文献:

[1] LIEW J Y R, CHEN H.Explosion and fire analysis of steel frames using fiber element approach [J]. Journal of Engineering, 2004, 130(7):991.

[2] CHEN H, LIEW J Y R.Explosion and fire analysis of steel frames using mixed element approach [J]. Journal of Engineering, 2005, 131(6):606.

[3] 李忠献，刘志侠，丁阳.爆炸荷载作用下钢结构的动力响应和破坏模式[J].建筑结构学报，2008,29(4)：106.

LI Zhongxian,LIU Zhixia,DING Yang.Dynamatic response and failure modes of steel structures under explosive loading[J]. Journal of Building Structures, 2008, 29(4):106.

[4] 黄燕玲，吴卫国，李晓彬，等．圆柱形破片侵彻靶板的数值计算研究[J]．兵器材料科学与工程，2010，33(1)：35.

HUANG Yanling,WU Weiguo,LI Xiaobin,etal, Numerical study on cylindrical fragment penetrating target[J]. Ordnance Material Science and Engineering, 2010, 33(1):35.

[5] 赵强, 辛凯, 邓亮宇. 多破片对不同结构混凝土板的破坏对比试验研究[C]∥中国土木工程学会防护工程分会暨第九次学术年会论文集.长春：中国土木工程学会，2004：526-531.

ZHAO Qiang, XIN Kai, DENG Liangyu. Experimental study on damage of concrete slabs with different structure comparison of multi fragments[C]∥The Ninth Academic Annual Conference of the Council of Protection Engineering Branch of the Civil Engineering Society of China. Changchun: The Civil Engineering Society of China, 2004: 526-531.

[6] 姜鹏飞, 唐德高, 伍俊. 装配式组合防爆墙抗高速破片侵彻性能研究[J]. 振动与冲击, 2008, 27(7): 131.

JIANG Pengfei, TANG Degao, WU Jun. Analysis on penetration characteristics of assembled blast-resistance wall impacted by fragments with high velocities[J]. Journal of Vibration and Shock, 2008, 27(7): 131.

[7] MARCHAND K A, VARGAS M M, NIXON J D.The synergistic effect of blast and fragments,AD-A260[R].San Antonio：Southwest Research Institute, 1992.

[8] QIAN L, QU M, FENG G. Study on terminal effects of dense fragment cluster impact on armor plate. Part I: analytical model [J]. International Journal of Impact Engineering, 2005,31:755.

[9] QIAN L, QU M. Study on terminal effects of dense fragment cluster impact on armor plate. Part II: numerical simulations [J].International Journal of Impact Engineering,2005,31:769.

[11] 师燕超.爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D].天津：天津大学，2008.

SHI Yanchao. Dynamic response behavior and damage mechanism of reinforced concrete structures under explosive load[D]. Tianjin: Tianjin University，2008.

[12] CHUNG KIM YUEN S,LANGDON G S,NURICK G N,etal.Response of V-shape plates to localized blast load experiments and numerical simulation[J].International Journal of Impact Engineering,2012,46:97.

[13] 尚晓江，苏建宇.ANSYS_LSDYNA动力分析方法与工程实例

[M].北京：中国水利水电出版社，2008.

SHANG Xiaojiang，SU Jianyu. ANSYS_LS-DYNA dynamic analysis method and engineering example[M]. Beijing: China Water Conservancy and Hydropower Press，2008.

[14] 段新峰,呈远胜,张攀，等.冲击波和破片联合作用下Ⅰ型夹层板毁伤仿真[J].中国舰船研究，2015,10(6):45.

DAUN Xinfeng,CHENG Yuansheng,ZHAGN Pan. Damage simulation of type Ⅰ sandwich plate under shock wave and fragment joint action[J]. Chinese Journal of Ship Research, 2015,10(6):45.

[15] 孙业斌. 爆炸作用与装药设计[M]. 北京: 国防工业出版社, 1987.

SUN Yebin. Explosive action and charge design[M]. Beijing: National Defence Industry Press, 1987.

[16] 陈长海,朱锡,侯海量,等.近距空爆载荷作用下固支方板的变形及破坏模式[J].爆炸与冲击,2012,32(4):368.

CHEN Changhai, ZHU Xi, HOU Hailiang,etal. Deformation and failure modes of clamped square plates under close-range air blast loads[J].Explosion and Shock Waves,2012,32(4):368.

[17] 张成亮.爆炸冲击波和高速破片联合作用效应及防护机理研究[D].武汉：海军工程大学，2013.

ZHANG Chengliang. Study on the combined effect and protection mechanism of explosive shock wave and high speed fragmentation[D].Wuhan: Naval Engineering University,2013.

[18] 顾祥林.高应变率下建筑钢筋的本构模型[J].建筑材料学报，2008，11(1)：14.

GU Xianglin. Constitutive models for reinforcing steel bars under high strain rates[J]. Journal of Building Materials,2008，11(1)：14.