基于事件链的平面交叉口右转评估技术
汪 凡, 陈雨人, 王耀东
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
平面交叉口是制约道路通行能力的关键节点,同时也是交通安全风险最高的地方.国内外对于交叉口的评价方法主要是before-after法,根据交叉口设施改进的前后情况的对比,对新的交叉口几何设计或改善措施的有效性进行评价.Tarrall 等[1]采用了before-after分析法,分析左转信号配时改变前后的交叉口内冲突情况,评估信号配时改变的有效性.Sayed 等[2]提出了安全等级的评价方法,描述平均小时冲突数和交通流的指标,将交叉口的安全等级分为了A~F 6个等级.潘福全等[3]将交叉口内的冲突结合几何设计与交通标志的影响,提出了新的安全等级模型.对于交叉口服务水平的评估,通常采用延误、两次停车率、效率指数等指标,反映交叉口的通畅程度.采用交通噪声、大气污染等指标反映服务质量和社会、经济效益.张鹏等[4]采用蒙特卡洛法仿真交叉口的实际运行状态,通过计算交叉口的车均延误来评估通行效率.
上述评估技术,基本采用单一的评估指标,单独评估安全性或者通行效率,缺乏综合的评估方法.事实上,交叉口是一个复杂的系统,几何设计条件、交通流、信号控制等都会引起安全和效率的扰动.对于大型交叉口,通常采用四相位信号配时方案,在时间上将不同方向的车流进行分离.典型的组合方式为:相位1南北直行、相位2南北左转、相位3东西直行、相位4东西左转.此时,右转车辆不受信号控制.对于典型的四相位交叉口,如果交通参与者都能遵守交通信号,则理论上所有的交通冲突都与右转车相关.基于此,对四相位交叉口右转区域进行评估,可在一定程度上反映整个交叉口安全性和效率.
基于事故的交通安全评价方法存在评价周期长、数据获取困难等缺陷,交通冲突是非事故间接评价方法中最常用的技术,冲突的严重程度还反映了交通参与者安全感的大小[5].本文以交通冲突技术作为研究的基础,利用该技术获取基础的试验数据并进行初步评价指标的提取.建立右转事件链模型,详细分析交叉口内右转的冲突事件.引入可靠度,从概率的角度计算事件链的安全性.引入延误,利用排队理论计算交通运行效率.建立交叉口综合性评估方法,对交叉口设计方案与交通流适应性进行解释、预测和改善.
1 右转事件链
在四相位平面交叉口内,将机动车右转看作一个过程以及所经历的不同状态.认为右转机动车在时间和空间上,经历多个阶段和不同种类的冲突和延误.本文将这一过程描述为右转事件链,从机动车开始右转行为直至驶离交叉口,其中每一部分称为事件单元,如图1所示.

a

b
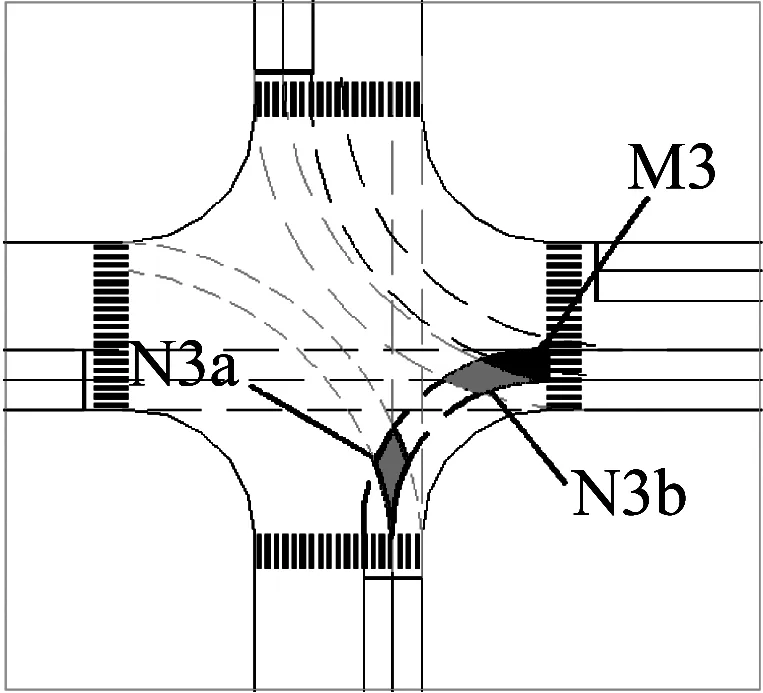
c图1 不同相位下的右转事件链Fig.1 Right-turn event chains in different phases
右转车辆冲突按照冲突参与者可分为:行人P(pedestrian),非机动车N(non-motor)以及机动车M(motor).按照冲突发生的信号相位可分为3类:以从南往东方向的右转车为例,冲突相位包括东西向通行相位(phase 1),南北向通行相位(phase 2)以及南北向左通行相位(phase 3).东西向左转通行相位(phase 4)不影响右转机动车.将机动车右转过程在空间和时间上与机动车、非机动车、行人可能产生冲突的情况划分为8个事件单元.P1、N1、M1分别表示右转机动车与东西向直行行人、非机动车、机动车在相位phase 1段可能发生交通冲突的事件单元(图1a);P2、N2分别表示右转机动车与南北向直行行人、非机动车在相位phase 2段可能发生交通冲突的事件单元(图1b);N3a、N3b、M3分别表示右转机动车与左转非机动车、机动车在相位phase 3阶段可能发生交通冲突的事件单元(图1c).
每一辆在平面交叉口的右转机动车,都将在时间和空间上依序通过事件单元.各事件单元在空间上所占区域大小与交叉口几何设计因素有关(例如交叉口大小、转弯半径、人行道位置等).事件单元冲突与延误的发生与否则直接受到交通环境的影响,例如机动车流量、非机动车流量、机动车速度、非机动车速度等.各事件单元并非独立,事件链中前一个事件单元运行结束时的时刻和速度,是下一个事件单元的初始时刻和速度,因此机动车右转事件链是由时空上存在关联的事件单元构成.
事件单元的几何参数如图2所示.事件单元的几何区域包括两个部分,第一部分为右转车与冲突交通流的冲突交织区,如图中的la表示区域;第二部分为该交织区与下一事件单元之间的非冲突交织区,用lb表示,表示相邻两个事件单元之间的位置关系.由于交叉口的设计不同,各个事件单元的位置关系也不同.当lb>0,表示相邻的两个事件单元在空间上不重叠;当lb≤0,表示相邻的两个事件单元在空间上重叠,重叠部分的长度为lb.
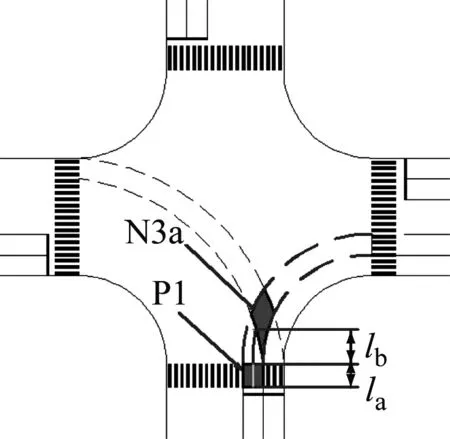
图2 事件单元几何尺寸示意图Fig.2 Geometric dimensions of events
2 右转事件链可靠度
2.1 可靠度定义
可靠性是用概率定义的,即在一定的时间内,在一定的条件下完成规定功能的能力[6].因此,将交叉口右转事件链可靠度定义为:在一个信号周期内,平均日交通量荷载作用下,右转机动车不发生严重冲突顺利通过交叉口的概率.
记Xi事件单元的安全可靠度为Ri,事件单元Xi的失效率为λi,则
λi=1-Ri
(1)

记Aj表示“Xj事件处于相位j中”,Bi表示“Xi事件失效”,λi实际上表示一个信号周期中相位j条件下Xi失效的概率,即λi是一个条件概率,即
λi=P(Bi|Aj)
(2)
则“相位j”与“Xi事件失效”同时发生的概率为
P(AjBi)=P(Aj)P(Bi|Aj)=wjλj
(3)
一个周期内右转事件链包含8种冲突事件,系统失效率用下式计算:
(4)
则右转事件链系统可靠度为
R*=1-λ*
(5)
2.2 事件单元失效模型
2.2.1数据准备
在上海市区选取7个交叉口采集冲突数据.交叉口满足以下条件:四相位,至少含有行人或非机动车其中一种,交叉口的右转设计未设置渠化岛.每个交叉口视频录像24 h.视频资料初步处理后,利用George 2.1软件拾取交叉口内的运动信息,获得运动物体的位置坐标、速度、加速度、轨迹等.结合交通冲突理论,计算右转机动车交通冲突参数.
2.2.2严重冲突临界值
对于严重冲突,大量研究采用先估算速度,进而判断车辆距离目标可能发生事故的冲突时间(tTTC, time to collision),判断是否发生严重冲突.当tTTC小于某一临界值为严重冲突,否则为非严重冲突.美国公路研究所提出的临界值是1 s,瑞典是1.5 s[7].国内学者选择85%累计频率对应冲突时间作为严重冲突与一般冲突分界点,得到临界值为1 s[8].因此,本文计算右转机动车与冲突对象的tTTC,当tTTC<1 s,则认为发生严重冲突,即事件单元失效.
2.2.3失效模型
交叉口内tTTC受多因素影响,例如速度、交通量、信号相位等.考虑事件单元发生过程量化参数较多,计算复杂,选择右转车进入事件单元的初始速度vin,冲突对象平均速度vn,事件单元内的冲突对象数量N作为自变量建立模型.在进行参数检验过程中发现,严重冲突率与vin、|vin-vn|均有较强相关性.对于冲突对象数量N,当N较小时,严重冲突的概率随着N的增大而增大;当N较大时,严重冲突的概率随着N的增大而减小,即存在一个临界值n.二元Logistic模型形式如下:
tTTC=1/(1+exp(-α+β1vin+β2|vin-vn|+
β3|N-n|))
(6)
结合视频提取的冲突数据,利用Spss软件进行模型拟合,统计结果如表1所示.
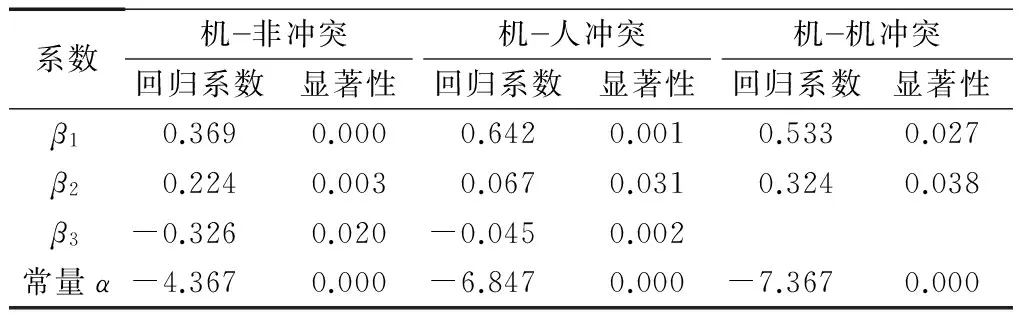
表1 Logistic模型拟合结果Tab.1 Logistic model fitting results
(1) N1、N2、N3a、N3b事件单元失效Logistic模型
tTTC=1/(1+exp(-4.367+0.396vin+
0.224|vin-vn|-0.326|N-1.5|))
(7)
模型预测的准确率为70.9%.
(2) P1、P2事件单元失效Logistic模型
tTTC=1/(1+exp(-6.847+0.642vin+
0.067|vin-vn|-0.045|N-1|))
(8)
模型预测的准确率为73.3%.
(3) M1、M3事件单元失效Logistic模型
对于直行机动车造成的冲突,由于某一时刻一条机动车道只有一辆直行车通过,因此N值始终保持0或1.
tTTC=1/(1+exp(-7.367+0.533vin+
0.324|vin-vn|))
(9)
模型预测的准确率为67.1%.
3 右转事件链延误
利用排队论的理论计算右转事件链的车均延误.对于交叉口右转机动车,认为系统是泊松输入、负指数分布、N个服务台的排队系统,用M/M/N表示,此时排队等待通过的通道只有单独一条.
设右转车辆平均到达率为λ,平均服务率为μ,记ρ=λ/μ.
右转事件链内没有右转车辆的概率为
(10)
右转事件链以及排队等候区有k辆右转车辆的概率为
(11)
(12)
右转事件链以及排队等候的平均右转车辆数为
(13)

(14)
右转车辆的平均消耗时间为
(15)
4 系统模拟计算
4.1 蒙特卡洛法
交通流具有随机分布特征,非常适合用蒙特卡洛法进行分析.蒙特卡洛法(Monte-Carlo)是利用随机抽样进行系统模拟的方法.Khoury等[9]采用蒙特卡洛法计算超车视距受到限制的概率.陈欢欢等[10]采用蒙特卡罗数值模拟计算交叉口可靠度,其结果表明,蒙特卡罗法计算过程简便合理.蒙塔卡洛法系统模拟之前,需要对交叉口进行观测,归纳其随机参量的先验分布形式和统计参数,构造概率分布相似的随机数.
由概率论和数理统计对概率的定义可知,某一件事情发生的概率,可以用该事件在大量重复的抽样试验中出现的频率来表示.自编MATLAB程序模拟运行参量,随机生成大量样本,将其输入右转事件链模型.蒙特卡洛系统模拟的周期样本量为N,某一事件单元周期失效数为K,事件单元Xi的安全可靠度为
PXi=1-K/Nwj
(16)
(17)
4.2 事件链发生过程
交叉口右转事件链模拟过程中,当右转车辆进入事件单元时,首先判断该事件单元是否会发生冲突.如果无冲突发生,则右转车辆服从无干扰状态下的行车规律经过该事件单元;如果有交通冲突,则服从冲突干扰状态下的行车规律.以N1事件单元为例,右转机动车在经过该事件单元的过程如下:
情况(1) N1单元内有交通冲突
Step 1 求右转车进入N1事件单元第二部分时的车速vmid与右转车在进入N1事件单元第二部分时的时刻tmid.
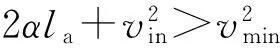

式中:α为第i辆右转车在进入N1事件单元时,受到冲突影响下的加速度,根据视频数据采用;la为N1冲突交织区的长度;vin为右转车进入N1事件单元时的车速;vmin为右转车在受到干扰状态下能够保持的最低车速;tin为右转车在进入N1事件单元时的时刻.
Step 2 求右转车驶离N1事件单元时的车速vout与右转车在驶离N1事件单元时的时刻tout.

当之前的车速出现过大于vmin的情况时
其他情况
式中:vmin为右转车在无干扰转弯过程中预期的最低车速;lb为N1非冲突交织区的长度;α1为右转车在无冲突干扰状态下减速时的加速度;α2为右转车在无冲突干扰状态下加速时的加速度.
Step 3vout成为进入下一个事件单元的vin,tout成为进入下一个事件单元的tin.
情况(2) N1事件单元内无交通冲突发生
Step 1 求vout与tout
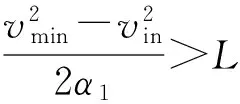
当之前的车速出现过大于vmin的情况时
其他情况
式中:L为N1事件单元的长度,L=la+lb.
Step 2vout成为进入下一个事件单元的vin,tout成为进入下一个事件单元的tin.
5 案例分析
上海市某大型交叉口形状规则,四相位控制,交叉口长50 m,转弯半径15 m,如图3所示.信号配时方案为:phase 1为70 s,phase 2为60 s,phase 3为30 s,phase 4为40 s.进口道设有右转专用车道,右转车流量较大,510辆·h-1.对交叉口内流量进行调查,结果如表3所示.根据交叉口的几何设计条件,计算得到事件链尺寸如表3所示.通过现场调查法,获得右转车辆进入事件链的速度平均值和标准差分别为19.74、19.89 km·h-1,车速离散性较大.该交叉口内大部分交通参与者遵循信号控制通行.

图3 交叉口示意图Fig.3 Schematic diagram of the intersection表3 交叉口流量与事件链尺寸表Tab.3 Intersection flow and dimension of event chain

事件单元流量/(辆·h-1)事件单元尺寸/mP1700la=4.00,lb=5.79,S=3.50N3a160la=3.60,lb=-2.13,S=11.66N2480la=6.25,lb=1.15,S=13.69N1500la=6.29,lb=-1.60,S=40.40N3b30la=5.67,lb=-4.06,S=44.53M1320la=9.24,lb=-5.18,S=45.78M360la=5.18,lb=0,S=43.91P2900la=4.00,lb=0,S=3.50
注:S为冲突对象停车线(等待)位置与事件单元冲突区域中心位置之间的距离.
5.1 评估准则
相关心理研究表明[11],胆大的人能接受的危险率不超过10-3,谨慎的人能接受的危险率不超过10-4.道路交通中处处隐含着危险,驾驶人的行为即体现足够的胆量又包含着谨慎.交叉口是城市道路交通中矛盾的集中地,综合考虑,采用10-3作为右转事件链可接受的失效概率,即设定目标可靠度为0.999,延误评价准则见表4[4].
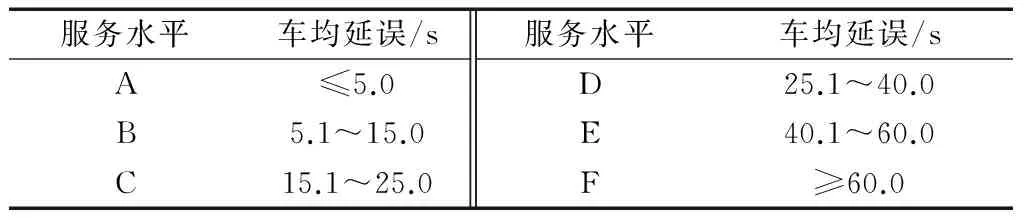
表4 信号交叉口延误与服务水平Tab.4 Signalized intersection delays and service levels
5.2 评估结果与改善
根据前面建立的事件链模型,在MATLAB平台上编制交叉口右转模拟程序.将交叉口的调查参数输入,利用蒙特卡洛模拟实验进行10 000次抽样计算,结果见表5.车均延误d为14.849 s.回看交叉口录像视频,利用点样本法算出平均延误d点为13.670 s.两种计算方法误差为|d-d点|/d点=|14.849-13.670|/13.670≈8.62%.由于点样本法未考虑车辆起制动加减速所需的时间,计算结果一般小于实际延误.点样本法计算结果小于蒙特卡洛模拟结果,同时二者误差小于10%,说明模拟结果有效.
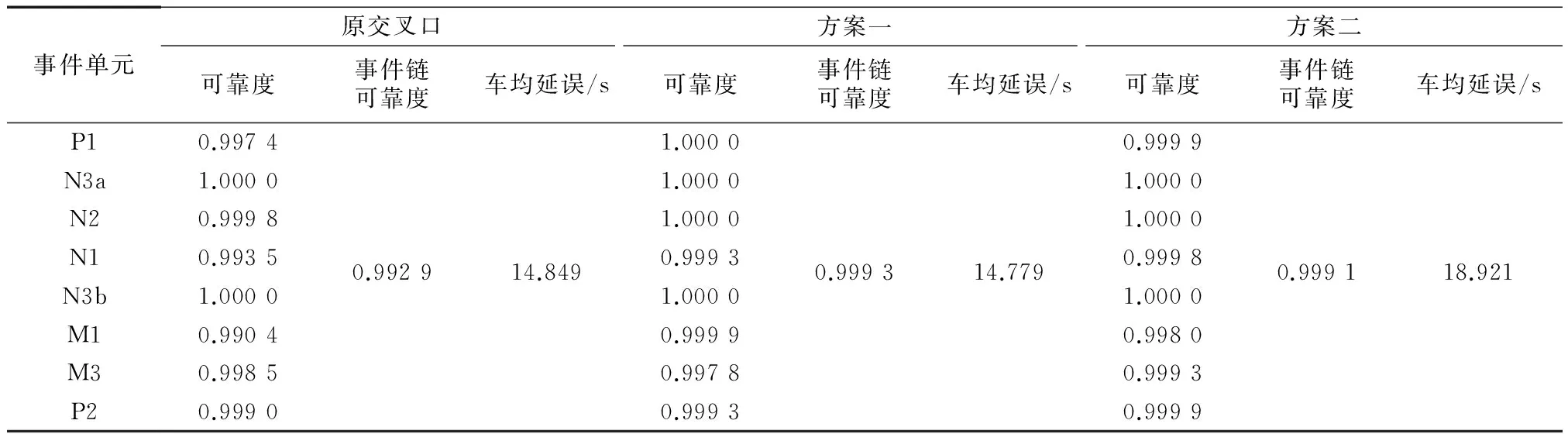
表5 交叉口可靠度与延误计算结果Tab.5 Calculation results of reliability and delay of intersection
该交叉口右转车可靠度为0.992 9,安全状况不满足要求;就延误而言,处于B级服务水平,车流稳定,稍有延误.事件单元M1的可靠度最低,是导致系统可靠度低的主要原因.
为了提高系统可靠度,改善方案的思路之一为避免可靠度最差的事件单元发生.M1在phase 1阶段发生,考虑缩短phase 1时间.调整后的配时方案为方案一:phase 1为50 s,phase 2为50 s,phase 3为40 s,phase 4为60 s.事件链可靠度为0.999 3,达到了可接受的安全性要求;车均延误缩短了0.07 s,依然处于B级服务水平.
由事件链的属性可知,事件单元几何尺寸影响可靠度与延误.改善方案的思路之二为减少事件单元的尺寸,让右转冲突区域更加集中.在原方案基础上,将人行道向交叉口中心平移10 m,形成方案二.右转事件链可靠度达到0.999 1,满足了安全性要求;但是车均延误比原交叉口增长了3.63 s,处于C级服务水平.方案二牺牲了较多效率.
除了以上两种改善方案外,还存在许多其他改善方案.深入分析事件链及系统模拟结果,有助于快速定位导致安全性低或效率低的因素,制定出有效的改善措施.
6 结语
本研究提出了城市道路交叉口右转安全性和效率的综合性评估方法.建立右转事件链模型,分析右转过程8种冲突事件,详细解析了右转事件链的属性及发生过程,使得平面交叉口机动车右转过程变得更为清晰.右转事件链将交叉口复杂变量(几何设计条件、交通量特征、交通控制方案等)与冲突和延误建立了联系,使导致安全或延误的不利因素能得到解释,有助于提出针对性的改善方案.采用蒙特卡洛系统模拟计算交叉口评估指标,既可以对交叉口进行后评估,也可以用于方案设计阶段的交叉口评估,即前评估,提前发现交叉口存在的问题.研究仍然存在需要改进的地方,由于引发严重冲突的原因较为复杂,后续的研究将进一步提高事件单元失效模型精度.
参考文献:
[1] TARRALL M, DIXON K. Conflict analysis for double left-turn lanes with protected-plus-permitted signal phases[J]. Transportation Research Record: Journal of the Transportation Research Board, 1998, 1635(1): 105.
[2] SAYED T, ZEIN S. Traffic conflict standards for intersections[J]. Transportation Planning & Technology, 2007, 22(4): 309.
[3] 潘福全,陆键,项乔君,等.公路信号平面交叉口安全服务水平研究[J].东南大学学报(自然科学版),2008,38(2):298.
PAN Fuquan, LU Jian, XIANG Qiaojun,etal. Level of safety for highway signalized intersections[J]. Journal of Southeast University (Natural Science),2008,38(2):298.
[4] 张鹏,赵静,王占宇,等. 蒙特卡罗法在评价交叉口服务水平中的应用[J]. 黑龙江工程学院学报(自然科学版), 2009, 23(1): 44.
ZHANG Peng, ZHAO Jing, WANG Zhanyu,etal. Application of Monte Carlo in assessment of the service level of signal intersection[J]. Journal of Heilongjiang Institute of Technology (Natural Science), 2009, 23(1): 44.
[5] 张学亮,邓卫,郭唐仪. 基于冲突率的交叉口交通安全评价方法研究[J]. 交通运输工程与信息学报, 2007, 5(1): 85.
ZHANG Xueliang, DENG Wei, GUO Tangyi. Development of traffic safety evaluation method based on TCT at grade crossings[J]. Journal of Transportation Engineering and Information, 2007, 5(1):85.
[6] CHOI S K, CANFIELD R A, GRANDHI R V. Reliability-based structural design[M]. London: Springer, 2007.
[7] LAURESHYN A, SVENSSON Å, HYDEN C. Evaluation of traffic safety, based on micro-level behavioural data: theoretical framework and first implementation[J]. Accident Analysis and Prevention, 2010, 42(6): 1637.
[8] 刘淼淼,鲁光泉,王云鹏,等. 交叉口交通冲突严重程度量化方法[J]. 交通运输工程学报, 2012, 12(3): 120.
LIU Miaomiao, LU Guangquan, WANG Yunpeng,etal. Quantitative method of traffic conflict severity at intersection[J]. Journal of Traffic and Transportation Engineering, 2012, 12(3): 120.
[9] KHOURY J E, HOBEIKA A G. Assessing the risk in the design of passing sight distances[J]. Journal of Transportation Engineering, 2007, 133(6): 370.
[10] 陈欢欢,王福建,项贻强,等. 基于蒙特卡罗数值模拟的信号交叉口可靠性研究[J]. 交通标准化, 2007(1): 60.
CHEN Huanhuan, WANG Fujian, XIANG Yiqiang,etal. Research on reliability of signalized inter-sections based on Monte-Carlo numerical simulation[J]. Communications Standardization, 2007(1): 60.
[11] 陈富坚,郭忠印,陈富强,等. 公路平曲线半径的可靠性设计[J]. 哈尔滨工业大学学报, 2012, 44(4): 100.
CHEN Fujian, GUO Zhongyin, CHEN Fuqian,etal. Reliability design method for horizontal curve radius of highway alignment[J]. Journal of Harbin Institute of Technology, 2012, 44(4):100.

