基于多层中轴点拟合的古塔变形检测

刘世杰， 郭成成， 王穗辉， 童小华

(1.同济大学 测绘与地理信息学院，上海 200092;2.同济大学 土木工程防灾国家重点实验室， 上海 200092)

古塔是具有历史价值、艺术价值和人文价值的国家文物，是国家不可再生的文化资源.现存的古塔对研究我国古代建筑史、宗教史和地方史具有重要的意义.但由于历史、地质、战争等原因，使得古塔倾斜、损坏的现象十分普遍，所谓“十塔九歪”.因此只有对古塔质量建立科学的评价体系，进行及时的保护和修缮，才能延长古塔寿命，继续发挥其独特的价值[1].

在古塔保护、维修的过程中，首先应该对古塔的倾斜变形进行评估.传统的古塔倾斜测量方法首先在古塔周围建立局部平面坐标系，在塔底进行测量得到塔底多边形，采用多边形拟合或对角线相交的方法确定底部几何中心，再将测量得到的塔顶三维坐标投影到底部，计算出投影点与底部中心的距离，根据此距离与塔高的比值计算倾斜程度[2].传统方法仅用塔底几何中心和塔顶的连线来表征古塔姿态，并未反映出古塔的分层变形情况.刘琦等[3]提出将古塔每层的8个观测点投影到水平面上，然后应用最小二乘技术进行圆拟合获取每层中心，但在实际的测量中，塔身及塔体棱角多会受到破坏而模糊，难以对棱角点进行准确观测.周千[4]提出把到各层观测点距离平方和最小的点作为各层中心点，进而对中心点拟合空间轴线，其方法对观测点的质量有较高要求且难以确定实际塔体测量点.Tang等[5]通过测量点拟合表征古塔的正交横截面，将横截面交线作为塔体空间轴线，进而计算整体倾斜程度.

本文提出了一种新的古塔变形观测与计算方法，对古塔的姿态进行全面客观的描述.使用全站仪对古塔墙面进行点位观测，获取墙面观测点位的三维坐标数据，通过多层中轴点拟合计算古塔倾斜和扭曲变形.基于本文提出的方法，以安徽省安庆市的振风塔为例，进行了数据采集和变形分析，验证了方法的有效性.

1 实验对象和测量数据

实验对象为安徽省安庆市的振风塔，坐落在长江之畔，建于公元1570年，至今已有400多年历史，享有“万里长江第一塔”、“过了安庆不说塔”的美誉，是七层八角楼阁式建筑，如图1所示.

图1 振风塔Fig.1 Zhenfeng Pagoda

首先在振风塔四周建立了包含15条测边的闭合导线网进行控制测量，建立独立坐标系，选取某一地面控制点为原点，以南北方向的两个控制点所在直线向北为x轴方向，与这两点所在直线垂线往东向为y轴方向.然后在布设的导线控制网中，将全站仪架设在观测条件良好的控制点上对古塔各层的每一墙面观测均匀分布的5～6个点位以进行平面拟合，并测量了塔尖三维坐标，墙面平整度较差时需增加观测点数量以减小表面方程表征墙面的误差.部分观测数据如表1所示.为了便于点位观测数据管理，对观测点位进行了编号，其中观测点编号的首位表示对应的古塔墙面序号，中间位表示塔层，末位表示相应塔层墙面的观测点号.如表1中872号观测点，表示古塔第7层第8面的2号观测点.

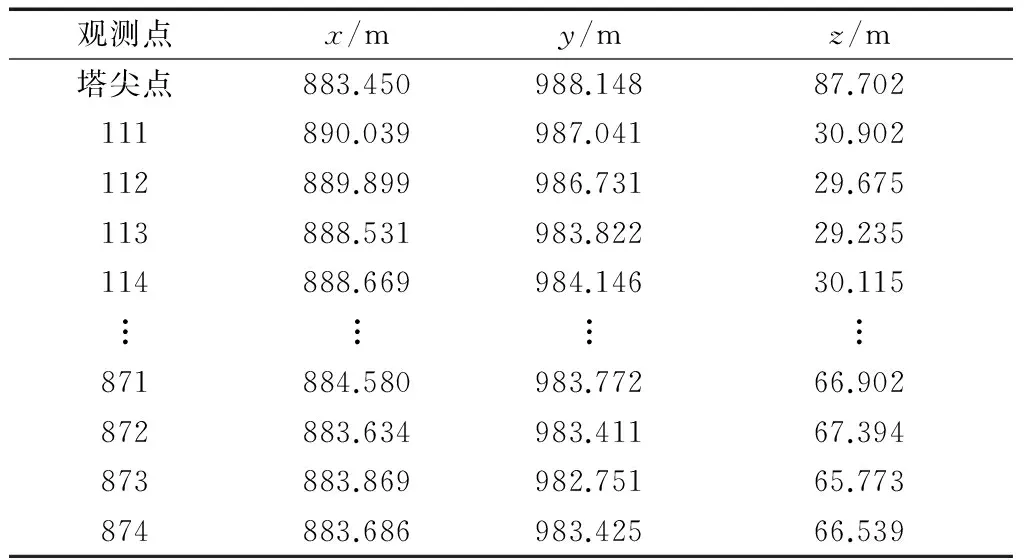
表1 全站仪部分观测数据Tab.1 Part of the observed data of total station

振风塔各层墙面测量点位分布如图2所示.

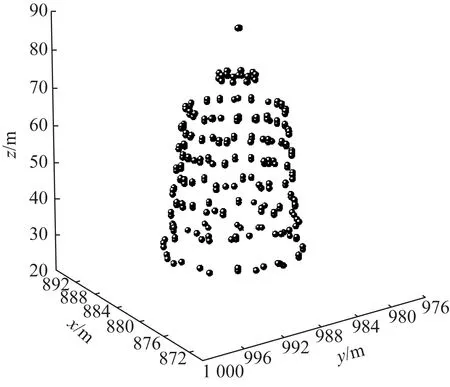
图2 振风塔墙面观测点分布Fig.2 Distribution of measurement pointson Zhenfeng Pagoda

2 多层中轴点拟合变形检测方法

本文提出的基于多层中轴点拟合的古塔变形检测流程如图3所示，包括平面拟合与棱线确定、各层棱角点和中轴点坐标计算、变形参数计算等步骤.

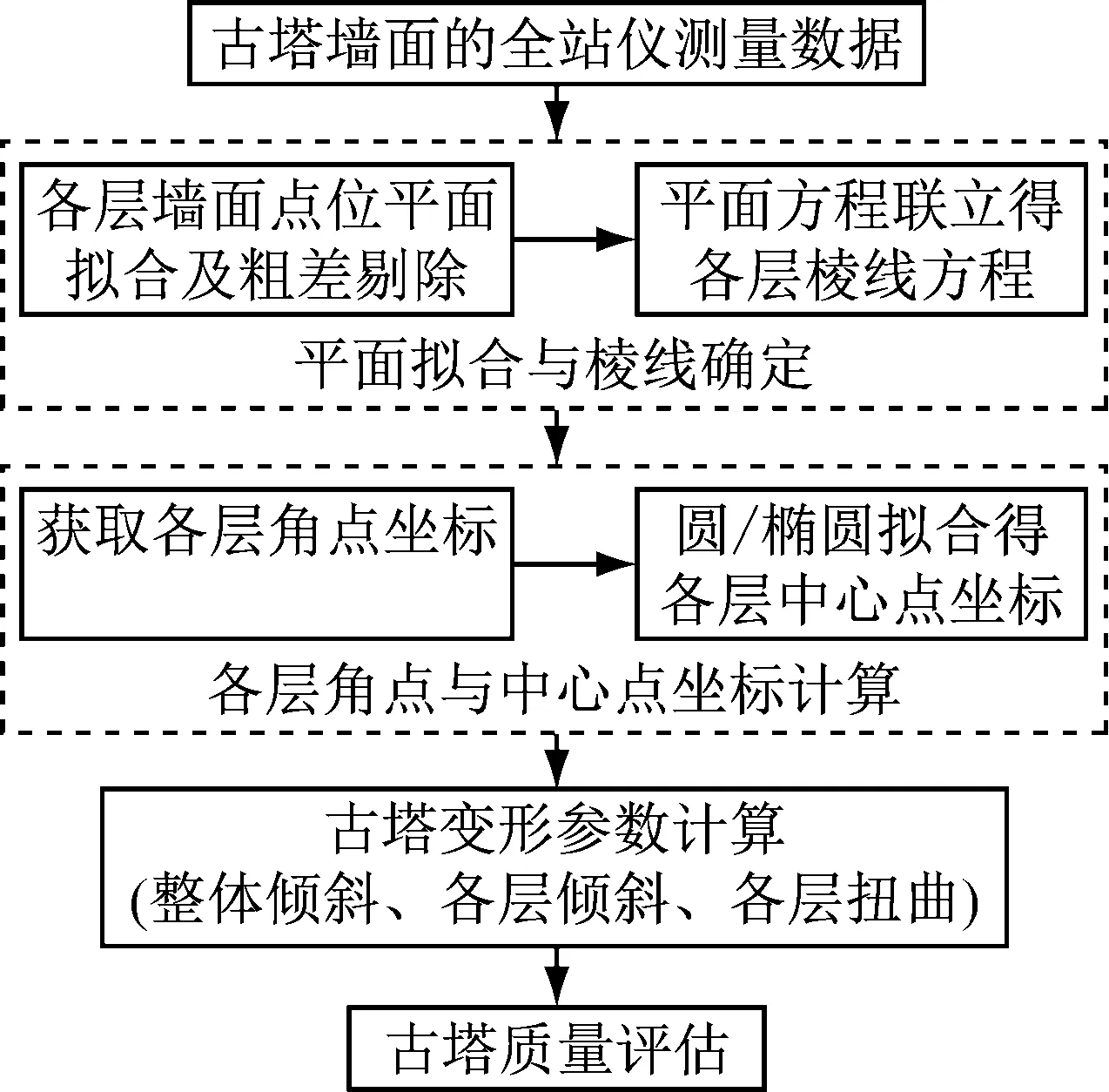
图3 基于多层中轴点拟合的古塔变形检测流程图Fig.3 Flowchart of pagoda deformation estimationbased on multilayer central points’ fitting

2.1 平面拟合与棱线确定

整体最小二乘平差(TLS)方法在参数求解中同时考虑系数矩阵和观测向量存在的误差.TLS是以系数矩阵和观测向量的残差改正数的F范数极小为约束准则，求解未知参数.考虑到系数矩阵包含随机误差，整体最小二乘平差方法在拟合精度上要优于普通最小二乘法[6-8].其估计准则如下：

(1)

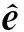
对全站仪测量数据进行处理.分别对每一层每一面的平面方程进行拟合，由于系数矩阵由观测值构成，存在测量误差，故在求解平面方程系数的最优估值时采用整体最小二乘平差方法.得到各面的平面方程后，将相邻墙面平面方程联立得到对应塔层的棱线方程，如式2所示.

(2)

式中：(a1,b1,c1)、(a2,b2,c2)分别为两平面的法向量.则相应的棱线方程为

(3)

通过棱线方程确定的不同高度处的棱角点坐标决定着后续倾斜计算的精度.这里对x关于z的棱线方程进行微分，分析平面系数误差与棱角点坐标误差的关系.

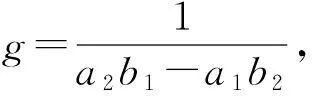
x=(b1-b2)g+(c1b2-b1c2)zg

计算x关于平面方程系数的导数，结果如下：

(4)

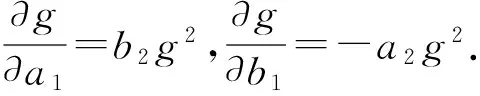
(5)

同理可得x、y关于a2、b2、c2的导数，则有如下关系式：

(6)

将古塔墙面拟合系数代入式(6)计算导数值，可发现在高程值确定的条件下，棱角点坐标对平面拟合系数的变化较为敏感，因此须保证墙面观测点的精度.通过平面拟合残差检测粗差点(偏离拟合平面三倍中误差)并剔除，以提高古塔墙面拟合的精度，从而保证棱线和棱角点精度.

2.2 各层棱角点和中轴点坐标计算

得到各层相邻墙面棱线方程后，给定高程值即可得到对应高程面的棱角点坐标.实验中选取了各层所有观测点的高程均值作为相应塔层棱角点计算的高程值，然后对每层的8个棱角点坐标进行圆或椭圆拟合，计算各层中轴点.

圆曲线方程如下：

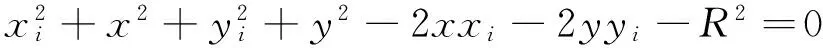
(7)

式中：(xi,yi)为棱角点坐标；(x,y)为待求中心点坐标；R为半径.

古塔发生倾斜变形后，同一高程上的各个棱角点会因变形而构成一个椭圆，椭圆曲线方程如下：

Ax2+Bxy+Cy2+Dx+Ey+1=0

(8)

式中：A、B、C、D、E为系数.

椭圆中心坐标为

(9)

圆或椭圆平差拟合过程中系数矩阵包含了坐标测量误差项和常数项，故采用混合最小二乘法进行参数求解，其求解原则是系数矩阵的误差项和整体残差的F范数最小,如下式所示：

(10)

式中：A2为设计矩阵误差项；y为观测量.

2.3 古塔变形参数计算

得到古塔各层中轴点坐标后，对表征古塔整体倾斜度的中心轴线进行整体最小二乘拟合[9-10]，并计算古塔变形参数来评估古塔变形状态.古塔变形参数包括古塔倾斜度、偏移量、各层倾斜度以及扭曲度等.倾斜度用古塔各层中心拟合轴线与竖直方向的夹角来表示.偏移量定义为塔尖偏离塔底中心的距离，可以分解为东西和南北两个方向偏移分量.为了细致描述古塔变形，可以计算古塔的各层倾斜度，即每一层的几何中心与底部中心连线向量与竖直向量的夹角.古塔的各层为多边形结构，通过计算各层棱角点构成的多边形之间的旋转角度得到古塔相邻层之间的扭曲度，进而对其扭曲状态进行详细评估.

3 结果与分析

基于古塔各层墙面观测点拟合空间平面，在平面拟合计算过程中，检测到第7层第8面中存在一个粗差观测值，导致该平面拟合误差较大，最大距离达200 mm，经剔除后，平面拟合误差在5 mm以内.所有有效观测点到相应拟合平面的距离分布，如图4所示.由图4可以看出，大部分点到平面的距离在1 mm以内，3 mm以内的观测点占90%，所有有效观测点到相应拟合平面的最大距离不超过6 mm.

图4 墙面观测点到拟合平面距离分布图Fig.4 Distribution of distance betweenobservation points and fitting plane

在求解各层相邻墙面棱线方程的基础上，将高程值带入解算棱角点坐标，进而计算得到古塔各层中轴点坐标，如表2所示.表2列出了基于圆拟合和椭圆拟合的结果及均方根误差，可以看出，两种拟合方法得到的各层中心坐标几乎一致.均方根误差显示椭圆拟合精度高于圆拟合精度，这也符合古塔在发生倾斜时，等高程的各角点的分布更接近椭圆曲线.

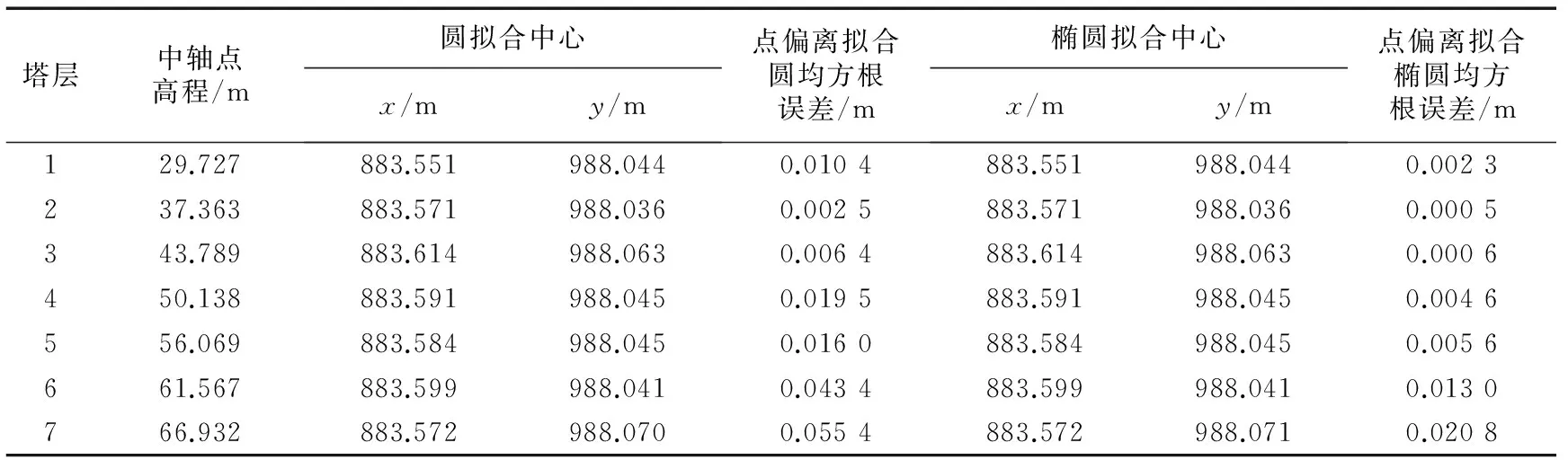
表2 各层中心坐标及拟合误差Tab.2 Center coordinates of each layer and standard deviation of fitting

利用中轴点及塔尖点坐标进行整体最小二乘拟合得到古塔中心轴线为

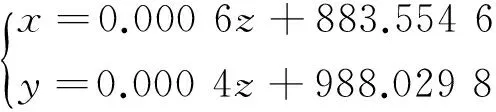
各层中轴点、塔尖点及拟合空间轴线如图5所示.

拟合中心空间轴线向量为(0.000 6，0.000 4,1.000 0)，计算其倾斜角为2′28.74″，倾斜率约为1/1 400，此为振风塔的整体倾斜度.由于轴线拟合的平差特性，可能会使得计算出的倾斜度偏小.利用传统的塔顶、塔底中心的水平投影偏移与塔高的比值来计算整体倾斜度，其结果为7′30.2″，倾斜率约为1/460.通过第1层中轴点和塔尖坐标计算古塔偏移量，南北方向为0.037 m，东西方向为0.121 m，整体向东北方向倾斜.由于塔尖单点测量的不准确性和塔尖结构的晃动，塔尖所反映的变形往往误差较大.古塔各层倾斜度及扭曲度计算结果如表3所示.

变形计算结果显示，古塔倾斜量很小，说明基础及塔体依然稳固.古塔各层倾斜程度并不完全一致，其中第1层到第3层的倾斜度相对较大，达16′，倾斜率约为1/210.其原因有待后续进一步观测确定.如果后续观测呈现一样的倾斜特征，则可能该倾斜特征在该塔建造之时即存在，即在建造完第3层发现相对倾斜后对上层予以纠正，从而呈现计算得出的倾斜分布.此外，扭曲度结果显示，相邻塔层多边形结构的扭曲程度不大，均在8′以内.目前对古塔倾斜的允许值还未建立相应的标准，应定期对古塔进行倾斜测量，在古塔周围环境发生较大变化时应当增加观测频率，通过古塔观测的序列数据来分析变形趋势及制订相应的保护措施.

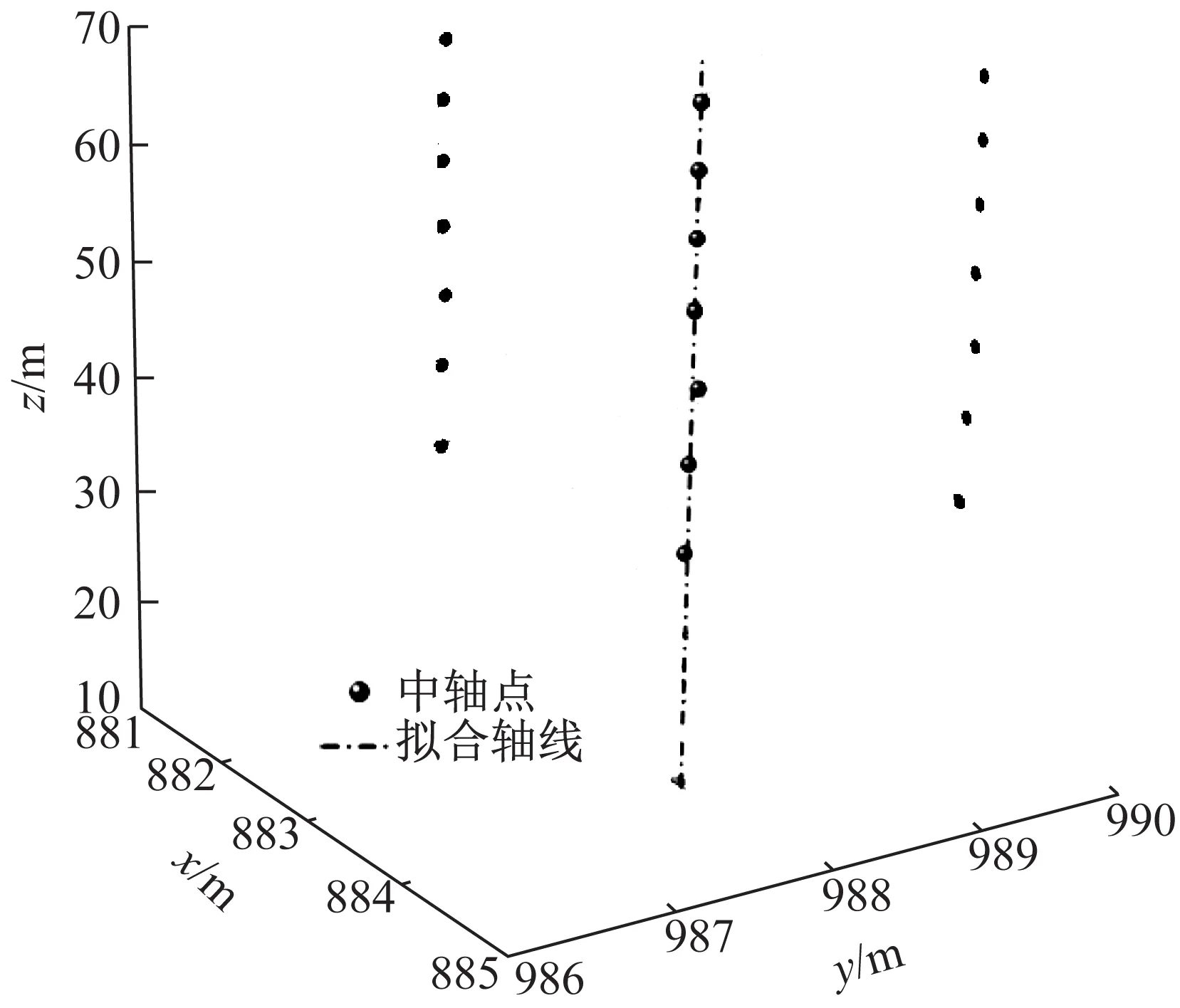
图5 多层中轴点分布及空间轴线拟合示意图Fig.5 Distribution of multilayer centralpoints and spatial axis fitting表3 古塔各层倾斜度及扭曲度Tab.3 Inclination and twist of each layer of pagoda

塔层倾斜度相邻塔层扭曲度129'40.76″121'5.36″1316'5.16″237'59.68″146'44.22″347'28.77″154'18.4″455'41.06″165'11.6″567'23.70″173'5.17″675'1.34″

4 结语

为了精确检测古塔变形，本文利用全站仪对古塔的每一层每一面进行点位测量，保证每一面都有足够数量均匀分布的测量点以拟合平面方程，然后拟合计算各层中轴点坐标，进而计算古塔的倾斜量、偏移量、各层倾斜度和扭曲度等变形参数，并通过振风塔变形检测实验验证了本文方法的有效性.相比传统方法仅用塔底几何中心和塔顶的连线来表征古塔倾斜变形，通过多层中轴点计算及古塔空间轴线拟合，获取了更加详尽的古塔变形数据及规律，为其进一步的修缮和维护提供了更详细的依据.因此，本文方法对于古塔等建筑物变形检测工程实践具有一定的指导和参考借鉴作用.

参考文献:

[1] 梁海奎.古塔变形测量方法探讨[J].城市勘测，2011(3)：113.

LIANG Haikui. The discussion of monitoring ancient buddhist pagoda deformation [J].Urban Geotechnical Investigation & Surveying, 2011(3): 113.

[2] 黄强.古塔变形监测探讨[J]. 测绘与空间地理信息，2013(6)：218.

HUANG Qiang. Discussion on deformation monitoring of old towers [J].Geomatics & Spatial Information Technology, 2013(6):218.

[3] 刘琦, 惠小健, 李永新. 古塔变形问题研究[J]. 黑河学院学报, 2015, 6(3):120.

LIU Qi, HUI Xiaojian, LI Yongxin. Study on the deformation of pagoda [J]. Journal of Heihe University, 2015, 6(3):120.

[4] 周千. 基于数学模型的古塔变形问题研究[J]. 计算机与数字工程, 2014, 42(8):1346.

ZHOU Qian. Study on pagoda deformation based on mathematical model [J]. Computer and Digital Engineering, 2014, 42(8):1346.

[5] TANG Yongjing, SHAO Zhendong, KUJAWSKI E. Zhenfeng tower maintenance and its durability[C]∥Proceedings of Third International Workshop on Civil Structural Health Monitoring. Vancouver: The University of British Columbia, 2010: 421-428.

[6] 王穗辉.误差理论与测量平差[M].上海:同济大学出版社,2010.

WANG Suihui, Error theory and surveying adjusting[M]. Shanghai: Tongji University Press, 2010.

[7] 王安怡,陶本藻. 顾及自变量误差的回归分析理论和方法[J].勘测科学,2005(3)：29.

WANG Anyi, TAO Benzao. Theory and method of regression analysis for error of independent variable [J]. Site Investigation Science And Technology, 2005(3)：29.

[8] 鲁铁定,陶本藻,周世健.基于整体最小二乘法的线性回归建模和解[J].武汉大学学报:信息科学版,2008,33(5):504.

LU Tieding, TAO Benzao, ZHOU Shijian. Modeling and algorithm of linear regression based on total least squares [J]. Geomatics and Information Science of Wuhan University, 2008, 33(5):504.

[9] XU P L, LIU J N, SHI C. Total least squares adjustment in partial errors-in-variables model: algorithm and statistical analysis [J].Journal of Geodesy, 2012, 86(8):661.

[10] RYAN A G, MONTGOMERY D C, PECK E A,etal. Introduction to linear regression analysis, solutions manual to accompany [M].5th ed. Hoboken: Wiley, 2013.