承压板位置对混合塔结合部承载性能影响
王习之, 张光辉, 刘玉擎, 李永轩
(同济大学 土木工程学院, 上海 200092)
混合塔通过结合部将钢塔与混凝土塔竖桥向连接,形成混合结构.该桥塔构造形式于1945年首次应用于捷克共和国易北河上的玛丽安斜拉桥,其倾斜的混合塔结构具有良好的抗弯刚度和较轻的重量[1].1994年混合桥塔在日本的鹤见航道斜拉桥中也得了应用,其桥塔上部采用钢结构以获得纤细感,下部采用混凝土以应对不利的海洋条件[2].2000年以后,我国开始兴建混合塔斜拉桥,其中2005年建成的南京长江三桥是世界上跨径最大的混合塔斜拉桥.
混合塔的两种材料在竖向进行结合,明显增强了桥塔在高度方向上应对不同结构、美学以及环境要求的能力,使得桥塔在设计上更具有灵活性.然而桥塔结合部是两种材料的连接点,也是结构刚度的突变点,容易成为结构体系的薄弱部位[3-4].
混合塔结合部构造复杂,通常需结合模型试验对其进行研究.以往研究多集中于对单个工程实例的受力验证[5-7],或者是针对结合部中连接件的传力分析[8-11],针对结合部传力机理的研究、不同结合部类型之间的比较分析还比较少.本文以两座混合塔斜拉桥为工程背景,进行了前承压板式和后承压板式结合部模型承载性能模型试验,对两种结合部的受力特性、传力机理及差异进行了深入研究.
1 承压板式混合塔结合部构造特点
采用混合塔结构的斜拉桥如表1所示.结合部的构造形式按承压板的位置分为图1所示的前承压板式和后承压板式.
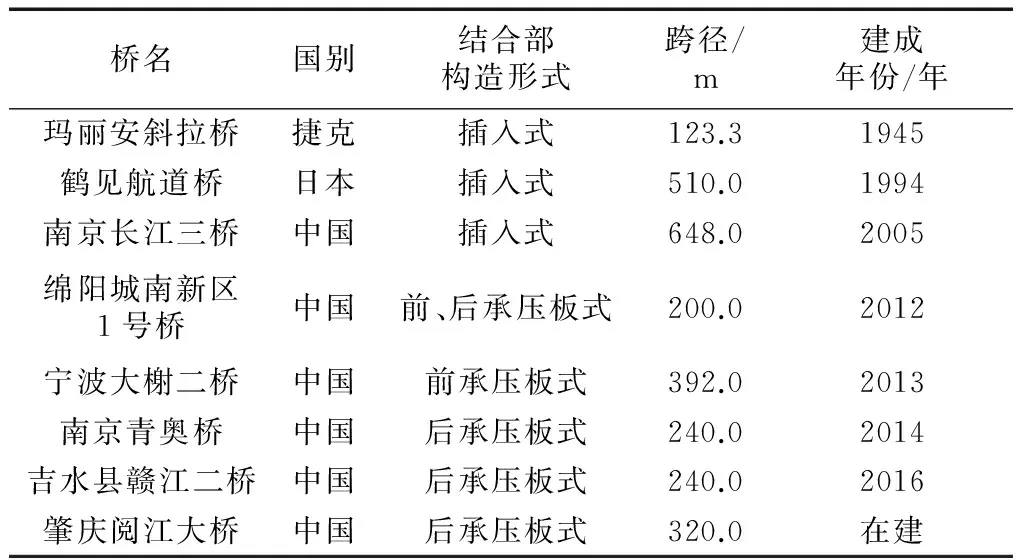
表1 混合塔斜拉桥工程实例Tab.1 Project of hybrid tower cable-stayed bridge
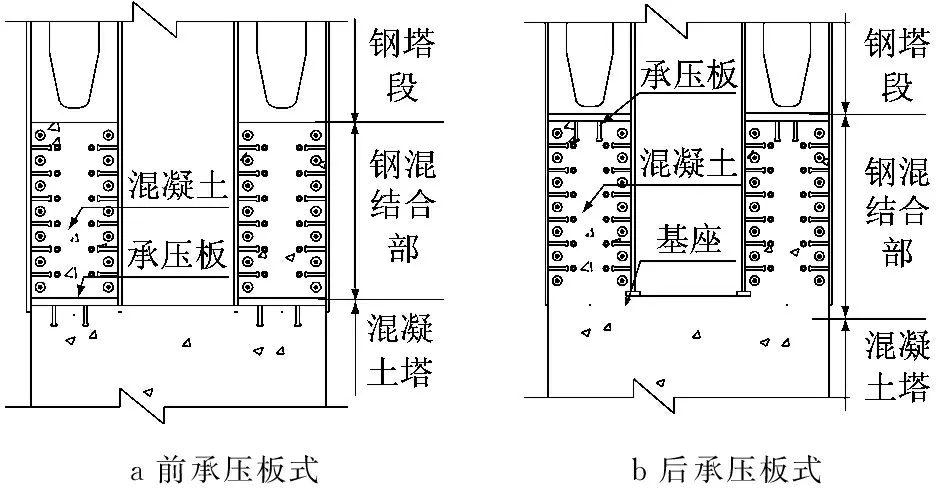
a前承压板式b后承压板式
图1结合部构造形式
Fig.1Structureofjointpart
前承压板式结合部承压板设置在靠近混凝土塔柱一侧.承压板一方面能使钢塔柱的应力进一步扩散,避免端部钢板对混凝土挤压,另一方面能有效减少钢和混凝土的相对滑移.在结合部中,利用钢结构的竖向加劲和两块纵桥向腹板,在结合部内形成格室,并在格室的壁板上布置焊钉或开孔板连接件.钢塔柱的轴力首先通过连接件将一部分轴力传递到混凝土塔柱,另一部分轴力通过底部设置的承压板传递到混凝土塔柱.宁波大榭二桥采用这种结合部构造形式.
后承压板式结合部承压板设置在靠近钢塔柱一侧,钢塔柱轴力首先通过承压板以接触承压的方式将一部分钢结构应力传递给混凝土塔柱,另一部分轴力通过连接件传递到混凝土塔柱中.后承压式结合部承压板传递的轴力较前承压板式大,承压板厚度较前承压板式大.南京青奥桥、吉水县赣江二桥等均采用这种构造.
2 前承压板式模型试验
2.1 前承压板式结合部构造
某桥塔钢-混凝土结合部构造如图2所示,结合部共10个格室,格室内填混凝土的高度均为3.05 m,每个格室钢板上焊钉所采用的规格、布置形式也大致相同,因此单个格室的受力状态能够较为真实地反应整个结合部受力.
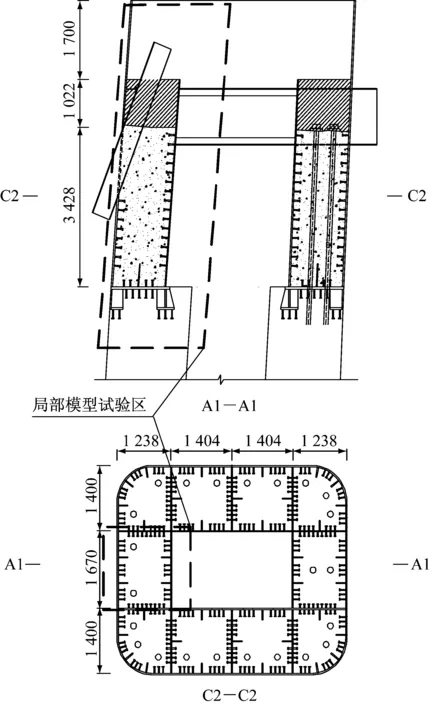
图2 前承压板式混合塔结合部构造(单位:mm)
Fig.2Structureofconnectionwithfrontbearingplate(unit:mm)
选取受力较大的格室及其下部混凝土结构进行局部模型试验,采用1∶2缩尺比设计结合部试验模型,钢板采用与实桥相同的Q345qD结构钢和相同等级的C50混凝土.承压板厚25 mm.为保证局部模型截面受力均匀,在预应力施加总力不变的情况下,共设置了4根预应力筋.按照抗剪刚度等效,焊钉连接件尺寸为Φ13 mm×90 mm,连接件竖向间距为110 mm.
根据等效应力换算,最不利工况下局部模型试验荷载P为2 260 kN,总预应力为1 840 kN,采用油压千斤顶对4根精轧螺纹钢筋施加预应力,每根精轧螺纹钢的张拉控制力为460 kN,预应力按50%、100%分级张拉.预应力施加后,轴力分别加载到1.0P和1.7P后卸载,加载等级为0.1P.加载之前先进行0.3P预加载,模型加载装置如图3所示.
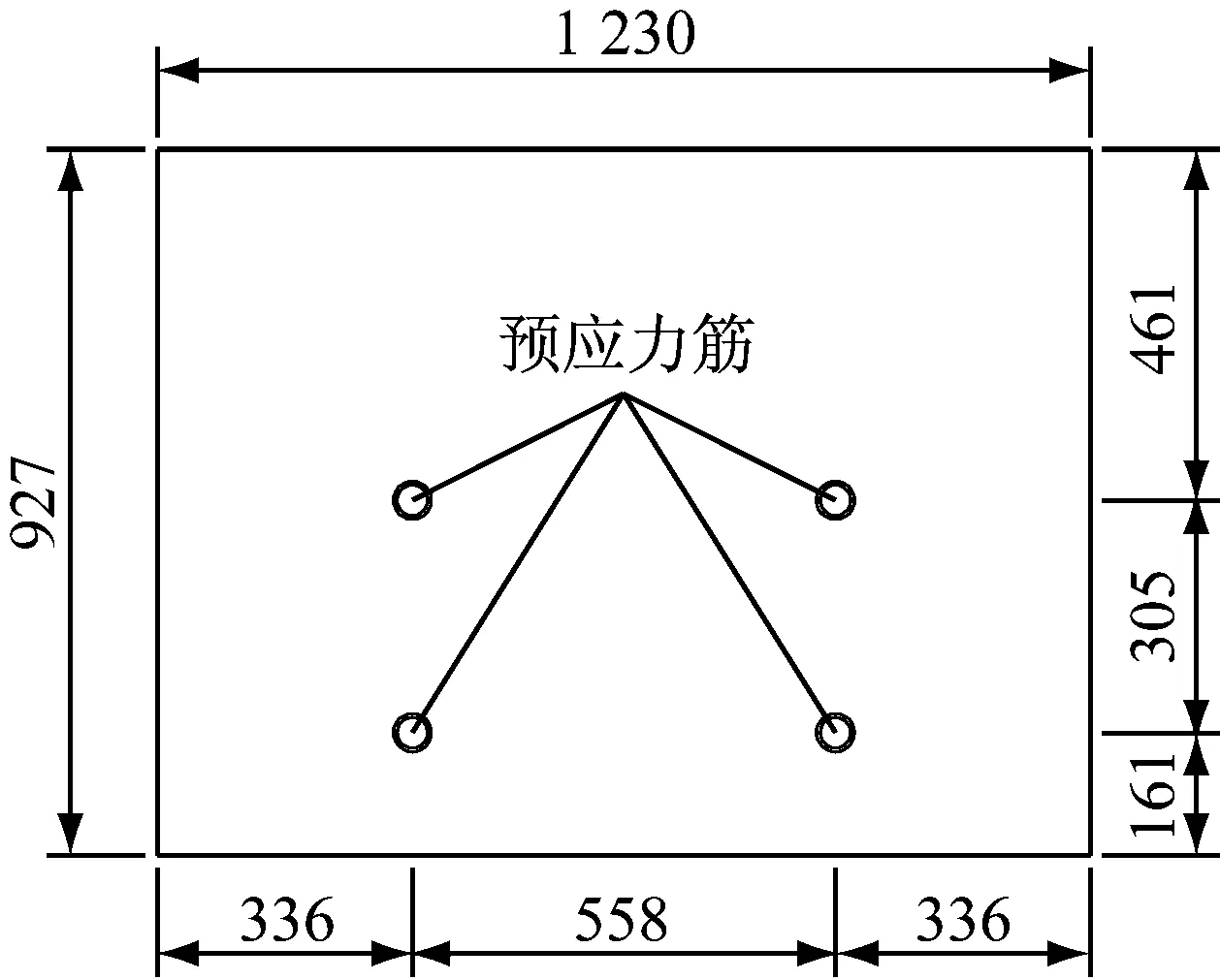
a 预应力加载位置

b 模型加载图3 局部模型加载装置(单位:mm)Fig.3 Load devices of partial model(unit: mm)
如图4所示,结合部钢结构主要受力钢板上布置了3列应变片,靠近承压板布置了较密的应变片.结合部内部从上往下设置了2列5排正弦计用以测试混凝土结构应变分布.混凝土顶部设置3个位移计用来测试钢与混凝土结构间的相对滑移.
2.2 前承压板式结合部钢板应力
图5为1.0P和1.7P荷载作用下,结合部各钢板竖向应力平均值的分布.钢板竖向应力从上往下呈逐渐减小的趋势,在距承压板0.8 m以上部位,钢结构竖向应力减少的趋势明显要快于0.8 m以下部位.随着荷载的增加,钢结构竖向应力减少的速率也有逐渐增加的趋势,说明随着荷载的增加,结合部钢结构和混凝土结构的相对滑移增加,焊钉传递作用的效率更加明显.钢结构竖向应力最大值出现在结合部混凝土顶面附近,最小值出现在承压板附近.
2.3 前承压板式结合部混凝土应力
图6为最不利荷载作用下,结合部混凝土竖向应力分布.混凝土应力在距承压板0.8 m以上部分逐渐增加,0.8 m以下部分混凝土应力增加的趋势变小或保持不变.结合部混凝土最大应力出现在承压板附近.
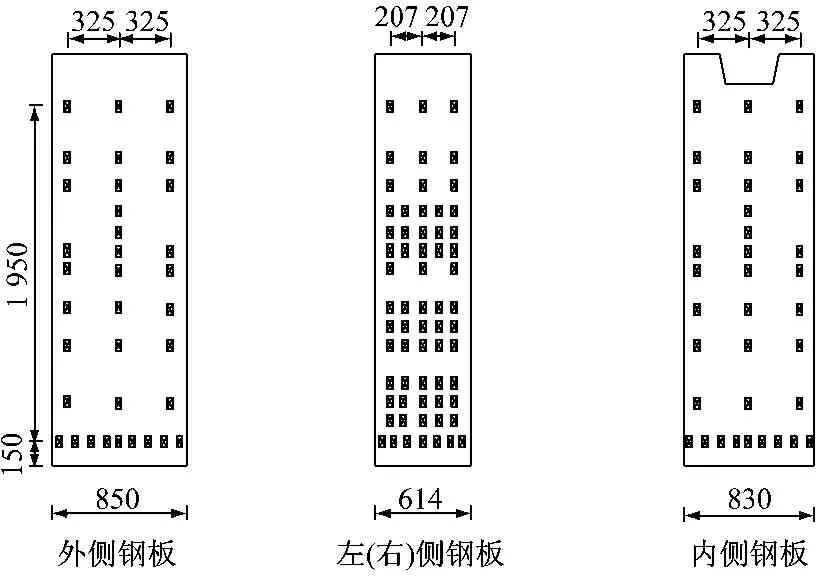
a 钢板应变测点
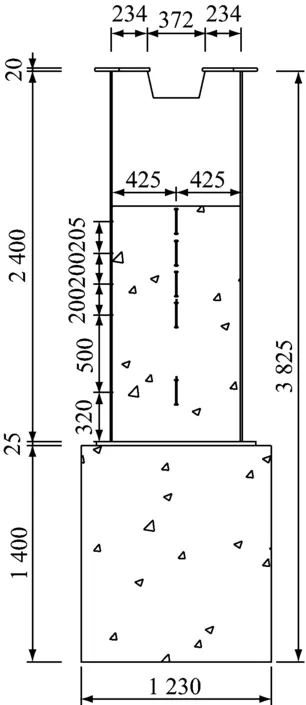
b 混凝土内正弦计测点
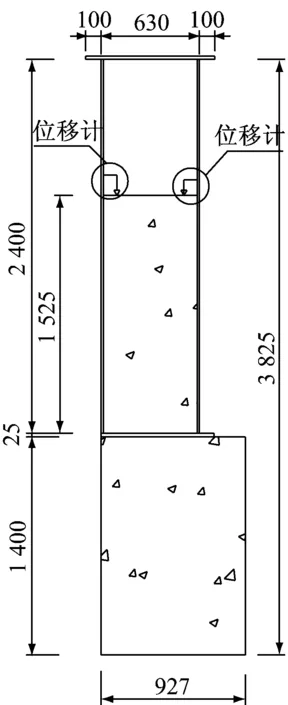
c 位移计测点图4 应变片布置(单位:mm)Fig.4 Layout of measuring points (unit: mm)

图5 前承压板式结合部钢结构应力分布
Fig.5Stressdistributionofsteelstructurewithfrontbearingplate
2.4 前承压板式结合部荷载滑移曲线
图7为结合部顶面钢和混凝土的相对滑移随荷载变化曲线.外侧钢板与混凝土的相对滑移要大于内侧,1.0P作用下外侧相对滑移为0.5 mm,内侧为0.1 mm;1.7P作用下,外侧为0.9 mm,内侧为0.2 mm.钢与混凝土相对滑移较小.这是由于承压板关于结合部底面形心不对称,内侧钢板所受约束较强引起的.
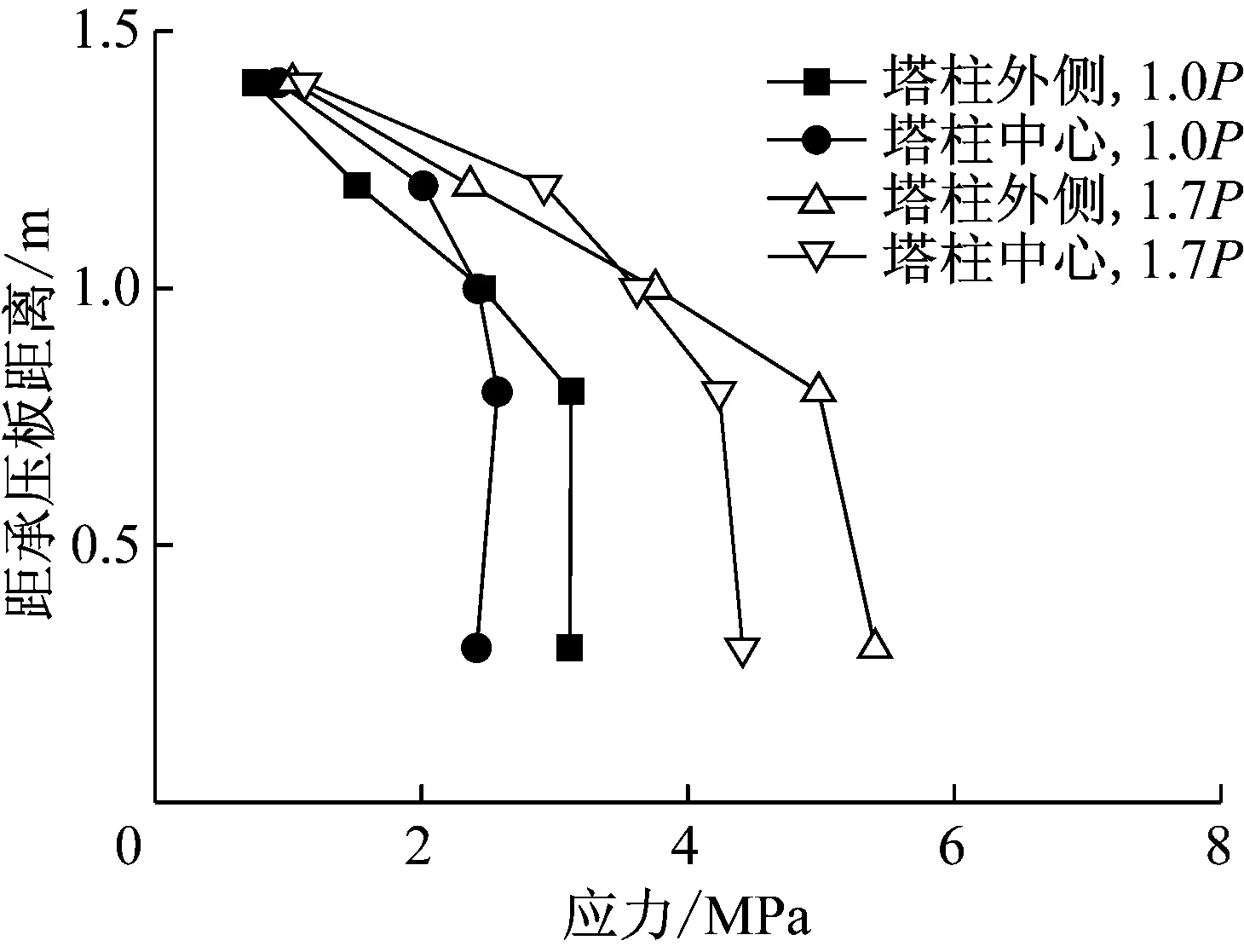
图6 前承压板式结合部混凝土结构应力分布
Fig.6Stressdistributionofconcretestructurewithfrontbearingplate

图7 前承压板式结合部荷载滑移曲线
Fig.7Load-slippagecurveofconnectionwithfrontbearingplate
2.5 前承压板式结合部钢混凝土轴力承担比例
在结合部底部接近承压板位置,钢结构承担的荷载比例即为承压板传力比.由图8可见,越靠近承压板,钢结构承担比例越小,混凝土承担比例越大.在承压板附近,混凝土承担荷载的比例约为60%,承压板传力比约为40%.随着荷载的增加,钢和混凝土各自承担的荷载没有发生明显变化.
3 后承压板式模型试验
3.1 后承压板式结合部构造
某桥塔钢-混凝土结合部如图9所示,结合部高4.7 m,位于最下端斜拉索锚固端下部,外壁板、钢腹板和加劲板将结合部分隔成17个钢格室.结合部端部设置一厚为60 mm的承压板.结合部加劲肋上开直径为75 mm的圆孔,并贯穿直径为25 mm的钢筋形成开孔板连接件,并在格室内钢板上焊接尺寸为Φ22 mm×200 mm的焊钉连接件,开孔板和焊钉连接件竖塔向间距为200 mm.焊钉和开孔板连接件通过承剪作用,承压板通过承压作用共同传递钢塔柱与混凝土塔柱间的作用力.
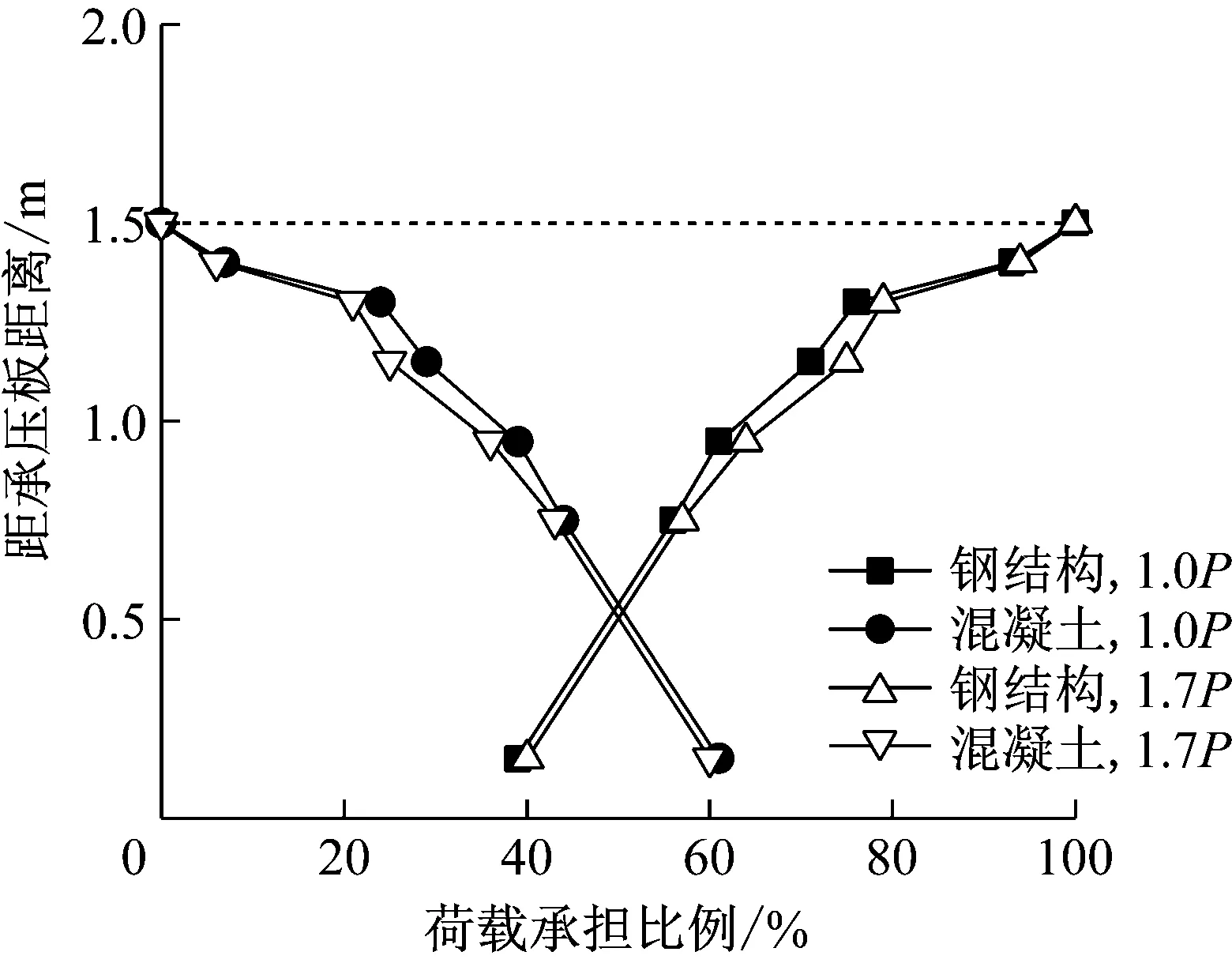
图8 前承压板式结合部荷载承担比例
Fig.8Loadproportionsharedbysteelandconcretestructurewithfrontbearingplate
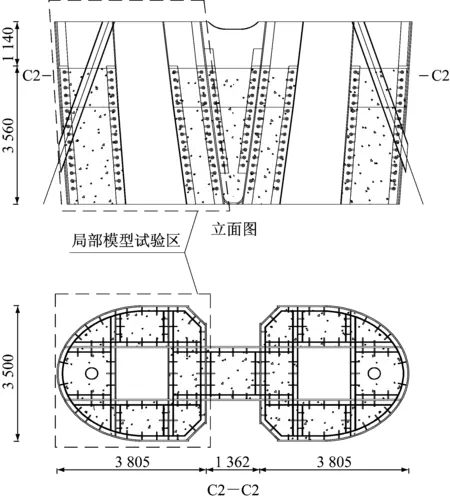
图9 后承压板式混合塔结合部构造(单位:mm)
Fig.9Structureofconnectionwithbackbearingplate(unit:mm)
选取单肢桥塔进行1∶3缩尺模型试验.钢板采用与实桥相同的Q345qD结构钢和相同等级的C55混凝土.承压板厚20 mm.开孔板和焊钉连接件按照塔竖向线刚度相似原则布置,截面内连接件数量与实桥一致.开孔板孔径为37.5 mm,孔中贯穿直径为13.0 mm的HRB335钢筋,焊钉连接件尺寸为Φ13 mm×80 mm,连接件沿塔竖向间距为100 mm.
根据等效应力换算,单肢桥塔结合部最不利工况下局部模型试验荷载P为6 500 kN,模型共进行2次往复加载,分别加载到1.0P和2.5P后卸载,加载等级为0.1P,加载之前先进行0.3P预加载,加载装置如图10所示.

图10 整体模型加载装置Fig.10 Load devices of overall model
模型测点布置如图11所示.格室钢板外侧布置应变测点,沿竖向每列设置7排.在钢格室内设置埋入式应变计,对混凝土内部应变进行测试,沿竖向共设置4排.结合部顶部设置千分表,测试钢与混凝土间相对滑移.
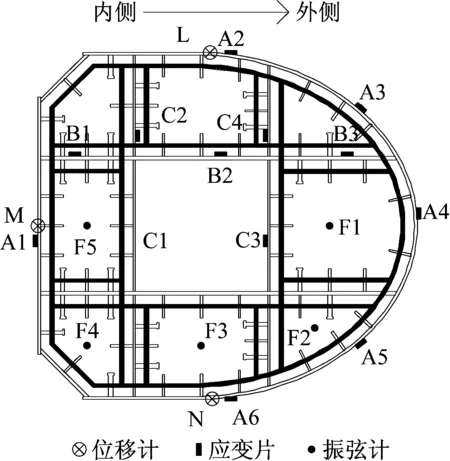
图11 测点平面布置Fig.11 Layout of measuring points
3.2 后承压板式结合部钢板应力
图12为1.0P和2.5P轴力作用下钢结构部分测点竖向正应力沿塔竖向分布曲线.随着距承压板距离的增加,钢板的竖向应力呈现出逐渐减小的趋势,在承压板附近钢板竖向应力衰减较快,承压板发挥了较好的承压作用.承压板以下钢结构竖向应力减少且趋势较为平缓,说明连接件传力较为平顺,传力效果较好.
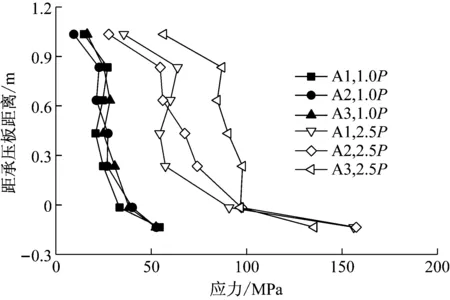
图12 后承压板式结合部钢结构应力分布
Fig.12Stressdistributionofsteelstructurewithbackbearingplate
3.3 后承压板式结合部混凝土应力
图13为1.0P和2.5P轴力作用下混凝土结构部分测点竖向正应力沿塔竖向分布曲线.混凝土结构的竖向应力从上往下呈现出逐渐增加的趋势,结合部通过承压板和连接件将钢板上的应力逐步传递给混凝土结构.靠近承压板位置混凝土应力增加较快,距承压板较远的区域混凝土应力增加的趋势逐渐减小.

图13 后承压板式结合部混凝土结构应力分布
Fig.13Stressdistributionofconcretestructurewithbackbearingplate
3.4 后承压板式结合部荷载滑移曲线
图14给出了结合部端部钢板与混凝土间的荷载-滑移曲线.1.0P轴力作用下端部3个位置处相对滑移数值分别为0.056、0.039、0.039 mm,数值较小,钢结构与混凝土结构变形协调,连接件具有足够的抗剪刚度将荷载传递给混凝土,钢结构与混凝土结构协作性能较好.2.5P轴力作用下最大滑移量为0.196、0.083、0.139 mm,表明连接件具有较高的安全储备.
3.5 后承压板式结合部钢混凝土轴力承担比例
图15给出了结合部各横截面钢和混凝土各自的荷载承担比例.越靠近承压板,钢结构承担比例越大,混凝土承担比例越小.由于承压板位于钢板第1排和第2排测点之间,两排测点位置钢结构分担的比例差即为承压板的传力比,其值约为40%.随着荷载的增加,钢和混凝土各自承担的荷载没有发生明显变化.
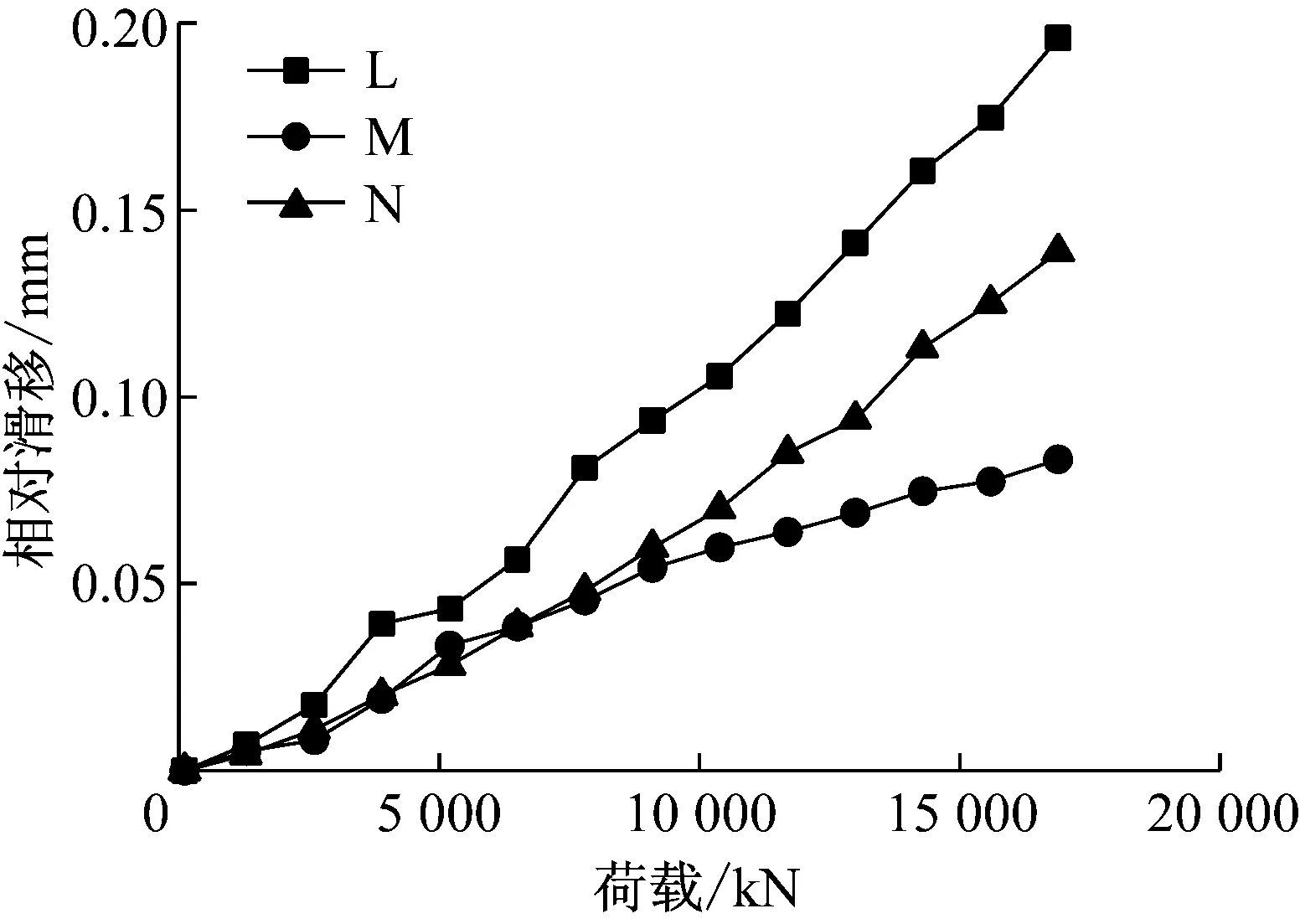
图14 后承压板式结合部荷载滑移曲线
Fig.14Load-slippagecurveofconnectionwithbackbearingplate
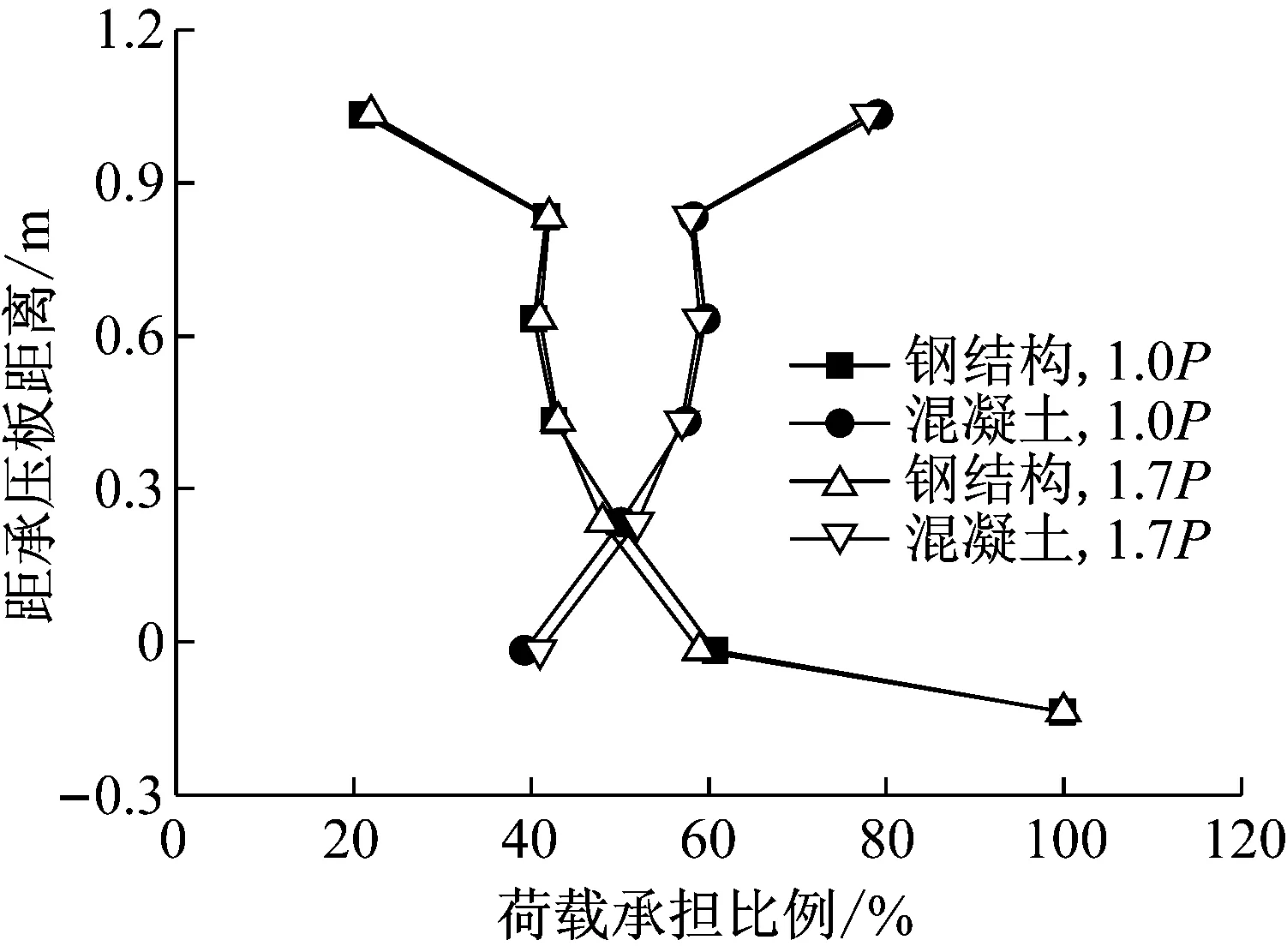
图15 后承压板式结合部荷载承担比例
Fig.15Loadproportionsharedbysteelandconcretestructurewithbackbearingplate
4 承压板对传力机理影响分析
4.1 钢结构应力
图16为1.0P荷载作用下前承压板式和后承压板式结合部钢板竖向应力平均值沿竖塔向分布.钢结构竖向应力从上往下均呈现出逐渐减小的趋势.前承压板式结合部钢板应力减小的趋势较为平缓;后承压板式结合部上部钢板应力减幅较大.这表明,后承压板式构造的承压传力效果更好,远离承压板区域钢结构应力过渡较为平缓.
4.2 混凝土应力
图17给出了1.0P荷载作用下前承压板式和后承压板式结合部混凝土竖向应力平均值沿竖塔向分布.混凝土结构竖向应力从上往下均呈现出逐渐增加的趋势.前承压板式结合部混凝土应力增加的趋势较为平缓;后承压板式结合部上部混凝土应力增幅较大.这表明,后承压板式构造的承压传力效果更好,远离承压板区域混凝土应力过渡较为平缓.
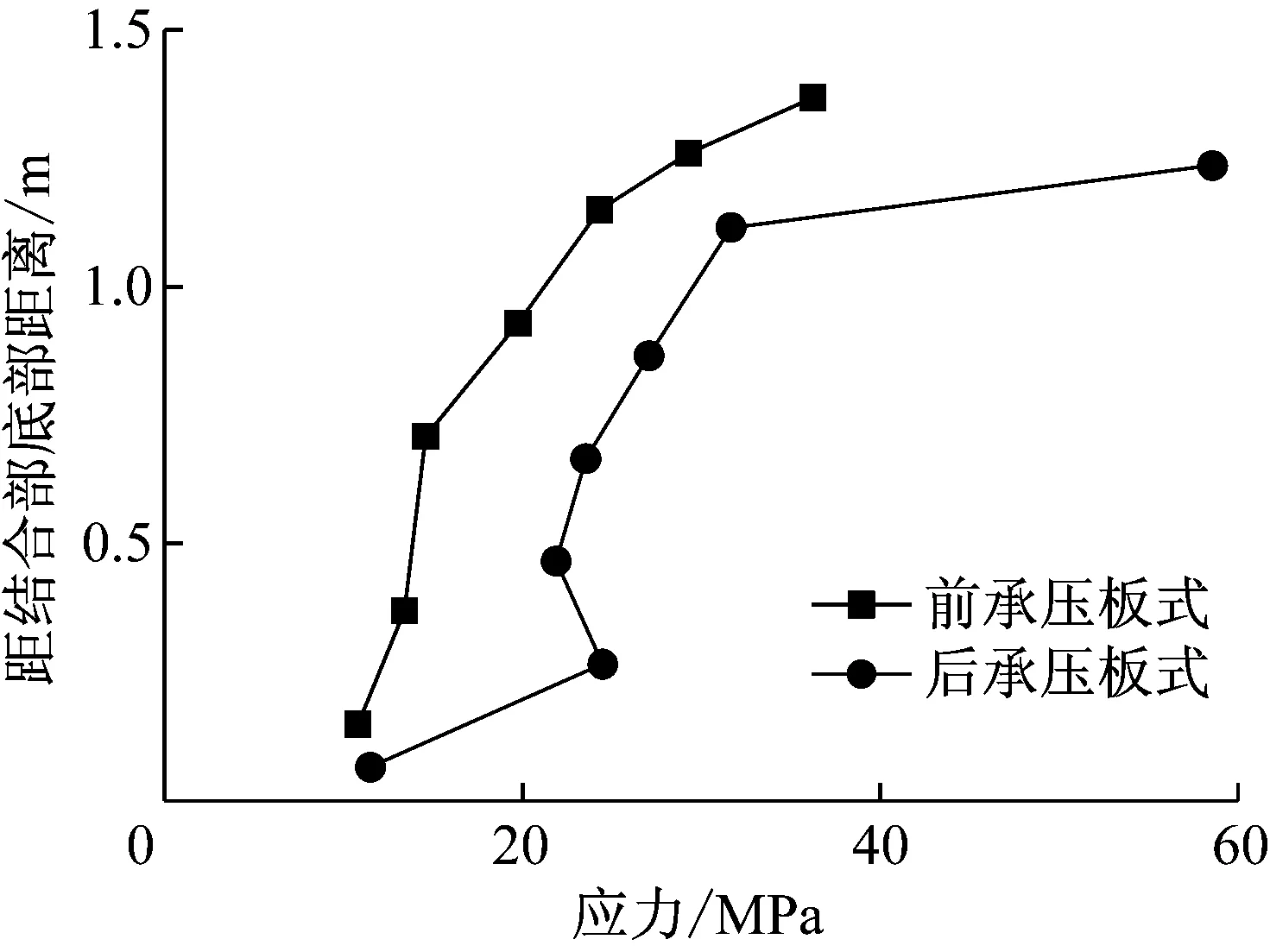
图16 承压板位置对钢板应力的影响Fig.16 Influence of bearing plate position on steel stress

图17 承压板位置对混凝土应力的影响Fig.17 Influence of bearing plate position onconcrete stress
4.3 连接件剪力
钢结构与混凝土结构通过剪力连接件传递荷载作用,因此钢结构截面合力的变化值,可近似为连接件剪力.图18为前承压板式结合部和后承压板式结合部连接件竖向剪力的分布状况.
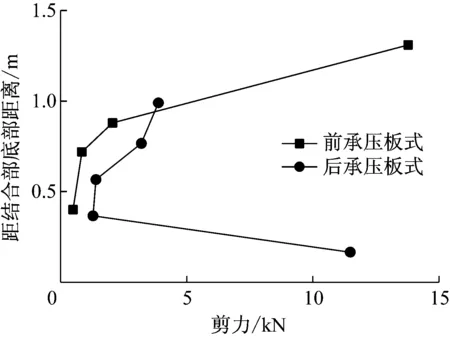
图18 承压板位置对承担比例的影响Fig.18 Influence of bearing plate position onsharing proportion
前承压板式结合部连接件竖向剪力从上往下呈现逐渐减小的趋势,1.0P荷载作用下连接件竖向剪力最大值为14 kN,结合部顶部连接件受力明显大于靠近承压板的连接件.前承压板式结合部,上部钢板应力较高而混凝土应力较低,连接件要抵抗二者间的应变差,作用剪力较大.随着力的传递,应变差逐渐减小,中部连接件作用力逐渐减小.在结合部下部由于前承压板的约束作用,钢板与混凝土应变差较小,故连接件剪力较小.
后承压板式结合部连接件剪力呈现出先减小再增大的趋势,1.0P荷载作用下连接件竖向剪力最大值为12 kN,后承压板式结合部底部连接件受力明显大于顶部连接件受力.后承压板式结合部顶部,由于受承压板约束,钢与混凝土之间相对变形较小,故连接件作用剪力较小.随着钢结构逐渐向混凝土结构传递荷载,混凝土应力逐渐增大,二者的相对变形逐渐增大,因此距离承压板较远处的连接件,剪力逐渐增大,在结合部底部连接件剪力达到最大值.连接件剪力分布较前承压板式构造更均匀.
5 结论
本文结合两座混合桥塔结合部模型承载性能模型试验,对前承压板式和后承压板式结合部传力机理进行了比较分析,得出如下结论:
(1)前承压板式结合部和后承压板式结合部均呈现出钢板应力从上往下逐渐减小,混凝土应力逐渐增加的趋势,钢塔柱应力较为平顺地传递给了混凝土塔柱,后承压板式构造承压传力效果更好.
(2)前承压板式和后承压板式结合部承压板传力比例均约为40%,说明前承压板式和后承压板式结合部均能充分利用承压板和连接件的复合传力作用,减小连接件的传力比例,使结合部受力更合理.
(3)由于承压板发挥较大作用,前、后承压板式结合部钢与混凝土间相对滑移较小,前承压板式结合部塔柱外侧钢板与混凝土相对滑移较内侧钢板与混凝土相对滑移稍大.
(4)前承压板式结合部连接件剪力从上往下逐渐减小,最上端连接件剪力最大;后承压板式结合部连接件剪力从上往下逐渐增加,最下端连接件剪力最大,剪力分布较前承压板式更均匀.
参考文献:
[1] 孙传洲. 捷克易北河玛丽安独塔斜拉桥 [J]. 世界桥梁,2000(2):36.
SUN Chuanzhou. The Marian Bridge, Czech Republic [J]. World Bridges, 2000(2):36.
[2] YUKIO A, AKIHIRO M. Study on connecting structure of main tower for Tsurumi Fairway Bridge[J]. Sumitomo Metals,1996,48(1):64.
[3] 陈开利,王戒躁, 安群慧. 舟山桃夭门大桥钢与混凝土结合段模型试验研究 [J]. 土木工程学报, 2006, 39(3):86.
CHEN Kaili, WANG Jiezao, AN Qunhui. Model tests on steel-concrete jointing section of main girder of a cable-stayed bridge [J]. China Civil Engineering Journal, 2006, 39(3):86.
[4] XIN Haohui, LIU Yuqing, HE Jun,etal. Experimental and analytical study on stiffened steel segment of hybrid structure [J]. Journal of Constructional Steel Research, 2014, 100(13):237.
[5] 卫星, 强士中. 斜拉桥桥塔钢-混凝土结合段传力机理试验研究 [J]. 工程力学, 2013, 30(1): 255.
WEI Xing, QIANG Shizhong. Specimen test for mechanics behavior of steel-concrete composite joint in pylon of cable-stayed bridge [J]. Engineering Mechanics, 2013, 30(1): 255. DOI: 10.6052/j.issn. 1000-4750. 2011. 06. 0351.
[6] 司秀勇, 肖林, 赵建波. 斜拉桥桥塔钢-混凝土结合段模型试验研究 [J]. 中国铁道科学, 2011, 32(5):26.
SI Xiuyong, XIAO Lin, ZHAO Jianbo. Model test research on steel-concrete joint section of cable-stayed bridge tower [J]. China Railway Science, 2011, 32(5):26.
[7] HE Jun, LIU Yuqing, PEI Bingzhi. Experimental study of the steel-concrete connection in hybrid cable-stayed bridges [J]. Journal of Performance of Constructed Facilities, 2014, 28(3):559.
[8] 张清华, 李乔, 唐亮. 桥塔钢-混凝土结合段剪力键破坏机理及极限承载力 [J]. 中国公路学报, 2007, 20(1):85.
ZHANG Qinghua, LI Qiao, TANG Liang. Fracture mechanism and ultimate carrying capacity of shear connectors applied for steel-concrete joint segment of bridge pylon [J]. China Journal of Highway and Transport, 2007,20(1):85.
[9] HE Shaohua, FANG Zhi, FANG Yawei,etal. Experimental study on perfobond strip connector in steel-concrete joints of hybrid bridges [J]. Journal of Constructional Steel Research, 2016,118:169.
[10] 郑双杰, 刘玉擎. 开孔板连接件初期抗剪刚度试验 [J]. 中国公路学报, 2014, 27(11):69.
ZHENG Shuangjie,LIU Yuqing. Experiment of initial shear stiffness of perfobond connector [J].China Journal of Highway and Transport, 2014,27(11):69.
[11] 蔺钊飞, 刘玉擎, 贺君. 焊钉连接件抗剪刚度计算方法研究 [J]. 工程力学, 2014(7):85.
LIN Zhaofei, LIU Yuqing, HE Jun.Research on calculation of shear stiffness for headed stud connectors [J]. Engineering Mechanics, 2014(7):85.

