基于角平分线的工程滑移索结构分析方法
于祥敏, 陈德伟, 白植舟, 洪能达
(1. 同济大学 土木工程学院, 上海 200092; 2. 宁波市江东阳光软件开发中心, 浙江 宁波 315040)
工程中经常用到滑轮与索形成的组合结构,其中一种为滑移索结构,即滑轮用于索结构的转向和支承,索可绕滑轮滑动直到达到平衡状态.滑移索结构中滑轮两边的索段长度会不断变化,其内力和变形的求解较复杂,常规的有限元方法不便于求解,仅有少量研究涉及到滑移索结构的有限元法分析[1-2].郭彦林等[2]提出了冷冻升温法,通过虚加温度荷载来调整滑轮两侧索单元的长度;Mcdonald等[3]建立了一种新单元模拟索在链杆连接的滑轮上滑动;唐建民等[4]通过推导索的滑移刚度矩阵来考虑索的滑移;Aufaure[5]采用附加广义自由度的方法以考虑索的滑移;魏建东等[6]采用二分法调整滑轮两侧索的无应力长度实现滑轮处索力连续性;彭伟贤等[7]提出了拉力分配法,即将不平衡拉力按相应的不平衡力分配系数进行分配,直到不平衡拉力为零;Ju等[8]提出一种超级单元模型以研究索绕多个滑轮的转动;Chung等[9]提出一种三维悬链线索单元考虑索的滑移效应;俞锋等[10]将索离散成相互联系的质点集合,通过质点运动描述索滑移.
针对滑移索结构,本文提出一种基于滑轮相邻索单元角平分线的简捷分析方法,可有效解决其分析复杂和困难的难题.计算示例和工程实例均验证了该方法的正确性和高效性.
1 基本假定
(1)索为理想柔性且满足虎克定律,始终处于弹性工作阶段.
(2)不计滑轮与索之间的摩擦力,即平衡状态滑轮两侧的索力大小相等.
(3)滑轮半径是小量,不计滑轮半径的影响,将其简化为一个点.
2 计算原理
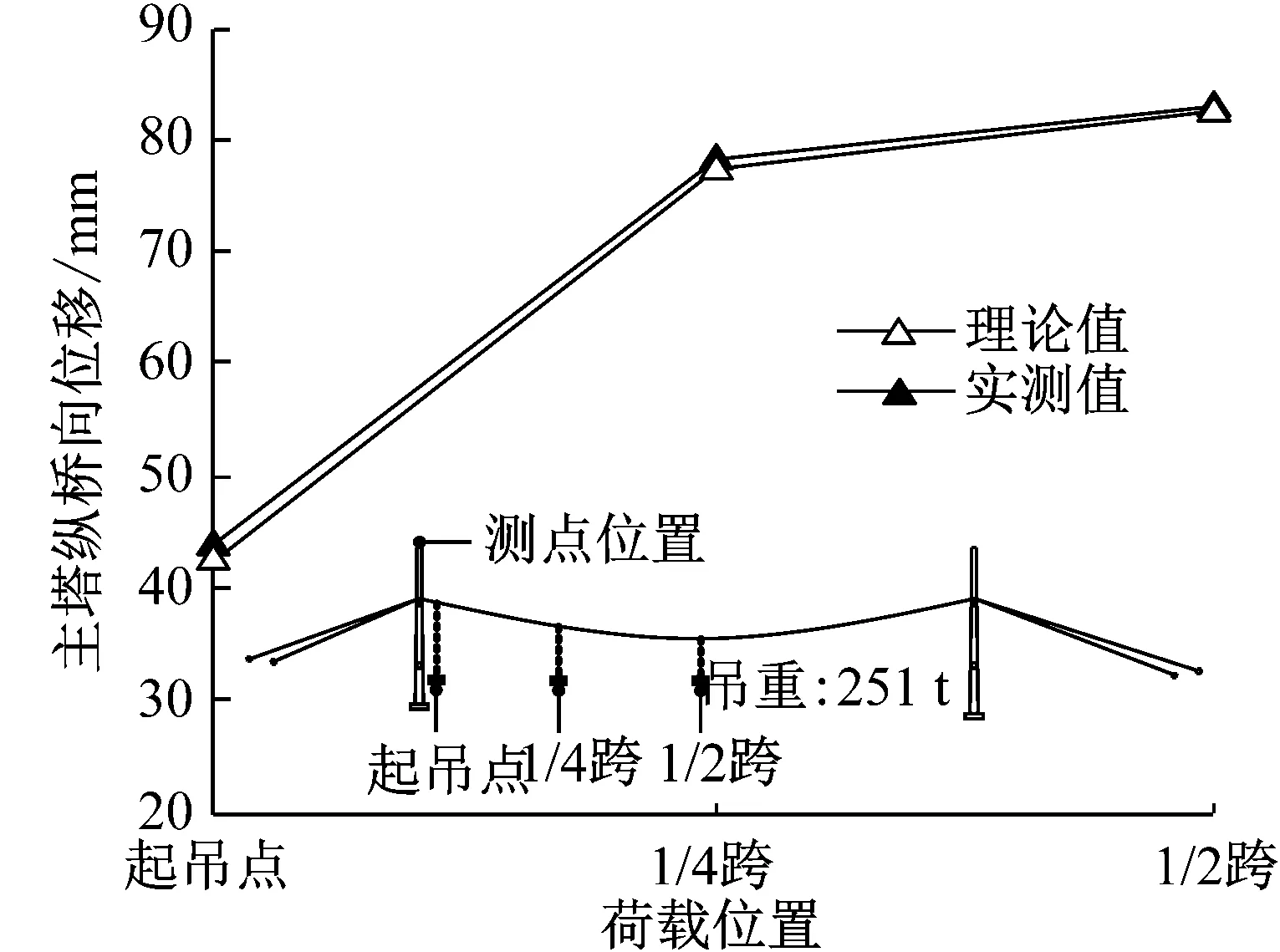
对于如图1a所示滑移索结构,当绕过滑轮的索在两侧存在不平衡力F1、F2时(假定F1 a 滑移索结构 b 简化模型图1 滑移索结构及简化分析模型Fig.1 Sliding cable structure and simplified model 采用多段杆单元模拟索,采用固定铰模拟滑轮对索的约束作用,简化模型如图1b所示.其中,O点为滑轮邻近索单元的切线交点;α1、α2为滑轮处相邻索单元的水平夹角;β为滑轮处相邻索单元角平分线的方向角;F1、F2为滑轮处相邻索单元的最终索力,平衡状态时F1=F2.为叙述方便,后文将沿角平分线方向的约束反力简称为径向反力,而垂直于角平分线方向的约束反力简称切向反力.平衡状态下固定铰约束力作用方向与相邻索单元的角平分线重合,因此其切向反力为零. 滑移索结构中索单元所承受的自重和外荷载不会改变索的无应力长度,只有给索单元主动施加的索力会改变其无应力长度[12].在滑移索结构有限元分析时,滑轮对索的约束作用简化为一固定铰.当索绕滑轮滑动时(假设左侧索滑入右侧索时滑轮处无应力索长调整量为正,反之为负),当该滑动作用导致左侧索无应力长度缩短ΔL时,右侧索无应力长度将增长ΔL,显然通长索整体的无应力长度依然保持恒定. 当该滑轮处无应力长度调整量为单位长度时(即ΔL=1),索主动施加的初始索力变化(即名义索力)为 (1) 式中:L1和L2分别为左侧和右侧索的无应力索长;E和A分别为索的弹性模量和有效截面积. 在新荷载作用下,问题的求解最后归结为每个滑轮处无应力长度调整量,未知数个数即为滑轮数量.本文采用影响矩阵法求解,即 Ftar=Mf+Fcon (2) 式中:M为滑轮无应力长度调整影响矩阵,其子元素Mij代表j滑轮无应力长度调整量为单位长度时产生的i处滑轮切向反力,显然,当i、j为非相邻滑轮时,该子元素为零;f为滑轮无应力长度调整量向量,属于需要求解的未知数;Fcon为自重和外荷载等固定荷载作用下滑轮切向反力向量;Ftar为零向量,即所有滑轮处滑轮切向反力为零,由此满足索力连续性.求解方程(2)即可得到滑轮无应力长度调整量向量. 在求解得到各滑轮处无应力调整量后,仿照公式(1)对各子索主动施加的初始索力进行调整,施加自重和外荷载即可计算得到无应力长度调整后各子索的线形和内力. 角平分线法的流程如图2所示,具体步骤如下: (1)建立滑移索结构的有限元模型. (2)对每根索施加公式(1)的索力变化量,求解得到滑轮单位无应力长度调整影响矩阵M,求解方程(2)得到滑轮无应力长度调整量. (3)重新计算各子索的线形,调整滑轮两侧索单元角平分线的方向角,按照步骤(2)重新计算,重复至全部子索的线形和内力收敛. 为方便起见,图2流程图仅仅列出以角平分线方向角收敛(即索的线形)为判断准则,实际计算可同时应用索力收敛判断,即采用线形和内力双控作为收敛判断准则. 图2 角平分线法流程图Fig.2 Flowchart of angle bisector method 滑移索结构的算例1如图3所示,索单元总无应力长度为150 m,其中左边索的无应力长度L1=50 m,角度为45°,划分为16个单元;右边索无应力长度L2=100 m,角度为15°,划分为32个单元.索单元截面积均为A=0.017 48 m2,弹性模量E=195 GPa,自重γ=96 kN·m-3. 图3 算例1Fig.3 Sample 1 由于该算例的滑移索结构只有1个滑轮,因此其影响矩阵M为1阶,即1个数值.算例1迭代过程的关键结果列于表1,其中“影响矩阵”和“无应力索长调整量”栏均为当前行“角平分线方向角”对应的求解值;“最终索力”栏为考虑各子索无应力索长调整后的求解值,下一行的“角平分线方向角”即为该行“最终索力”作用下结构的变形结果. 由表1可知:①影响矩阵M随着索形的变化在迭代过程中不断更新.②迭代过程中,在无应力索长调整后的基础上计算索力,可以发现滑轮处左右侧索力将存在不闭合误差.该不闭合误差随着迭代的进行不断收敛,4步迭代后不闭合误差仅为0.002%.③迭代过程中角平分线方向角同样很快收敛,4步前后误差仅为0.012%,略慢于索力不闭合误差的收敛速度. 文献[2]的算例为工型截面悬臂钢梁,通过一根跨过滑轮的钢索悬挂,其中作用于钢梁上的均布荷载为3.16 kN·m-1,如图4所示.索和钢梁的弹性模量分别为180 GPa和210 GPa,面积分别为3.65 cm2和33.36 cm2.采用本文提出的角平分线法进行索滑移的模拟,并与文献[2]中的冷冻升温法进行对比,计算结果见表2.由表2可知:角平分线法与冷冻升温法相比,索力不闭合误差更小,收敛速度更快,二者计算结果吻合很好. 图4 斜拉梁算例(单位:mm)Fig.4 Cable-stayed beam(unit: mm)表1 算例1迭代过程Tab.1 Iteration process for sample 1 迭代次数α/(°)116单元117单元β/(°)βi-βi-1βi()%M/kN无应力索长/m最终索力/kN调整量总长度116单元117单元最终索力不闭合误差/%145.00015.000105.00039321.5400.01584121501380.2811412.0182.248246.16418.203103.9810.98039439.8190.01633041501406.3291407.2380.065346.14218.214103.9640.01639441.5970.01632431501406.7681407.1590.028446.13018.226103.9520.01239442.8330.01632011501407.0771407.1030.002 表2 算例2结果比较Tab.2 Result comparison for sample 2 贵黔高速上的鸭池河特大桥为主跨800 m的混合梁斜拉桥,主跨为钢桁梁,边跨为预应力混凝土梁,其中主跨钢桁梁采用缆索吊机悬臂拼装施工[13].缆索吊机设计起吊能力为350 t,单侧主缆由12根Φ60 mm钢丝绳组成,左边和右边主缆水平投影长度分别为(208.6+800.0+323.1)m、(243.2+800.0+287.4)m,如图5所示. 缆索吊机的索鞍为典型的滑移索结构,主要由定滑轮组和钢框架组成.索鞍固定在主塔横梁上,主缆可绕滑轮滑动.为验证缆索吊机的性能,缆索吊机在投入使用前进行了试吊试验.试验过程中,缆索吊机将251 t试验荷载从贵阳岸的起吊点运送到黔西岸卸载,期间测量了主缆力和主塔位移. 图5 工程实例(单位:m)Fig.5 Application to engineering (unit: m) 采用本文提出的方法进行缆索吊机仿真分析,有限元模型及单元编号如图6所示,其中主塔和主缆分别采用梁单元和多段杆单元模拟,主缆面积为A=0.001 824 m2,弹性模量为E=195 GPa.该缆索吊机每侧主缆有2个滑轮,全桥共4个滑轮,因此其影响矩阵M为4×4阶方阵.迭代过程采用线形和索力双控,误差控制精度均设为δ=0.05%. 首先根据设计空缆线形确定主缆的无应力长度和索力,即确定结构的初始平衡状态.试验过程中荷载从贵阳岸移动到黔西岸,加载点和计算工况较多,但分析过程相似.本文仅给出251 t试验荷载位于跨中位置的迭代过程,详见表3.由表3可知:仅2次迭代即可达到滑轮两侧的索力不闭合误差均小于0.05%的精度,计算效率很高.最后输出主缆力和主塔位移等结果并与荷载试验的现场实测值进行对比,如图7所示.从图7可以看出:缆索吊机的数值分析结果与现场实测值吻合较好,二者误差小于3.5%,验证了本文提出方法的正确性和可行性. 表3 荷载位于跨中的迭代计算Tab.3 Iteration process for test load at mid-span 图6 缆索吊机有限元模型及单元编号Fig.6 Finite element model for cable crane andelement number a 主缆力 b 主塔位移图7 荷载试验结果Fig.7 Results of load test 滑移索结构中,由于索可绕滑轮滑动,因此求解其内力和变形非常复杂.本文提出一种基于角平分线和无应力长度调整影响矩阵的简捷分析方法,并以计算示例和工程实例进行验证.该方法具有力学概念清晰、计算效率高等优点,文中算例仅需要2~4次迭代即可达到很高精度的收敛解. 参考文献: [1] 张立新, 沈祖炎. 预应力索结构中的索单元数值模型[J]. 空间结构, 2000, 6(2): 18. ZHANG Lixin, SHEN Zuyan. Numerical model of prestressed cable element in cable structure [J]. Spatial Structures, 2000, 6(2): 18. [2] 郭彦林, 崔晓强. 滑动索系结构的统一分析方法——冷冻-升温法[J]. 工程力学, 2003, 20(4): 156. GUO Yanlin, CUI Xiaoqiang. An unified analytical method for gliding cable structures-frozen-heated method [J]. Engineering Mechanics, 2003, 20(4): 156. [3] MCDONALD B M, PEYROT A H. Analysis of cables suspended in sheaves [J]. Journal of Structural Engineering, ASCE, 1988, 114(3): 693. [4] 唐建民, 沈祖炎. 悬索结构非线性分析的滑移索单元法[J]. 计算力学学报, 1999, 16(2): 17. TANG Jianmin, SHEN Zuyan. Sliding cable element method for nonlinear analysis of cable structure [J]. Chinese Journal of Computational Mechanics, 1999, 16(2): 17. [5] AUFAURE M. A three node element ensuring the continuity of the horizontal tension a clamp cable element [J]. Computers & Structures, 2000, 7(4): 243. [6] 魏建东, 刘忠玉. 一种连续索滑移的处理方法[J]. 计算力学学报, 2003, 20(4): 495. WEI Jiandong, LIU Zhongyu. A method of continuous slipping cable [J]. Chinese Journal of Computational Mechanics, 2003, 20(4): 495. [7] 彭伟贤, 陈春雷, 梁佶, 等. 一种滑移索的简捷计算方法[J]. 结构工程师, 2005, 21(1): 30. PENG Weixian, CHEN Chunlei, LIANG Ji,etal. A simplified calculation method for dealing with sliding cable [J]. Structural Engineers, 2005, 21(1): 30. [8] JU F, CHOO Y S. Super element approach to cable passing through multiple pulleys [J]. International Journal of Solids and Structures, 2005, 42(11): 3533. [9] CHUNG K, CHO J, PARK J,etal. Three-dimensional elastic catenary cable element considering sliding effect [J]. Journal of Engineering Mechanics, ASCE, 2011, 137(4): 276. [10] 俞锋, 罗尧治. 索杆结构中索滑移行为分析的有限质点法[J]. 工程力学, 2015, 32(6): 109. YU Feng, LUO Yaozhi. The finite particle method for analysing cable sliding in cable-strut structures [J]. Engineering Mechanics, 2015, 32 (6): 109. [11] 赵朝阳, 杨文爽, 李传习, 等. 缆索吊装主索系统的受力分析算法与工作性能[J]. 广西大学学报(自然科学版), 2010, 35(4): 615. ZHAO Chaoyang, YANG Wenshuang, LI Chuanxi,etal. Study on static analysis and working performance of the main cable system in the cable-hoisting system [J]. Journal of Guangxi University (Natural Science), 2010, 35(4): 615. [12] 秦顺全. 斜拉桥安装无应力状态控制法[J]. 桥梁建设, 2003, 33(2): 31. QIN Shunquan. Control method of stress-free status for erection of cable-stayed bridges [J]. Bridge Construction, 2003, 33 (2): 31. [13] 于祥敏, 陈德伟, 白植舟, 等. 贵黔高速鸭池河特大桥钢桁梁施工关键技术 [J]. 桥梁建设,2017, 47(4): 107.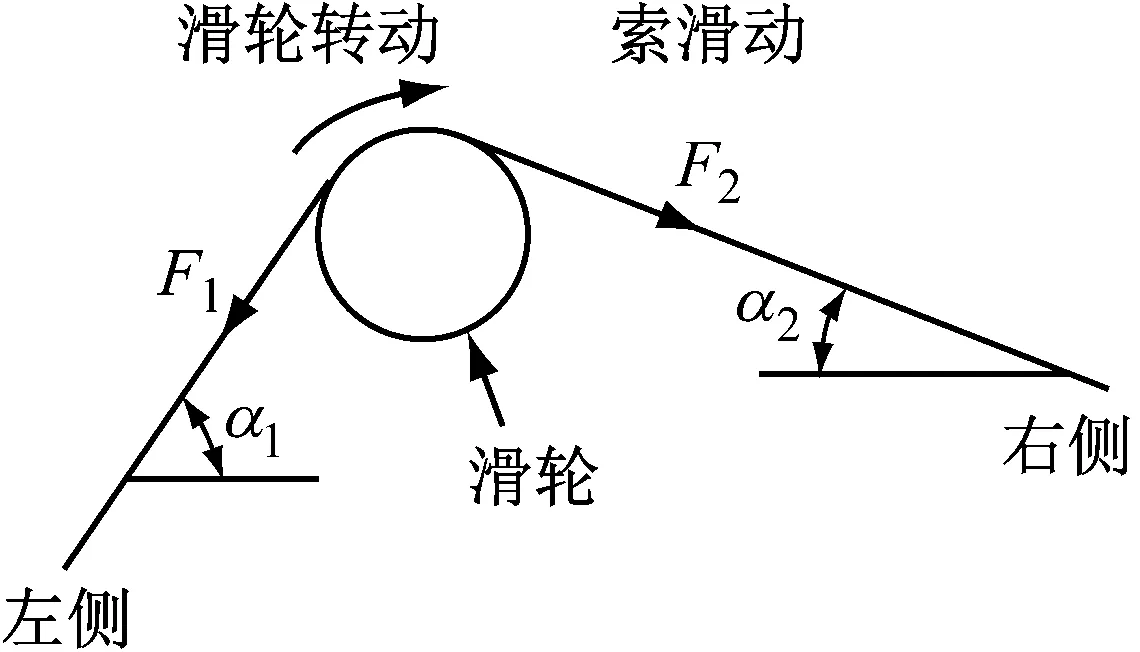
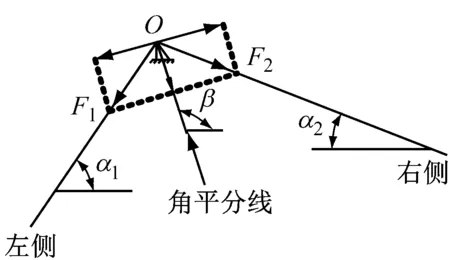
3 计算方法
3.1 无应力长度调整影响矩阵M
3.2 角平分线法迭代过程

4 计算示例
4.1 算例1

4.2 算例2



5 工程实例

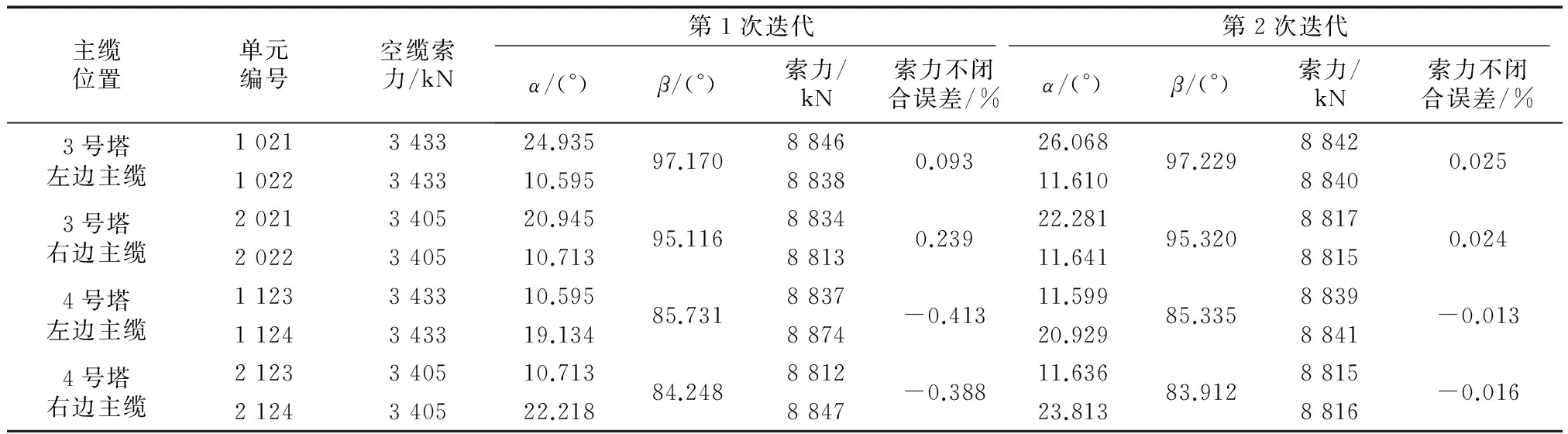
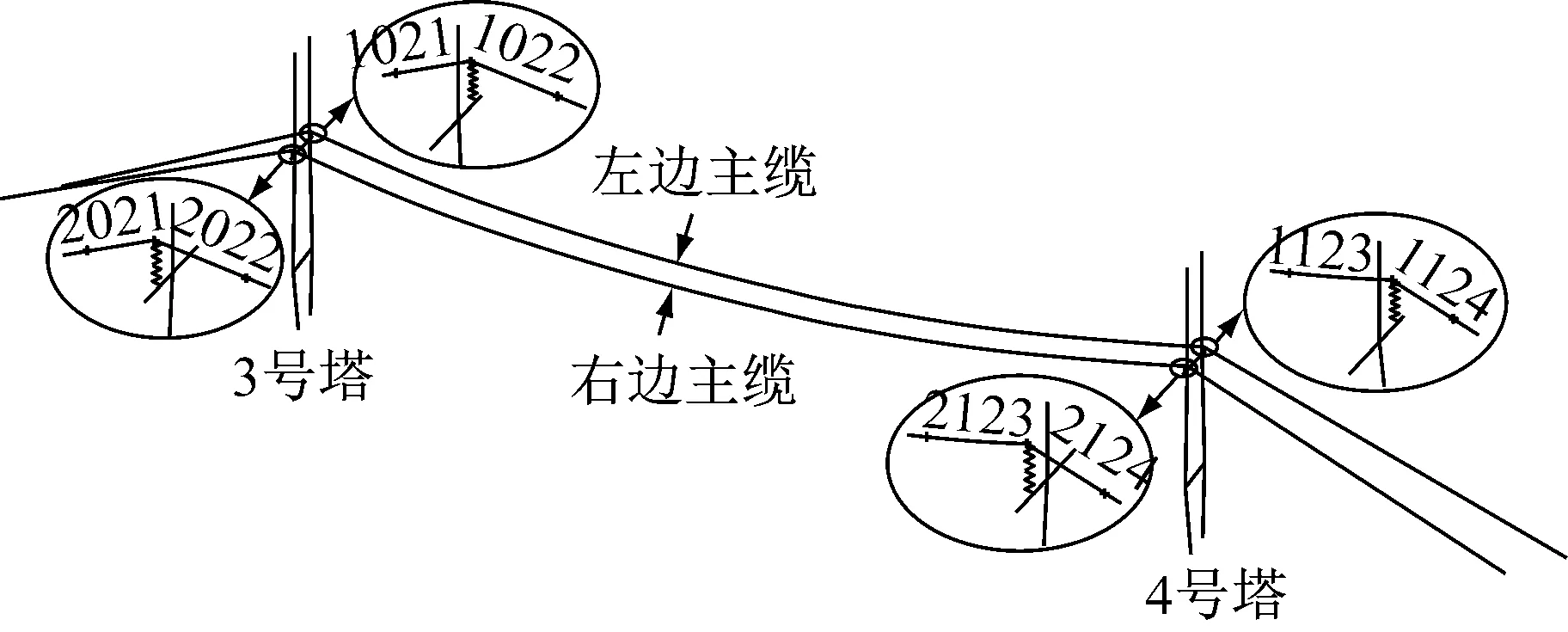

6 结 语


