基于Hilbert-Huang变换的软性磨粒流抛光流道压力脉动分析*

计时鸣，李 军,2，谭大鹏*

(1.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014；2.杭州师范大学 信息科学与工程学院，浙江 杭州 311121)

0 引 言

随着先进制造业的迅速发展，精密超精密机械零件的需求剧增。同时，随着机械零件的结构化表面(孔、槽、沟、窄缝等复杂异形表面的统称)越来越复杂，利用目前的光整加工方法如磁性磨粒加工(magnetic abrasive finishing, MAF)、磁流变抛光(magnetorheological finishing, MRF)、液体射流抛光(fluid jet polishing, FJP)等[1-2]已经无法达到抛光精度要求。这些方法利用了磨粒流良好的仿形性，通过对磨粒流施加强大的挤压力或喷射力实现对结构化表面的冲击碰撞或刮削。但在磨粒流的强力作用下，加工表面也留下了具有明显方向性的加工纹理，因此较难实现高精度抛光。

针对现有磨粒流加工存在的不足，浙江工业大学计时鸣等[3-5]提出基于“软性”磨粒流的镜面级加工新方法，利用约束模块和结构化表面构建约束流道，让湍流状态下的低黏度的磨粒流循环进入约束流道，使得磨粒与加工表面进行频繁地微量微力切削，从而实现了结构化表面的镜面级加工。新方法镜面抛光效果明显的，但是加工效率不高、抛光不够均匀等问题仍需课题组深入研究，因此，课题组进行了改变约束模块结构[6]、约束流道加工工艺参数优化[7]、软性磨粒流壁面特性分析[8]、引入超声激振强化湍流[9]等一系列研究和实验，改进和优化了原有的抛光方法，在加工效率、抛光均匀性等方面有所改善和提高。

约束流道中的固液两相磨粒流湍流发展是决定光整加工效果的关键因素，而流道内压力脉动信号承载着湍流发展的大量信息[10]，本文在上述研究基础上，以约束流道内压力脉动特性为研究对象，用Hilbert-Huang变换(HHT)时频分析工具，研究约束流道内的湍流发展与压力脉动信号的内在联系，以期通过压力脉动信号的监测和时频分析，对流道内的湍流进行调控。

1 HHT变换原理

HHT是1998年由Huang等[11]提出的一种适用于非线性非平稳信号的时频分析方法，包括经验模态分解(EMD)和Hilbert变换(HT)。HHT变换的核心是EMD分解，EMD分解得到的IMF函数必须满足两个条件：①IMF函数的过零点和极值点个数必须相等或者相差一个；②IMF函数的局部极小值构成的包络线和局部极大值构成的包络线平均值为零。

假设被分析信号为x(t)，进行EMD分解后：

(1)

被分析信号x(t)被分解成n个IMF函数c(t)和残余分量rn(t)，对每个IMF函数ci(t)进行Hilbert变换:

(2)

从而得到对每个IMF函数的解析信号：

zi(t)=ci(t)+jdi(t)

(3)

进而求得每个IMF函数的幅值函数和相位函数：

(4)

(5)

最后，根据瞬时频率是某一时刻相位的导数关系，得出每个IMF的瞬时频率：

(6)

从而每个IMF的Hilbert谱是：

(7)

式中:Re—取实部同时忽悠残余项，Hilbert谱反应了瞬时频率与幅值随时间的变化规律。

对Hilbert谱进行积分可以得到HHT边际谱：

(8)

2 软性磨粒流动力学模型

在软性磨粒流加工中，固液两相流被认为是不可压缩流体，因此磨粒流的密度为常数，其连续性方程：

(9)

式中：ux，uy，uz—笛卡尔坐标系中的X，Y，Z轴3个方向上的速度。

由于在磨粒流加工需要考虑剪切力的作用，本研究使用微元体控制方法对微元体进行受力分析，得到黏性流体运动微分方程，同时结合广义牛顿内摩擦定律关于法向应力的3个方程和切应力的3个补充方程推导出纳维尔-斯托克斯(Navier-Stokes)方程：

(10)

式中：p—应力张量，Pa；ρ—流体密度，kg/m3；ν—流体的运动黏性系数，m2/s；fi—质量力，N；t—时间，s；xi，xj—两个坐标方向的张量表示，m。

湍流中各物理量都具有某种统计特征的规律，因此基本方程中任一瞬间物理量都可用平均物理量和脉动物理量之和来代替，并且可以对整个方程进行时间平均的运算，经过时间平均的连续方程和N-S方程称为雷诺方程：

(11)

(12)

式中：ui，uj—两个坐标方向的速度张量表示，m/s。

式中出现了雷诺应力项，导致该方程不封闭，实际使用时需要根据不同应用场合选用相应的数学模型设定参数，同时假设一些条件让方程封闭。

将式(9，10)分别减去式(11，12)就可得到脉动运动方程和脉动运动连续方程。

本文选用了可实现k-ε湍流模型进行仿真求解，Realizable模型相对Standard模型来说，最大的区别是把湍动粘度计算式中的模型系数Cμ作为变量处理，从而可以更加准确地对软性磨粒流进行数值模拟。

3 数值计算分析

3.1 物理模型

本研究设计制作了矩形约束流道的加工装置，为了减少计算时间和简化建模过程，笔者对实际加工装置进行了适当的简化，矩形约束流道简化模型如图1所示。

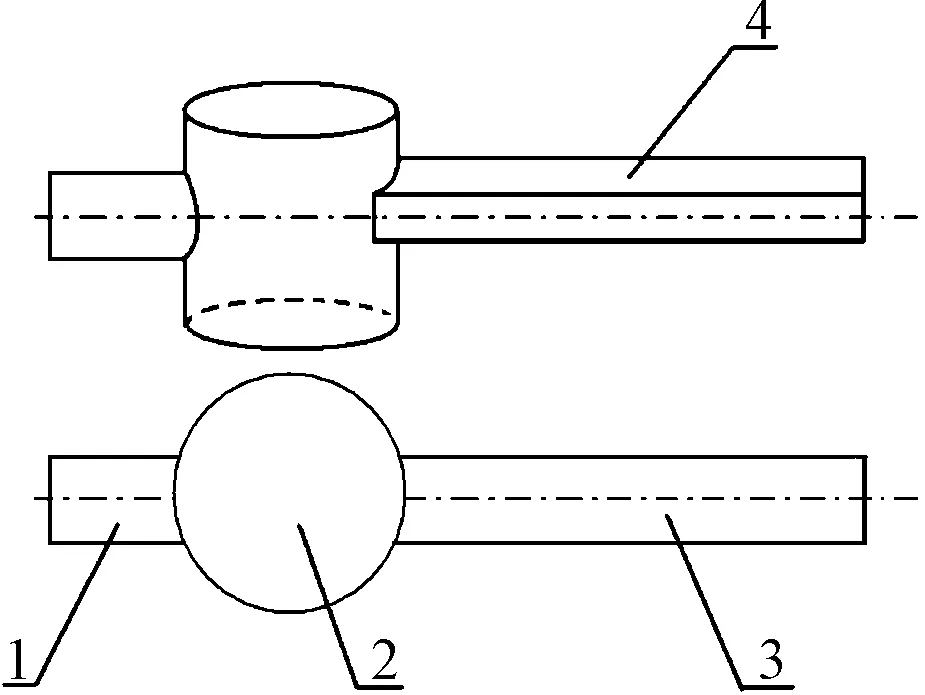
图1 矩形约束流道简化模型1—圆形进口；2—湍流发生器；3—矩形约束流道；4—矩形流道上表面

图1中，矩形流道的出口直接与连接管相通，由于出口湍流为完全发展条件，可以忽略对矩形约束流道内磨粒流流态特性的影响。

3.2 网格划分和参数设置

本研究采用分块方式对模型进行网格划分，共划分出726 300个大小为0.1的网格单元，划分示意图如图2所示。

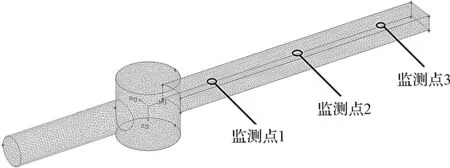
图2 矩形约束流道网格划分

根据磨粒流“软性”的要求，磨粒流固相是SiC颗粒，液相由水、切削液和分散剂按一定比例配制的混合液体。约束流道内磨粒流具体参数设置如表1所示。

表1 约束流道内磨粒流参数设置

数值计算中，约束流道的入口边界设成速度入口(Velocity-inlet)，速度变化采用UDF自定义函数的方式输入，出口设成自由出口(outflow)，壁面处设成无滑移壁面边界条。文献[9]中提出的采用超声激振对强化湍流的效果是明显的，因此，本文在构建入口速度函数时，依然采用超声波频段的速度波动函数，同时考虑流道内的状态应该是非线性非平稳的复杂信号，混合了20 kHz、30 kHz、40kHz、50 kHz、25 kHz、35 kHz、45 kHz等多种时变频率的成分。

同时，为了观测软性磨粒流在约束流道中随入口速度的非线性非平稳变化，各个参数的动态变化，本研究选用可实现k-ε湍流模型、非定常(unsteady)求解方式进行计算，为了获得压力脉动信号，本研究在约束流道的上表面设置了3个压力监测点，笔者将监测数据保存到本地，以便进行HHT分析。考虑到构建的入口速度函数的最高频率为50 kHz，根据信号采样定理，采样频率至少要100 kHz以上，因此计算时间步长设为0.000 005 s，时间步为2 048步。流体运动的物理时间为0.010 24 s，足够达到稳定状态。

3.3 数值模拟结果分析

本研究通过数值模拟获得了压力监测点的静态压力数据，而压力脉动p*的公式[12-15]如下：

(14)

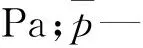
根据数值模拟结果和公式(14)得到了监测点1、监测点2、监测点3的压力脉动的时域波形，分别如图(3～5)所示。

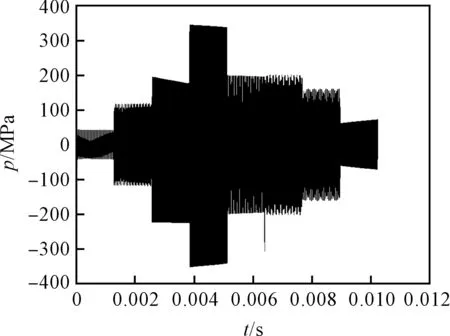
图3 监测点1压力脉动时域波形

图4 监测点2压力脉动时域波形

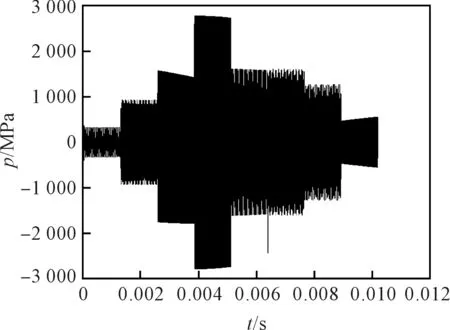
图5 监测点3压力脉动时域波形

从图(3～5)中可看出，压力脉动信号从监测点1到监测点3的幅度逐渐增大。

为了获得更多的软性磨粒流流道内的压力变化信息，本研究对监测点1的时域信号进行EMD分解，分解结果如图6所示。

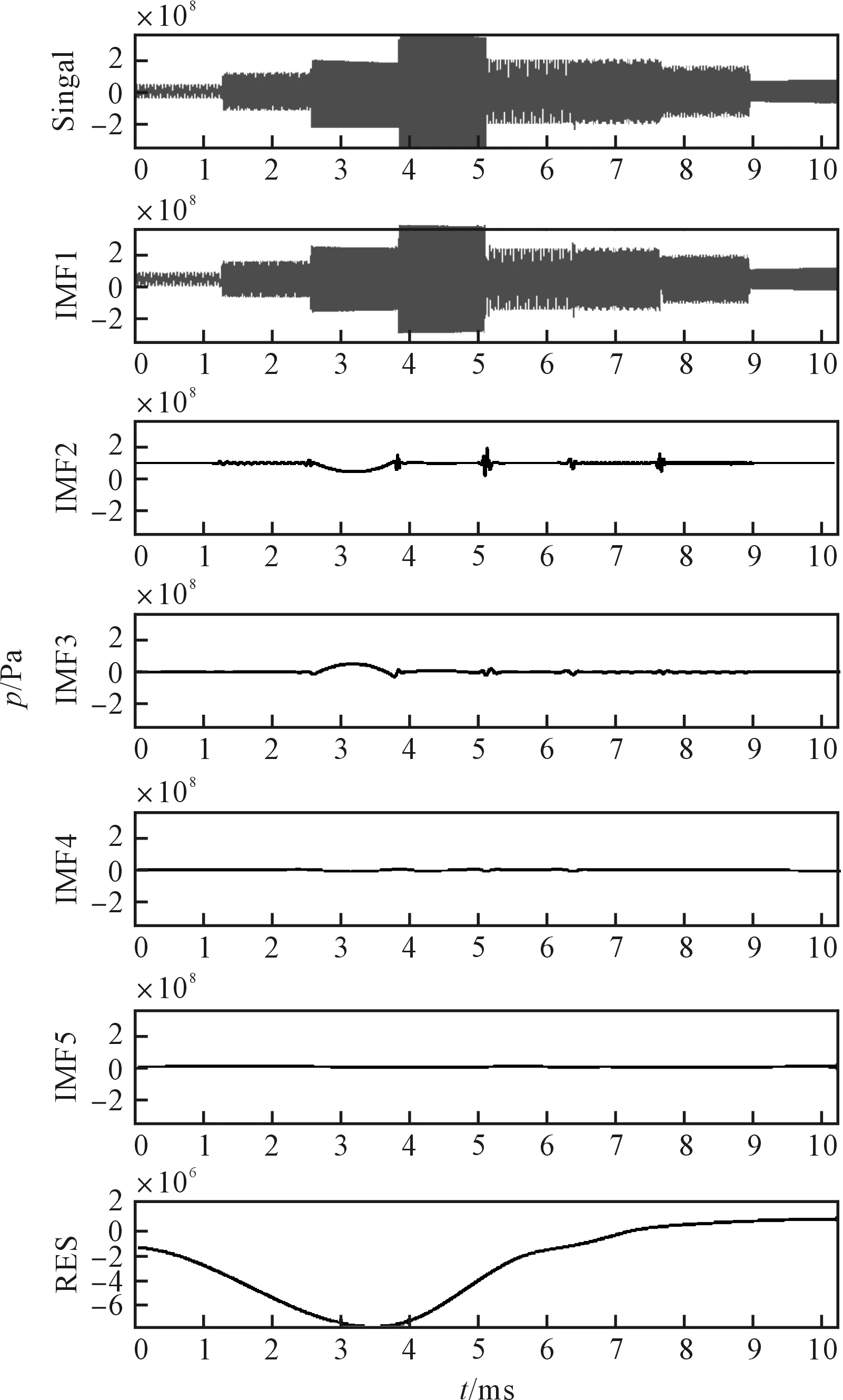
图6 检测点1压力脉动信号EMD分解结果

本研究根据图6中的每个IMF分量可以获得压力脉动的Hilbert谱，对Hilbert谱进行积分可以得到希尔伯特_黄变换(HHT)边际谱，如图7所示。

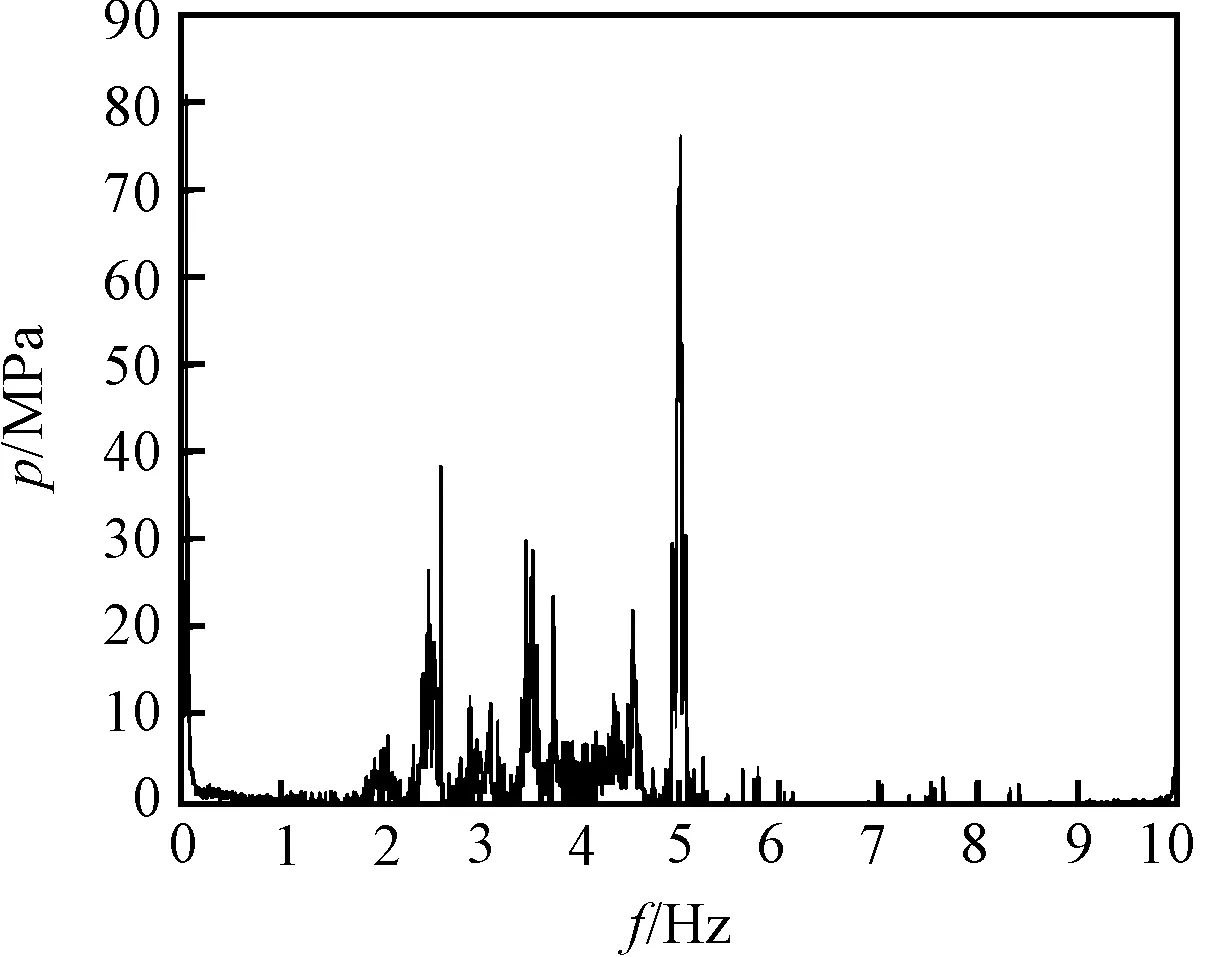
图7 检测点1 HHT变换边际谱

同理，可得监测点2和监测点3的HHT变换边际谱，分别如图8、图9所示。

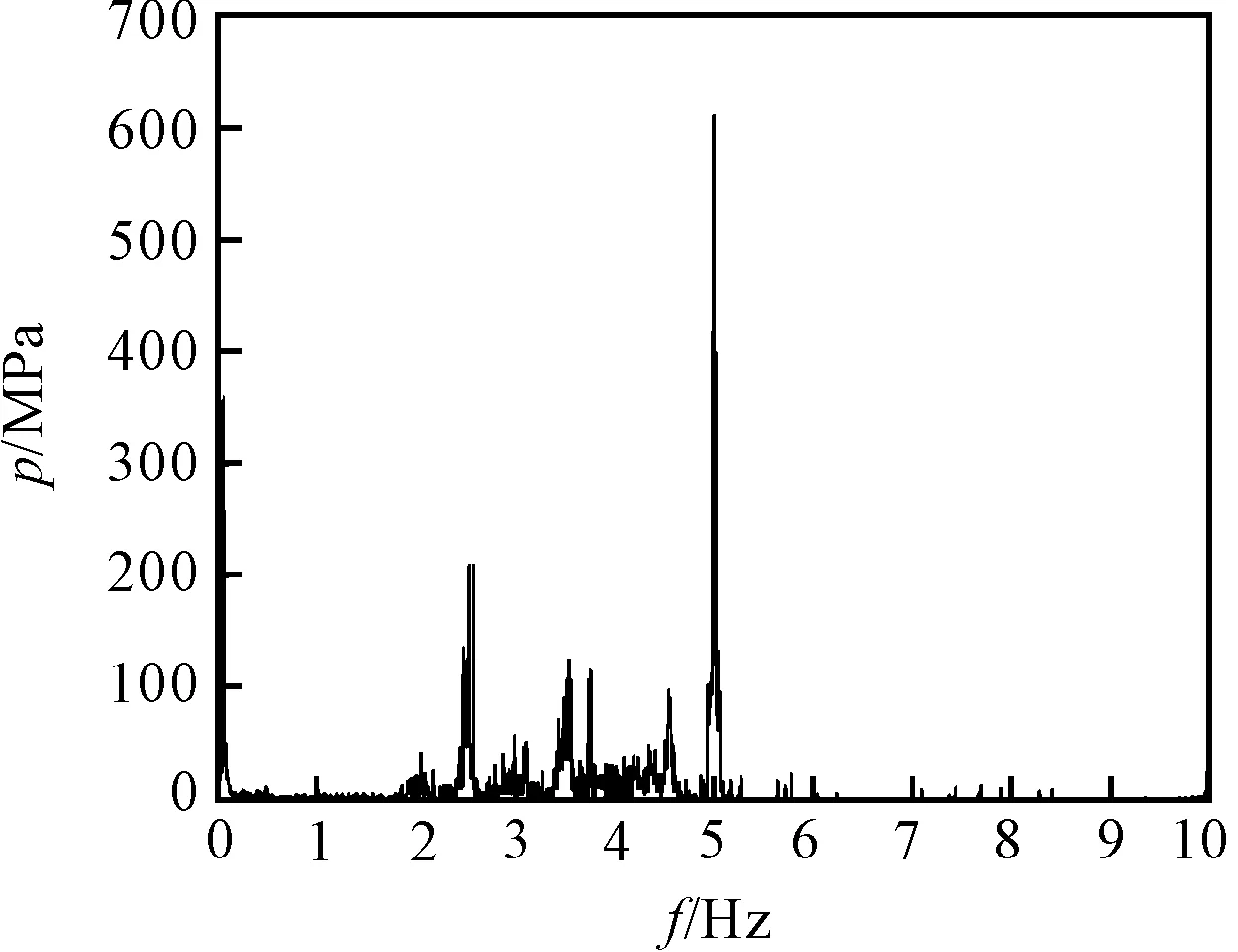
图8 检测点2 HHT变换边际谱

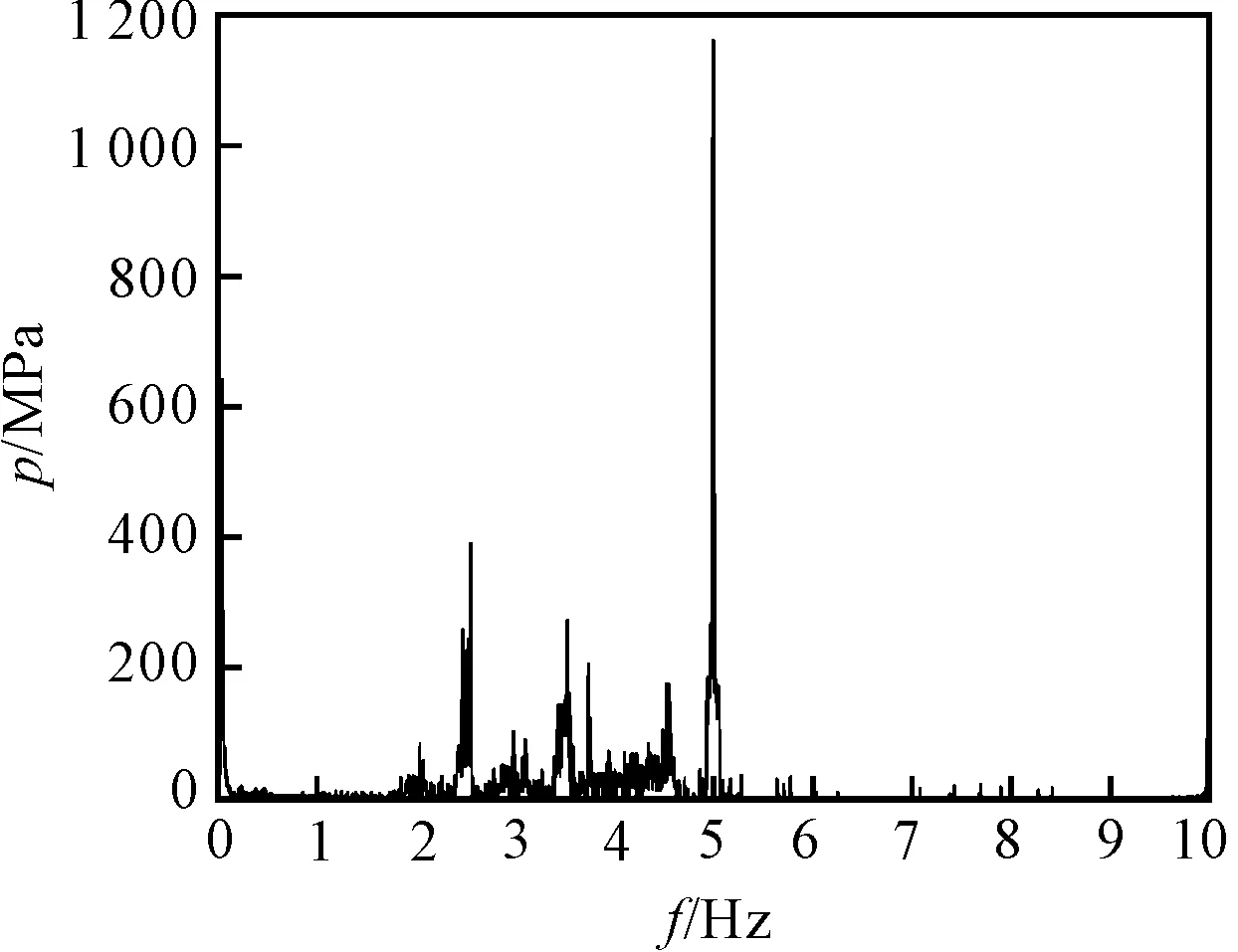
图9 检测点3 HHT变换边际谱

图(7～9)中的边际谱反应了压力脉动时域信号中含有的频率和幅值情况，可以看出有20 kHz、25 kHz、30 kHz、35 kHz、40 kHz、45 kHz、50 kHz等频率成分，同时幅度从监测点1到监测点3逐渐增大，这些信息与构建的入口速度函数的频率成分和幅度变化基本吻合，说明压力脉动的边际谱可以表征流道入口的速度频率变化和幅度变化情况。

湍动能是表征流道湍流性能的重要参数，因此，本研究在数值模拟过程中，记录了压力监测点所在平面上的湍动能动态变化过程。不同时刻的湍动能强度分布图如图10所示。

图10 不同时刻湍动能分布图

图10湍动能所处的时刻分别是入口函数速度频率为20 kHz、30 kHz、40 kHz、50 kHz、25 kHz、35 kHz、45 kHz所处的阶段的某一时刻。观察比较发现流道内的湍动能先不断增强，然后再慢慢减弱，这个变化跟入口速度的频率和幅度变化趋势是吻合的，而流道内的压力脉动频谱反映了入口速度的频率和幅度的变化，因此，压力脉动频谱可以反映出流道内的湍动能的变化情况。

4 实验与结果分析

4.1 压力脉动测控实验平台

针对本文所提出的基于HHT的约束流道压力脉动监测方法，笔者结合嵌入式控制技术，搭建了面向软性磨粒流加工在线调控的压力脉动测控实验平台，如图11所示。

图11 压力脉动测控实验平台

该平台采用嵌入式上下位机体系结构。上位机为基于嵌入式RISC处理器(ARM)的约束流道监测与控制系统，下位机为基于嵌入式数字信号处理器(DSP)的实时数据采集系统。下位机主要负责完成约束流道的脉动信号(压力/振动)、流量-流速信号、温度信号及其他磨粒流加工过程参数的实时采集，进行数字滤波处理后，按照既定数据传输协议对上述数据进行封装，通过串行通用接口上传至上位机。上位机接受下位机上传的实时数分组，根据数据传输协议进行解析，得到监测目标物理信号，通过人机交互接口在液晶显示屏显示，并根据用户的相关控制需求向磨粒流加工实验平台下达控制指令。

4.2 压力脉动实验结果与讨论

基于压力脉动测控平台可以得到当前流场的动压力，进而可换算出当前的流道入口速度，结合当前的流道温度，采用模糊控制方法就可以实现最优入口速度的在线调控，在线速度控制曲线如图12所示。

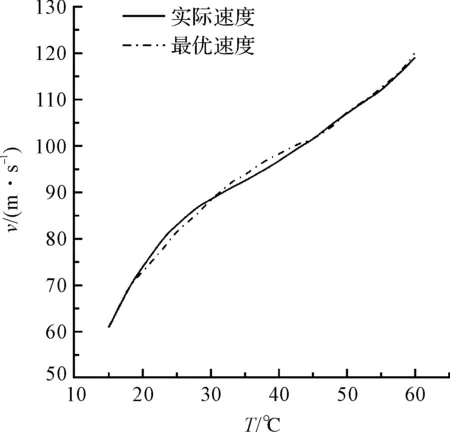
图12 在线速度控制曲线

基于上述磨粒流在线调控加工方法，以超声耦合强化加工方法为对象，对工件中段进行了加工对比实验，结果如图13所示。

图13 在线调控加工结果对比

通过图12、图13中结果可以说明上述调控方法可以很好地追踪最优速度，使得约束流道内流场在不断温升条件下得到连续、稳定、均匀的湍动能分布，进而有效提高表面质量。

5 结束语

本文对软性磨粒流抛光流道压力脉动进行了数值模拟和测控实验，采用HHT变换对压力脉动信号进行了频域上的分析研究，主要结论如下：

(1)针对软性磨粒流流道内的非线性非平稳的复杂流动状态，HHT变换是一种比较好的分析方式和手段；

(2)流道内的压力脉动信号经过HHT变换后得到的频谱信息，充分体现了流道入口磨粒流速度的频率和幅度等信息，也反映了流道内湍动能的变化状态，同时通过监测压力脉动信号实现了湍流调控。

因此，利用HHT变换方法分析软性磨粒流抛光流道内的压力脉动信息，可为今后软性磨粒流加工实现定向可控抛光，提高软性磨粒流加工的效率，避免出现“死角”弊端打下基础。

参考文献(References):

[1] 高 航,吴鸣宇,付有志,等.流体磨料光整加工理论与技术的发展[J].机械工程学报,2015,51(7):174-187.

[2] 袁巨龙,张飞虎,戴一帆,等.超精密加工领域科学技术发展研究[J].机械工程学报,2010,46(15):161-177.

[3] JI Shi-ming, XIAO Feng-qing, TAN Da-peng. Analytical method for softness abrasive flow field based on discrete phase model [J].ScienceChina,2010,53(10):2867-2877.

[4] 孙树峰,计时鸣,谭大鹏.低黏度液-固两相磨粒流湍流调控与结构化表面光整加工技术研究[J].中国机械工程,2011,22(19):2349-2353.

[5] 计时鸣,唐 波,谭大鹏.基于VOF的模具结构化表面软性磨粒流数值模拟[J].中国机械工程,2011,22(3):334-339.

[6] 计时鸣，池永为，谭大鹏,等.多种约束流道环境下的软性磨粒流流场特性[J].农业工程学报,2011,27(11):71-77.

[7] 计时鸣,周龙兵,谭大鹏.软性磨粒流精密加工工艺参数优化方法[J].中国机械工程,2013,22(3):334-339.

[8] 袁巧玲,计时鸣,文东辉,等.基于改进的低雷诺数湍流模型的软性磨粒流加工仿真与实验[J].中国机械工程,2014,25(6):800-807.

[9] 计时鸣,李 军,谭大鹏.基于超声波激振强化的软性磨粒流光整加工模拟与试验研究[J].机械工程学报,2016，52(21)：182-189.

[10] 赵 凯,仲兆平,王肖祎,等.基于HHT法的流化床生物质和石英砂双组分颗粒压差脉动信号分析[J].化工学报,2015,66(4):1282-1289.

[11] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[J].ProceedingsofRoyalSocietyofLondon,SeriesA,1998,454(1971):903-995.

[12] 张德胜,耿琳琳,施卫东,等.轴流泵水力模型压力脉动和振动特性试验[J].农业机械学报,2015,46(6):66-72.

[13] 俞 健，秦子明，方 超，等.旋涡泵压力脉动特性的研究[J].流体机械，2017(10)：31-36，63.

[14] 师艳平，张 一，权 龙，等.并联型双吸、排烟口轴向柱塞泵应用仿真研究[J].液压气动的密封，2016(6)：33-37.

[15] MAJIDI K. Numerical study of unsteady flow in a centrifugal pump[J].JournalofTurbomachinery，2005,127(2):363-371.