带隔板矩形贮箱俯仰晃动研究
应 磊, 周 叮, 房忠洁
(1. 南京工业大学 土木工程学院,南京 211816;2. 扬州工业职业技术学院,江苏 扬州 225000)
在工程实际中,贮液与贮液结构之间的耦合振动是非常重要的一个问题。对于上述问题,常采用有限元、边界元等数值方法进行求解,当边界规则时,可通过解析方法[1]求解。尹立中[2]、高索文等[3]运用两种不同的Lagrange函数,建立了液固耦合系统的耦合动力学方程,分别研究了矩形贮箱在水平与俯仰运动下的动力特性与响应。杜永峰等[4]基于剪切悬臂梁理论,对钢筋混凝土矩形贮液结构的自振频率与振型进行了研究,发现液动压力对频率影响不可忽略,对振型影响不大。程选生等[5]研究了带弹性隔板的双向壁式钢筋混凝土矩形贮液结构的振动特性,给出了液动压力计算的简化公式。
贮液的对流晃动常常会引起贮液结构的破坏,为抑制液体晃动,隔板是工程中常用的防晃措施。因此有必要对带隔板贮箱的晃动问题进行详细分析。王佳栋等[6-7]通过流体子域法,对带隔板圆柱形贮液结构的自振特性与动力响应做了系统研究。房忠洁等[8]对带隔板矩形贮液结构的自振特性做了相应的研究。
本文假设流体为无黏、无旋、不可压缩的理想流体、小震作用下液面做线性微幅晃动、贮箱与隔板均为刚性的,首先建立了水平激励下的带隔板矩形贮液结构的动力响应方程,通过液动剪力与液动弯矩相等,建立水平激励下的等效力学模型,并通过该等效力学模型研究了俯仰运动下的贮液晃动响应。
1 基本方程
1.1 流体控制方程
在水平地震作用下,只需考虑结构沿纵向或横向运动的情形, 因此可将矩形贮液结构在地震作用下的反应问题简化为平面问题而近似地求解,故将贮箱与流体之间的相互作用简化成图1所示模型。贮箱底部宽度为B,贮箱内充液高度为H,隔板长度为a,隔板所处高度为h。贮液密度为ρf。由于隔板厚度h远小于其他尺寸,可忽略不计,按图2将流体区域划分成4个子域Ωi(i=1,2,3,4),各个子域内流体的速度势为φi(x,z,t)。根据流体动力学理论,流体运动的速度势函数满足Lapalce方程:
(1)
Ωi中任意一点的速度:
(2)
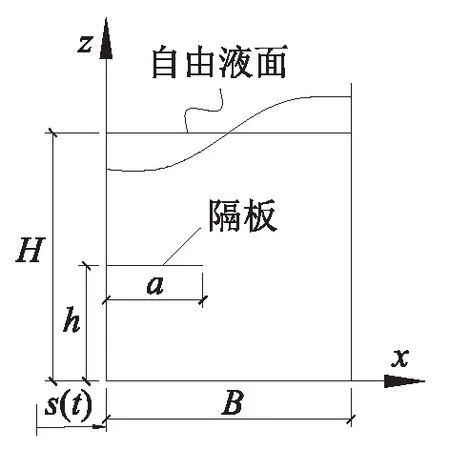
图1 贮箱及隔板 Fig.1 Tank and baffle
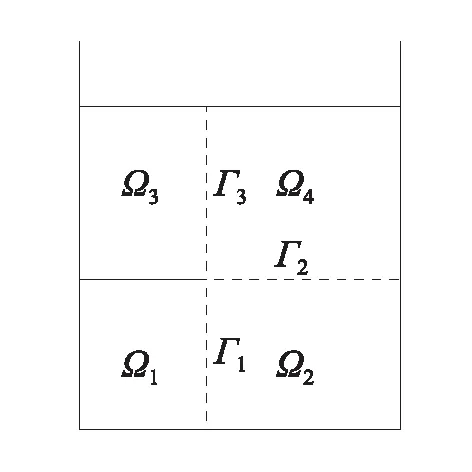
图2 液体子域及界面 Fig.2 Sub-domains and interfaces
1.2 边界条件

(3)
(4)
(5)
式中:fi(x,t)为自由液面晃动的波高方程且满足:
(6)
1.3 流体子域间界面方程
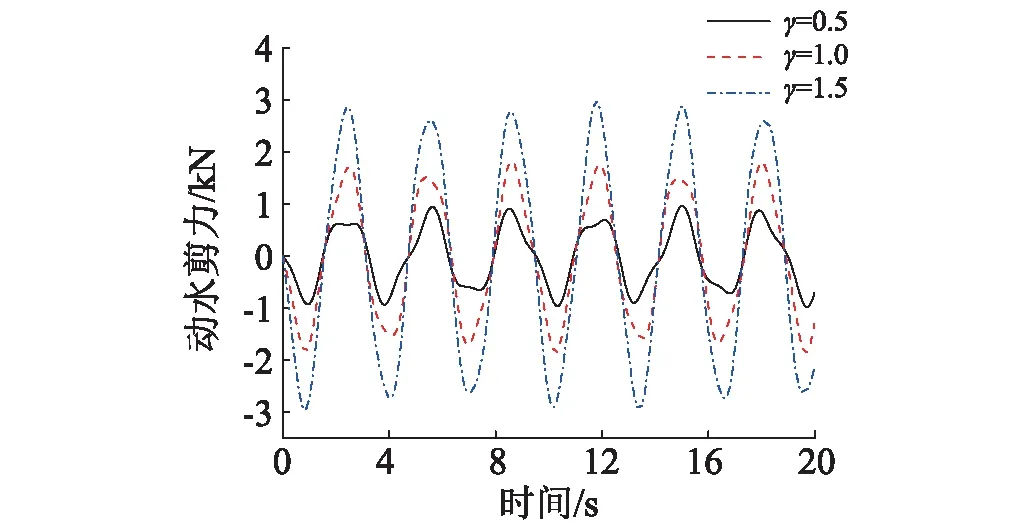
设P为流体子域内的任意一点,Ωi1和Ωi2(i1 φi1|P∈Γk=φi2|P∈Γk (7) 设n为不同子域交界面的法向量,则Ωi1和Ωi2在交界面Γk处的速度连续条件为: (8) 将速度势函数拆分成脉冲速度势φA和对流速度势φB两部分和: (9) φA(x,z,t)和φB(x,z,t)分别满足如下方程 2φA=0,2φB=0 (10) (11) (12) (13) (14) (15) 设Φ为流体自由晃动的振型函数,Φi为各个子域对应的振型函数。由文献[8]可得: 2Φi=0 (16) (17) (18) (19) 由式(16)~(19)可以看出,Φi的控制方程为二阶线性偏微分方程,其边界条件均为线性边界条件。显而易见,可采用叠加原理来求解Φi。设Φi为: (20) (21) 利用分离变量法便可求得各个子域内流体速度势的各分量,并将之代入式(18)~(19)即得含待定系数的级数方程,将所有级数截断至第N项,通过积分消元消除空间坐标得到特征方程,使用Matlab编程求解得到第n阶(n=1,2,…,N)晃动模态Φn与频率ωn。 设水平激励作用下的对流速度势为: (22) 将φA和φB代入式(14)与式(15)得: (23) 两边同乘Φn(x,H)并对x在0到B上进行积分,可得动力响应方程: (24) 式中: (25) 在建立动力响应方程时,由于忽略了隔板与流体的阻尼特性,实际高估了贮液的晃动响应,因此计算结果是偏于安全的。 根据伯努利方程,液体晃动产生的液动压力为: (26) 沿侧壁积分,得到水平动水剪力(水平向右)为: (27) 分别对侧壁、底部及隔板进行积分,得到对底部中心的动水弯矩响应(顺时针)为: (28) (29) (30) 式中: (31) (32) (33) (34) 将式(27)~(30)截断至第N项,有: (35a) (35b) (35c) (35d) 对式(24),两边同时乘以Tn/Mn得: (36) 对式(35a)变换得: (37) 结合式(36)和式(37)可知,流体的每一阶晃动分量皆可拆分成相应的对流分量与脉冲分量,而每一阶对流分量与脉冲分量的等效质量可由剪力相等条件确定: 第n阶晃动分量中对流分量等效质量: Tn,n=1,2,…,N 第n阶晃动分量中脉冲分量等效质量: 对式(35b)~ (35d)作类似变换可得: (38) (39) (40) 由第n阶晃动分量产生的动水弯矩可以确立对应阶对流与脉冲质量的等效高度,则:对侧壁作用弯矩提供的第n阶晃动分量中对流与脉冲分量的等效高度分别为: (41) 对底部作用弯矩提供的第n阶晃动分量中对流与脉冲分量的等效高度分别为: (42) 对隔板作用弯矩提高的第n阶晃动分量中对流与脉冲分量的等效高度分别为: (43) 综合考虑侧壁、底部、隔板的动水弯矩,第n阶晃动分量中对流分量与脉冲分量的等效高度Hn与H0n分别为: (44) 如图3(a),对于水平激励下的连续流体的动力响应求解,可等效为N组等效力学模型的响应和问题。将等效地震激励转换成等效荷载激励,得到图3(b)所示的静止地基上的等效荷载激励力学模型。等效荷载满足: (45) 图3 等效力学模型 Fig.3 Equivalent mechanical model 假设贮箱绕底部中心做俯仰运动,根据等效力学模型,考虑水平俯仰耦合运动,对流等效质量的运动控制方程为: (46) 图4 耦合晃动模型 Fig.4 Coupling sloshing model 前N阶晃动分量贡献的液动剪力与弯矩分别为: (47) (48) A1=1,A2=0时,系统受水平激励。图5分别给出了x=1/3、2/3处的液面波高时程曲线的本文解与有限元软件ADINA计算结果之间的时程对比曲线,由图可知,两者吻合良好。当x=1/3时,两者的峰值分别为0.030 6 m与0.030 0 m,峰值相对误差为1.71%。当x=2/3时,两者的峰值分别为0.030 8 m与0.030 0 m,峰值相对误差为2.36%。从而验证了本文建立的带隔板贮箱在水平激励下的动力响应相关理论的正确。 图5 x=1/3、2/3处的液面波高时程曲线 Fig.5 Time history of height of wave at x=1/3、2/3 图6分别给出了在不同激励频率ω=2和ω=5下,由等效力学模型与有限元软件ADINA求解得到的水平动水剪力时程对比曲线。当ω=2时,ADINA解与本文解的峰值分别为1143.6 N和1 130.4 N,两者峰值相对误差为1.15%。当ω=5时,ADINA解与本文解的峰值分别为4 264.9 N和4 317.1 N,两者峰值相对误差为1.22%。由图6可知,两者整体吻合良好,从而验证了水平激励下等效力学模型的正确性。 图6 ω=2、5时动水剪力时程曲线 Fig.6 Time history of hydrodynamic shear when ω=2, 5 图7 俯仰激励下动水剪力时程曲线 Fig.7 Time history of hydrodynamic shear under pitching loads A1=0,A2=1时,系统受俯仰激励。文献[9]采用Housner模型[10]在SSI问题中研究了矩形储液结构在水平与摇摆耦合运动下的动力响应,图7给出了H=0.5,a=0.1,h=0.1时,本文等效力学模型同Housner模型在不同频率(ω=30、2)的俯仰激励下的水平动水剪力对比时程曲线。当隔板较短时,有隔板与无隔板两者动力响应应该一致。由图可知,两者虽有出入,但大体走势一致,吻合良好,从而验证了用等效力学模型近似考虑平仰耦合运动的合理性。 取A1=A2=1,同时考虑渡槽的水平运动与俯仰运动。定义俯仰因子β=[max(ShearP)-max(ShearL)]/ max(ShearL)。 图8(a)给出了ω=2时,不同储液高宽比(γ=H/B=0.5、1、1.5)下的平仰耦合动水剪力时程曲线,其俯仰因子β分别为0.536 2、0.618 9、0.810 4。图8(b)给出了不同高宽下的平仰耦合相对于各自的仅平动下的动水剪力的对比时程曲线。由图8可知,相对矮胖的储液结构受俯仰晃动影响较小,相对高瘦的储液结构则受俯仰晃动影响明显。 (a) (b)图8 不同H/B下的动水剪力时程曲线 Fig.8 Time history of hydrodynamic shear under different H/B 图9 隔板长度及高度对俯仰因子β的影响 Fig.9 Influence of length and height of baffle on β 图9(a)和图9(b)给出了在ω=2时,不同隔板长度a/B与高度h/H对β的影响。隔板高度一定时,隔板越长,β越大。隔板长度一定时,隔板所处位置越高,β越大。且当隔板较长或所处位置较高时,增高或增长隔板对β加剧最为明显。 本文建立带隔板矩形截面渡槽在水平激励下的运动方程,然后构造等效力学模型,通过等效力学模型考虑水平与俯仰耦合运动的动力响应,对隔板长度与高度、充液高宽比等参数进行参数分析,得到如下结论。 (1) 高宽比较大时,考虑平仰耦合相对于纯平动下的动力响应放大明显,应予以考虑,相对矮胖的结构,平仰耦合对动力响应影响较小,可按平动考虑。 (2) 隔板越长,所处位置越高,平仰耦合动力响应峰值越大,俯仰运动动力响应峰值越大。 [ 1 ] 苟兴宇, 王本利, 马兴瑞, 等. 液固纵向耦合系统的受迫响应[J]. 振动工程学报, 1998, 11(2): 31-37. GOU Xingyu, WANG Benli, MA Xingrui, et al. Forced response of vertical liquid-solid coupling system [J]. Journal of Vibration Engineering, 1998, 11(2): 31-37. [ 2 ] 尹立中, 刘敏, 王本利, 等. 矩形贮箱类液固耦合系统的平动响应研究[J]. 振动工程学报, 2000, 13(3): 113- 117. YIN Lizhong, LIU Min, WANG Benli, et al. Study on dynamic response of the liquid-solid coupling system with the liquid in a rectangular container under horizontal excitation [J]. Journal of Vibration Engineering, 2000, 13(3): 113-117. [ 3 ] 高索文, 尹立中, 王本利, 等. 矩形贮箱类液固耦合系统转动特性分析[J]. 振动与冲击, 2000,19(3): 19-21. GAO Suowen, YIN Lizhong, WANG Benli, et al. Analysis on dynamic characteristics of the liquid-solid coupling system with liquid in a rectangular container under pitching excitation [J]. Journal of Vibration and Shock, 2000, 19(3): 19- 21. [ 4 ] 杜永峰, 史晓宇, 程选生. 钢筋混凝土矩形贮液结构的液固耦合振动[J]. 甘肃科学学报, 2008, 20(2): 45-49. DU Yongfeng, SHI Xiaoyu, CHENG Xuansheng. Vibration of reinforced concrete rectangular liquid-storage structures with liquid-structure interaction [J]. Journal of Gansu Sciences, 2008, 20(2): 45-49. [ 5 ] 程选生, 杜永峰. 弹性壁板下钢筋混凝土矩形贮液结构的液动压力[J]. 工程力学, 2009, 26(6): 82-88. CHENG Xuansheng, DU Yongfeng. The dynamic fluid pressure of reinforced concrete rectangular liquid-storage tanks with elastic walls [J]. Engineering Mechanics, 2009, 26(6): 82-88. [ 6 ] 王佳栋, 周叮, 刘伟庆. 带环形隔板圆柱形储液罐中液体晃动的解析研究[J]. 振动与冲击, 2010, 29(2): 54-59. WANG Jiadong, ZHOU Ding, LIU Weiqing. Analytical solution for liquid sloshing with small amplitude in a cylindrical tank with an annual baffle [J]. Journal of Vibration and Shock, 2010, 29(2): 54-59. [ 7 ] 王佳栋, 周叮, 刘伟庆. 水平激励下带环形刚性隔板圆柱形储液罐中流体的晃动响应[J]. 力学季刊, 2011,32(2): 166-172. WANG Jiadong, ZHOU Ding, LIU Weiqing. Sloshing response of liquid in cylindrical tank with a rigid baffle under horizontal loads [J]. Chinese Quarterly of Mechanics, 2011, 32(2): 166-172. [ 8 ] 房忠洁, 周叮, 王佳栋, 等. 带隔板的矩形截面渡槽内液体的晃动特性[J]. 振动与冲击, 2016, 35(3): 169-175. FANG Zhongjie, ZHOU Ding, WANG Jiadong, et al. Sloshing characteristics of liquid in a rectangular adequate with baffle [J]. Journal of Vibration and Shock , 2016, 35(3): 169-175. [ 9 ] LIVAOGLU R. Investigation of seismic behavior of fluid-rectangular tank-soil/ foundation systems in frequency domain [J]. Soil Dynamics and Earthquake Engineering, 2008, 28: 132-146. [10] HOUSNER G W. Dynamic pressures on accelerated fluid containers [J]. Bulletin of Seismological Society of America, 1957, 47(1): 15-35.2 水平运动方程的建立
2.1 速度势函数的分解

2.2 子域法求解自由晃动模态

2.3 动力响应方程的建立与求解
3 等效力学模型的建立
3.1 等效力学模型




3.2 水平俯仰耦合晃动

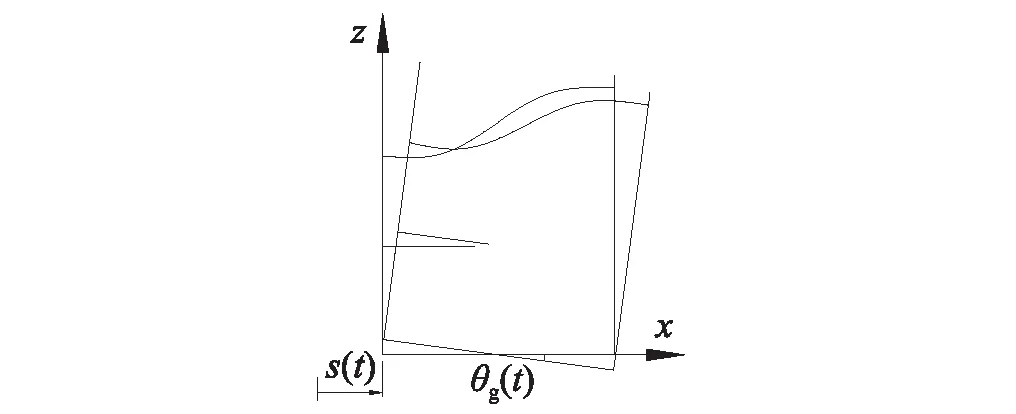
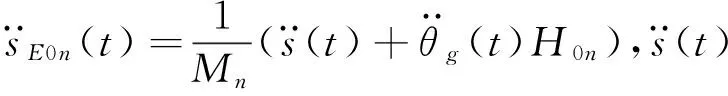
4 模型验证
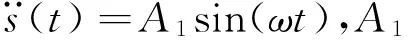



5 参数分析



6 结 论

