三维磁特性测试系统中激磁与传感结构的校准与补偿

耿 鑫， 李永建， 王利祥

(电磁场与电器可靠性省部共建重点实验室， 河北工业大学， 天津 300130)

1 引言

随着科学技术的发展，电工磁性材料磁特性的精确模拟日益重要，这关系到电工设备的节能降耗，是当今计算电磁学的热点问题之一[1]。

磁场分析中，国际电工委员会(IEC)将爱泼斯坦方圈法、环形样件法定为标准，其均为一维磁特性测量，假定B和H平行，忽略介质的各向异性，这无疑降低了实验精度。日本已经研发出正交双向激励二维单片磁特性测量装置，并对H传感线圈进行了定标研究，该装置能较好地反应硅钢片的各向异性[2-4]。但在实际工况中，如旋转电机、三相变压器“T”型接合部分，即使在一维交变场或二维旋转场下，因为旋转磁畴和畴壁移动而呈现三维磁特性，B、H矢量的轨迹呈现空间分布，非常复杂，并且磁滞特性和磁心损耗的计算都与实测的B、H传感信号有关[5-8]。因此，适用于三维空间的B-H传感线圈的研究显得至关重要。

本文提出了一种新型的线圈结构，并针对线圈进行了一系列的校准实验，深入分析了直流激磁和交流激磁模型的不同，根据旋转坐标变化的原理对激磁与传感轴进行了补偿研究。

2 B-H传感线圈

新型B-H复合传感线圈与传感箱结构如图1所示[9]。图1(a)中，表面贴装的H线圈采用线径0.05mm的漆包线紧密均匀地缠绕在0.40mm厚的环氧树脂基板上，每层100匝，共2层，采用上下两层往返交叉绕制并且进线和出线端双绞的方式，有效消除了线间谐波干扰，提高了测量精度；将小而薄的圆环形B线圈放在H线圈基板的中心孔中，环内径4.64mm，外径5.49mm，厚0.40mm，共60匝。

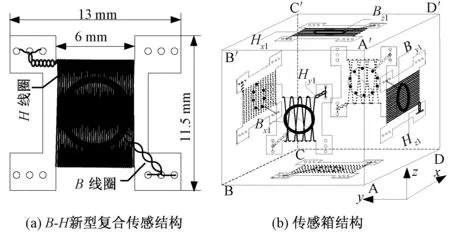
图1 新型传感线圈与传感箱结构图Fig.1 Structure of novel B-H sensing coil and sensing box

立方体传感箱是由6组B-H传感线圈按照给定的方向构成的，x、y、z三个方向要和激磁结构定义的方向严格一致，才能保证三维磁特性实验的正确实施，因为共用同一个基板的H和B线圈的窗口方向相互垂直，如x方向为Hy线圈和Bx线圈共用同一基板，同理y方向的传感线圈为Hz和By，z方向为Hx和Bz，如图1(b)所示。将边长为22mm的立方体样品置于传感箱中心，三对缩小的B-H线圈紧贴于样品表面的中心，线圈外面还设有相同材料的样品保护层，样品、线圈、保护层形成了“三明治”式结构，如图2(a)所示，相当于把传感线圈放置于样品内部测量，有效提高了测量精度。

图2 样品中的传感线圈示意图Fig.2 Sensing coil in sample

3 传感线圈的校准原理

磁场传感线圈如图2(b)所示。对每个传感线圈来说，即便只给一个方向(x)加激励，线圈不仅会在x方向产生感应电动势，在y、z方向也能感测到微弱的电压信号，因为线圈在y、z方向仍会有一定的磁感应“窗口面积”。虽然x方向的信号比y、z方向大几十倍，但对于三维磁特性的精确研究是不能忽略的，所以x、y、z三轴方向并非相对独立，而是相互影响。考虑到在空间各个方向的相互影响，线圈系数KH和KB的三维张量矩阵形式为：

对于矩阵的主对角元素校准，线圈施加激励时，因为B、H线圈“窗口面积”小且不易确定，所以线圈匝数与窗口面积的乘积不能准确得出，但系数的准确值是影响测量B、H非常关键的因素，为此，设计一个长螺线管，使其通入的正弦交流电为：

(1)

式中，I为激磁电流；f为激磁频率。

通电后，在螺线管中心区域产生均匀变化的磁场，将线圈置于长螺线管产生的均匀磁场中，根据法拉第电磁感应定律，线圈在均匀磁场的感应电动势为：

(2)

Ui=-2πfK0Bmcos(2πft)i=H,B

(3)

式中，U为线圈感应电动势；B为磁感应强度；K0为线圈匝数与面积之积；Bm为螺线管中心处磁感应强度最大值。由此可得：

(4)

Uimax由实验测出，即可得出主对角元素校准系数。

通入直流电的长螺线管会在螺线管中心产生均匀的恒定磁场，将被测线圈置于螺线管中心的瞬间，线圈会有磁通穿过，通过控制电源的开断，测量穿过线圈的磁通与磁感应强度的比值，可得到线圈的窗口面积与匝数的乘积：

(5)

式中，Φ0为穿过测量线圈的磁通量；B0为通电螺线管中心处磁感应强度。

对于三维张量的非主对角元素校准，如图2(b)中Hx线圈，非主对角线系数KHxy、KHxz分别表示Hx线圈在y、z方向的线圈系数。由于线圈薄且绕线间有间隙，Hx线圈同z方向垂直的线圈表面积大于同y方向垂直的表面积，即KHxx>>KHxz>>KHxy。如果线圈绕置细密，薄基板边缘光滑，KHxy可被忽略。对于KHxz可根据在Hx线圈中的薄圆环形Bz线圈所测得的感应电动势信号进行校准。对于其他两方向的校准也需借助相应的内嵌B线圈来实现。

4 螺线管磁场仿真分析

为进一步提高三维磁特性的实验精度，进行模型仿真实验，设计螺线管模型长1000mm，内半径70.80mm，外半径74.80mm，采用双层绕制，共1080匝，如图3所示。通入式(1)的激磁电流时，由仿真得出沿螺线管轴向的磁通密度如图4所示。

图3 长螺线管结构示意图Fig.3 Structure of long solenoid

图4 螺线管磁通密度云图Fig.4 Cloud map of magnetic flux density inside solenoid

仿真得出螺线管中心处B0=5.76×10-3T，由图4可知，螺线管产生的磁场相对较均匀。根据式(6)得出螺线管正中心区域的不均匀度为0.00390114。

(6)

式中，β为螺线管磁场的不均匀度；B0、B1分别为该螺线管磁通密度最大值、最小值。

对该模型进行理论分析，根据式(7)计算：

(7)

式中，N为螺线管每层单位长度的匝数；N1为螺线管单位厚度上的层数；r0、r分别为螺线管的内、外半径；I为线圈通入的激磁电流；L为螺线管长度。

考虑到实验系统的电源为220V的市电，并不是我们理想的220V的正弦交流电，在经过调压器降压时可能有微小的谐波振动，产生干扰信号，所以分别采用直流激磁和交流激磁以及仿真，给长螺线管通入相同的4A电流，采集到长螺线管内不同位置的磁通密度，如图5所示。

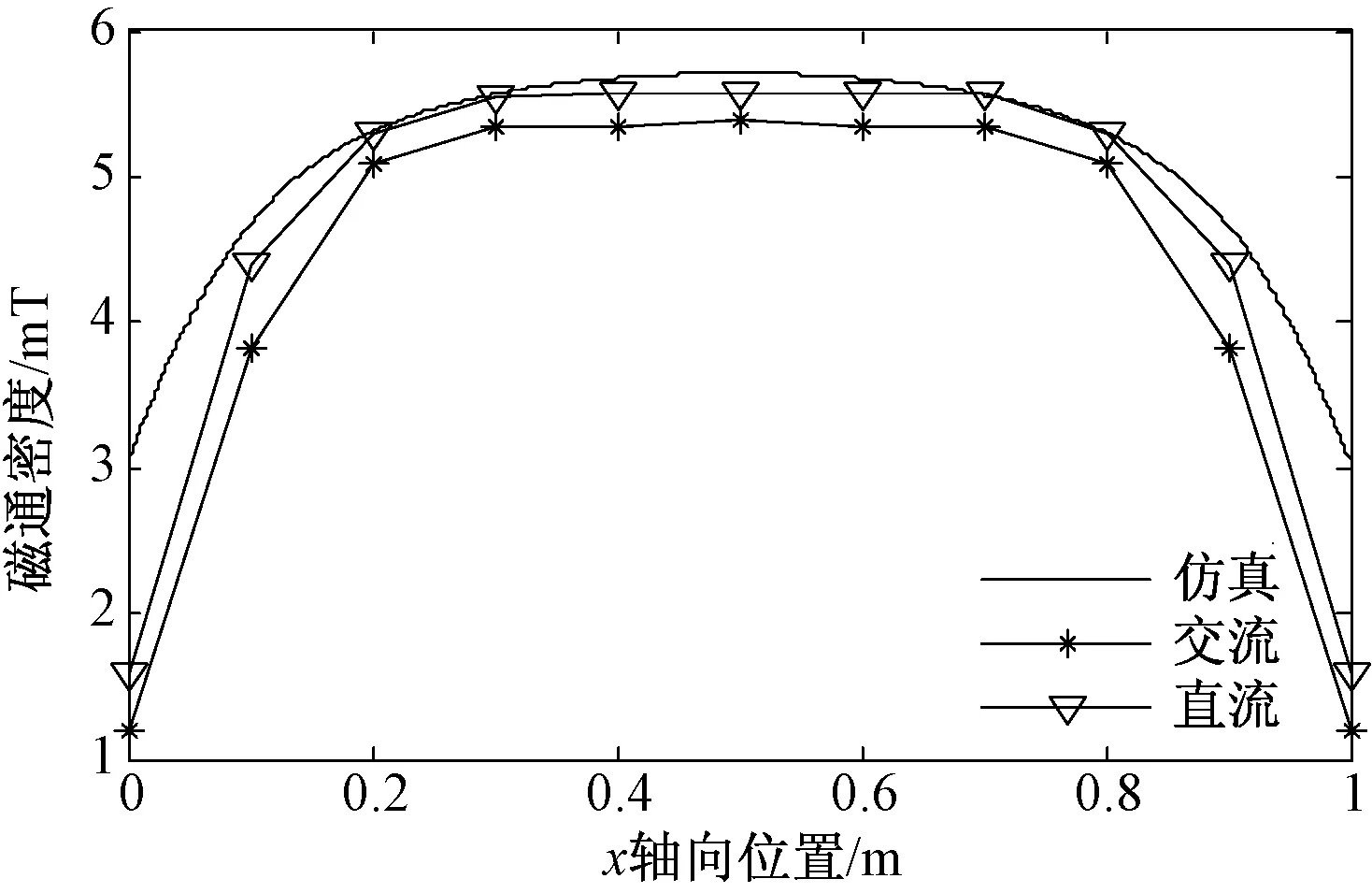
图5 沿x轴向的磁通密度分布Fig.5 Magnetic flux density distribution along x-axis

可以看出，3种方法在螺线管中的磁通密度基本保持一致，直流激磁模型相对较大一些，均是越靠近螺线管边缘，磁场越弱，越靠近其中心，磁场越强，在中心位置均匀性很好。

由此得出各个模型在螺线管中心处的磁通密度以及与理论值的误差，结果如表1所示。

表1 各个模型的磁通密度值Tab.1 Flux density value of each model

选取一组B-H线圈，实验采用高斯计测量螺线管中心位置的磁场，交流系统测得的螺线管中心磁通密度Ba、直流系统下测量的恒定磁通密度Bd以及根据式(7)计算的激磁电流1～4.5A时磁通密度Bc相比较，结果如图6所示。可以看出，线圈的Bc、Ba、Bd值基本一致，Bd稍大一些，但线性度很好。

图6 传感线圈磁通密度计算值和实验值的比较Fig.6 Comparison between calculated and experimental values of magnetic flux density of sensing coil

从仿真、实验、理论计算三种方法对比了螺线管的内部磁场，完全满足实验要求，可以实现传感线圈主对角元素的精确校准，验证了螺线管磁场计算的可行性。

5 传感线圈系数的校准实验

5.1 直流系统实验设置

图7(a)为直流激磁系统流程，直流激磁系统包括：①直流稳压电源，提供直流电；②负载阻抗，匹配电路负载，调节通入螺线管电流的大小；③螺线管，通电后能感应出均匀的磁场，使传感线圈在均匀磁场中可以感应出电动势；④磁通计，用来测量给定直流电瞬间通入测量线圈的磁通变化。图7(b)为测量系统实物图。

图7 直流激磁测量图Fig.7 Chart of DC excitation measurement

5.2 交流系统实验设置

图8(a)为交流系统实验流程，交流激磁系统包括：①小型调压变压器，实现降压功能，调节50Hz的工频电压，控制通入螺线管电流的大小；②水冷电阻，将电阻放在水中，助于散热；③电流表，用来显示整个线路有效电流的大小；④差分放大电路，由于采集的传感线圈的感应电动势信号非常弱小，需要经过放大和滤波处理，得出平滑且无毛刺的感应信号波形；⑤示波器，将采集到的感应电动势信号通过示波器显示出来；⑥计算机，处理采集到的感应电动势信号，得出结果。图8(b)为测量系统实物图。

图8 交流激磁测量图Fig.8 Chart of AC excitation measurement

无论是交流激磁还是直流激磁，在校准实验中，都需要调整立方体的“窗口”保证与螺线管的轴向方向垂直，以此来获得最大磁通量。通过微调螺线管内固定传感箱的转动托盘来改变位置，在感应电动势和磁通量最大时进行实验校准，使测量结果更准确。

5.3 非主对角元素校准实验设置

对于三维张量的非主对角元素校准需要在三维磁特性装置装有待测样品的情况下进行。非主对角元素数值非常小而且与实验环境有密切关系，不宜用激磁功率很小的螺线管来校准。另外，非主对角线系数反映的是三维测试环境下磁场的相互关系，相当于在实际实验环境中进行的校准，三维磁特性测试系统中的三组高性能功率放大器能提供比较强的激磁磁场，而且被测样品的相对磁导率远大于真空磁导率，相当于放大了感应磁场，更利于信号的采集与计算。

5.4 实验结果及分析

采用直流系统通入的激磁电流为1～4.5A时，测得的三组B、H线圈通过的磁通量与电流的关系如图9所示。传感线圈的磁通量随电流增加基本呈线性增长，三组H线圈虽有差异但基本涨幅一致，说明线圈系数相差很小，但在电流达到2.5A时，各个线圈通过的磁通量已有了明显的区分，线圈Hy的系数最大。

图9 B、H线圈的磁通与电流的关系Fig.9 Relationship between flux and current of H and B coils

交流系统通入激磁电流的有效值1～7A时，将采集到的感应电动势信号经过放大电路放大200倍，再进行滤波，除去杂波干扰后，采集3组B-H传感线圈电动势的有效值，其与电流之间的关系如图10所示。随着电流的增加，线圈的感应电动势呈线性增长，说明各个线圈均匀度很好。

图10 传感线圈感应电动势有效值Fig.10 Effective value of EMF signals of sensing coil

50Hz下，三维磁特性装置中有待测样品，且只在x方向加给定激励，通过检测系统采集H、B线圈六个电压传感信号和x方向的电流采样信号，结果如图11所示。三组线圈的电压信号波形、相位大体一致，与电流波形相差90°，证明每个线圈感应信号方向与激磁结构规定方向一致，否则会出现相差180°的波形相位差。三组H线圈的电压信号的幅值大体一致，说明三组H线圈的一致性很好。

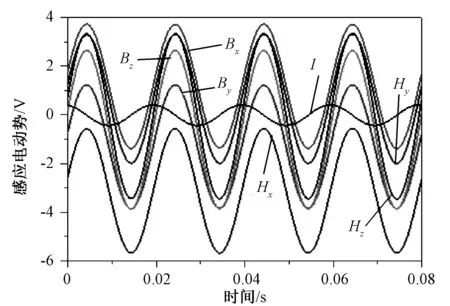
图11 传感线圈的感应电动势信号Fig.11 EMF signals of sensing coil

将采集到的信号经过复杂的数据处理，交流和直流激磁系统的线圈系数均取平均值，如表2所示。B、H线圈在直流系统测得的主对角线的校准系数较小一些，这是因为直流激磁时螺线管内磁场为直流激励产生的磁场与地磁场的叠加，这跟螺线管放置的位置有关，当螺线管产生磁场与地磁场方向完全一致时，影响最大。所以地球空间的电磁环境对外在磁场有一定的影响，不同位置地磁场的强度不同，影响也不同，所以应对当地地磁场进行测量校准，避免误差影响。

表2 线圈主对角线校准系数Tab.2 Principal diagonal calibration coefficient of sensing coils (单位：×10-3 m2)

由于线圈非主对角线系数值很小，改变激磁频率对其造成的影响会很大，在三维磁测量系统中进行非主对角元素校准， 5Hz、50Hz、100Hz、500Hz、1000Hz激磁频率下的H线圈和B线圈非对角线系数值如表3所示。

表3 不同激磁频率下H、B线圈非主对角元素系数Tab.3 Non principal diagonal elements of H and B coils under different excitation frequency (单位：×10-6 m2)

5.5 传感线圈的测量误差补偿

在非对角元素测量实验中，激磁结构与传感结构的坐标要完全一致，但在拆放立方体样品时，很难保证传感轴与激磁轴的重合，激磁与传感结构如图12(a)所示。这将严重影响实验的测量精度，所以采用旋转坐标变换消除由系统误差造成的偏差角。因为B信号为受控信号，所以只需对H信号进行补偿。

图12 激磁与传感坐标关系图Fig.12 Excitation sensor coordinate relation graph

在如图12(b)所示的坐标系中，x、y、z为三维测量系统中正交激磁坐标轴，x′、y′、z′为传感箱的偏差坐标轴。x′与x、y、z三轴之间的夹角分别定义为α1、β1和γ1，y′与x、y、z三轴之间的夹角分别定义为α2、β2和γ2，z′与x、y、z三轴之间的夹角分别定义为α3、β3和γ3。则磁场强度的转换公式为：

(8)

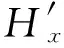
根据磁场强度实验值与测得的偏差角修正得出H的真实值，因为样品放置的人为性，偏差角会一直存在，所以每进行一次实验就要进行一次角度补偿，以保证三维磁特性测量的实验精度。

6 结论

本文针对新型B-H传感线圈，提出了线圈系数的张量模型，设计了可靠的长直螺线管和三套完整的校准实验装置。

提出了一种直流激磁模型，全面对比分析了直流和交流激磁模型的线圈系数校准值，证实了采用直流激磁系统时需要考虑外在地磁场的作用，并且不同的位置和不同方向受地磁场的影响也不相同,所以要对当地地磁场进行磁场补偿。

设计了激磁轴与传感轴偏差角补偿方案，可消除三维磁测量装置中激磁与传感结构坐标不一致造成的误差，为进一步提高三维磁特性测量精度提供了依据。

参考文献(References)：

[1] Sievert J. The measurement of magnetic properties of electrical sheet steel - Survey on methods and situation of standards[J]. Journal of Magnetism & Magnetic Materials, 2000, 215-216(3):647-651.

[2] Zhu J G, Ramsden V S. Improved formulations for rotational core losses in rotating electrical machines[J]. IEEE Transactions on Magnetics, 1998, 34(4):2234-2242.

[3] Li Y, Yang Q, Zhu J, et al. Design and analysis of a novel 3-D magnetization structure for laminated silicon steel[J]. IEEE Transactions on Magnetics, 2014, 50(2):389-392.

[4] 张艳丽, 何厚键, 谢德馨, 等 (Zhang Yanli, He Houjian, Xie Dexin, et al.) 基于二维磁特性测量的电工钢片矢量磁滞模型 (Vector magnetic hysteresis model of electrical steel sheets based on two-dimensional magnetic property measurement) [J]. 中国电机工程学报(Proceedings of the CESS), 2010, 30(3): 130-135.

[5] Zeng J, Guo Y, Li Y, et al. Two-dimensional magnetic property measurement for magneto-rheological elastomer[J]. Journal of Applied Physics, 2013, 113(17):17A919-17A919-3.

[6] Cullity B D, Garham C D. Introduction to magnetic materials [M]. New Jersey, USA: John Wiley & Sons, 2011.

[7] Dlala E. A simplified iron loss model for laminated magnetic cores[J]. IEEE Transactions on Magnetics, 2008, 44(11):3169-3172.

[8] Enokizono M, Fujiyama S, Simoji H, et al. Localized distribution of two-dimensional magnetic properties in three-phase induction motor core model[J]. Journal of Magnetism & Magnetic Materials, 2000, 215-216(1):772-775.

[9] 薛刚，李永建，曹磊，等 (Xue Gang， Li Yongjian， Cao Lei，et al.). 磁性材料三维磁特性传感信号检测技术中关键问题的研究与分析 (Research and analysis on several key issues of sensor signal detection of three-dimensional (3D) magnetic properties) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2016,35(5):19-22.