五桥臂逆变器最少模态SVPWM调制机理及特性

王文斌， 张 波

(华南理工大学电力学院， 广东 广州 510641)

1 引言

逆变器广泛应用于各种不间断电源、交流电机驱动及并网供电系统中。然而，随着大功率、多负载发展的需要，要求逆变器具有同时给两个或多个交流负载的供电能力，为此多负载逆变器成为一个新的研究方向。文献[1]提出了一种具有五个桥臂的双输出逆变器，该五桥臂逆变器在保证调制波幅值之和不大于载波幅值的情况下，能够实现两个负载的独立控制，从而解决了同时供给多个负载的问题。文献[2-5]研究五桥臂逆变器的空间矢量脉宽调制(SVPWM)与正弦脉宽调制(SPWM)策略，证明SVPWM策略具有更高的电压利用率，SVPWM成为五桥臂逆变器主流调制策略。然而，现有的五桥臂逆变器SVPWM使用所有的空间矢量来跟踪合成参考矢量，没有深入研究开关序列与系统状态切换的内在联系，未能从可控性的角度来设计开关序列，导致开关序列非常冗长，因此不能有效降低功率器件的开关频率。为了最小化工作模态的数量和简化系统中使用的开关序列，文献[6-10]对混杂系统可控性进行深入研究，文献[11]在此基础上进一步研究了多模态变换器的可控性，并提出了最少模态可控性，在理论上验证了减少系统工作模态的可行性。文献[12,13]初步尝试将最少模态可控性应用于电力变换器SVPWM调制策略的模态简化中，仅用一半数量的工作模态就可实现系统可控，简化后的系统开关序列较现有SVPWM技术更为简短，从而使得开关损耗降低。经过实际验证，最少模态可控性适用于几乎所有多模态混杂系统的分析研究，可实现多模态混杂系统控制的简化。

五桥臂逆变器也是一类具有多个工作模态的混杂系统，因此最少模态可控性理论适用于此类逆变器的分析。本文研究了五桥臂逆变器的工作模态，以此建立了五桥臂逆变器的切换线性系统模型，引入最少模态可控性理论研究了五桥臂逆变器的最少模态可控性，找出五桥臂逆变器最少模态可控方案，并设计了6个模态控制下五桥臂逆变器的开关序列，从而得到用于五桥臂逆变器的新型空间矢量脉宽调制策略。

2 五桥臂逆变器的切换线性系统模型

根据切换线性系统理论，任何具有k种工作模态的功率变换器均可表述为：

(1)

式中，x(t)为状态向量；u(t)为输入向量；y(t)为测量输出；σ(t)={1,2,…,k}，为对应于k种工作模态的开关序列；A、B、C为系统模型参数。

五桥臂逆变器拓扑如图1所示。该逆变器由5个桥臂构成，其中一个桥臂作为公共桥臂，由此可以供电给2个三相负载。S3、S8为公共桥臂，S1、S6桥臂和S2、S7桥臂与其构成逆变器a；S4、S9桥臂和S5、S10桥臂与其构成逆变器b。

图1 五桥臂逆变器拓扑Fig.1 Topology of five-leg inverter

五桥臂逆变器采用SVPWM控制时，其具体工作模态及其对应的空间矢量如表1 所示。当其中一个逆变器处于工作状态时，另一个逆变器剩余的两个桥臂都与公共桥臂处于同一工作状态，即零矢量状态，以此将未工作的逆变器闭锁，从而实现两个逆变器的独立控制。

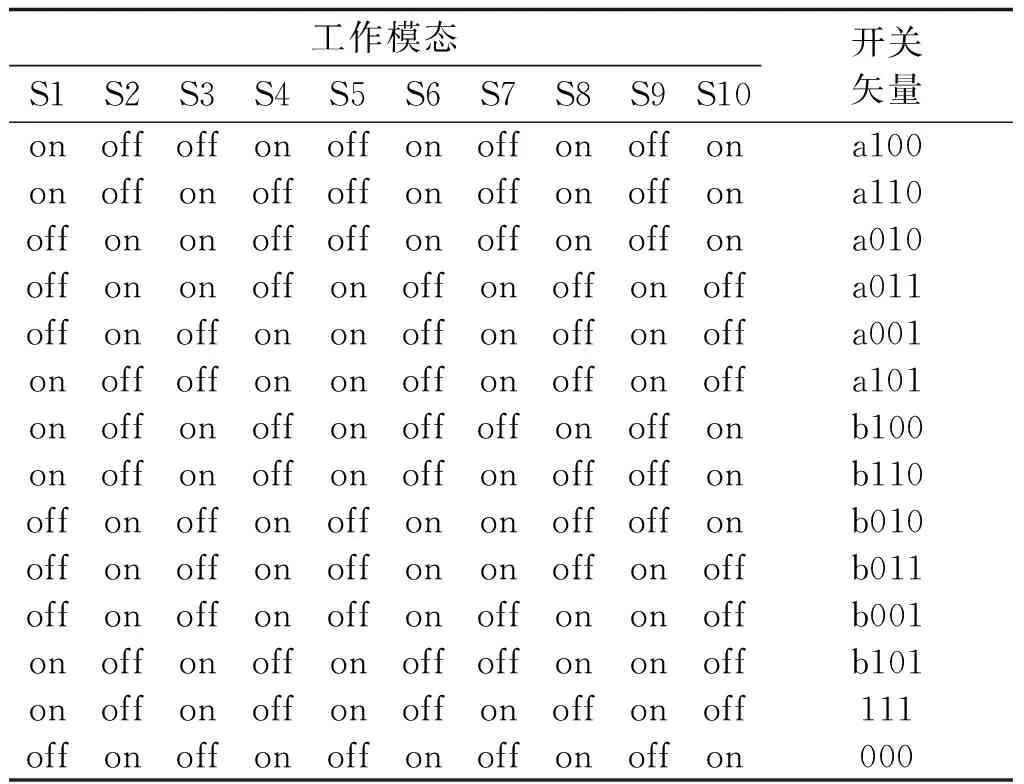
表1 SVPWM的工作模态和对应空间矢量[3]Tab.1 Operation modes and corresponding space vectors for SVPWM[3]

现有SVPWM策略使用14个矢量生成两路独立的三相输出电压。选择状态变量x=[x1x2]T,其中x1=x2=[iaibicuaubuc]T，iabc、uabc分别为电感Labc的电流和电容器Cabc的电压。 令Ca=Cb=Cc=C，La=Lb=Lc=L，Ra=Rb=Rc=R，由表1可见，SVPWM调制下，五桥臂逆变器的开关状态共有14种，即系统共由14个子系统组成，其对应的切换线性系统模型参数如式(2)～式(6)所示：

(2)

(3)

(4)

(5)

(6)

式中，A1～A14、B1～B14、C1～C14分别为在对应工作模态下的系统模型参数矩阵。

3 五桥臂逆变器可控性分析

五桥臂逆变器在不同的调制技术下所用到的工作模态不尽相同，如SPWM控制策略仅用到12个工作模态，而SVPWM控制策略则用到了14个工作模态。由此可见，五桥臂逆变器可由不同数量的开关模态组合进行调制。显然，系统正常工作时所使用的工作模态越少，其算法实现也将越简单，因此本文引入最少模态可控的定义来研究五桥臂逆变器的最少模态可控性。

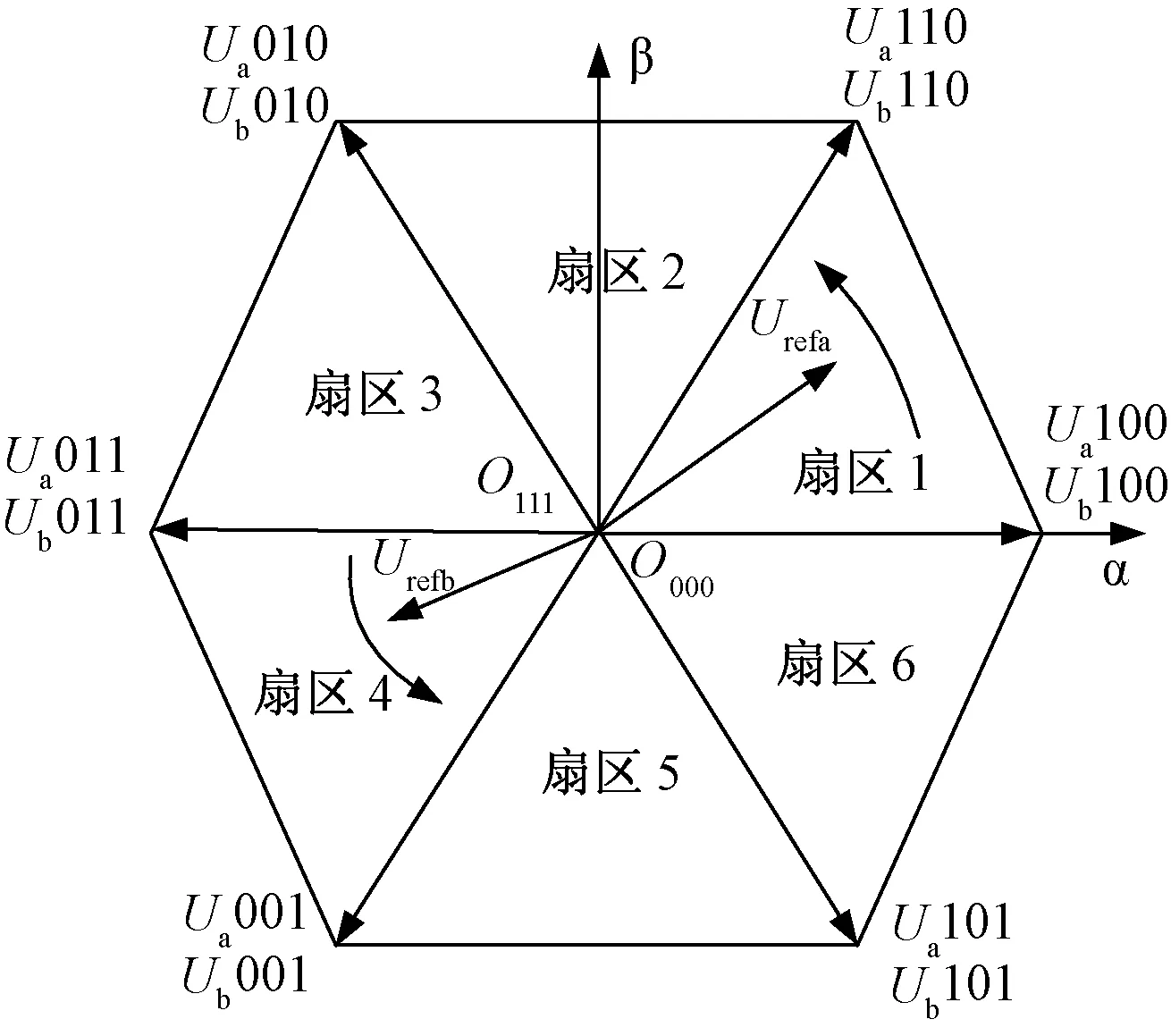
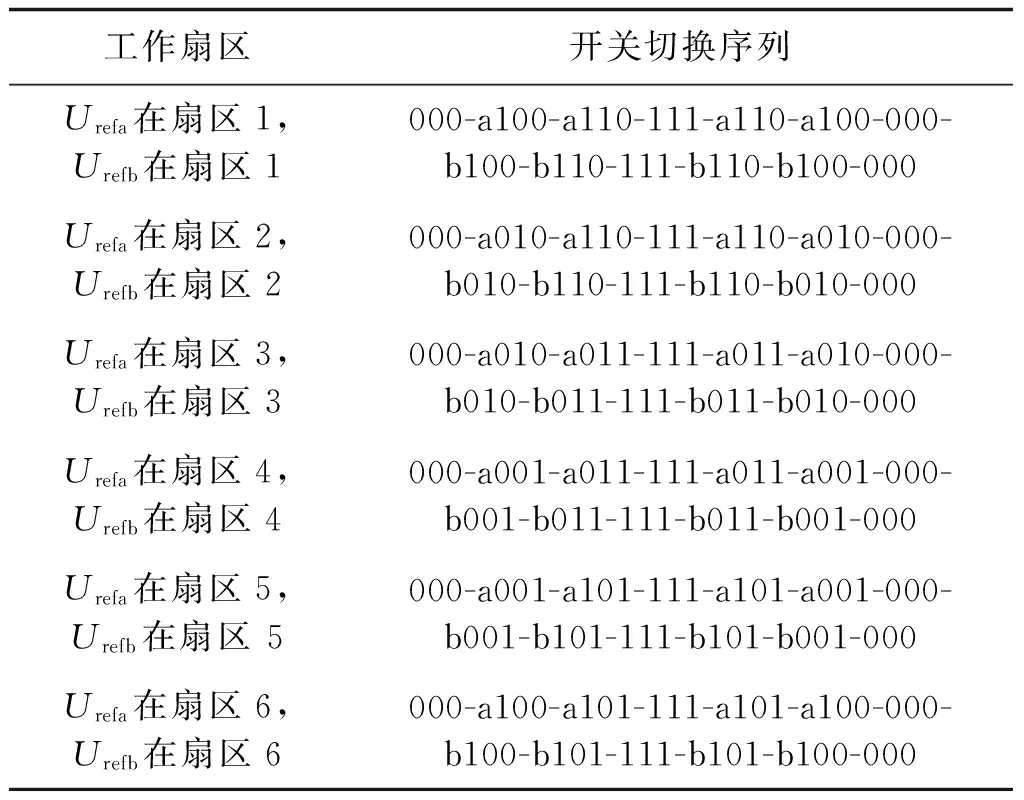
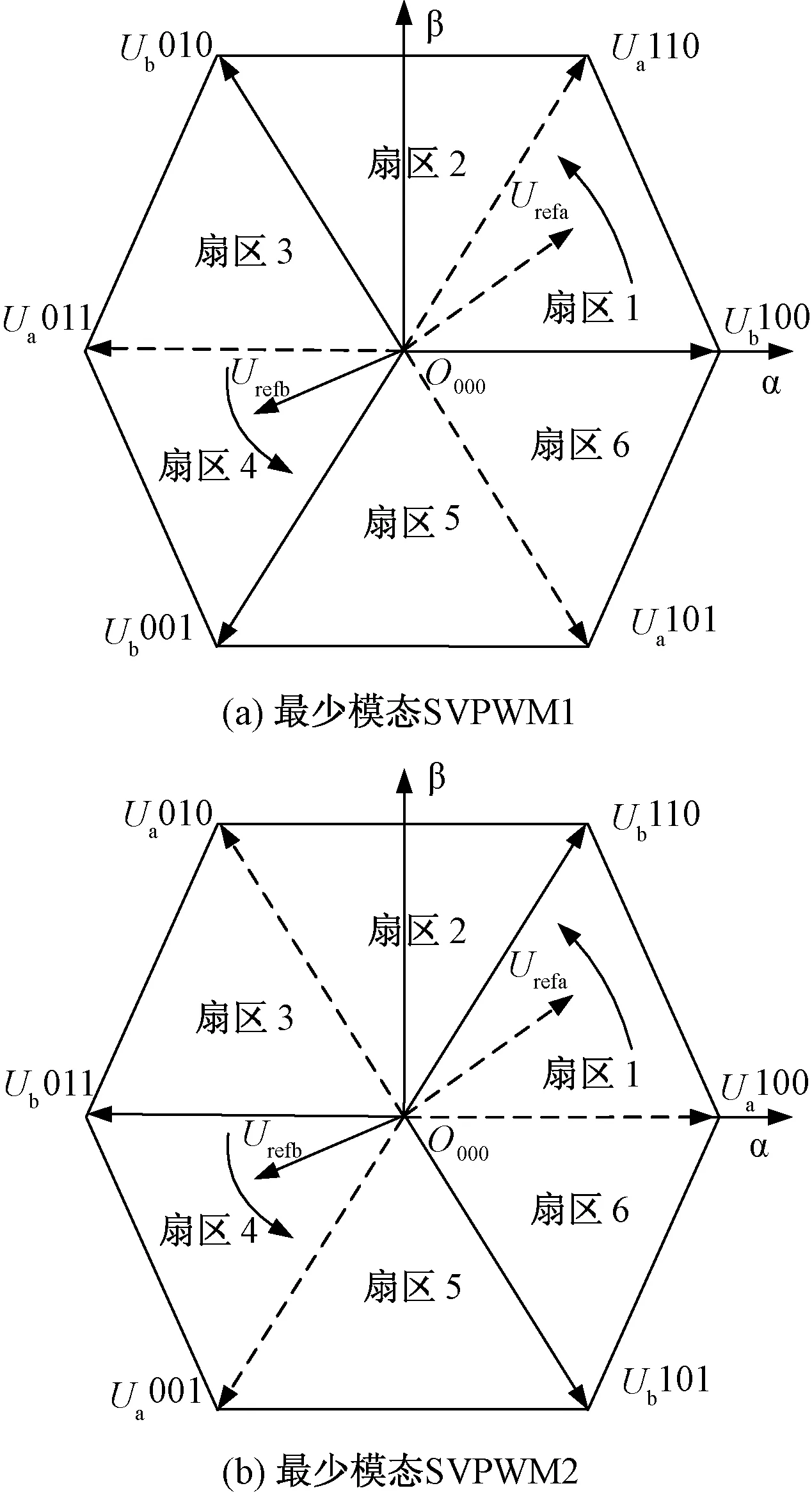
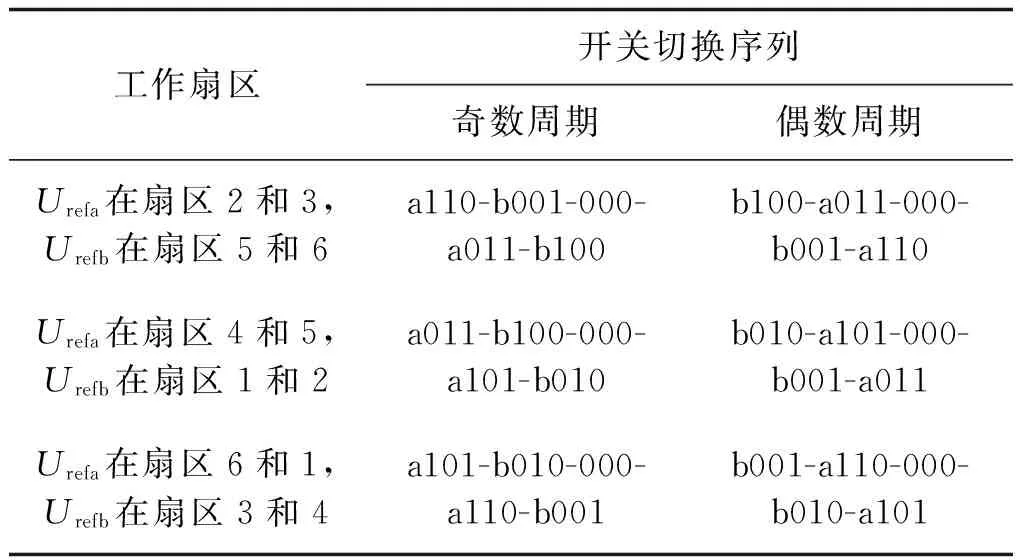
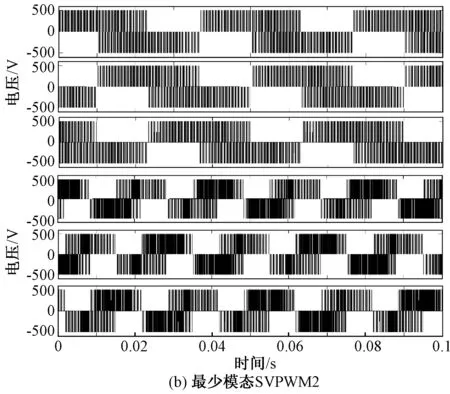
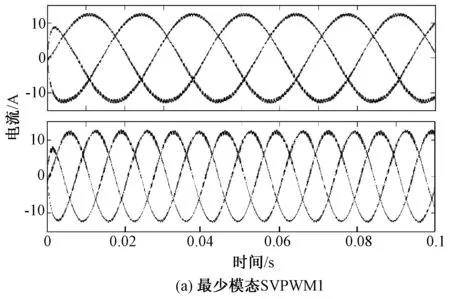
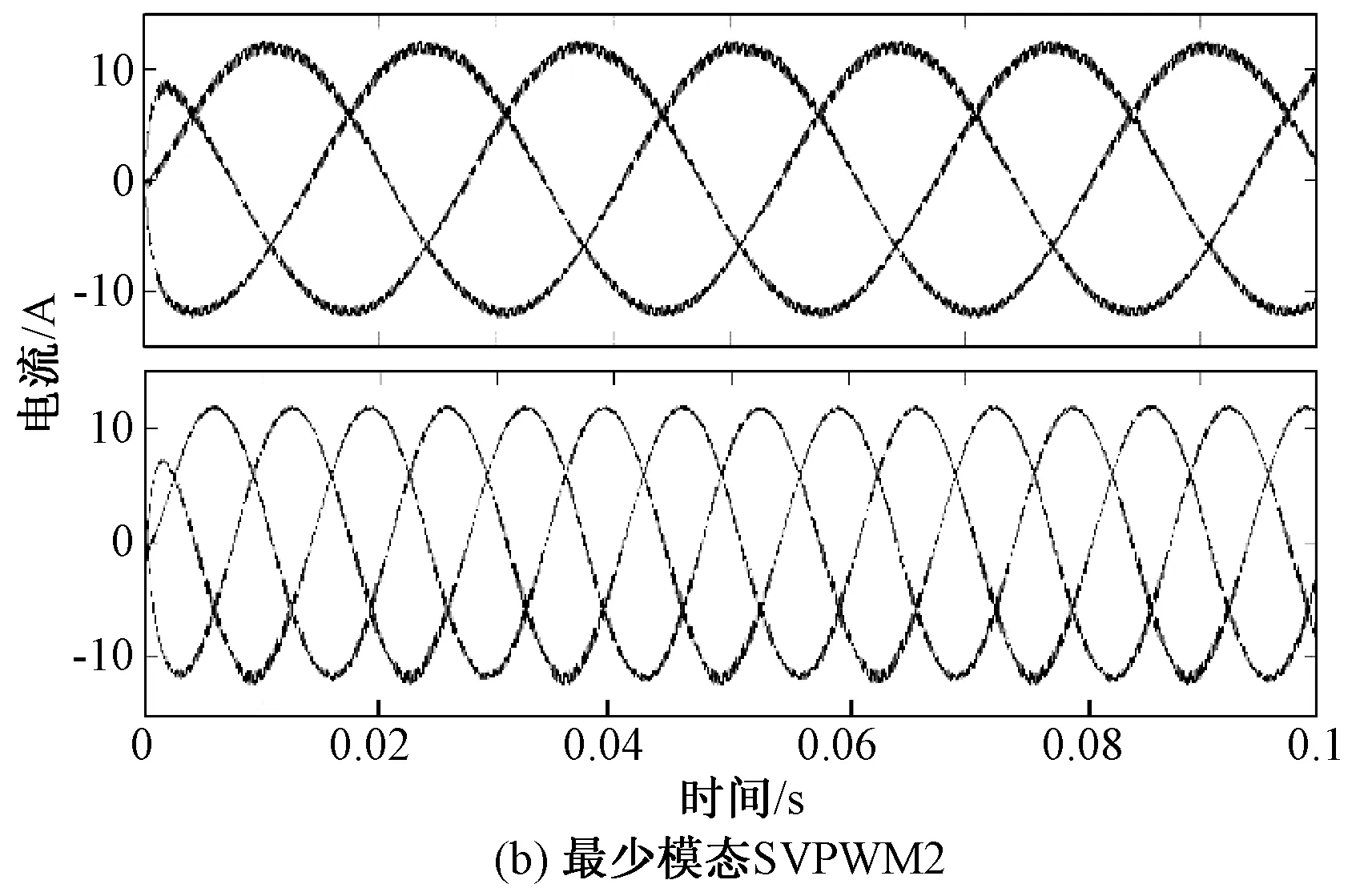
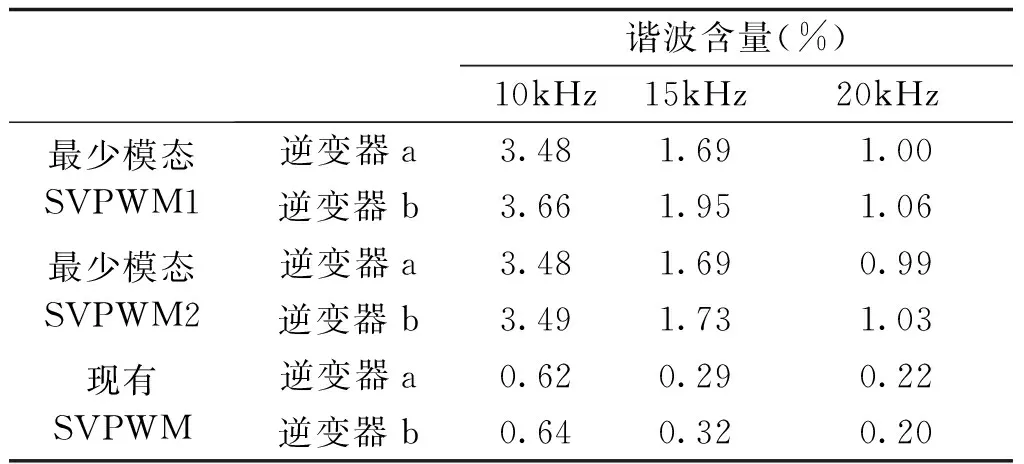
定义1(最少模态可控)：对于切换线性系统式(1)，在初始状态x0≠0的状况下，如果存在输入u和切换序列σ，使得系统仅使用m(m

最少模态可控的电力变换器在适当的调制策略下能够仅用m个模态合成所需要的输出波形，因此，研究五桥臂逆变器的最少模态可控性从而找出使系统状态可控的最少数量的工作模态，将能够极大地简化系统的调制方案。另一方面，由于所使用的工作模态减少，所以开关的切换序列可以得到简化，切换次数减少，效率将得到提升。然而，变换器正常工作所需的工作模态数量并不确定，所以为了使用最少的开关模态进行控制，最重要的是先找出使系统可控所必需的m个开关模态。

定理1：对于切换线性系统式(1)，如果其可控集C是全空间，即wn=Rn，则该系统称为最少模态可控。

五桥臂逆变器的切换线性系统模型如式(1)～式(6)所示。对该系统应用定理1，求取其可控集，则逆变器的线性子空间可以表述如下：

w1=〈A1|B1〉+〈A2|B2〉+…+〈A14|B14〉

=span{B1,B2,…B14,AB1,AB2,…,A2B14,…AnB14}

⋮

经过简单计算之后，可以得到：

dim(w1)=dim(w2)=…=dim(wn)=12

因此，wn=R12，这就是说系统的可控集合是整个向量空间。根据定理1，五桥臂逆变器在SVPWM调制下是完全状态可控的。由以上结果进一步分析五桥臂逆变器的最少模态可控性，可以得到：

分析结果表明，可控状态集可以由几个线性无关的向量张成，这几个向量分别为工作模态Ua110,Ua011,Ua101,Ub100,Ub010,Ub001；也可以是Ua100,Ua010,Ua001,Ub110,Ub011,Ub101。显然，不管对于何种组合，都只需要6个工作模态就能使可控状态集满秩，即五桥臂逆变器仅需要6种工作模态就能使系统状态可控。

4 最少工作模态SVPWM策略

4.1 现有SVPWM控制

由表1可知，现有的SVPWM的12个非零矢量以及2个零矢量分别对应了五桥臂逆变器的14个工作模态。五桥臂逆变器的现有SVPWM控制空间矢量图如图2所示。其中旋转矢量Urefa和Urefb分别代表逆变器a和逆变器b的三相电压的合成矢量。Urefa和Urefb分别由逆变器a和逆变器b的矢量合成，由于两个逆变器的矢量相互独立[2]，因此工作时逆变器互不干涉。

图2 五桥臂逆变器的现有SVPWM控制空间矢量图Fig.2 Space vector diagram for traditional SVPWM

为了同时对两个逆变器进行控制，在一个开关周期中，五桥臂逆变器的开关序列必须同时包含两个逆变器的开关序列，其具体实现如表2所示。若Urefa位于扇区1、Urefb位于扇区3时，五桥臂逆变器的开关序列应该由Urefa在扇区1的开关序列与Urefb在扇区3 的开关序列组合而成，即000-a100-a110-111-a110-a100-000-b010-b011-111-b011-b010-000，相当于逆变器a以其在扇区1的开关序列000-100-110-111-110-100-000进行切换，而逆变器b此时的开关序列则为其在扇区3 的序列000-b010-b011-111-b011-b010-000[3]。当处于其他扇区时，应根据两个参考矢量所处的区域选择对应的开关序列。在每一个载波周期中，五桥臂逆变器的开关状态总共要切换12次，这么繁复的切换必然导致开关频率增加，损耗增大，严重限制了系统的工作频率。

表2 现有SVPWM的开关切换序列Tab.2 Switching sequences of traditional SVPWM

4.2 最少模态SVPWM控制策略

第2节证明了五桥臂逆变器仅需要工作模态Ua110,Ua011,Ua101,Ub100,Ub010,Ub001或工作模态Ua100,Ua010,Ua001,Ub110,Ub011,Ub101两种工作模态组合就能使系统状态可控。因此，可以用6个工作模态为五桥臂逆变器设计新的调制策略，即最少模态SVPWM。其实现方案有两种，最少模态SVPWM1和最少模态SVPWM2，矢量分布图如图3所示。

图3 五桥臂逆变器型最少模态SVPWM控制空间矢量Fig.3 Space vector diagrams of m modes SVPWM control of five-leg inverter

由图3可以看出，最少模态SVPWM不再由14个空间矢量来合成参考矢量，仅使用6个空间矢量，即每一个逆变器仅用3个空间矢量来进行调制。

本文以最少模态SVPWM1方案为例说明最少模态SVPWM的实现算法。图3(a)给出了最少模态SVPWM1的空间矢量分布，其中3个为逆变器a的空间矢量，3个为逆变器b空间矢量。与现有的SVPWM相比，减少空间矢量之后，每一个逆变器矢量分布仅有三个扇区，对于最少模态SVPWM1，Urefa扇区为扇区2和3(60°～180°)、扇区4和5(180°～300°)、扇区6和1(300°～60°)，Urefb扇区为扇区1和2(0°～120°)、扇区3和4(120°～240°)、扇区5和6(240°～360°)，参考矢量的位置确定相对简单。

矢量作用时间的计算仍旧遵从平行四边形合成法则，但由于使用的矢量不再相同，计算过程会有差异。如Urefa在扇区2和3均由Ua110和Ua011合成，在扇区2和3的表达式均如式(7)所示，而现有SVPWM在每个小扇区均分别计算，如在扇区2和3的时间计算如式(8)和式(9)所示。

(7)

(8)

(9)

式中，T1、T2分别为有效矢量作用时间；T0为零矢量作用时间。

最少模态SVPWM1调制下，逆变器所用的空间矢量减少了一半，因此其计算复杂度有所降低，且开关切换序列可以得到极大的简化，具体开关序列如表3所示。

表3 最少模态SVPWM1开关切换序列Tab.3 Switching sequences of m modes SVPWM1

为了确保即使在切换周期的边界不存在多个相位的同时切换，在每两个载波周期中交替使用逆时针和顺时针序列。 因此，奇数周期和偶数周期的切换方案不同。例如，表3中扇区2和3中的Urefa在奇数周期中，逆变器a的切换序列为a110-000-a011，而偶数周期中的切换序列为a011-000-a110。类似地，在Urefb的扇区5和6中，逆变器b的切换序列也被设计为奇数周期中的b001-000-b100和偶数周期中的b100-000-b001。这种开关切换方案与现有SVPWM相比，功率器件开关的数量减少了2/3。

5 验证分析

为验证所提出最少模态SVPWM的可行性，使用Simulink搭建模型进行分析，具体电路参数如下：直流电压幅值为500V，La=Lb=Lc=4mH，Ca=Cb=Cc=10μF，两个输出负载参数一致，输出电压的频率分别为25Hz和50Hz，载波频率为10kHz，仿真步长为10-6s。验证结果如图4所示。

图4 最少模态SVPWM调制下五桥臂逆变器桥臂电压波形Fig.4 Bridge voltage waveforms of five-leg inverter modulated by m modes SVPWM

图4为五桥臂逆变器在最少模态SVPWM调制下的桥臂电压波形。其中上半部分为负载a三相电压波形，下半部分为负载b的三相电压波形。可以看出，两种新型调制策略均可实现两个负载不同频率下的正常工作，说明五桥臂逆变器在新型调制策略下能够同时对两个三相负载进行独立调制。

逆变器在最少模态SVPWM调制下的电流波形如图5所示。其中上半部分为负载a三相电流波形，下半部分为负载b三相电流波形。两种最少模态SVPWM调制下，逆变器两组负载的电流波形频率均明显不同，且其正弦度都较高，说明本文所提方法能够满足五桥臂逆变器的工作要求。

对电流波形进行谐波分析，结果如表4所示。可以看出，两个负载的电流波形谐波含量相当接近，且均能符合实际需求。在与现有的SVPWM谐波含量的比较中发现，虽然新型最少模态SVPWM的谐波含量要大于现有SVPWM，但是，随着开关频率的增加，两者的差距越来越小。

图5 最少模态SVPWM调制下五桥臂逆变器电流波形Fig.5 Output current waveforms of five-leg inverter modulated by m modes SVPWM

谐波含量(%)10kHz15kHz20kHz最少模态SVPWM1逆变器a3.481.691.00逆变器b3.661.951.06最少模态SVPWM2逆变器a3.481.690.99逆变器b3.491.731.03现有SVPWM逆变器a0.620.290.22逆变器b0.640.320.20

在调制度一致且负载相同条件下，公共桥臂的电流波形如图6所示。最少模态SVPWM的公共桥臂电流与现有SVPWM基本无异。因此在新型调制策略控制下，逆变器开关管通过的电流与现有SVPWM相比并无明显区别。

图6 不同调制策略下的公共桥臂电流波形Fig.6 Current waveform of common bridge under different modulation strategies

对不同调制策略下五桥臂逆变器的开关动作次数进行统计，以0.2s为计数周期，其结果如表5所示。随着工作频率的增加，现有的SVPWM调制下的开关动作次数远大于最少模态SVPWM，且总的开关次数差距越来越大。

相比现有的SVPWM策略，最少模态SVPWM算法在相同载波频率下仅使用一半数量的工作模态就可以产生相同的输出，这就意味着，仅用6个工作模态也能实现系统可控，从而验证了最少模态可控性理论，也验证了最少模态SVPWM策略的可行性。虽然最少模态SVPWM调制策略缩短开关序列后谐波含量不可避免地会有所增加，但其开关动作频率降低的效果更为显著，且随着工作频率的提升，优势更加明显。因此，最少模态SVPWM更适用于高频开关频率下的调制。

表5 不同工作频率下的开关次数分析Tab.5 Switching times analysis under different working frequency

6 结论

本文分析了五桥臂逆变器在SVPWM调制下的工作模态，将其建模为切换线性系统模型；利用所建立的模型，研究了五桥臂逆变器的可控性。对于完全状态可控的五桥臂逆变器，本文从逆变器所有工作模态中找出6个工作模态，使得整个系统仅使用6个工作模态就能够实现完全可控；并在此基础上提出一种旨在降低开关频率的最少模态SVPWM策略。与现有SVPWM方法相比，在相同载波频率下产生相同的输出波形，新的调制策略使用的工作模态减少了一半，实现复杂程度降低，且其开关器件的切换次数减少了2/3。因此新的控制策略不仅易于实现，而且能够有效地降低开关损耗，提高系统的工作效率。

参考文献(References)：

[1] François B, Bouscayrol A. Design and modeling of a five-phase voltage-source inverter for two induction motors[A]. EPE Conference[C]. 1999.

[2] Hizume M, Yokomizo S, Matsuse K. Independent vector control of parallel connected two induction motors by a five-leg inverter [A]. European Power Electronics and Applications Conference[C]. Toulouse, France, 2003. 778.

[3] Jones M, Dujic D, Levi E. A performance comparison of PWM techniques for five-leg VSIs supplying two-motor drives [A]. 2008 34th Annual Conference of IEEE Industrial Electronics [C]. Orlando, FL, USA, 2008. 508-513.

[4] 刘嘉,梅杨,王莉娜,等(Liu Jia, Mei Yang, Wang Lina, et al.). 五桥臂逆变器驱动双异步电机调速系统的调制方法研究(Research on modulation method of five-leg inverter fed dual induction motor drive system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2012, 31(2):42-46.

[5] Dixit A, Mishra N, Sinha S K, et al. A review on different PWM techniques for five leg voltage source inverter[A]. IEEE-International Conference on Advances in Engineering, Science and Management [C]. 2012. 421-428.

[6] Ezzine Jelel, Haddad A H. On the controllability and observability of hybrid systems [A]. American Control Conference[C]. 1988. 41-46.

[7] Muhammad Mansoor Khan, Wu Zhiming. Modeling PWM DC-DC converter as discrete input/continuous output system and its application to system local controllability [A]. The 27th Annual Conference of the IEEE Industrial Electronics Society [C]. 2001. 2:826-831.

[8] Xie G M, Zheng D Z, Wang L. Controllability of switched linear systems [J]. IEEE Transactions on Automatic Control, 2002, 47(8):1401-1405.

[9] Hu Zongbo, Zhang Bo, Deng Weihua. Output controllability of switched power converters as switched linear systems [A]. The 4th International Power Electronics and Motion Control Conference [C]. 2004. 3:1665-1668.

[10] Xu Zhiyu, Yu Youling, Xu Weisheng, et al. Controllability of nonisolated DC-DC converters with constant-power-load [A]. 2012 24th Chinese Control and Decision Conference [C]. 2012. 669-673.

[11] Li X, Zhang B, Qiu D. Three-mode pulse-width modulation of a three-phase four-wire inverter [J]. IET Power Electronics, 2015, 8(8): 1483-1489.

[12] Li Xiangfeng, Zhang Bo, Qiu Dongyuan. A novel PWM strategy for three-phase inverters based on controllability theory[A]. IECON 2013 - 39th Annual Conference of the IEEE Industrial Electronics Society[C]. 2013. 298-303.

[13] Li X, Zhang B, Qiu D, et al. New PWM strategy for nine-switch inverters with minimum number of semiconductor switching[A]. 2014 International Power Electronics and Application Conference and Exposition[C]. Shanghai, China, 2014. 406-410.