T参数模型及其在S/P补偿WPT系统中的应用

辛平平， 周冀松， 丰 骏， 陈乾宏

(1. 南京航空航天大学, 江苏 南京 211106； 2. 南京机电液压工程研究中心, 江苏 南京 211106； 3. 南通江海电容器有限公司， 江苏 南通 226361)

1 引言

从1890年特斯拉的演示实验[1]之后，人们便开始了对无线电能传输(Wireless Power Transfer，WPT)技术的不断探索。得益于半导体器件和电力电子技术的发展，在应用需求的推动下，无线电能传输技术得到了很大的发展。其应用领域覆盖了长航时飞行器、人体植入设备、传感器网络、便携设备充电器以及电动汽车充电等诸多领域[2-4]。

根据能量耦合单元的耦合方式的不同，无线电能传输可以分为四种方式[5]，即电磁辐射式[6]、电场耦合式[7,8]、磁场耦合式[9,10]和超声波式[11]。典型的无线电能传输系统结构组成如图 1所示。

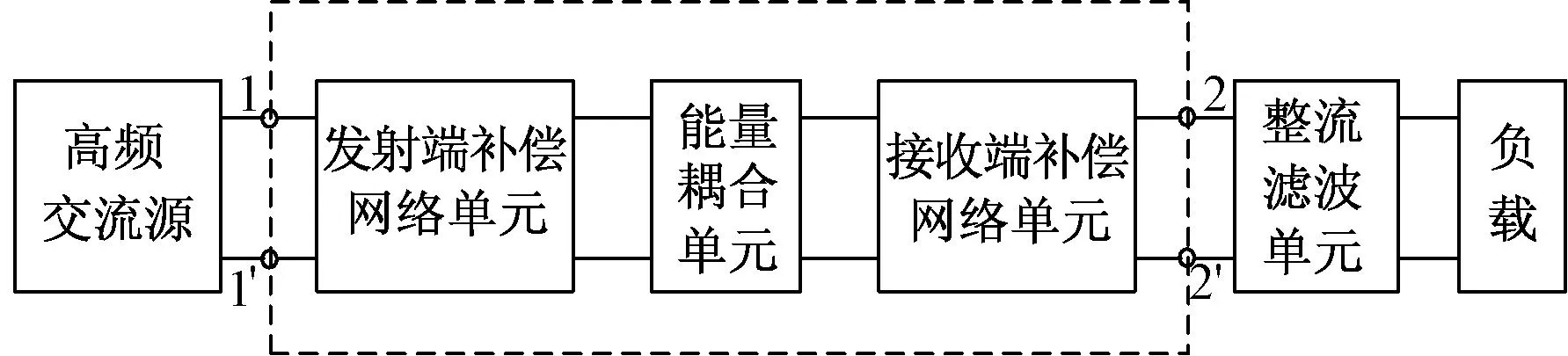
图1 WPT系统典型结构Fig.1 Typical structure of WPT system

为了研究WPT 系统的特性，研究人员给出了多种建模方法。目前常用的WPT系统的分析模型主要有耦合模模型[12]、互感模型[13,14]以及二/多端口网络模型[15,16]。文献[12]使用耦合模模型建立得到磁场耦合式WPT系统的高阶数学模型，但是模型的建立过程较为复杂，且模型不能直接反映系统中的电参数关系。文献[13]采用理论计算方法计算发射和接收线圈的电路参数，根据电路的互感模型，分析磁场耦合式 WPT系统的特性；但理论计算不仅较复杂，同时还常常忽略元件的寄生参数。文献[15]建立了磁场耦合式WPT的T参数模型，并通过阻抗匹配技术，优化了WPT系统的功率传输性能，但并未基于T参数模型研究系统的工作特性。

考虑到WPT系统可视作由二端口网络级联而成，而二端口网络模型中T参数模型最适用于级联网络系统的建模和分析。因此，本文采用T参数模型对WPT系统进行建模和分析，并对模型参数的获取，以及如何结合具体变换器进行应用展开研究。最后以串/并(S/P)结构的WPT系统为例，进行理论分析与实验验证。

2 T参数模型及其参数的获取方法

二端口网络模型通常可以描述一端输入而另一端输出的电路。描述二端口网络的参数模型有T参数、Z参数、Y参数和S参数模型等。其中T参数模型以输出端的U2、I2为自变量，输入端的U1、I1为因变量，所以T参数模型适用于级联网络的建模和分析[14,17]。

WPT系统的二端口网络模型包括了发射端和接收端的补偿单元以及能量耦合单元，如图 2所示。WPT系统由这三个网络单元级联而成，故应用T参数模型可简化WPT系统的建模过程，同时T参数模型作为一种端口网络模型，电路中分布参数的影响已经自然体现在模型参数中，是高频电子线路中常用的建模方法。因此本文选取T参数模型对WPT系统进行分析。

图2 WPT系统的二端口网络模型Fig.2 Two-port network model of WPT system

WPT系统T参数模型的获得，一方面可由发射端和接收端的补偿单元网络以及能量耦合单元网络各自的T参数模型依次相乘得到，另一方面也可以将三个级联网络视作一个整体，获得其T参数模型。图2的WPT系统采用T参数模型可以表示为：

(1)

WPT系统T参数模型各个参数的获取方法有多种。常用的方法即依据式(2)，将三个级联单元视作一个整体，在端口2进行开短路测量，再由计算获得模型参数。这种方法需要采用网络分析仪，而且在端口2进行短路测量，即令U2=0时，可能会使得I2或I1过大，有损坏仪器设备的风险。

(2)

另一种常用的模型参数获取方法则是从电路理论出发，在已知电路网络拓扑和元器件的参数条件下计算得到模型参数。这种方法不如端口网络参数获取方法便捷，且高频时，元器件的寄生参数和电路中的分布参数会改变电路的网络拓扑结构，影响模型参数的准确获取。

为了保证模型参数获取的便捷性，并避免短路测试损坏设备，本文采用了特定负载条件下的二端口网络增益特性测试结合理论计算的方法来确定模型参数。下面具体说明其参数的获取方法。

首先，在端口2接不同的负载RL1、RL2，可以测得端口2相对端口1的电压增益分别为G21、G22，G21、G22与模型参数的关系为：

(3)

同理，在端口1接不同的负载RL1和RL2，可以测得端口1对端口2的增益分别为G11、G12，G11、G12与模型参数的关系为：

(4)

联立式(3)和式(4)可以得到：

(5)

3 T参数模型在S/P补偿的WPT系统中的应用

3.1 系统工作特性分析

WPT系统发射端或接收端的视在功率为：

(6)

式中，S为端口的视在功率；U和I分别为端口电压和电流。

由此可以得到端口的有功功率P为：

P=Re(UI*)

(7)

当端口2的负载RL为阻性时，根据图 2的参考方向，端口2的电压U2和电流I2关系为：

U2=-I2RL

(8)

根据式(4)和式(8)，可以得到式(9)和式(10)：

(9)

(10)

式中，U1和I1分别为端口1的电压和电流；G2为端口2对端口1的电压增益。

由式(9)可以得到效率η的表达式：

(11)

对式(11)求极值，可得到最高效率ηmax及其对应的负载条件，如式(12)和式(13)所示：

(12)

(13)

由T参数模型可变换得到戴维南等效电路，如图 3所示，并可得到系统的输出功率Po：

(14)

图3 二端口网络的戴维南等效电路图Fig.3 Thevenin equivalent circuit of two-port network

对式(14)求导，可得到最大输出功率及其对应的负载条件，分别如式(15)和式(16)所示。

(15)

(16)

由式(10)～式(16)可以看出，采用T参数模型后，WPT系统的电压增益、传输功率和传输效率有通用的表达式，与补偿拓扑的选择无关。补偿拓扑的不同只是影响T参数模型中各个参数的取值。

下面结合S/P补偿WPT系统开展研究。

3.2 S/P补偿WPT系统的T参数模型

S/P补偿WPT系统的基波等效电路如图4所示。其中C1、C2分别为发射、接收侧的补偿电容，R1、R2和L1、L2分别为发射、接收线圈的内阻及自感，M为发射、接收线圈之间的互感。发射端补偿单元、接收端补偿单元以及能量耦合单元的T参数矩阵如表1所示。

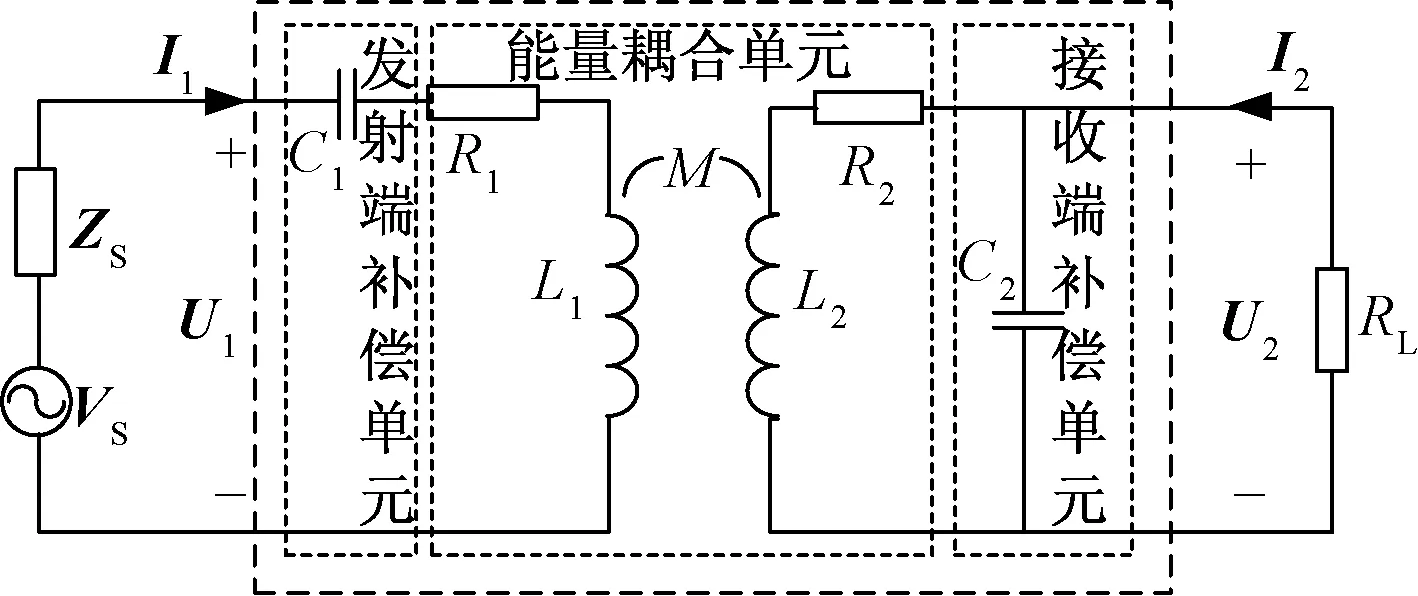
图4 S/P补偿WPT系统Fig.4 S/P compensated WPT system

单元种类T参数矩阵发射端补偿单元11jωC101éëêêêùûúúú能量耦合单元R1+jωL1jωM(R1+jωL1)(R2+jωL2)+ω2M2jωM1jωMR2+jωL2jωMéëêêêùûúúú接收端补偿单元10jωC21[]

将表1中三个T参数矩阵相乘即可得到WPT系统的T参数模型，如式(17)所示：

(17)

式中

为了实现高效率并使输出增益对负载不敏感，S/P补偿网络通常工作于调谐模式[18]，即满足式(18)，根据式(11)可以求得调谐时S/P补偿网络的效率，如式(19)所示：

(18)

(19)

4 实验结果与讨论

为了验证T参数模型对于WPT系统特性描述的适用性和模型参数获取方法的准确性，本文搭建了S/P补偿WPT系统的实验装置，其原理图如图5所示，实验平台装置如图 6所示。由实际的负载电阻Ro可推得基波等效负载RL为：

(20)

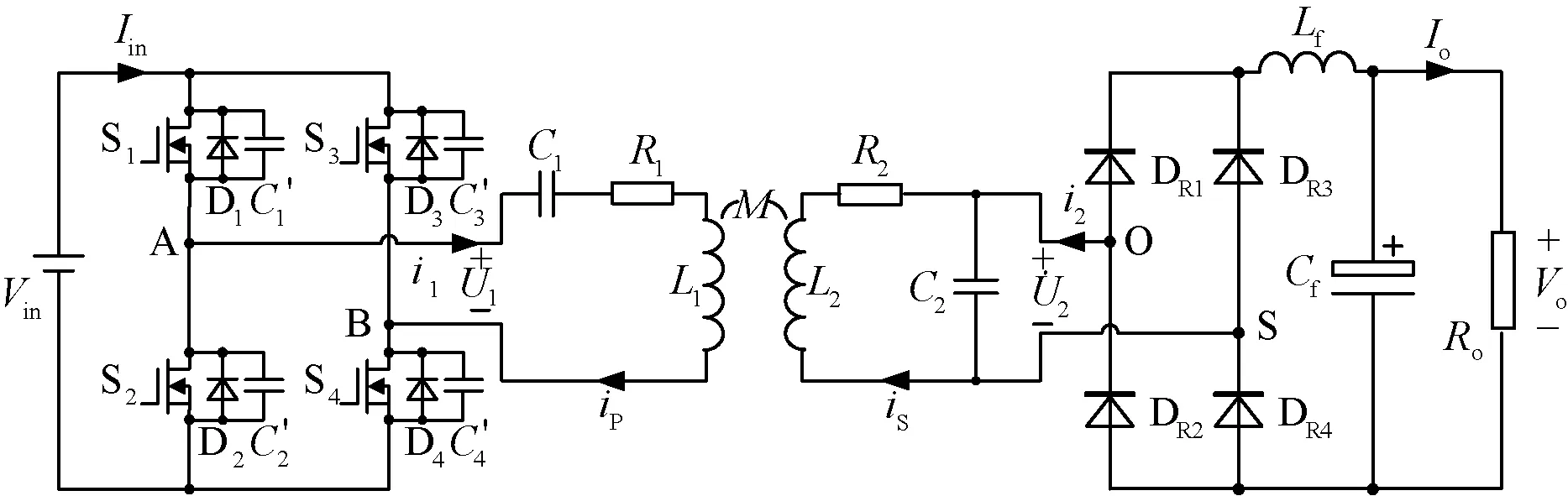
图5 S/P补偿WPT系统电路原理图Fig.5 Schematic diagram of S/P compensated WPT system

图6 S/P补偿WPT系统实验样机图Fig.6 Prototype of S/P compensated WPT system

利用LCR测试仪，在频率为85kHz时，可测得发射线圈和接收线圈的自感L1、L2分别为99.39μH、99.75μH，互感M为39.9μH，补偿电容C1=34.0nF、C2=34.0nF。

4.1 S/P补偿WPT系统的T参数模型的获取

根据测试得到的元件参数，由式(17)可建立系统的T参数模型。具体模型参数的幅频/相频曲线如图7所示。

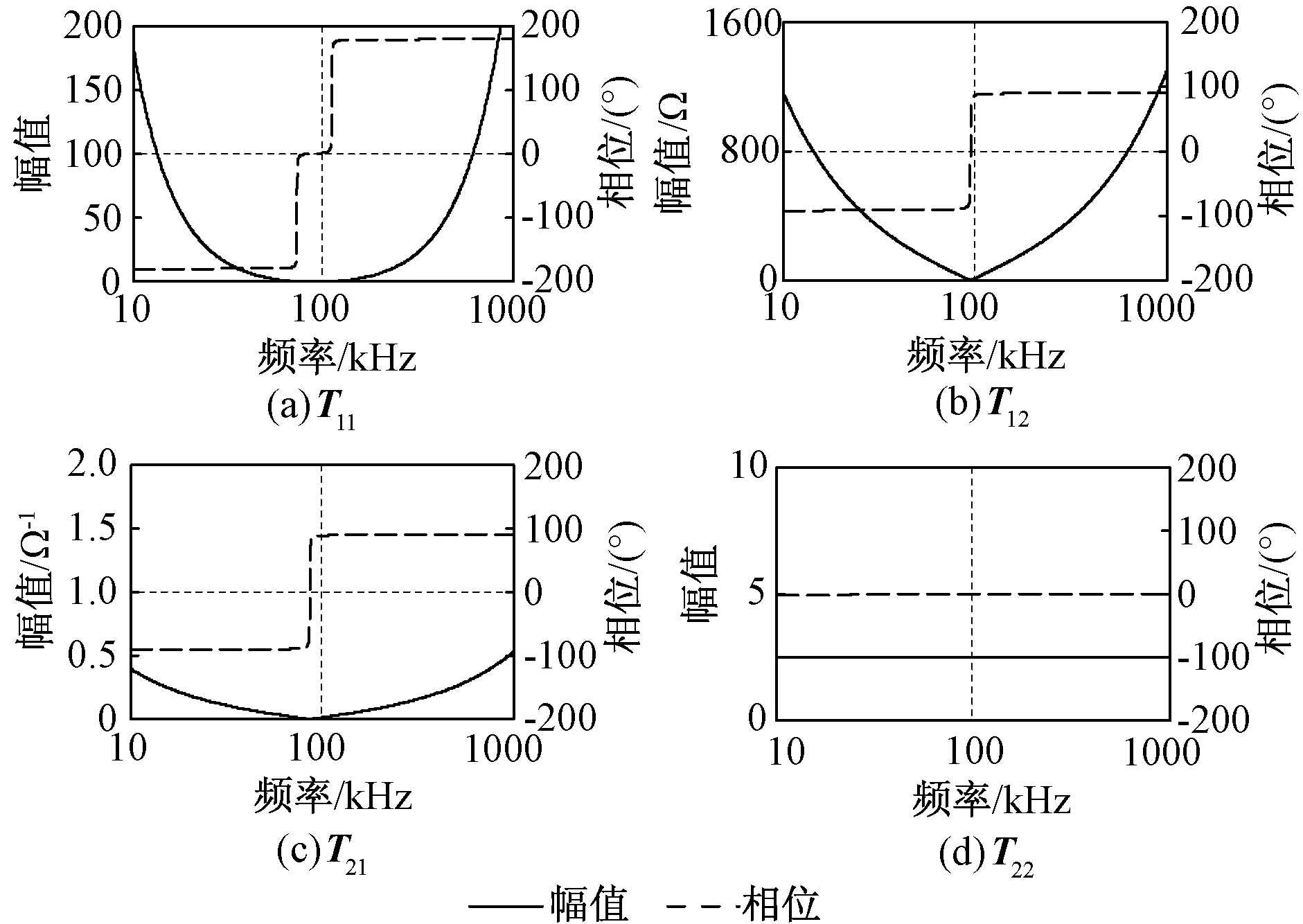
图7 由式(17)得到的T模型参数的幅频/相频曲线Fig.7 Amplitude-frequency/phase-frequency curves of T model parameters according to (17)

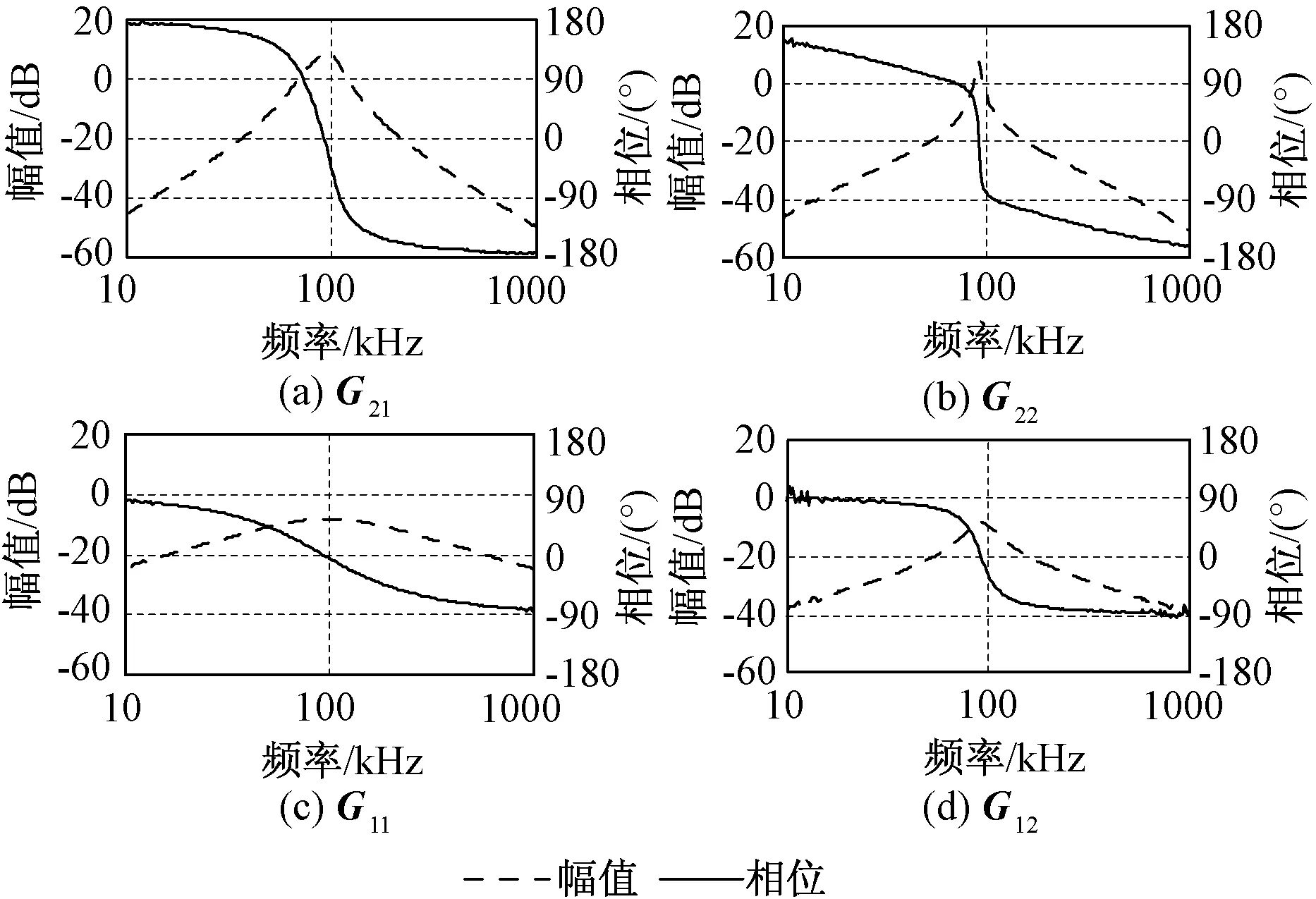
图8 电压增益波特图Fig.8 Bode diagrams of voltage gains

基于二端口网络增益特性测试结果，由式(3)、式(4)也可得到系统的T参数模型。令RL1=75Ω、RL2=15Ω，利用网络分析仪E5061B可测量得到4个电压增益特性曲线，如图8所示。将各个电压增益代入式(5)，可以得到WPT系统T参数模型各个参数的幅频和相频特性曲线，如图9所示。

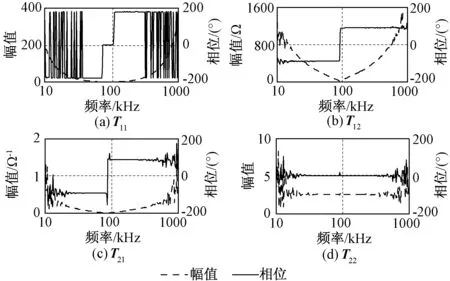
图9 基于增益测试获得的T模型参数的幅频/相频曲线Fig.9 Amplitude-frequency/phase-frequency curves of T model parameters based on gain measurement

比较图7、图9可以看出，两种方法得到的具体模型参数的幅相曲线形状相似。图9曲线中的毛刺是网络分析仪测试结果的反映。

4.2 工作特性的理论分析与实验结果

下面将使用4.1节得到的两种模型参数，结合3.1节的分析结果来分析S/P系统的工作特性，并与实验结果进行对比。

工作频率为86.2kHz和100kHz时，S/P系统的输出功率、传输效率随实际负载变化的理论分析与实验测试结果分别如图10、图11所示。

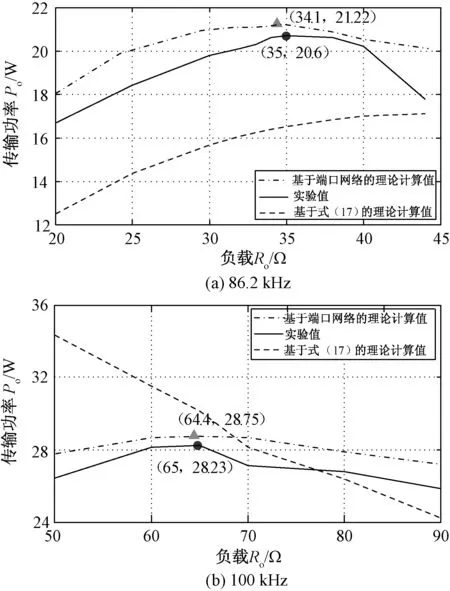
图10 不同频率时输出功率随负载的变化曲线Fig.10 Curves of output power versus load at different operation frequencies

对比两种理论分析结果和实验测试结果，可以看出，基于增益测试所得模型参数的理论分析结果与实验测试结果的变化规律基本相同，除了86.2kHz的效率分析结果误差略大外，与实验测试结果吻合较好。而基于式(17)的理论计算结果与实验值误差较大，这主要有两个原因：①元件测试在特定频率，不能反映频率变化的影响；②由元件参数计算得到模型参数是基于特定的补偿方式和拓扑结构，高频工作时，电路分布参数和元件寄生参数的存在会使得电路的拓扑结构发生一定变化，从而影响模型参数的获取和相关特性的精确分析。

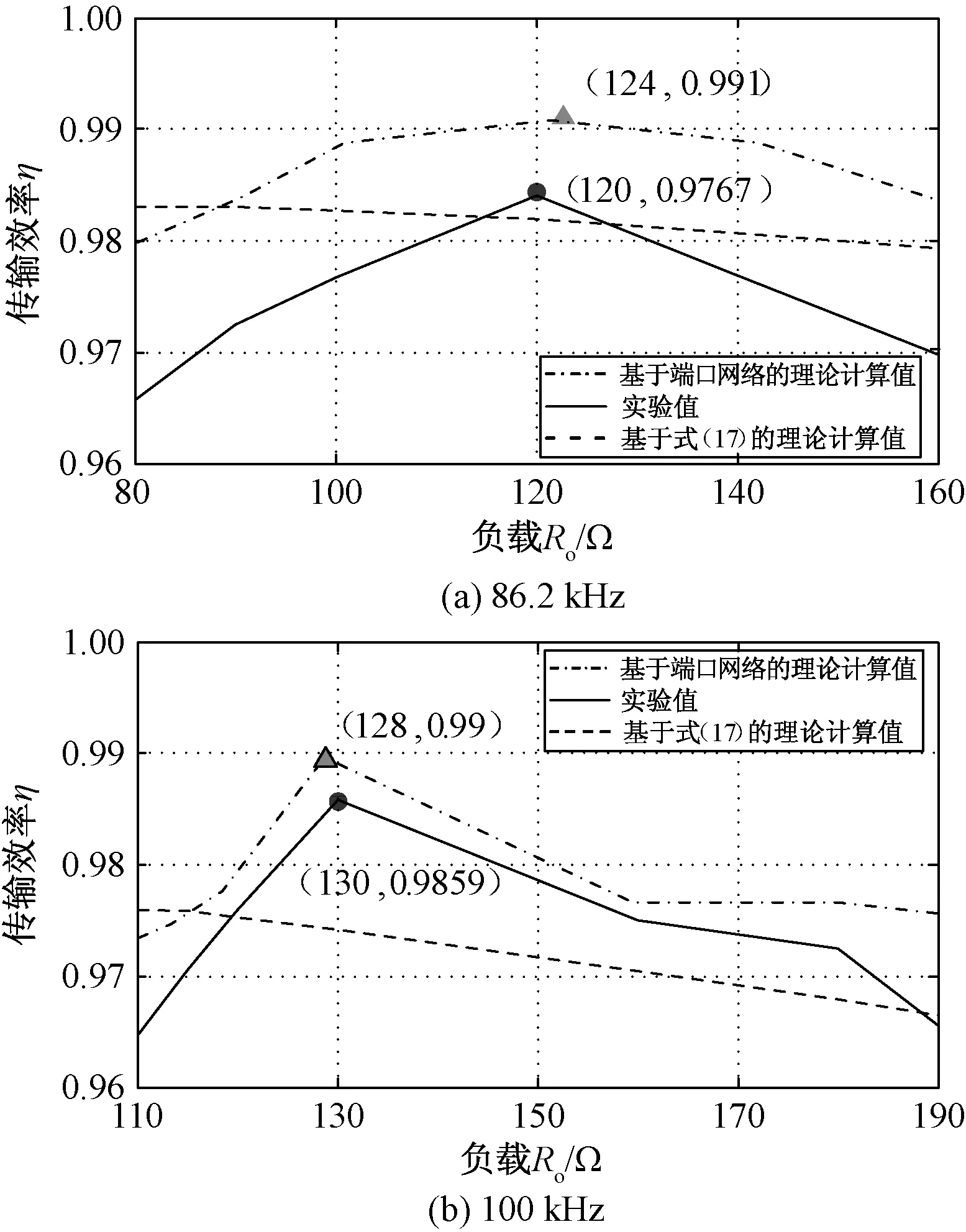
图11 不同频率时传输效率随负载的变化曲线Fig.11 Curves of efficiency versus load at different operation frequencies

基于增益测试所得模型参数，计算得到的输出功率和系统效率比实际测试结果略高，这是因为增益特性测试是在小信号条件下完成的。实际运行时，线圈电阻因发热变大，使得实测值低于理论计算值。

根据式(15)、式(20)，采用二端口网络增益测试获得的T模型参数，可求出86.2kHz和100kHz时，最大传输功率对应的实际负载电阻分别为34.1Ω和64.4Ω。根据图10的实验结果，最大输出功率对应的负载阻值为35Ω和65Ω。根据式(13)、式(20)，可求出当频率为86.2kHz和100kHz时，最高效率对应的阻值分别为124Ω和128Ω；而图11的实验测试结果为120Ω和130Ω。可见，最大输出功率或最高效率对应的最优负载电阻的理论分析结果与实验结果吻合良好，证明了理论分析的正确性。

5 结论

本文采用T参数模型对WPT系统进行建模，讨论了参数模型的获取方法，并在此基础上分析了WPT系统的工作特性，给出其工作特性的通用表达式。然后，通过二端口网络的增益特性测试和元器件参数测试计算的参数获取方法，分别得到了S/P补偿WPT系统的T参数模型。最后，通过对比计算的工作特性结果与实验测试结果，表明基于二端口网络增益测试获得T参数模型更为准确，验证了理论分析的正确性和参数获取方法的有效性。本文为采用T参数模型研究WPT系统的特性提供了参考。

参考文献(References)：

[1] Barrett J P. Electricity at the Columbian exposition[M]. Charleston: Nabu Press, 2013.

[2] Kurs A, Karakis A, Moffatt R, et al. Wireless power transmission via strongly coupled magnetic resonances[J]. Science, 2007, 317:83-86.

[3] 张巍，陈乾宏，曹玲玲(Zhang Wei, Chen Qianhong, Cao Lingling).植入式设备非接触电能传输系统的研究进展(Research review of the transcutaneous contactless power transmission system)[J].电源学报(Journal of Power Supply)，2011，9(4)：36-45.

[4] 曹玲玲，陈乾宏，任小永，等(Cao Lingling, Chen Qianhong, Ren Xiaoyong, et al.). 电动汽车高效率无线充电技术的研究进展(Review of the efficient wireless power transmission technique for electric vehicles)[J].电工技术学报(Transactions of China Electrotechnical Society)，2012，27(8)：1-13.

[5] 赵争鸣，张艺明，陈凯楠(Zhao Zhengming, Zhang Yiming, Chen Kainan).磁耦合谐振式无线电能传输技术新进展(New progress of magnetically-coupled resonant wireless power transfer technology)[J].中国电机工程学报(Proceedings of the CSEE)，2013, 33(3)：1-13, 21.

[6] Brown W C. The history of power transmission by radiowaves[J]. IEEE Transactions on Microwave Theory and Techniques, 1984, 32(9):1230-1242.

[7] Liu C, Hu A P, Nair N K C, et al. 2-D alignment analysis of capacitively coupled contactless power transfer systems[A]. IEEE Energy Conversion Congress and Exposition[C]. Atlanta, USA, 2010. 652-657．

[8] Yang C, Tsunekawa K. Analysis and performance improvement of independent electric coupled resonance WPT system with impedance transformer[A]. 2014 IEEE Wireless Power Transfer Conference[C]. 2014. 239-242.

[9] 陈文仙，陈乾宏，张惠娟(Chen Wenxian, Chen Qianhong, Zhang Huijuan).电磁共振式无线电能传输系统距离特性的分析(Distance characters analysis of magnetic resonance wireless power transmission system)[J].电力系统自动化(Automation of Electric Power Systems)，2015，39(8)：98-104.

[10] 罗斌，生茂棠，吴仕闯，等(Luo Bin, Sheng Maotang, Wu Shichuang, et al.).磁谐振耦合式单中继线圈无线功率接力传输系统的建模与分析(Modeling and analysis of magnetic resonance coupling wireless relay power transfer system with single intermediate coil resonator)[J].中国电机工程学报(Proceedings of the CSEE)，2013，33(21)：170-177.

[11] 邹玉炜，黄学良，柏杨，等(Zou Yuwei, Huang Xueliang, Bai Yang, et al.).基于PZT的超声波无接触能量传输系统的研究(Research on contactless ultrasonic energy transfer system based on PZT)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2011，26(9)：144-150.

[12] 张献，杨庆新，陈海燕，等(Zhang Xian，Yang Qingxin, Chen Haiyan, et al.).电磁耦合谐振式传能系统的频率分裂特性研究(Research on characteristics of frequency splitting in electromagnetic coupling resonant power transmission systems)[J].中国电机工程学报(Proceedings of the CSEE), 2012, 32(9):167-172.

[13] Hirayama H, Okuyama Y, Kikuma N, et al. Equivalent circuit of induction fed magnetic resonant WPT system[A]. 2011 IEEE MIT-S International Micorwave Workshop Series on Innovative Wireless Power Transmission: Technologies, System, and Application (IMWS) [C]. 2011. 239-242.

[14] Hou J, Chen Q, Ren X, et al. Steady-state analysis of series/series-parallel compensated contactless resonant converter[A]. 2014 IEEE 79th Vehicular Technology Conference (VTC Spring) [C]. Seoul, Korea, 2014. 1-5.

[15] 邱利莎，黄守道，李中启(Qiu Lisha, Huang Shoudao, Li Zhongqi).磁耦合谐振式无线输电系统的阻抗匹配研究(Research on impedance matching of wireless power transfer via coupled magnetic resonance)[J].电力电子技术(Power Electronics)，2015，49(10)：86-88.

[16] 王浩，王安娜，赵强，等(Wang Hao, Wang Anna, Zhao Qiang, et al.).基于散射矩阵的无线电能传输系统电磁耦合效率测量方法的研究(Research on electromagnetism coupling efficiency of wireless power transmission system based on scattering matrix)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2015，30(14)：463-469.

[17] Weber R J. 微波电路引论:射频与应用设计(Introduction to microwave circuits radio frequency and design applications) [M]. 朱建清(Zhu Jianqing)译. 北京：电子工业出版社(Beijing: Publishing House of Electronics Industry)，2005.

[18] Zhang Y, Chen Q, Ren X, et al. Design of S/P compensated IPT system considering parameter variations in consideration of ZVS achievement[A]. 2016 IEEE Energy Conversion Congress and Exposition (ECCE)[C]. 2016. 1-6.