下垂控制并网逆变器的孤岛检测机理研究

王晓寰， 杨庆收， 阚志忠， 王 琳

(电力电子节能与传动控制河北省重点实验室， 燕山大学电气工程学院， 河北 秦皇岛 066004)

1 引言

随着可再生能源发电技术的发展，分布式发电(DG)技术应运而生。分布式发电是指利用本地的化石类燃料和可再生能源(太阳能、风能等)等各种可用的分散存在的能源进行发电。可再生能源是分布式能源最清洁、最高效的利用方式[1]。近年来下垂控制的逆变器由于具有“即插即用”、无需通信等优点，在分布式发电系统中应用越来越广泛。目前国内外学者关于下垂控制的研究多集中于它的稳定性分析、运行模式之间的无缝转换以及下垂特性的改进等方面，很少有学者针对下垂控制并网逆变器的孤岛检测这个分布式并网系统必备的功能进行研究。

孤岛效应是指当电力系统因故障停止供电时，分布式发电系统继续向本地负载提供有功和无功功率的现象[2]。基于本地的孤岛检测方法包括被动检测方法和主动检测方法，其中被动检测方法包括过/欠压、过/欠频、相位跳变、谐波检测等，其主要特点是：①输出电能质量好，对电网无影响；②有些电量无法直接测量，必须通过复杂的计算获得；③在逆变器输出功率和本地负载所需功率匹配的情况下，检测盲区相对较大，检测时间也会加长；④适合于逆变器输出功率与负载所需功率不匹配的场合，一般都与主动孤岛检测方法相结合使用[3,4]。

主动检测方法包括阻抗测量法[5]、谐波阻抗测量法、频率偏移法、无功扰动法[6]、滑模频率偏移法[7]、sandia频率偏移法、sandia电压偏移法[8]。这些方法的检测原理基本相同，都是在并网系统的电流或电压中施加一个扰动量，将一个正常运行的系统推向非正常运行状态，从而检测出孤岛立即停止逆变器运行。

但是这些方法都是针对直接电流并网型逆变器提出的。文献[9]比较了恒功率控制的并网逆变器，给出了仅加入Q-V下垂控制、仅加入P-f下垂控制和同时加入P-f/Q-V下垂控制的孤岛检测盲区(NDZ)大小的方法，得到了加入下垂控制后孤岛检测盲区增大的结论。本文第2节详细计算了下垂控制的并网逆变器的被动孤岛检测算法的检测盲区，并给出了影响它的因素。

文献[10]研究了采用P-f/Q-V下垂控制的并网逆变器的孤岛检测方法，为了能够检测到孤岛，对下垂控制进行改进，将下垂系数由一个固定的数值改为PI调节器。文献[11]针对被动孤岛检测存在较大检测盲区，而主动检测方法会引起输出电流的有功或无功扰动的问题，提出将传统的下垂控制器中的频率指令改为逆变器并网点的实际频率。这两种方法检测到孤岛的前提都是对传统的下垂控制方法进行改进。本文针对传统的下垂控制并网逆变器进行研究，提出适用于传统P-f/Q-V下垂控制并网逆变器的孤岛检测方法，相较于文献[10, 11]而言，本文的研究对象更加普遍，研究结果的适用性更加广泛。

2 孤岛检测方法对下垂控制的适应性分析

2.1 被动孤岛检测方法的检测盲区分析

下垂控制方程式为：

(1)

式中，f*和V*分别为逆变器额定频率、额定电压幅值；P*和Q*分别为逆变器额定有功功率、无功功率；f和V分别为逆变器频率、电压幅值；P和Q分别为逆变器输出有功功率、无功功率；m和n为下垂系数。

孤岛发生后，负载吸收的有功功率和无功功率均为逆变器输出的有功功率和无功功率，即

(2)

(3)

式中，PLoad和QLoad分别为负载的有功功率、无功功率；R为负载电阻；X为负载电抗；fr为谐振频率；Qf为负载品质因数。

由式(2)可得：

V2=PR

(4)

将式(1)代入式(2)、式(3)则有：

(5)

(6)

式中，Q*=0。整理得：

(7)

(8)

由式(7)和式(8)可以看出，下垂控制的并网逆变器的孤岛检测盲区不仅与R有关，还与下垂系数m、n有关。

图1为负载R变化时的孤岛检测盲区图。可以看出，下垂控制的并网逆变器的孤岛检测盲区与负载的大小有关，R越大，则检测盲区越大，即孤岛检测盲区随着R的增大而增大。

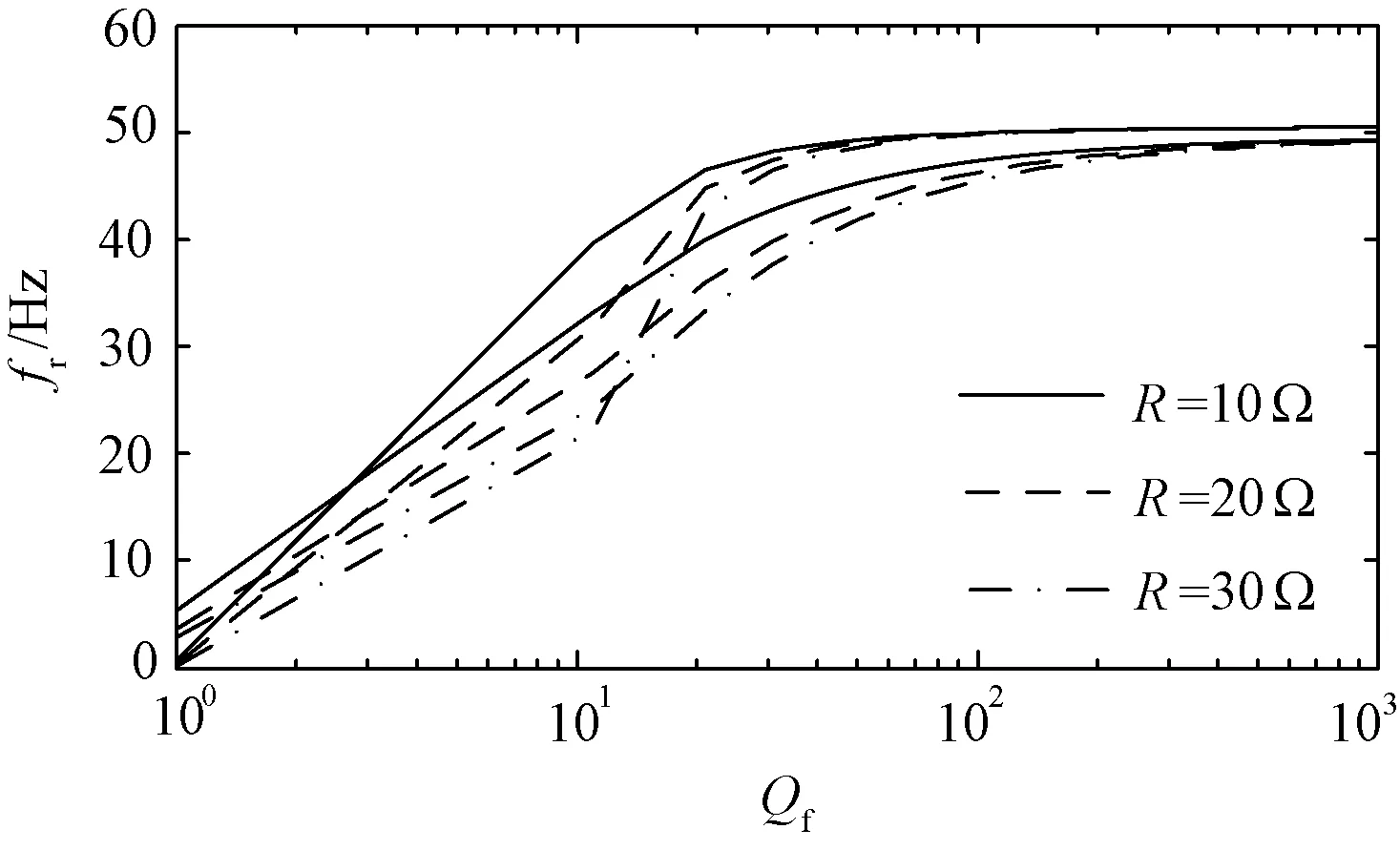
图1 R变化时的孤岛检测盲区Fig.1 Blind spot of islanding detection with changing R

图2为m变化时的孤岛检测盲区图。可以看出，下垂控制的并网逆变器的孤岛检测盲区与P-f下垂控制方程中的下垂系数m有关，下垂系数m越大，则检测盲区越小，即孤岛检测盲区随着下垂系数m的增大而减小。

图2 m变化时的孤岛检测盲区图Fig.2 Blind zone of islanding detection with changing m

图3为下垂系数n变化时的孤岛检测盲区图。可以看出，下垂控制的并网逆变器的孤岛检测盲区与Q-V下垂控制方程中的下垂系数n有关，下垂系数n越大，则检测盲区越小，即孤岛检测盲区随着下垂系数n的增大而减小。

图3 n变化时的孤岛检测盲区图Fig.3 Blind zone of islanding detection with changing n

根据以上分析可知，影响基于下垂控制并网逆变器被动孤岛检测的检测盲区的变量相较电流直接并网型逆变器要多。也就是说，下垂控制的并网逆变器成功检测出孤岛的难度要大得多。同时，由图1～图3可以看出，无论这些影响检测盲区的变量如何变化，下垂控制的并网逆变器的检测盲区相较于电流直接并网型逆变器的检测盲区要大得多，即检测出孤岛的难度要大得多。

2.2 移频法和移相法对下垂控制适应性分析

对于电流型逆变器，可以采用移频法和移相法检测孤岛[12-15]，而对于下垂控制的逆变器若采用相同的方法不能检测到孤岛的发生。下面对其进行具体分析。

移相法以主动移频法(AFDPF)为代表举例分析，主动移频法中对输出电流施加扰动θAFDPF，其中θAFDPF和相位θ可以表示为：

(9)

式中，θAFDPF为施加的扰动相位；cf0为初始截断系数；k为反馈增益；fg为电网频率；θ和ω分别为逆变器相位和角频率。

移相法以滑模法(SMS)为代表举例分析，滑模法对输出电流施加扰动θSMS，其中θSMS和θ可以表示为：

(10)

式中，θSMS为施加的扰动相位；θ0为常数；F(f-fg)为符号函数：

(11)

由式(10)、式(11)可知，无论是移频法还是移相法都是一个关于频率f的线性函数，可以统一表示为：

θ=ωt+k(f-fg)+θ0

(12)

对于下垂控制的逆变器，其输出等效为一个电压源，进行孤岛检测时不再对电流的频率进行扰动，而是对电压的频率进行扰动。加入扰动后的控制框图如图4所示，扰动后的相位表示为：

θ′=ωt+k(f-fg)+θ0

(13)

角频率ω′和频率f′表示为：

(14)

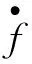
图4 下垂控制中加入扰动后的控制框图Fig.4 Block diagram of disturbance following droop control

由频率表示的加入扰动后的控制框图如图5所示。

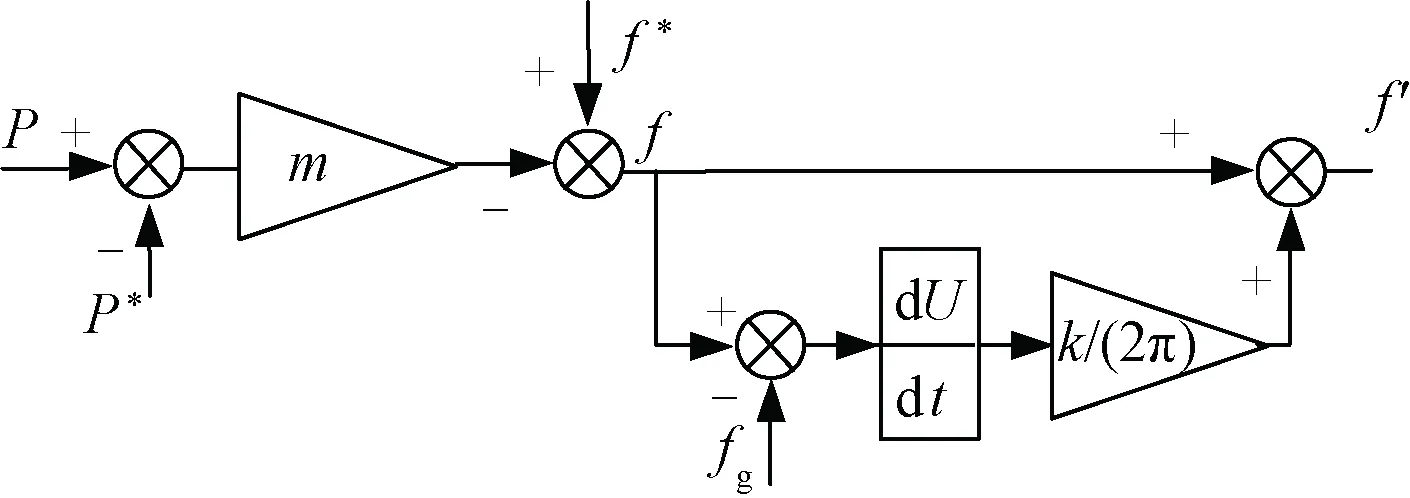
图5 由频率表示的加入扰动后的控制框图Fig.5 Block diagram of control after adding disturbance by frequency representation

将下垂控制方程式(1)带入式(14)可得：

(15)

整理后，加入扰动的频率表示为：

(16)

式中，fk为计算得到的动态频率；Pk为逆变器输出有功功率瞬时值。

ft1=f1

(17)

3 基于相位差变化率检测的改进的移相法

3.1 检测原理分析

由第2节的分析得到如下结论：将传统的移频法和移相法应用到下垂控制的并网逆变器中，孤岛发生后，逆变器的输出频率发生了一个微小的偏移，这个偏移量不会使逆变器的输出频率超出正常范围，但是，在这个频率偏移量的作用下会使得逆变器和电网之间产生相位差。然而，由于f1和fg的差值太小，所引起的相位差不会很大，如果使用这个量作为检测量，容易引起误检测。图6为采用传统移相法检测孤岛时逆变器与电网之间的相位差Δθ及其相位差的变化率|dΔθ/dt|的波形图。

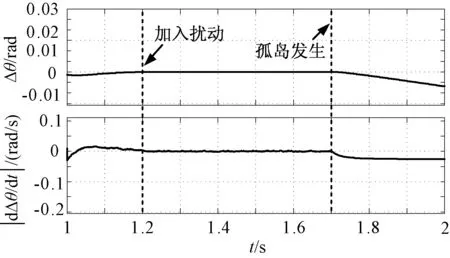
图6 传统移相法逆变器与电网相位差及其变化率Fig.6 Phase difference and rate of change of traditional phase shifted inverter

由图6可以看出，孤岛发生后逆变器和电网之间的相位差逐渐增大，但是它们的相位差的变化率非常小，仅为约0.02rad/s。若使用这种方法，无论是通过检测相位还是相位差的变化率来判断孤岛的发生都不合适，非常容易引起误检测。因此，本文提出了一种改进的移相法。

为了在下垂控制的并网逆变器中应用移频法成功检测到孤岛的发生，对于传统的方法进行改进，将传统方法中加入的扰动量f-fg改为(f-fg)/s。具体分析如下：

在逆变器输出电压的相位中加入相位扰动量，如式(18)所示，则加入扰动后的相位变为式(19)。

(18)

(19)

由于下垂控制的逆变器中输出电压的频率f是由P-f下垂方程控制产生的，而逆变器输出电压的相位θ与频率f具有如下关系：

(20)

因此式(19)可以表示为如下形式：

(21)

将扰动量k(f-fg)加到P-f下垂方程输出的频率f中，但是由于扰动量k(f-fg)中的频率f实际上是加入扰动后的量，因此，在频率f′的表达式中，扰动量k(f-fg)应表示为k(f′-fg)，则频率f′可以表示为：

(22)

即加入扰动后的下垂方程可以表示为：

f′=f*-m(P-P*)+k(f′-fg)

(23)

加入扰动后的下垂控制的控制框图如图7所示。

图7 加入扰动后下垂控制的控制框图Fig.7 Control block of sag control after disturbance

对式(23)进行整理，有：

(1-k)f′=f-kfg-m(p-p*)

(24)

即加入扰动后逆变器的控制方式依然是下垂控制，但是频率参考值变为(f*-kfg)/(1-k)，而下垂系数变为m/(1-k)。由于fg是一个维持在50Hz动态变化的量，因此在孤岛发生的时刻，(f*-kfg)/(1-k)≠f*且(f*-kfg)/(1-k)≠fg。也就是说，孤岛发生之后，系统在下垂控制的作用下，会稳定在一个非f*非fg的新的频率参考值，并且系统的下垂系数也发生变化。

令f1=(f*-kfg)/(1-k)，即孤岛发生后逆变器输出频率f最终稳定在f1不变，那么在逆变器输出频率f和电网电压频率fg的差值的作用下会引起逆变器输出电压和电网之间的相位差，当f稳定在f1不变后这个相位差会保持匀速增加，即最终它的增长率是一个不为零的恒定值。fg不是一个固定的恒量，因此在孤岛发生的瞬间，由于扰动量k(f-fg)的存在，频率f必然会发生偏移，即频率最终稳定值f1与fg的差值必然存在，也就是说孤岛发生后逆变器输出电压和电网电压之间的相位差必然存在，并且会维持线性增大，即孤岛后逆变器和电网之间的相位差|dΔθ/dt|>0，但是|dΔθ/dt|的值与扰动参数k有关。

当逆变器运行在并网模式时，若发生某些突发状况引起逆变器频率f的突变，在大电网的钳位作用下，频率f会迅速恢复到fg，逆变器和电网之间的相位差保持不变，也就是说该方法的孤岛检测量——逆变器和电网之间的相位差的变化率|dΔθ/dt|会在极短的时间内变为零。因此不能通过单独检测|dΔθ/dt|是否超过阈值δ0来判断孤岛是否发生，还应该在此基础上检测|dΔθ/dt|>δ0保持的时间是否大于t0。具体判断逻辑如下：

(1)|dΔθ/dt|与一个阈值δ0做比较。

(2)当|dΔθ/dt|>δ0时，计时器开始工作，当超过阈值t0时，发出孤岛信号。

(3)当在t0时间内|dΔθ/dt|≤δ0，此时计时器清零。

计时器的数值用tt表示，它的初始值是0。如果|dΔθ/dt|大于阈值的时间超过t0，逆变器就会发出孤岛信号，去掉加入的扰动信号，逆变器工作在孤岛运行模式。反之，如果|dΔθ/dt|在t0时间内小于等于阈值，计时器就会复位为0。阈值t0的数值依据IEEE 929-2000和IEEE 1547.1-2005的标准来设定。该方法的流程图如图8所示。

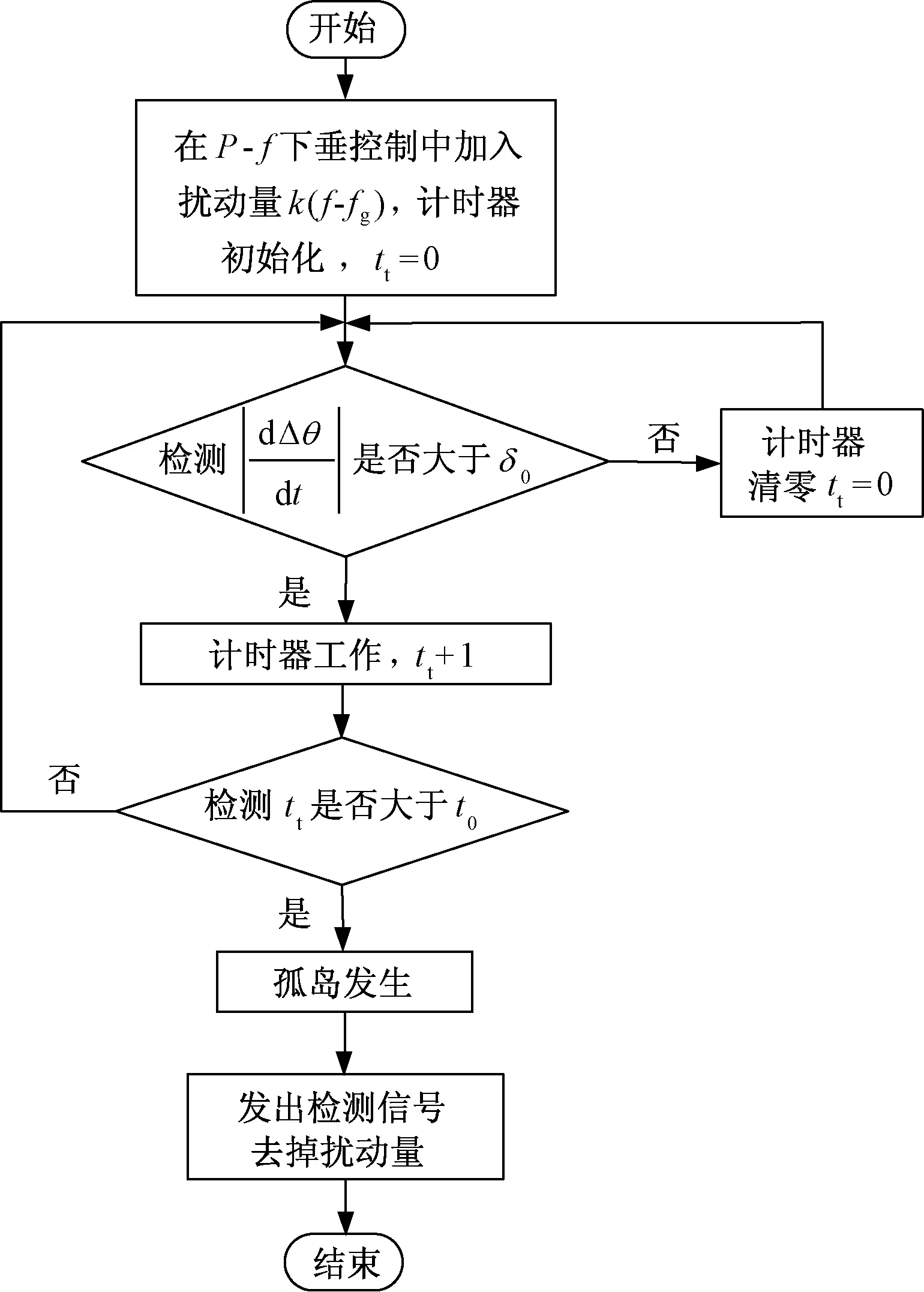
图8 基于相位差变化率检测的移频法的流程图Fig.8 Flow chart of frequency shift method based on phase difference change rate detection

3.2 基于相位差变化率检测的改进移相法参数整定

3.2.1 t0的取值

本文中的检测量t0是逆变器和电网相位差的变化率|dΔθ/dt|>δ0所维持时间的阈值，根据IEEE 929-2000和IEEE 1547.1-2005的标准，以及我国电网频率为50Hz的现实情况，当供电频率发生波动时，应该在6个周期内做出反应，停止向供电线路输电。因此本文中设置的时间阈值t0为0.12s。

3.2.2 k的取值

加入扰动后的输出电压的频率表达式为：

f(i+1)=k[f(i+1)-fg]+f*-m[P(i)-P*]

(25)

由式(25)可以看出，系数k会影响系统检测孤岛的效果以及系统的稳定性，具体如下：

(1)当k<0时，为负反馈，不能检测到孤岛。

(2)当k=0时，为传统的下垂控制。

(3)当k>0时，为正反馈，可以检测到孤岛。

虽然k>0时可以检测到孤岛的发生，但是过大的k值会导致系统的不稳定，因而需要对k的取值进行分析。

加入扰动后的传递函数为：

(26)

则系统的特征方程为：

(1-k)z=0

(27)

当k<1时，加入扰动后系统是稳定的，即频率最终会稳定在一个值保持不变。加入扰动之后的下垂曲线如图9所示。

图9 加入扰动之后的下垂曲线图Fig.9 Sag curve following disturbance

由式(3)～式(7)可以看出，由于加入扰动后的下垂系数变为m/(1-k)，为了使加入扰动后系统仍然是下垂控制，则应该使扰动系数的范围为：

k<1

(28)

这与式(27)得到的结论一致。下面对该方法的孤岛检测盲区进行分析。根据2.1节的分析可知，下垂系数m越大，则检测盲区越小。由于加入扰动后的下垂系数变为m/(1-k)，则随着扰动系数k的增大，检测盲区变小。因此为了在孤岛检测的过程中减小检测盲区，降低检测孤岛的难度，增加检测的速度，应该将扰动系数k的值设得尽量大一些；但是随着k的增大系统的稳定性降低，且当k超过一定值时，在k(f-fg)的作用下，虽然频率最终会稳定在正常范围，但是超调和调整时间会较大，因此应适当选取k的值。

4 仿真分析

逆变器运行在并网模式下，发生负载变换等情况会引起逆变器的频率波动，此时逆变器输出频率波形如图10所示。由于大电网对逆变器的钳位作用，逆变器的频率会追随电网，变为50Hz并稳定运行。在这种情况下，由于频率波动的出现，会使逆变器与电网之间出现一个相位差，但是由于频率最后会稳定在50Hz，因此这个相位差会保持不变，即最终相位差的变化率|dΔθ/dt|=0。

图10 并网模式下频率发生扰动时的频率波形图Fig.10 Frequency waveform of frequency perturbation in grid connected mode

逆变器与电网之间的相位差及其变化率如图11所示。可以看出，相位差的变化率|dΔθ/dt|在大约1.5s，即扰动发生时刻触发阈值δ0，计时器开始工作，在约0.4s后|dΔθ/dt|<δ0并最终稳定在|dΔθ/dt|=0，此时由于0.4

图11 并网运行时频率扰动后逆变器与电网之间的相位差及其变化率Fig.11 Phase difference and its rate of change between inverter and grid after frequency disturbance in grid connected operation

图12和图13为孤岛发生时的逆变器输出频率、逆变器和电网之间的相位差及其变化率和孤岛检测信号。在扰动信号的作用下，逆变器下垂控制的下垂曲线发生变化。孤岛发生后，逆变器的频率由原来的fg变为f1(49.5Hz

图12 孤岛发生时逆变器的输出频率Fig.12 Output frequency of inverter when islanding occurs

图13 孤岛发生时逆变器与电网相位差及其变化率Fig.13 Phase difference of inverter and grid and its rate of change in islanding

由图12可以看出，孤岛发生后，逆变器的输出频率迅速发生变化，变为f1=49.95Hz并保持不变。在这个频率作用下逆变器与电网之间出现相位差，并且这个相位差一直在增大，如图13所示。相位差的变化率|dΔθ/dt|在大约0.08s后触发阈值δ0，计时器开始工作，在t0内|dΔθ/dt|>δ0保持不变，此时孤岛检测信号Trip变为1，即发出孤岛信号，成功检测到孤岛的发生。

图14为孤岛发生时PCC点电压和逆变器输出电流的波形图。可以看出，采用该方法检测孤岛时不会影响逆变器的正常运行。这也是该方法的优点，可以在维持系统正常工作的情况下检测到孤岛，进而去掉扰动信号运行在孤岛模式。整个孤岛检测的过程中，系统始终正常工作，这样能够提高系统的工作效率。

图14 孤岛发生时PCC点电压和逆变器输出电流Fig.14 PCC point voltage and output current of inverter when islanding occurs

5 实验分析

图15为孤岛发生时的PCC点频率偏移量f-f0和逆变器与大电网之间的相位差的变化率的波形图。可以看出，并网运行时加入扰动后逆变器系统稳定运行，即加入的扰动对并网系统无影响；孤岛发生后PCC点频率有一个微小的变化，频率偏移量f-fg的值基本可以忽略，相位差的变化率|dΔθ/dt|没有超过阈值δ0。因此，不能通过传统的移频法/移相法在下垂控制的并网逆变器系统中检测到孤岛的发生。

图15 孤岛发生时PCC点频率偏移量f-fg和|dΔθ/dt|Fig.15 When islanding occurs PCC point frequency offset f-fg and |dΔθ/dt|

本文提出的基于相位差变化率检测的移相法属于频率扰动类孤岛检测方法。该方法在P-f下垂控制的输出频率f中加入k(f-fg)，通过在一定的时间t0内检测逆变器与大电网之间的相位差的变化率|dΔθ/dt|是否超过阈值δ0来判断是否有孤岛的发生。

图16为孤岛发生时的PCC点频率偏移量f-fg、逆变器与大电网之间的相位差的变化率、孤岛检测信号Trip。可以看出，并网运行时由于大电网的钳位作用，加入扰动后PCC点频率f不发生波动。发生孤岛后PCC点频率偏移量f-fg迅速增大并稳定在f1=50.2Hz，此时PCC点频率f仍然在允许的正常范围内。在孤岛发生的瞬间逆变器与电网之间的相位差的变化率|dΔθ/dt|迅速增大，超过设定的阈值δ0，此时，计时器开始工作。在t0时间内，相位差的变化率|dΔθ/dt|始终大于阈值δ0，符合孤岛检测的条件，认为发生孤岛，此时孤岛检测信号Trip由0变为1，发出孤岛信号，逆变器去掉扰动信号，进入孤岛运行模式。

图16 PCC点频率偏移量f-fg、|dΔθ/dt|、孤岛检测信号TripFig.16 PCC frequency offset f-fg, |dΔθ/dt|, islanding detection signal Trip

图17为孤岛检测过程中的PCC点A相电压与频率f-fg的波形图。图18为孤岛检测后的PCC点三相电压。可以看出，在孤岛检测的过程中和孤岛成功检测后逆变器的输出电压是稳定的，即本文提出的基于相位差变化率检测的移相孤岛检测方法属于非破坏性方法，使用该方法检测孤岛，可以提高逆变器系统的工作效率。由图18可以看出，加入的扰动变量并没有对逆变器的正常运行造成影响，在孤岛检测后，逆变器仍然能够正常运行，证明了该方法是一种非破坏性的孤岛检测方法。

图17 孤岛检测过程中PCC点A相电压与频率f-fg波形图Fig.17 Phase voltage and frequency f-fg waveform of PCC point during islanding detection

图18 并网运行时加入扰动后的PCC点电压Fig.18 Voltage of PCC point after disturbance in grid connected operation

6 结论

本文首先分析了下垂控制并网逆变器被动孤岛检测方法的检测盲区，然后针对移频法和移相法对于下垂控制并网逆变器的适应性进行分析，最后根据它们不适用于下垂控制并网逆变器的原因，提出了基于相位差变化率检测的改进移相法。该方法在检测孤岛的过程中具有非破坏性，能够快速、准确地检测到孤岛的发生。根据其检测原理，本文给出了扰动系数以及判断阈值的整定方法，提出了在不平衡电网情况下排除误动作的方法，并通过仿真和实验验证了理论分析的正确性。

参考文献(References)：

[1] Yang X, Song Y, Wang G, et al. A comprehensive review on the development of sustainable energy strategy and implementation in China[J]. IEEE Transactions on Sustainable Energy, 2010, 1(2): 57-65.

[2] IEEE Std 929-2000, IEEE recommended practice for utility interface of photovoltaic (PV) system[S].

[3] 张有兵，穆淼婕，翁国庆(Zhang Youbing, Mu Miaojie, Weng Guoqing). 分布式发电系统的孤岛检测方法研究(Islanding detection method for distributed generation system)[J]. 电力系统保护与控制(Power System Protection and Control)，2011，39(6)：140-146.

[4] Mahat P, Chen Z, Bak-Jensen B. Review of islanding detection methods for distributed generation[A]. Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies[C]. 2008. 2743-2748.

[5] 张纯江，郭忠南，孟惠英，等(Zhang Chunjiang, Guo Zhongnan, Meng Huiying, et al.). 主动电流扰动法在并网发电系统孤岛检测中的应用(Application of active current perturbation method in islanding detection of grid connected power generation system)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2007，22(7)：176-180.

[6] 张岚，殷桂梁，韩郁，等(Zhang Lan, Yin Guiliang, Han Yu, et al.). 基于无功微扰/频率偏差相关度的光伏发电系统孤岛检测方法(Islanding detection method of photovoltaic system based on reactive power perturbation/frequency deviation correlation)[J]. 南方电网技术(Southern Power System Technology)，2010，4(S1)：130-133.

[7] 阚加荣，罗运虎，谢少军，等(Kan Jiarong, Luo Yunhu, Xie Shaojun, et al.). 基于下垂特性锁相环的反孤岛性能分析(Performance analysis of anti islanding based on droop characteristics of phase locked loop)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2013，28(4)：165-170.

[8] 陈江艳(Chen Jiangyan). 电压、频率正反馈孤岛检测法的研究(Study on islanding detection method of voltage and frequency positive feedback)[J]. 河南科技(Henan Science and Technology)，2013, (2)：26-27.

[9] Lissandron S, Sgarbossa R, Dalla Santa L, et al. Impact of non-simultaneous P/f and Q/V grid code requirements on PV inverters on unintentional islanding operation in distribution network[A]. 2005 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems[C]. 2015. 1-7.

[10] 阚加荣，谢少军，姚志垒，等(Kan Jiarong, Xie Shaojun, Yao Zhilei, et al.). 低压微电网中并网逆变器主动移频式孤岛检测技术(Active frequency shift islanding detection technique for grid connected inverters in low voltage microgrid)[J]. 电力系统自动化(Automation of Electric Power Systems)，2012，36(7)：33-37.

[11] 贺超，王冕，陈国柱(He Chao, Wang Mian, Chen Guozhu). 基于下垂控制的孤岛检测方法及其改进策略(Islanding detection method based on droop control and its improvement strategy)[J]. 电力自动化设备(Electric Power Automation Equipment)，2015，35(6)：87-92.

[12] John V, Ye Z, Kolwalkar A. Investigation of anti-islanding protection of power converter based distributed generators using frequency domain analysis[J]. IEEE Transactions on Power Electronics, 2003, 19(5):1177-1183.

[13] Yin J, Chang L, Diduch C. A new adaptive logic phase-shift algorithm for anti-islanding protections in inverter-based DG systems[A]. IEEE 36th Power Electronics Specialists Conference, PESC’05[C]. 2005. 2482-2486.

[14] 刘方锐，康勇，张宇，等(Liu Fangrui, Kang Yong, Zhang Yu, et al.). 带正反馈的主动移频孤岛检测法的参数优化(Parameter optimization of active frequency shift islanding detection with positive feedback)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2008，27(3)：22-25.

[15] 刘方锐，康勇，张宇(Liu Fangrui, Kang Yong, Zhang Yu). 光伏并网逆变器的孤岛检测技术(Islanding detection technique for photovoltaic grid connected inverters)[J]. 电力科学与技术学报(Journal of Electric Power Science and Technology)，2009，24(1)：8-11.