在数学课堂中提升学生阅读理解能力的策略初探

卢巧萍

（广东省广州市荔湾区新东小学）

结合多年的教学实践发现，每次的测试评讲后，学生所写的反思无外乎写失分的原因是“我审题不够仔细；我没有理解题意，我粗心大意”。这样的解释从表面上看似乎合情合理，但我们更应该追根溯源，进一步剖析是什么原因导致学生分析问题、收集筛选有用的信息、解决问题的能力不足，又是什么原因让学生题目都没有读懂。我们所教的班级，一定会有一些学习困难生，对于教师来说，教学工作中的很多时间是在辅差，一线教师的精力大部分花在对这些学习困难生的辅导上。到底是什么原因造成了学生学习上的困难呢？我们认为，原因就是：由于基础知识薄弱，导致阅读有困难，理解能力不足，综合运用能力差。但是通过教学以来对自己任教班级学生的作业、单元测验进行跟踪分析，发现这些问题存在的原因不能这么简单地分类，还有更加细化、更加深层次的原因。因此，我认为根本的原因就是学生对数学阅读理解有困难。由于不能把符号或图形与文字进行互译，就造成理解不了题目中文字所表达的意思，从而造成不会审题，不能理解。所以，只有当学生具有较强的阅读理解能力时，才能达到准确理解题意的效果。为此，在学习数学时，教师要有培养学生数学阅读习惯的意识，不断提高学生理解能力，这一点是非常重要的。

一、对数学课本中的公式及概念阅读方法指导策略的研究

“授人以鱼，不如授人以渔。”学生虽然具备一定的语文阅读基础，但是由于个体差异，理解能力的高低也就参差不齐，加上数学理解不等同于语文理解，如何让学生准确理解数学课本中的公式及概念，需要教给学生有效的学习数学的方法。阅读是提升学生学习效率的有效途径，反复阅读、精准阅读能够不断提升学生的数学思维能力。对于数学文本中呈现出来的概念、公式等教学内容，教师从学生理解角度和难度出发作引导性指导，提升学生数学阅读能力，这样才能从根源上解决学生遇到的数学问题。如果学生没有读懂教材，自己不会阅读，教师的课讲得再好，学生还是没有达到真正掌握知识的效果。

如“方程的意义”的教学，可以让学生观察黑板上书写的式子，根据式子的特点按要求进行分类。

按照两种分类方法把对应的式子填入下列的表格里：

含有未知数 不含有未知数等式不等式

引导学生根据上面表格的信息，概括出符合方程的条件。第一是有字母的，第二是有等号的。接着还要让学生在书本上圈出“未知数”及“等式”，读的时候这些重点词要加重语气来读。

教授平面图形面积计算公式推导时，不但要让学生动手实践，更要让学生通过理解书本内容准确寻找计算的各个条件。例如：“下图中的平行四边形被分成两个大小相同的三角形，它们的面积都是180平方米，求平行四边形的周长。”

学生首先要掌握“平行四边形的周长”概念，理解“围绕平行四边形一周所有线段的和”就是“平行四边形的周长”这个知识点，从而学生发现了这两个三角形的底就是这个平行四边形的周长，还要根据平行四边形的特征“对边相等且平行”，就可以计算出结果，就是：180×2÷18=20（厘米），180×2÷22.5=16（厘米），20×2+16×2=72（厘米）。

二、对计算题阅读方法指导的策略研究

教授四则运算，关键点是要让学生理解算理。为此，计算法则和运算顺序学生必须理解清楚，教师必须引导到位，这样才能正确算出得数。但在实际的教学中，个别学生由于对运算定律及顺序一知半解，理解不透彻，在一些特殊数据的刺激下，被表象的“容易算”所误导。如 1.02－1.02÷3=0，2.5×4÷2.5×4=1 等。在练习时，教师要引导学生首先读清楚题目的数字特点和运算顺序，二要用尺子划出先算的部分，三是想一想可以运用哪个运算定律使这道题可以计算简便，四是要仔细计算，五是在计算过程中一步一回头检查有没有搬字过纸时抄错数字，导致计算错误。

如，在学习四则混合运算中，怎样算简便就怎样算的教学里，该单元学生作业反馈效果不理想。学生不知道什么情况下运用乘法结合律，什么情况下运用乘法分配律，教师也会疑惑：运算定律学生都已背得滚瓜烂熟，但在实际计算中为什么还是不能正确灵活运用？究其原因就是学生没有认真读题，不能发现题中的数字特点，只会背定律，不能判断能不能运用运算定律，如果能，又可以运用哪个；还有的就是对计算中的定律不清晰，没有真正理解算理，导致计算错误。为了让学生能在四则混合运算中灵活运用运算定律，教师可以根据题目的数字特点把这些运算定律编成容易记忆、朗朗上口的语句。如：计算0.9×2.5，编成的顺口溜是加减在中间，乘除在两边，有可能是乘法分配律，把除号转化乘号，除数转化它的倒数，再把相同的数抽出来做因数，其余的数做加数或减数。又如，35.97－（4.86+5.97）14－7.32－2.68，减除在前面，无论加（ ）或拆（ ），里面都要变号。又如12.5×8÷12.5×8，编成的顺口溜是同级运算，数字带着前面的符号搬家。

三、对解决实际问题阅读方法指导的策略研究

对解决实际问题阅读理解方法指导的策略研究长期以来都是小学数学教学的重难点。学生最头疼的是做解决问题，单元检测或期末考查时不少学生在解决问题这部分失分最厉害。原因就是这些学生没有掌握读题的方法，读不懂题目，没有准确梳理出题中的等量关系。为此，教师要从学生角度出发，预设学生理解题目的瓶颈，有效指导学生抓关键词理解，逐渐养成阅读思维的条理性和高效性。

有时候在一些解决问题的题目里，由于文字多、信息多，给学生的阅读造成了一定的影响。如：你知道你家这个季度的用水量吗？现在家里水表上的所显示数字是表示自我们的水表安装以来的用水总数量，用现在水表读数减去前一次的读数，就是我们家这次的用水量了。

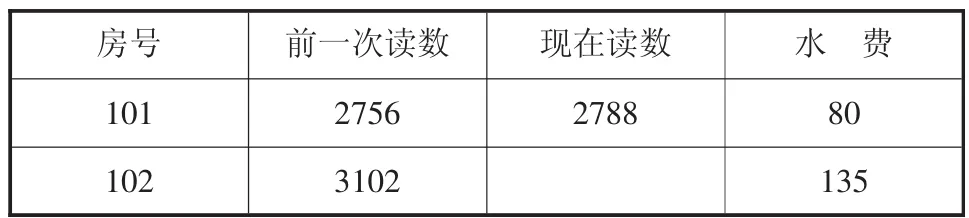
1号宿舍4～6月份水费收取表单价：2.8 元/吨

102室本次的读数是多少？

学生一看到文字多、篇幅长、信息量大的题目，就像是在做一篇语文阅读理解题，许多学生已经是望而却步，不愿意继续读下去，更谈不上是理解了。其实，仔细阅读完题目后就会发现这么多的文字里有用的信息只有那么一两个，只要学生静下心来阅读，抓住关键词，就可以顺利解答了。这道题只要抓住“两次读数的差就是本次用水吨数”和102室的信息及单价，就可以写出数量关系式“单价×两次读数差=总价，列出的方程是2.5×（x－3102）=135”。101室的信息都是多余的。

在一次单元检测中有一道判断题“16比x的3倍少5。列方程是3x－16=5。（ ）”。有40%的学生判断错误。这类型的判断题文字不多，也给学生造成一个假象，就是按文字的叙述列方程是“16－3x=5”。做文字这么少的而又出现在判断题中，给学生一个心理暗示，是简单且要快速判断的，因此学生思考的时间不长，没有真正地读、理解题意就进行判断了。所谓“读书百遍，其义自见”，做这些文字题时，更需要学生仔细反复地读，分析题中的数量关系，用尺子画出x的3倍就是3x，然后把题目读“薄”，缩句为“16比3x少5”，这样这道题的数量关系就简明多了。

四、图形题阅读方法策略的研究

图形计算题在各年级的教材中占有很大的比重。有部分学生不会看课本中出现的情境图，表格图、线段图、几何图形看不懂，就无法进行正确解答。这部分教学内容需要教师组织学生有序看图，读懂图形，理解图中的一些数量关系，使学生使用数学语言正确、完整地进行表述。

如，图中是两个大小相等的三角形重合一起，你能求出图中涂色部分的面积吗？

教学这道题时，教师让学生提炼出条件中有用的信息，转化为正确的数学语言完整地表述出题意。从第一个信息条件中就可以得出这两个三角形的面积是一样的。根据这个等量关系就可以写出一个等量关系式，图中的△EAD面积+阴影面积=△EAD面积+梯形ABCD面积。根据等式的性质，这个等式的两边同时减△EAD面积，就得出以下等式：

阴影面积+△EAD面积=梯形ABCD面积+△EAD面积

阴影面积+△EAD面积－△EAD面积=梯形ABCD面积+△EAD面积－△EAD面积

阴影面积=梯形ABCD面积

就把求图中阴影面积转化为求梯形ABCD的面积。根据梯形的面积计算公式

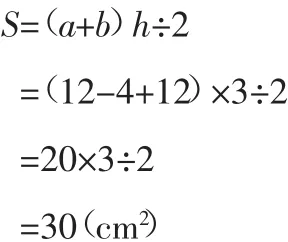
学生的数学阅读理解能力能否得到提升，贵在每一节数学课堂上教师的悉心引导、耐心指导。教师教给方法，学生方能学以致用，每课有得，良好的阅读习惯和思维习惯就能逐渐养成。

参考文献：

［1］石正伟.小学数学课堂中体现“小老师”的价值实现教育信息化［J］.中小学电教（下半月），2017（2）.

［2］汪青.微课资源在小学数学课堂教学中的应用探讨［J］.小学科学（教师版），2017（4）.