一种离散反向学习的萤火虫特征选择算法

徐华丽，郁书好，左旭坤，陈家俊

(皖西学院 电子与信息工程学院，安徽 六安 237012)

特征选择(feature selection)作为一种数据预处理手段近年来广泛应用到各行各业中，例如社会网络、入侵检测、生物信息、图像分析和自然语言处理等。在大规模数据集中，通常存在着大量冗余和无关特征，特征选择的目的在于去掉初始集合中的冗余特征，选择和分类目标相关的特征。特征选择是通过一个特定的评估函数来评价特征或特征组合，进而从原始特征集合中选择出一个维度更低的特征子集[1]。该子集能够在数据挖掘和机器学习任务中提供与原集合近似或更好的表现。因此，为了能够从大量高维小样本的数据中获取有用的信息，利用特征选择对数据降维成为了处理这类问题的一个有效方法。

目前，关于特征选择的算法研究依据特征子集性能评价准则可分为3类：过滤法，封装法和嵌入法[2]。过滤法采用的评价标准与后续的学习算法无关，依据特征对分类贡献的大小定义其重要程度，选择重要的特征构成特征子集，目前用得最多的过滤法是相关测量法、类间和类内距离测量法、信息熵法、t检验以及ReliefF等。过滤法通常能够很快地排除一部分非关键性的噪声特征，缩小优化特征子集的搜索范围，但是并不能保证选择出一个规模较小的优化特征子集。封装法的算法与分类器相关联，依据不同的特征子集的分类性能评价特征子集中的特征，计算复杂度相对较高，在处理大规模数据时能从初始特征集合获取某个特征子集。嵌入法是指特征选择算法嵌入到分类算法中，特征选择和训练同时进行，不需要将数据集分为训练集和测试集。封装法相比过滤法，其所选的优化特征子集的规模相对要小一些。因此，该方法是特征选择研究领域的热点。特征选择问题本质上是NP的组合优化问题，可采用非全局最优目标搜索方法求解这类问题，因此近年来出现了一些用于解决这类问题的元启发式方法。如文献[3]提出了用决策树来进行特征选择的方法，用遗传算法来寻找使得决策树分类错误率最小的一组特征子集。文献[4]使用正态极大似然模型来进行特征选择和分类，得出了较好的实验结果。文献[5]用遗传算法结合人工神经网络得出了较好的实验结果，文献[6]利用支持向量机（SVM）作为分类器，所选择的优化特征子集的分类准确率比神经网络、决策树、k近邻分类算法的有了更进一步的提高。文献[7]提出了一种混合遗传算法的特征选择算法、文献[8]提出了一种蚁群优化算法优化支持向量机的核参数的特征选择算法、文献[9-10]将粒子群算法优化运用到特征选择算法中取得了很好的分类效果。萤火虫算法(firefly algorithm，FA)[11]由剑桥大学Yang于2009年提出，作为最新的群智能优化算法之一，该算法已经被证明比PSO（particle swarm optimization）和GA（genetic algorithm）具有更好的收敛速度和寻优精度，且易于工程实现，目前已被成功应用到多种领域[12-15]。因此本文使用萤火虫算法进行特征选择。

特征选择的实质是离散组合优化问题，本文提出了一种基于近邻信息的离散反向学习萤火虫特征选择算法（neighborhood information and discrete opposition firefly algorithm for feature selection，NOFAFS）。主要贡献如下：（ⅰ）针对萤火虫算法对初始解质量的依赖，在算法初始化阶段，引入二进制编码和反向学习产生初始解，增加获得最优解的机会；（ⅱ）为了避免在离散化处理数据时丢失了一些重要信息，避免算法种群多样性的丢失，在搜索过程中运用反向学习策略，使其跳出局部最优，增加粒子的多样性，提高萤火虫找到最优值的概率；（ⅲ）将该特征选择算法获得的特征子集应用到UCI标准数据集中进行测试，通过实验验证了所提方法的有效性。

1 相关工作

1.1 萤火虫算法描述

在基本萤火虫优化算法中，初始时刻，萤火虫随机分布在整个搜索空间，萤火虫通过发出亮光来吸引其他萤火虫个体，从而达到移动。其移动过程遵循三个基本假设：

（H1）所有萤火虫不区分性别，会被吸引到荧光亮度更高的萤火虫那边去；

（H2）萤火虫的吸引力和亮度成正比，其中，低亮度的萤火虫会被高亮度的萤火虫吸引并向其移动，亮度是随着距离的增加而减少；

（H3）萤火虫的亮度由其适应值函数决定。

在基本萤火虫优化算法中，亮度和吸引度是其重要的两个参数，亮度体现了萤火虫所处位置的优劣并决定了其移动的方向，吸引度决定了萤火虫移动的距离，亮度和吸引度不断变化更新，从而实现目标优化。

萤火虫i对萤火虫j的相对荧光亮度为

其中，I0为萤火虫的最大荧光亮度，与目标函数值相关，目标函数值越大，亮度越高，γ为光吸收系数，荧光亮度会随着距离的增加逐渐变弱，rij为萤火虫i和j间欧氏距离。

萤火虫的吸引度为

其中，β0为rij=0时的吸引度。

萤火虫i被吸引向萤火虫j移动的位置更新公式如下式:

其中，xi是萤火虫的当前位置，α∈[0,1]为随机步长，rand∈[0,1]表示随机数。

1.2 反向学习

反向学习策略是2005年提出的智能学习策略，学者们已经证明该策略是一种有效的提高各种优化问题效率的方法[16]。反向学习策略主要是当检测到种群历史最优位置在一定迭代次数内时未更新，算法陷入停滞，或将当前历史最差位置萤火虫产生反向解，并将反向位置萤火虫与当前萤火虫一起参与竞争，优秀萤火虫个体进入下一代。

设存在实数x∈[m,n]，则x的反向数定义为：

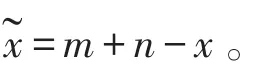
设在R上存在d维空间上点x=（x1，x2,…xd)，且xi∈[mi,nj]，i∈{1,2,…d}，则其反向数可定义为：

如果f()≥f(x)，则用反向解代替初始解x。

2 基于离散反向学习的萤火虫特征选择算法

2.1 离散萤火虫编码方案

针对特征选择问题，本文采用离散型萤火虫优化算法，其解的具体构造如下：

初始化一个概率向量矩阵X=（xi1,xi2,...,xid），萤火虫个体i在第d维的位置用xid表示，i表示萤火虫群体的规模，d表示一个数据集所包含的特征属性的个数，xid在解向量中所处的位置与数据集中的序号一一对应，xid∈[0,1]表示数据集中第d个属性，为特征被选中的概率，对于任一个萤火虫个体xi，其编码方案由下式决定：

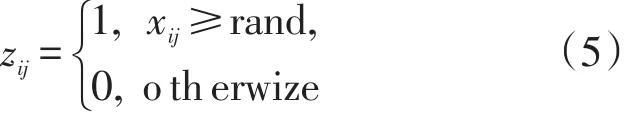
zij=1表示第j个特征被选中到特征子集zij中。特征子集zij的值通常只能取0或1，0表示该属性未被选中，1表示该属性被选中。例如，一个可行解表示的一个候选子集如：x=(0.7,0.3,0.6,0.8,0.4,0.2,0.3,0.9)，当rand=0.5时，表示原始数据集中的序号为第1,3,4,8的属性被选择，构成一个候选子集。因此，特征选择问题即转变为离散变量的优化问题。

2.2 反向学习的初始化策略

萤火虫的初始解构造策略直接影响到算法的收敛速度和解的质量，在经典的萤火虫优化算法中，初始解一般都是随机生成或者混沌产生的，本文采用基于反向学习的初始构造策略，随机初始一个解，并应用式（4）产生反向解，同时搜索当前解和反向解，选择两者中适应值较好的解作为初始解，从而提高初始解的质量。

2.3 适应值函数的构造

特征选择的目的在于所选择特征子集具有很强的分类能力，因此，在特征选择时，考虑特征子集形成的分类器的分类精度，是非常有必要的。为了计算萤火虫对应的特征子集形成的分类器的精度，本文采用留一交叉验证法，即将含有K个数据的数据集，以每个数据分别作为一次验证集，其他K-1个数据作为训练集。假设以第i个数据为验证集，则将第i个数据以外的其他K-1个数据作为训练集，对萤火虫所对应的特征子集形成的分类器训练，从而得到一个分类模型，然后利用第i个数据测试分类模型的性能，如果分类模型预测出的类别正确，则Si=1，否则，Si=0。可将结果统一表示为Si(x)，则对于K个数据，萤火虫x对应的特征子集形成的分类器精度可表示为：

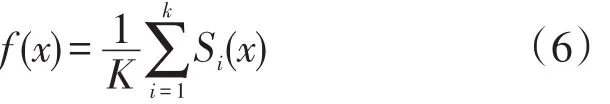
2.4 反向学习机制

群智能算法的一个关键问题是如何在保持种群多样性和提高算法收敛速度之间寻求一种平衡。因为随着算法的不断迭代，算法容易出现早熟收敛现象，因此提出了NOFAFS，即在算法搜索过程中，以加强种群历史最优个体的局部开采能力为前提，利用多个粒子的反向学习能力，保持种群多样性。具体策略如下：（ⅰ）当检测到种群最优位置在一定的迭代步数内没有更新时，则算法可能陷入停滞，可将当前种群中10%的萤火虫进行反向学习，其他90%的学习方式不变；（ⅱ）为了能够使这些最差萤火虫能够快速逃离当前局部最优，并且让它们尽可能地不同，应选择两两之间欧式距离大于预设的一个排异半径r的萤火虫个体。

2.5 算法步骤

算法步骤如图1所示。

3 实验与结果分析

3.1 实验环境及参数设置

本文代码工具采用Matlab2014a，编译运行的机器配置如下：64位windows 10操作系统，CPU 2.3 GHz i5-4200U、内存8 GB。本文实验中参数设置如下：α=0.2,β0=1,γ=1萤火虫个数初始化为25。

3.2 实验结果分析

为验证该算法的有效性，采用UCI数据集（http://archive.ics.uci.edu/ml/）中的4个不同数据集（见表1）进行测试，并应用两种不同方法进行对比实验，用于比较基本萤火虫算法进行特征选择（firefly algorithm for feature selection，FAFS）和本文算法NOFAFS在分类方面的效果，分别用来测试特征选择后的特征数量和由选择出的特征子集进行分类得出的分类精度。

表2给出了上述4个不同数据集分别应用两种不同的算法后选择的特征子集的个数，结果显示不同算法得到的特征子集的数量是不同的，表3给出了两种算法所选择的特征子集是不同的，以Heart disease数据集为例，FAFS选出的特征子集为 13,12,8,3,10,7,9,11,1,4,2,5,6，而 NOFAFS选出的特征子集为12,3,11,13,7,4,9。

在实验中，为比较特征选择后的特征子集的分类能力，选取LSVM、CART两种不同分类器并利用十字交叉验证的方式评价特征子集的优劣，其中支持向量机使用线性支持向量机。

图1 NOFAFS算法

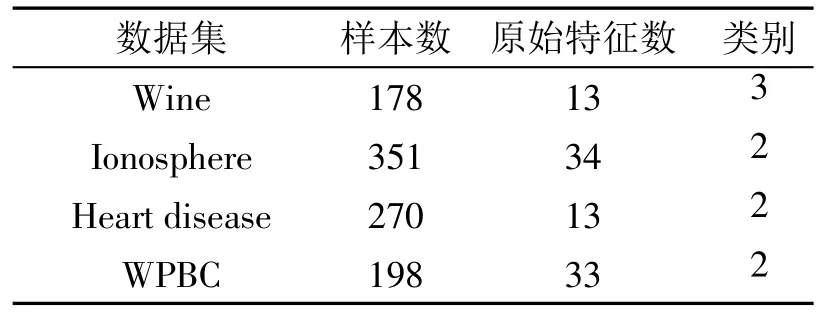
表1 实验数据描述及不同算法选择的特征数量

表2 FAFS和NOFAFS的所选择特征子集比较

为了进一步说明本文算法的有效性，同时选取了经典PSO算法进行特征选择(PSOFS)比较实验。表3分别给出了4种数据集在不同的分类器下的评价各算法的分类精度。从表中可以看出，大多数情况下，在经过特征选择后，算法能维持或增加了分类精确性。例如数据集Wine共有13个特征，选择FAFS算法，特征子集数量减少2，分类器分类精度保持不变；利用NOFAFS后，利用LSVM算法分类器特征子集数量减少为10，分类精度较原始特征集有0.66的提高，较PSOFS提升了1.1。而数据集WPBC在原始特征数为33的情况下，经特征选择后特征子集数量减为2的条件下，仍然能保持较高分类精度，仅减少了1.41个百分点。而在利用CART分类器的情况下，特征子集数量大大减少的同时分类精确性反而有所提高。例如对于lonosphere数据集，选用FAFS特征子集数量由22减少至9，而分类精度达到98.00，比原始数据集获得的精度91.17有了6.83的提升。从表中可见，选用NOFAFS特征子集数量为10，比FAFS多1，而分类精度为98.58，相比FAFS有了0.58个百分点的提升，相比PSOFS有了2.0的提升。由此说明，并不是特征子集数量越多分类精确性越高，删除冗余或不相关特征有时反而更能提高分类算法的分类精确性。综合以上分析，可以看出，NOFAFS较FAFS算法在分类精确性和特征数量上都有了明显提升，较PSOFS也有了明显提升，说明本文应用反向学习策略初始化和针对早熟收敛现象的反向学习策略，能够引导萤火虫快速逃离局部最优，算法性能获得明显提升。

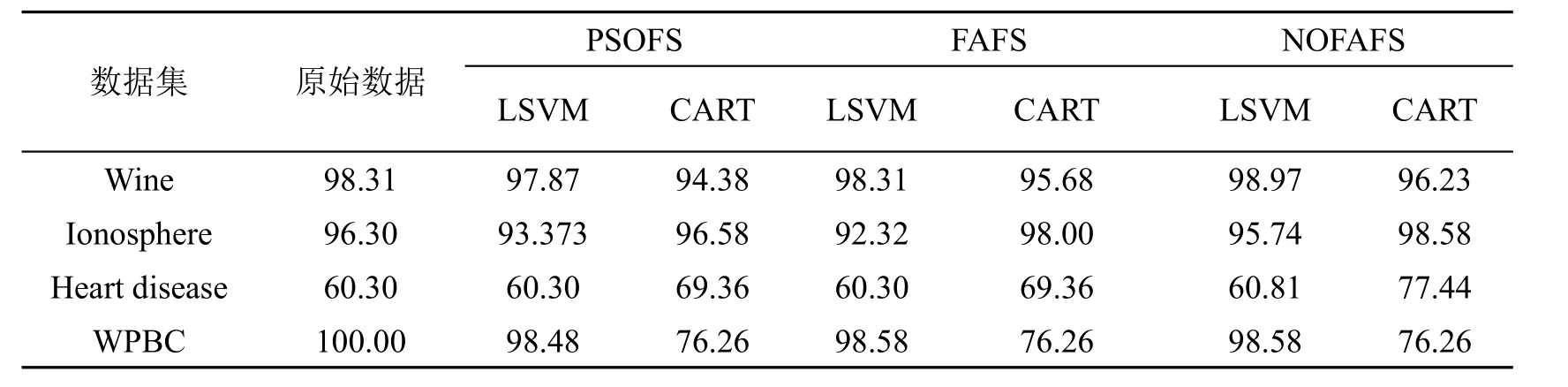
表3 不同特征选择算法在不同分类器下的分类精度比较（LSVM算法和CART分类算法）

4 小结

大数据呈现出数据量巨大、数据维度高、价值密度低、增长速度快等特点，特征选择在降低数据维度、在数据分类中起着至关重要的作用。本文提出了一种新的离散反向学习的萤火虫优化特征选择算法，利用反向学习机制使得萤火虫能快速找到最优特征子集。实验结果表明，本文所用方法简单有效，在UCI数据集上测试，能够获得较好的分类精确度。对于实际应用过程中，如何提升算法的执行效率是下一步需要仔细研究的问题。

参考文献：

[1]董红斌，腾旭阳，杨 雪.一种基于关联度信息熵度量的特征选择方法[J].计算机研究与发展，2016，53（8）：1684-1695.

[2]Liu H,Yu L.Toward integrating feature selection algorithms for classification and clustering[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(4):491-502.

[3]Hsu W H.Genetic wrappers for feature selection in decision tree induction and variable ordering in Bayesian network structure learning[J].Information Sciences,2004,163(1):103-122.

[4]Tabus I,Astola J.On the use of MDL principle in gene expression prediction[J].EURASIP Journal on Applied Signal Processing,2001,2001(1):297-303.

[5]Li L,Weinberg C R,Darden T A,et al.Gene selection for sample classification based on gene expression data:study of sensitivity to choice of parameters of the GA/KNN method[J].Bioinformatics,2001,17(12):1131-1142.

[6]Shima K,Todoriki M,Suzuki A.SVM-based feature selection of latent semantic features[J].Pattern Recognition Letters,2004,25(9):1051-1057.

[7]Oh I S,Lee J S,Moon B R.Hybrid genetic algorithms for feature selection[J].IEEE Transactions on pattern analysis and machine intelligence,2004,26(11):1424-1437.

[8]Huang C L.ACO-based hybrid classification system with feature subset selection and model parameters optimization[J].Neurocomputing,2009,73(1):438-448.

[9]Xue Bing,Zhang Meng-jie,Browne W N.Particle swarm optimisation for feature selection in classification:Novel initialisation and updating mechanisms[J].Applied Soft Computing,2014,18(4):261-276.

[10]Chuang LY,Tsai S W,Yang C H.Improved binary particle swarm optimization using catfish effect for feature selection[J].Expert Systems with Applications,2011,38(10):12699-12707.

[11]Yang X S.Firefly algorithm,stochastic test functions and design optimisation[J].International Journal of Bio-Inspired Computation,2010,2(2):78-84.

[12]Jati G.Evolutionary discrete firefly algorithm for travelling salesman problem[J].Adaptive and intelligent systems,2011:393-403.

[13]Khadwilard A,Chansombat S,Thepphakorn T,et al.Application of firefly algorithm and its parameter setting for job shop scheduling[J].J.Ind.Technol,2012,8(1).

[14]Abedinia O,Amjady N,Naderi M S.Multi-objective environmental/economic dispatch using firefly technique[C]//Environmentand ElectricalEngineering(EEEIC),2012 11th International Conference on.IEEE,2012:461-466.

[15]Long N C,Meesad P,Unger H.A highly accurate firefly based algorithm for heart disease prediction[J].Expert Systems with Applications,2015,42(21):8221-8231.

[16]Tizhoosh H R.Opposition-based learning:a new scheme for machine intelligence[C]//Computational intelligence for modelling,control and automation,2005 and international conference on intelligent agents,web technologies and internet commerce,international conference on IEEE,2005,1:695-701.