一类风险模型的破产概率的渐近性分析

严 钧，杨泽伟

（扬州大学 数学科学学院，江苏 扬州 225002）

破产概率一直保险精算领域研究的热点问题[1-7]。本文分析影响破产概率的影响因素，并且给出破产概率的一种渐近行为。假设赔付随机变量X1,X2...Xn...独立同分布，则保险公司的盈余过程可以表示为

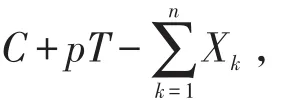
其中C＞0为保险公司的初始资本，p＞0为保险公司的费率，n表示到T为止发生的索赔次数。

表示T时刻保险公司破产的概率。记μ=E(X1)，保险公司一般要求=nμ不妨设，其中δ＞0称为安全负载。

1 破产概率的影响因素分析

由中心极限定理可知，如果Var(X1)＜+∞，则

即

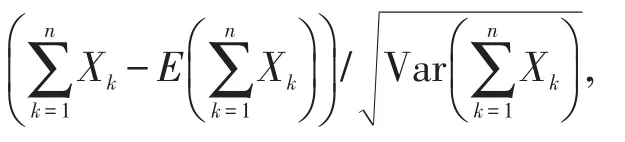
依分布收敛到标准正态分布，所以当n充分大时，（近似服从）。

由于正态分布的线性函数仍然是正态分布，所以有

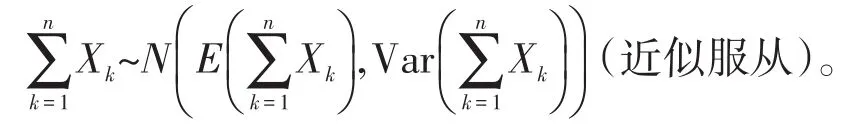
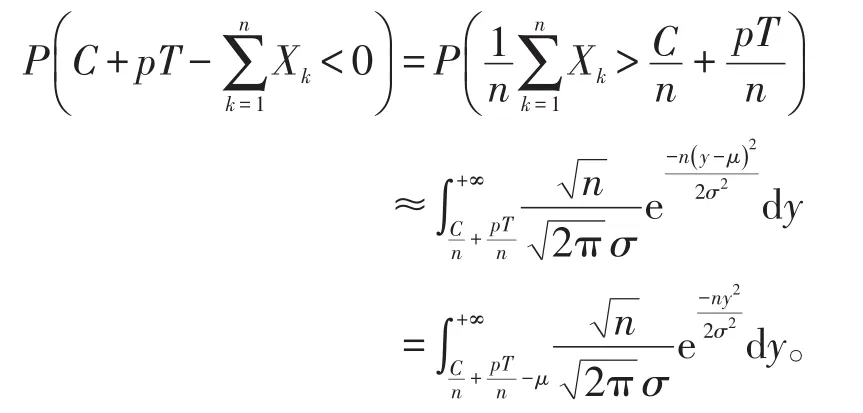
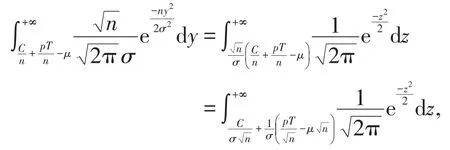
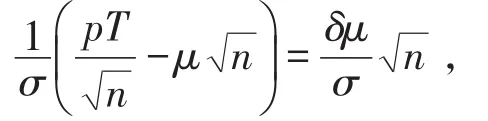
所以当n充分大时，

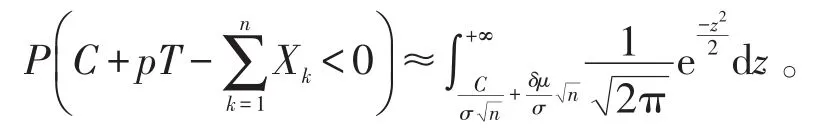
以下分析的是破产概率的影响因素：

对固定的n，

(1)初始资本C越大，破产概率越小。可见初始资本是衡量保险公司实力的重要标准，所以对一个保险公司来说，资本越雄厚，实力越强，其抵御风险的能力也就越强。

(2)安全负载δ越大，破产概率越小。另一方面，pT=(1+δ)nμ，所以安全负载越大，保险费率越高，也就是保险越贵。

(3)σ越小，破产概率越小，σ所刻画的是损失变量X1,X2,…Xn,…的波动程度。损失波动程度越小，面临破产的概率就越小，这符合直观认识，即赔付量越稳定，风险越小。例如，如果保险公式遇到巨额索赔，可能直接导致其破产。

2 破产概率的渐近行为

为了证明定理1，需要下面的引理。

对上式两边同时取对数并除以n，可得到

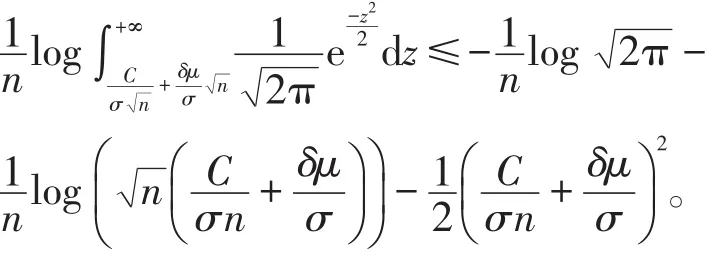
另一方面，再由引理1，有

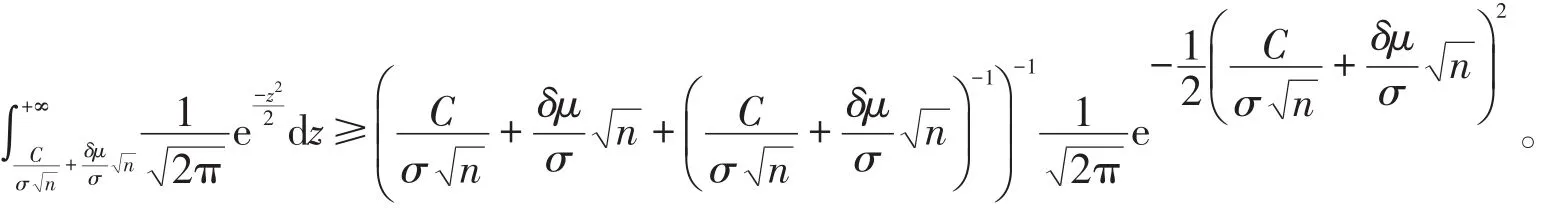
类似地，有下式

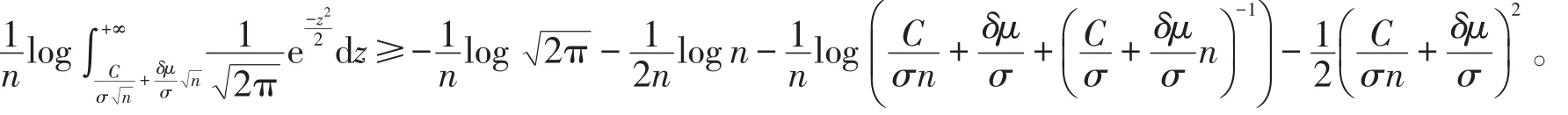
所以，

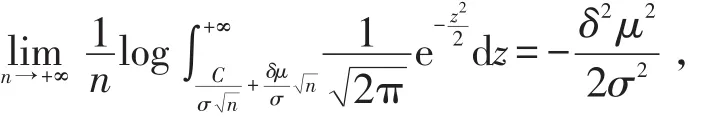
也就是说，当n充分大时，

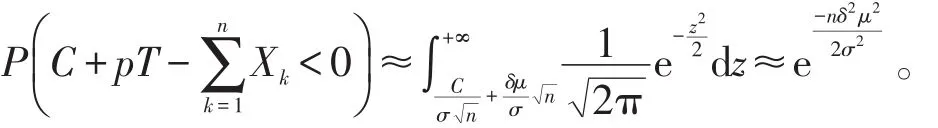
3 小结

本文运用中心极限定理分析一类风险模型的破产概率随初始资本、安全负载和索赔的方差变化情况，给出了破产概率衰减到零的速度，这些结果可以指导金融保险公司规避风险。

参考文献：

[1]Landriault D,Li B,Loke S H,et al.A note on the convexity of ruin probabilities[J].Insurance:Mathematics and Economics,2017,74(1):1-6.

[2]Gajek L,Rudź M.A generalization of Gerber’s inequality for ruin probabilities in risk-switching models[J].Statistics&Probability Letters,2017,129(4):236-240.

[3]Chen Y Q,Yuan Z Y.A revisit to ruin probabilities in the presence of heavy-tailed insurance and financial risks[J].Insurance:Mathematics and Economics,2017,73(1):75-81.

[4]Li J Z.A note on the finite-time ruin probability of a renewal risk model with Brownian perturbation[J].Statistics&Probability Letters,2017,127(3):49-55.

[5]Guo F L,Wang,D C,Yang H L.Asymptotic results for ruin probability in a two-dimensional risk model with stochastic investment returns[J].Journal of Computational and Applied Mathematics,2017,325(4):198-221.

[6]Eryilmaz S,Gebizlioglu O L.Computing finite time non-ruin probability and some joint distributions in discrete time risk model with exchangeable claim occurrences[J].Journal of Computational and Applied Mathematics,2017,313(1):235-242.

[7]Dimitrova D S,Kaishev V K,Zhao S Q.On the evaluation of finite-time ruin probabilities in a dependent risk model.Applied Mathematics and Computation[J],2016,275(1):268-286.

[8]Borovkov A A.Probability Theory[M].Springer,2013:110-120.

[9]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社，2004：159-160．

[10]林正炎，白志东.概率不等式[M].北京：科学出版社，2006：78-79．