一类分数阶微分方程边值问题解的存在性

王文倩，马凡婷，孙 芮

（兰州交通大学 数理学院，甘肃 兰州730070）

分数阶微积分是处理任意阶微积分研究及应用的数学分析领域，其微分与积分不再局限于整数，可以是任意的实数或者复数。1832年Liouville提出了分数阶微分定义，并用该定义成功解决了势理论问题。1847年Riemann对分数阶微积分定义做了进一步修正和补充。研究和应用比较多的两种定义是Caputo定义和Riemann-Liouville定义。目前对分数阶微分方程研究主要集中在初值问题、边值问题、周期解、分数阶微分系统的稳定性、能控性以及微分包含问题等方面[1-9]。

2010年Zhou等考虑如下边界值问题[10]

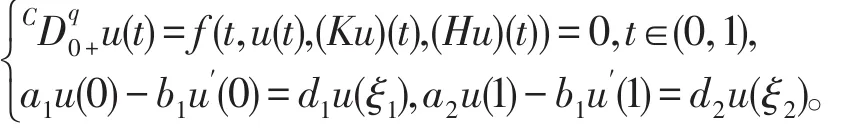
2012年Bashir Ahmad等讨论了分布边界值条件的分数阶微分方程的边值问题[11]

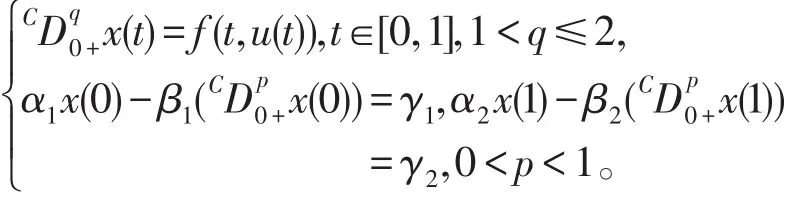
受到上述文献的启发，主要研究下述分数阶微分方程边值问题

1 预备知识

引理 1[12]设α＞0,若x∈C(0,1)⋂L[0,1],α＞0,则分数阶微分方程的唯一解可表示为

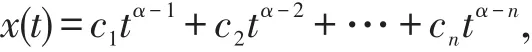
其中，n-1＜α≤n,ci∈R,i=1,2,…,n∈N。

引理 2[12]设α＞0,若x∈C(0,1)⋂L[0,1]有α阶导数，且∈C(0,1)⋂L(0,1),则

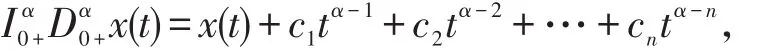
其中，n-1＜α≤n,ci∈R,i=1,2,…,n,n∈N。

引理3 设h(t)∈C[0,1],则下述问题

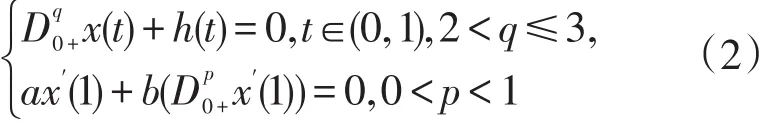
其中

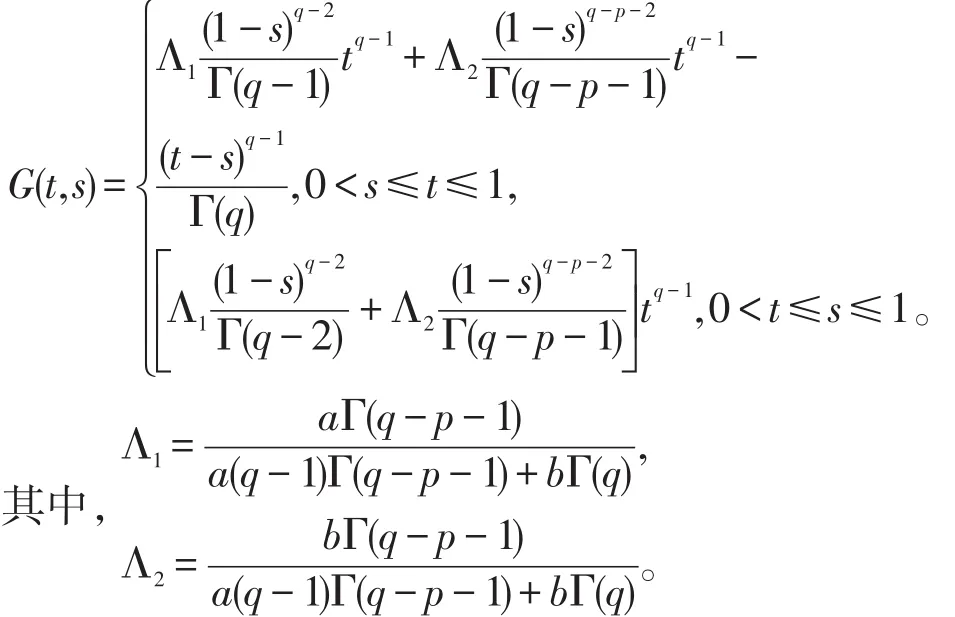
证明 假定x(t)满足（1），由引理1可得

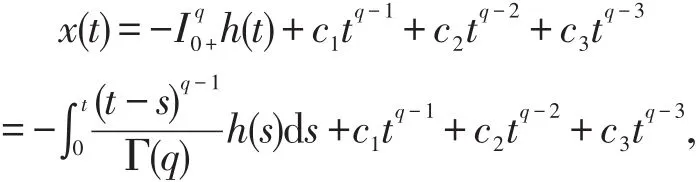
从而

可知c2,c3=0。再利用及 (1)得

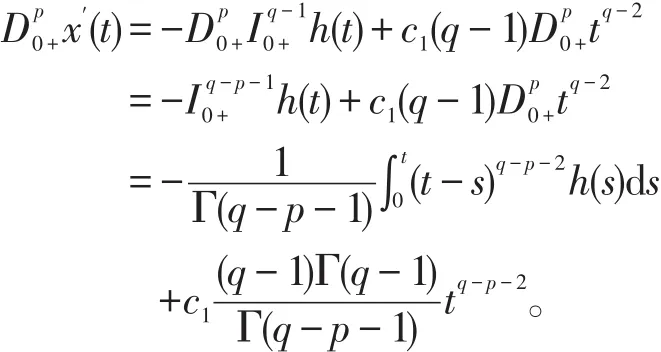
由边界条件可得

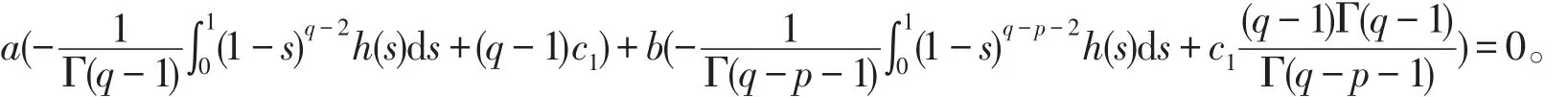
从而得出

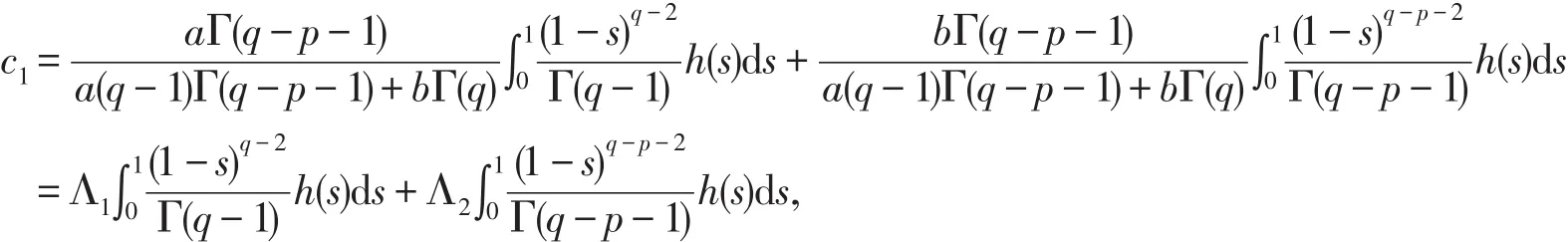
故

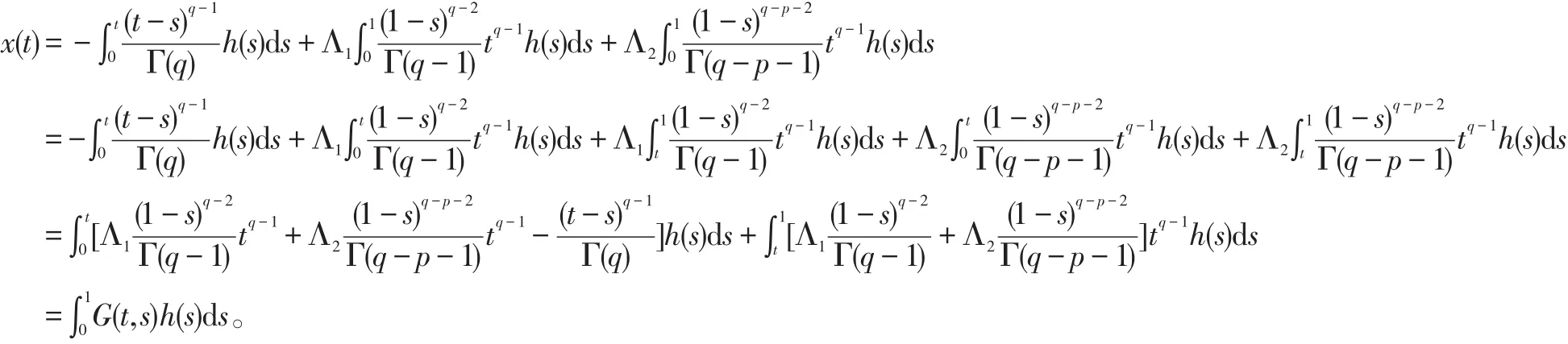
2 主要成果

为了得出所要的结论，给出如下的假定：

(H1)函数f:J×R→R为连续函数，且存在非负常数L,使得|f(t,u)-f(t,v)|≤L‖u-v‖,L＜1,对任意t∈J,u∈R都成立。

(H2)存在常数μ使得λ≤μ＜1,t∈J,其中

定理 1 假设(H1)和(H2)成立，则方程(1)在C(0,1)上有唯一解。

证明 由引理3，方程(1)有解当且仅当算子方程Tx=x有不动点。

第一步，定义算子如下

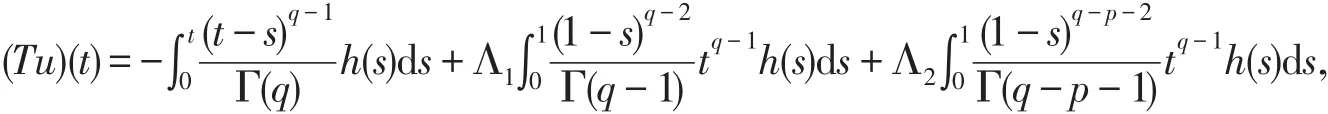
则

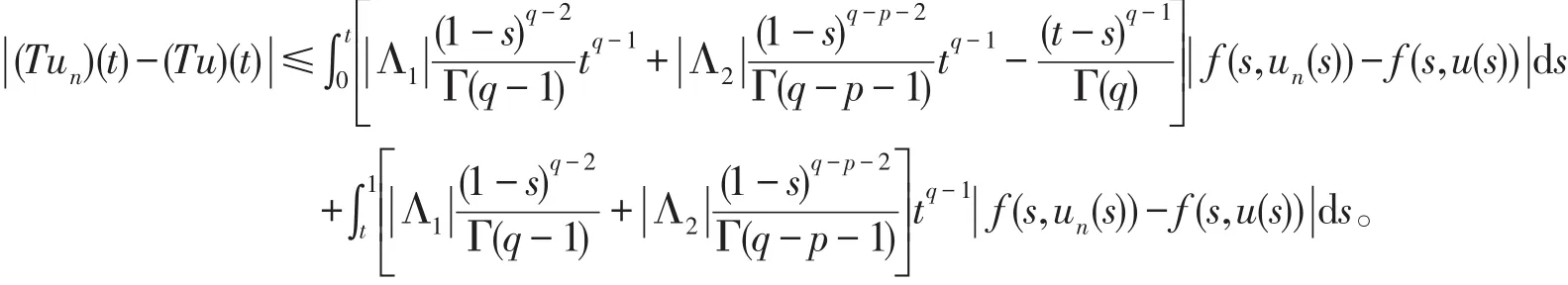
因为f为连续函数，所以当n→∞时有‖(Tun)(t)-(Tu)(t)‖ →0,所以T:C[0,1]→C[0,1]连续。

第二步，考虑集合DM={y∈C[0,1]:‖y‖≤M},且存在正常数M＞0使得|f(t,u)|≤M，显然DM是C[0,1]的闭凸有界集。下面证明T(DM)⊂DM,对∀u∈DM,有

因此，‖(Tu)(t)‖≤M。

第三步，证明T为压缩映射，对于u,v∈C[0,1]和对每一个t∈[0,1]，由(H1)可以得到

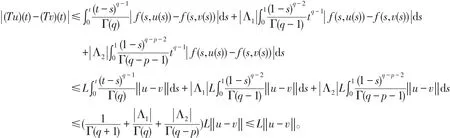
由于L＜1,因此T是一个压缩映射。由压缩映像原理，可以得出T有唯一不动点也即是方程(1)的唯一解。

3 举例

例1 考虑分数阶微分方程边值问题

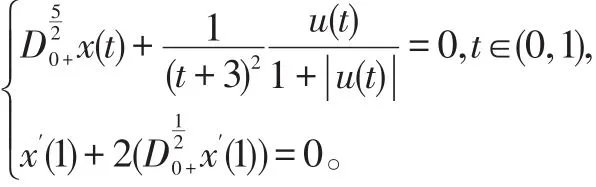
解 显然，

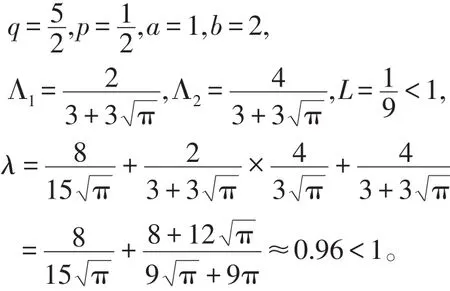
满足定理1的条件，此边值问题有唯一解。

4 小结

文章给出了Riemann-Liouville分数阶导数的基本理论，研究了在Riemann-Liouville分数阶导数2＜q≤3的前提下，与经典分析类似，通过定义合适的线性空间以及范数，设定合适的算子，在满足一定的条件下，利用压缩映像原理得出了分数阶微分方程解的存在性和唯一性的条件。

参考文献：

[1]Baleanu D,Diethelm K,Scalas E,et al.Fractionsl Calculus Modelsand Numerical Methods[M].Boston:World Scienti fic,2012.

[2]Zhou W X,Chu Y D.Existence of solutions for fractional differential equations with multi-point boundary conditions[J].Communications in Nonlinear Science and Numerical Simulation，2012,17(3):1142-1148.

[3]Zhou W X，Peng J G，Chu Y D.Multiple positive solutions for nonlinear semipositone fractional differential equations[J].Discrete Dynamics in Nature and Society，2012:1-10.

[4]Zhou W X,Liu H Z.Existence of weak solutions for nonlinear fractional differential inclusion with non-separated boundary conditions[J].Journal of Applied Mathematics,2012:1-13.

[5]Zhou W X，Chu Y D，Balean,D.Uniqueness and existence of positive solutions for a multi-point boundary value problem of singular fractional differential equations[J].Advances in Difference Equations,2013:100-114.

[6]Zhou W X,Liu H Z.Existence solutions for boundary value problem of nonlinear fractional q-difference equations[J].Advances in Difference Equations,2013,113:1-12.

[7]Zhi E T,Liu X P,Li F F.Nonlocal Boundary Value Problem for Fractional Differential Equations with p-Laplacian[J].Mathematical Methods in Applied Science,2014,37(17):265-266.

[8]Lakahmikantham V,Leela S,Devi J V.Theory of Fractional Dynamic Systems[M].Cambridge:Cambridge Academic Publishers,2009.

[9]Sabatier J,Agrawal O P,Machado J T.Advances in Fractional Calculus.Theoretical Developments and Applications in Physics and Engineering[M].Dordrecht:Springer,2007.

[10]Zhou W X,Chu Y D.Existence of solutions for fractional differential equations with multi-point boundary conditions[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(3):1142-1148.

[11]Ahmad B,Ntouyas S K.A Note on fractional differential equations with fractional separated boundary conditions[J].Abstract and Applied Analysis,2012,12:1-11.

[12]Bai Z B,Lü H S.Positive solutions for boundary value problems of nonlinear fractional differential equations,Journal of Mathematical Analysis and Applications,2005,(311):495-505.