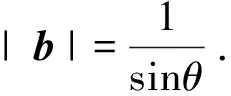不忘初心 回归本源
——平面向量高考题赏析
浙江兰溪市游埠中学
陈 晓 (邮编:321106)
平面向量在高考中占的比重不是很大,往往只是一两个小题.但是向量集代数、几何于一身,倍受命题者的青睐,许多全国卷和地方卷的高考题把平面向量放在小题的压轴位置.细细品味向量试题别有一番风味.
笔者认真梳理了2017年高考向量真题,发现许多向量试题都离不开平行四边形,或来源于平行四边形,或用平行四边形求解.平行四边形简直可以称为向量的“神图”.

图1

(a+b)2=a2+2a·b+b2
①
(a-b)2=a2-2a·b+b2
②
①+②得
(a+b)2+(a-b)2=2(a2+b2)
③
恒等式③在人教A版必修4第二章第五节的例1出现过,其意义就是平行四边形对角线的平方和等于四条边的平方和.
①-②得(a+b)2-(a-b)2=4a·b
④
恒等式④称为极化恒等式,它沟通了向量的线性运算和数量积运算.
笔者选取部分高考向量真题,与广大师生一同品味.
类型一巧构“神图”速解小题
例1(2017年全国卷2文)设非零向量a、b,满足|a+b|=|a-b|,则
A.a⊥bB. |a|=|b|
C.a∥bD. |a|>|b|
解析如图1,以a、b为邻边作一平行四边形,由a⊥b可知该平行四边形为矩形,所以|a+b|=|a-b|.
例2(2017年全国卷1理)已知向量a、b的夹角为60°,|a|=2,|b|=1,则|a+2b|=______.

图2

图3

图4





图5

图6
则
A.I1 B.I1 C.I3 D.I2 所以I3 经典回顾(2014年浙江卷)设θ为两个非零向量a,b的夹角.已知对任意实数t,|b+ta|的最小值为1,则( ) A.若θ确定,则|a|唯一确定 B. 若θ确定,则|b|唯一确定 C.若|a|确定,则θ唯一确定 D. 若|b|确定,则θ唯一确定 图7 类型二两个恒等式的应用 例5(2017年浙江卷)已知向量a、b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______,最大值是______. |a+b|+|a-b| 例7(2017年浙江卷)如图8,已知抛物线x2=y,点 抛物线上的点P(x﹐y) 过点B作直线AP的垂线,垂足为Q. 图8 (Ⅰ)求直线AP斜率的取值范围; (Ⅱ)求|PA|·|PQ|的最大值. 所以|PA|·|PQ|=2-|PM|2. 记 因为f′(x)=4x3-3x-1= 经典回顾(2012年安徽卷)若平面向量a,b满足|2a-b|≤3,则a·b的最小值是______. 高考真题是命题专家智慧的结晶,更具代表性和科学性.高三备考很多时候深陷题海战术不能自拔,做了大量的模拟题而成绩却很难提高,究其原因无外乎选题和做题两方面出问题了.事实上虽然高考题每年都不一样,但许多试题的背景和解法并没有变.比如本文提到的两个恒等式, 2012-2014年的浙江卷连续出现三年.因为向量兼具代数和几何,所以很多时候解平面向量的题目只需要画个图(比如本文提到的平行四边形)就能完成.建议考生翻阅浙江卷(2004年—2017年)的平面向量试题,许多题目都是可以作图完成的.总之,年年岁岁解相似,岁岁年年题不同.