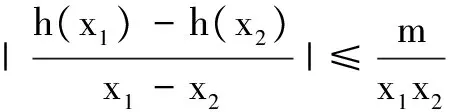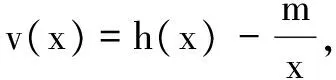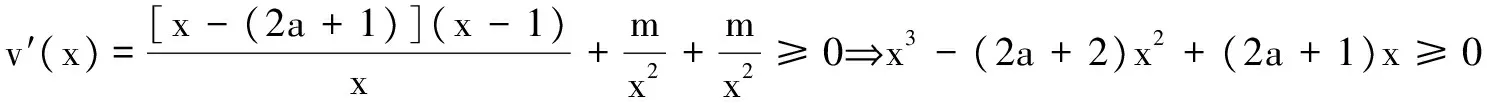识得双变量 且辨构造法

韩长峰 卫小国

(1.安徽省阜阳太和中学 236600; 2.山东省单县第一中学 274300)

卫小国(1979-)，男，汉，湖北武汉人，山东省单县第一中学数学教师，主要数学解题教学研究、数学建模与自主招生试题研究.

一、常规的偏移问题—消元构造

例1 (2016年高考课标Ⅰ卷理)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1,x2是f(x)的两个零点,证明：x1+x2<2.

解(1)a的取值范围(0,+∞).

接下来证明：∀x∈(-∞,1)g(x)-g(2-x)>0；也即要证∀x∈(-∞,1),ex(2-x)-xe2-x>0.令h(x)=ex(2-x)-xe2-x.

则h′(x)=(ex-e2-x)(1-x)，易知当x<1时，ex-e1-x<0.

于是，在(-∞,1)上，h(x)=ex(2-x)-xe2-x单调递减且h(1)=0，即可证得.

评注解决函数不等式的证明问题，思路是构造适当的函数,利用导数研究函数的单调性或极值破解.而极值偏移问题，要另借对称和整体思想构造函数；本质上是将双变量通过消元转化为极值点一侧的单调性研究.

(1)求f(x)的单调区间；

(2)证明：当f(x1)=f(x2)(x1≠x2)时，x1+x2<0.

二、对数均值不等式——换元构造

(1)求实数a的取值范围；

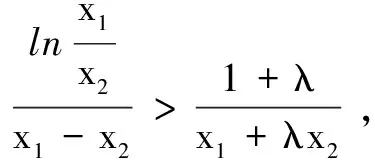
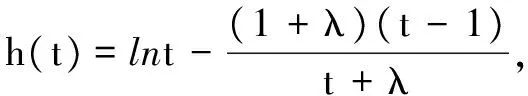
当λ2≥1时，可见t∈(0,1)时，h′(t)>0，

所以h(t)在t∈(0,1)上单调增，又h(1)=0，则h(t)<0在t∈(0,1)恒成立，符合题意．

当λ2<1时，可见t∈(0,λ2)时，h′(t)>0，t∈(λ2,1)时h′(t)<0,所以h(t)在t∈(0,1)上不能恒小于0，不符合题意，舍去．

综上所述，λ≥1.

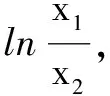
类似的试题有: (2014年天津卷)设f(x)=x-aex.已知函数y=f(x)有两个零点x1,x2，且x1

三、绝对值类双变量—分离构造

含绝对值型函数，常规是要分类讨论,而若与双变量结合，通法显然无能为力，只有充分利用函数的性质，将绝对值“剥离”，为分离构造提供条件.具体操作，且以下题为例进行分析.

例3 (2017年山东潍坊市一月检测)已知函数f(x)=x2-x,g(x)=lnx.

若a∈[e,3],∀x1,x2∈[1,2](x1≠x2),

当a∈[e,3]时，2a+1∈[2e+1,7]，故h(x)在[1,2]上单调递减.

不妨设1≤x1h(x2).

当x∈[1,2]时，2x-2x2≤0，可知只需a∈[e,3]时， 3(2x-2x2)+x3-2x2+x+m≥0⟹x3-8x2+7x+m≥0,x∈[1,2].

不难求得m的取值范围是[10,+∞).

评注绝对值的消除，是借函数的单调性进行的，而后将x1,x2分列于不等式两侧，试题化为某一函数的单调性的论证与求参问题.

类似的试题有: ( 2016年皖西十校联考)已知f(x)=(a+1)lnx+ax2+1; (2)当a≤-2时求证：对任意x1,x2∈(0,+∞)都有 |f(x1)-f(x2)|≥4|x1-x2|.

参考文献：

[1]邢友宝.极值点偏移问题的处理策略[J]. 中学数学教学参考(上旬),2014(7)：19-22.

[2]蓝云波,何洪标.活跃在各类考试中的对数平均不等式[J]. 数学教学,2016(5)：22-25.