例谈区域染色问题

李 维

(甘肃省会宁县第四中学 730799)

排列组合的染色问题是一个广大学生在学习中难以掌握的知识，经常我们看到的是颜色与染色区域相同问题，有些时候我们看到的并不是这样，看到的是颜色种数多于染色区域，或颜色种数少于染色区域，或者不同区域或者不同图形等等，这些问题如何解决呢，下面就经常见的三类问题谈几点，供大家商讨.

一、颜色种数与区域相同问题

解决的办法是以颜色在区域内相同与否分类解答.

例1 用4种不同的颜色涂入图1中矩形A,B,C,D框中，要求相邻的矩形涂色不同，则不同的涂色办法有多少种？

图1

解析如图1这类问题可分两类：

(1)若A,B,C,D四个区域颜色不一样，有N1=4×3×2×1(种).

(2)若A,D涂同色.或B,D涂同色，则有N2=4×3×2+4×3×2(种).

故由上述可得不同涂色办法有N=N1+N2=4×3×2×1+4×3×2+4×3×2=72(种).

二、颜色种数多于染色区域问题

解决的办法按照区域的染色的颜色种数分类解答.

例2 设直线x=0和y=x将圆x2+y2=4分成四部分，用5种不同的颜色给四部分涂色，要求每一部分涂一种颜色，且相邻的区域不能为同色，则不同的涂色方案有多少种？

解析由已知这个题目的染色区域有四个区域，故颜色多于区域，故要对颜色先取再涂色的方法，故这个问题分三类解决.

(1)选用4种颜色涂色，每一部分用一种颜色，故有方法

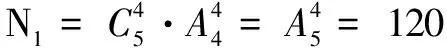
(2)选用3种颜色涂色，有两部分用一种颜色，又分为两种，可有

(3)选用2种颜色涂色，则每两部分颜色相同，故有

由上述可得所有的方案种数共有

N=N1+N2+N3=260(种).

三、颜色种数少于染色区域

方法是先染一区域，再确定其他区域染色方法.

例3 将一个四棱锥的每个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有5种颜色可供使用，求不同的染色方法种数.

解析这个题是一个立体几何的染色问题，与平面图形基本一样，先将四棱锥一侧面的三顶点染色，再考察其他的顶点的染色数，用分步计数原理即可得出结论.

如图2所示，有题设四棱锥S-ABCD的顶点S,A,B所染的颜色互不相同，它们共有5×4×3=60种方法，当S,A,B染好后不妨设颜色分别是1，2，3.当S染1时，若C染2，则D可染3或4或5，有3种染法；若C染4，则D可染3或5，有2种染法；若C染5，则D可染3或4，有2种染法.可见，当S,A,B染好后，C,D还有7种染法，故不同的方法有60×7=420(种)

图2

实弹演练

1.如图3，一个地区分为5个行政区域，现给地图着

色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有________种(以数字作答)

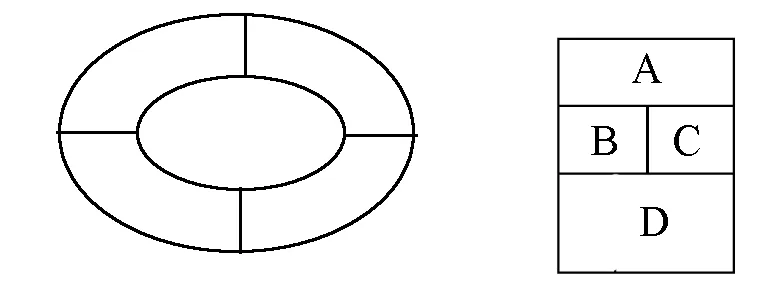
图3 图4

2.如图4,用5种不同颜色给图中A,B,C,D 4个区域涂色，规定每个区域只涂一种颜色，相邻区域涂不同颜色，则不同的涂色方法有________种

答案1. 72种 2. 180种

参考文献：

[1]方勇.条形、环形区域染色问题的完美解决[J].中国校外教育,2010(15).