绕开极限——谈两个不等式在函数估值中的应用

马必武

(福建省福鼎市第一中学 355200)

由于中学阶段学生没有系统地学习过极限理论，在函数与导数的有些题目中有些老师会用极限理论来说明函数图象的逼近过程等，这会对学生造成不必要的负担.同时在客观题中用极限说明估且可以，但在解答题中就不行了.因此就要用到函数估值的方法，而不等式ex≥x+1和x-1≥lnx在函数估值中有很强的应用，现就举例说明.

例1 (2017年全国Ⅰ卷理科第21题)已知函数

f(x)=ae2x+(a-2)ex-x，

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点，求a的取值范围.

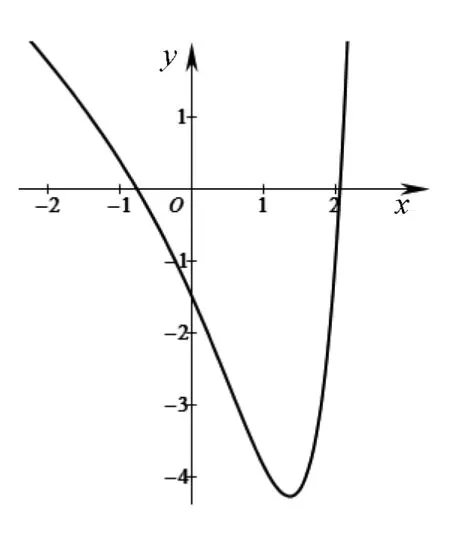
图1

解析(1)略.

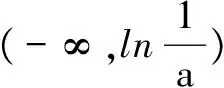
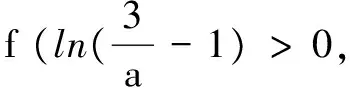
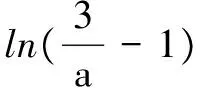
其实要使f(x)>0，

即ae2x+(a-2)ex-x>0，

也就是ax(aex+a-2)>x.

①

例2 已知f(x)=lnx-ax+1，若f(x)有两个零点，求实数a的取值范围.

图2

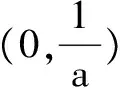
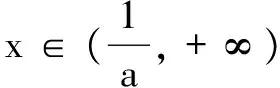
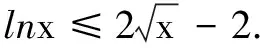
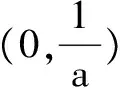
因此f(x)有两个零点时:0

因此在有些函数的零点判断中要说明函数值是正的或负的时不能用极限来说明就要考虑到利用不等式 和 来进行放缩，这样就能找到 使得函数值是正的或负的.

参考文献：

[1]许清波.导数与不等式[J].高中生之友,2006(Z3).