从高考试题看高中数学圆锥曲线解题技巧

周 晓

(福建省霞浦第一中学 355199 )

一、直线与圆锥曲线位置关系中，求直线参数问题

直线参数作为直线与圆锥曲线位置关系中经典出题方式，这类题型经常在数学高考中出现，主要考查了学生是否熟练掌握了圆锥曲线定义和简单的几何性质，能否运用对未知数“设而不求”与数形结合等方法的解题思想.对于求直线参数这类题时必须要细心审题和画图，虽然这种类型的题目难度不大，但是由于粗心就非常容易导致出错，所以考试的时候必须要仔细看清数字和字母，做完题后要反复检查.

例1 (2016年全国卷)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(1)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

图1 图2

解(1)圆心为A(-1,0)，圆的半径为AD=4,因为AD=AC，所以∠ADC=∠ACD.又因为BE∥AC,所以∠ACD=∠ADC=∠EBD,

因为BE=ED，所以|EA|+|EB|=|AD|=4.

所以点E的轨迹是以点A(-1,0)和点B(1,0)为焦点，以4为长轴长的椭圆，

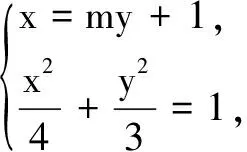
二、圆锥曲线中的直线过定点的问题

(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

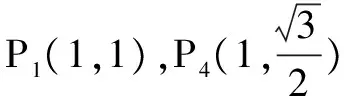
(2)设直线P2A与直线P2B的斜率分别为k1，k2，

如果l与x轴垂直，设l：x=t，由题设知t≠0，且

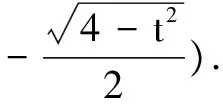
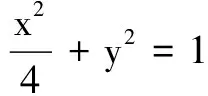
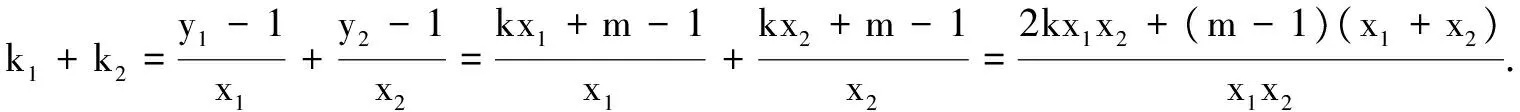
由题设k1+k2=-1，故(2k+1)x1x2+(m-1)(x1+x2)=0.

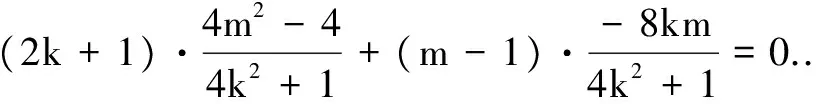
参考文献：

[1]马晨阳. 圆锥曲线参数方程在高中数学解题中的应用浅析[J].教育科学(引文版)，2017，9(16).

[2]雷鹏.圆锥曲线参数方程在高中数学解题中的应用[J].学周刊,2016(9):134.