排列组合中的几对互否问题

柳 华

(山东省临沂市中医药职工中等专业学校 276017)

一、“一”与“多”

例1 三封信投入4个信箱，有____种不同的投法；三名运动员争夺四个项目的金牌，有____种不同的方法.

分析可以利用公式“一”的“多”次幂进行求解.

“一”个信箱可以容纳“多”封信，故信箱数为“一”，信的封数为“多”，故有43种不同的投法；

“一” 名运动员可以拿“多” 枚金牌，故运动员数为“一”，金牌数为“多”，故有34种不同的争夺方法.

评注辨清“一”与“多”是解题的关键.

二、邻与不邻

例2 有两排座位，前排11个座位，后排12个座位.现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同的排法种数为____.

分析若直接从正面解答，较为复杂.可从反面考虑，总的坐法中减去这两人左右相邻的情况即可.

评注相邻问题捆绑法，不相邻问题插空法，这两类问题可互相转化，相互为用.

三、在与不在

例3 数学、语文、外语、物理、化学、体育；六门科目，安排在一天的六节课内，要求体育不在第一节，数学不在第六节，共有____种不同的排法.

分析数学可排在除第六节外的五节课内，但数学是否排在第一节将影响到体育课的排法.故应分成两类：

评注在与不在问题应优先考虑限制条件，当条件发生冲突时，应分类解决.

四、含与不含

例4 从1、3、5、7中任取2个数字，从0、2、4、6、8中任取2个数字组成没有重复的四位数，能被5整除的共有____个.

分析取出的数字含5或0的情况影响到排法，故分三类：(1)四位数中含5和0的情况：

(2)四位数中含5不含0的情况：

(3)四位数中含0不含5的情况：

综上，四位数总数为120+108+72=300.

评注含与不含问题按取舍分类讨论.

五、平均分组与非平均分组

例5 将4名教师分配到3所学校任教，每所学校至少1名教师，则不同分配方案有____种.

分析将4名教师分成3组，全排列即可.

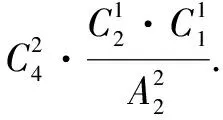
评注理解平均分组的特殊性.

六、有序与无序

例6 某校高二共6个班，现从外地转入4名学生，安排到2个班中，每班2名，不同安排方法种数为____种.

七、同与不同

例7 将4个相同的小球放入编号为1、2、3、4的四个盒子中，恰有一个空盒的放法种数为____.

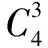
评注球相同时，仅注意个数就可以了.

八、至少与至多

例8 在100件产品中有2件次品，抽出的3件至少有1件次品的抽法有____种.

分析题中至少有1件次品包含两类，1件次品和2件次品，其反面为没有次品，因此有以下两种方法.

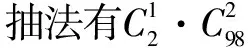
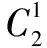
参考文献：

[1]张金良.数列错解典例剖析[J].中学理科,2005(08).

[2]李军.高中数学数列问题常见错解简析[J].学园,2014(09).