构造函数 巧解不等式

惠丹凤 吴丽芳 魏春强

(陕西省安康学院数学与统计学院 725000)

吴丽芳( 1995.9-)女，陕西省汉中人，2014级数学与应用数学专业学生.

魏春强(1964.9-)，男，陕西省城固人，本科，从事高中数学教育研究.

不等式的证明方法有多种，但是由于其自身的复杂性，我们通常可以根据不等式的自身特征，构造适当的函数利用其单调性、奇偶性、有界性、凹凸性巧解不等式.

一、构造函数，利用单调性

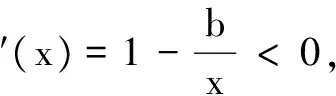
解法小结此题具有较强的函数背景，通过分析直接构造出相应函数，利用导数法和它的单调性质就可简捷地证明了此不等式.

二、构造函数，利用有界性

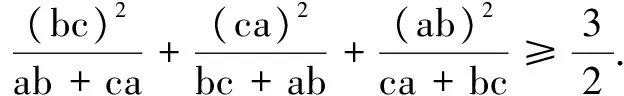
解法小结此不等式需要变换形式再构造，利用导函数的几何意义构造有界函数，即变元取平均值时的切线函数，最后即证此不等式成立.

三、构造函数，利用奇偶性

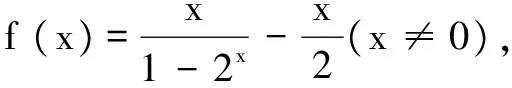
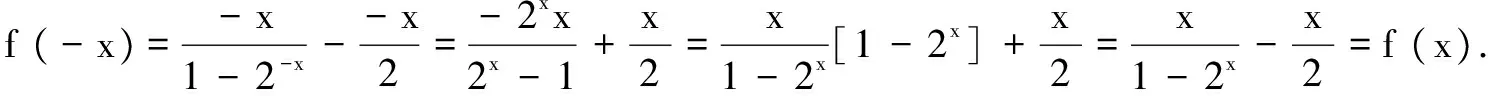
解法小结本题是通过不等式特征构造函数，再借助函数的奇偶性和图象的对称性达到证明.

四、构造函数，利用凹凸性

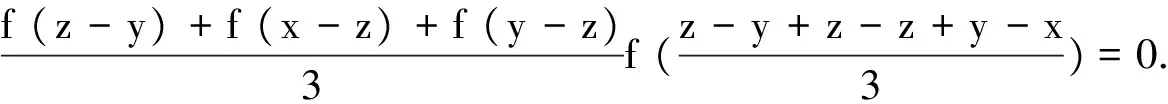
解法小结本例题先通过变换形式再构造函数，利用函数的凹凸性，最终证明不等式成立.

因此，通过对以上例题的分析，我们发现，构造函数法在证明不等式中有着共同独特的魅力，因为函数的单调性、奇偶性等性质的应用，常常使得不等式的证明由复杂变得简单，达到了意想不到的效果.

参考文献：

[1]陈传理，张同君.竞赛数学教程(第三版)[M].北京：高等教育出版社，2013：26-29.

[2]韩清海，张凤民.新编高中总复习导与练——数学[M].陕西：陕西人民出版社，2005：235.