污水处理决策优化控制
栗三一 乔俊飞 李文静 顾锞
污水处理可有效缓解水资源匮乏问题和减少环境污染[1−2].然而污水处理过程的控制面临以下难题[3]:1)生化反应过程十分复杂,拥有众多变量且变量之间耦合严重;2)流入污水的浓度和流量是时变的;3)在出水达标的情况下需要尽可能降低能耗、提高水质.
针对污水处理过程控制问题,国内外学者做了大量研究.Mulas等[4]将多变量预测控制应用于市政污水处理的活性污泥过程,以最小化经济花费和提高总氮去除率为目标,使用动态矩阵控制算法控制水总氮浓度(SNtot,e),实验表明该方法可以同时减少能耗和降低SNtot,e峰值.Sant´ın等[5]针对污水处理过程提出一种二级分层控制结构,使用模糊控制动态调节第五分区溶解氧浓度(SO,5)设定值,底层使用模型预测控制器对SO,5进行跟踪控制,达到降低能耗和提高水质的目标.Egea等[6]以能耗和水质为目标,使用epsilon约束和分散搜索技术搜索pareto解,直接对第五分区氧转换系数(KLa,5)和内回流量(Qa)进行控制.Yang等[7]使用模糊c均值聚类方法和最小二乘方法对污水处理过程建立模糊模型,根据模糊模型设计模型预测控制器对SO,5进行控制,实验表明该控制器在暂态过程和稳态过程都有很好的控制效果.Vega等[8]将非线性模型预测控制应用于污水处理分层控制,在优化层分别使用静态优化算法和动态优化算法对SO,5和第二分区硝态氮浓度(SNO,2)进行优化,底层跟踪控制使用非线性模型预测控制,该控制策略在固定设定值、PID控制的基础上降低20%能耗.Han等[9]对污水处理过程提出非线性多目标模型预测控制方法,该方法使用自组织径向基函数(Radial basis function,RBF)神经网络建立预测模型,使用多目标梯度优化方法对SO,5和SNO,2进行动态调节,以达到降低能耗的目标.以上研究以提高水质或减少能耗为目标,取得了令人满意的效果,但忽视了出水氨氮浓度SNH,e和SNtot,e峰值超标的问题.SNH,e和SNtot,e超标不仅会污染环境、危害人体健康,而且会因排污超标受到罚款,造成污水处理厂的经济损失.
在解决SNH,e和SNtot,e峰值超标问题方面,Sant´ın等[10]于2016年首次提出污水处理决策控制方法.该方法以入水流量、入水氨氮浓度预测SNH,e和SNtot,e,对外加碳源量和Qa进行模糊控制,从而达到抑制SNH,e和SNtot,e峰值的目的.该方法有效抑制了SNH,e和SNtot,e峰值,但存在能耗较大的问题.
以在抑制SNH,e和SNtot,e峰值的情况下降低能耗为目标,本文提出污水处理决策优化控制方法.首先使用神经网络建立SNH,e和SNtot,e预测模型;然后使用局部搜索NSGA2算法对能耗和水质进行优化,结合预测模型从Pareto解中选取合适的解作为溶解氧和硝态氮浓度设定值;最后根据预测模型的输出判断SNH,e和SNtot,e是否超标.如果超标,则使用模糊控制方法对外部碳源和Qa进行控制,抑制峰值.如果不超标,则使用模糊控制器控制Qa和KLa,5对设定值进行跟踪控制.本文提出方法的优势在于:
1)将SO,5和SNO,2加入预测模型输入.由于SO,5和SNO,2对SNH,e和SNtot,e有重要影响[11],将其加入预测模型输入端,提高了预测模型的精度.
2)提出时滞时间计算方法.根据每天的入水氨氮和SNH,e峰值时间差估算延迟时间,对建立预测模型数据采样提供支持.
3)为了避免多目标进化算法陷入局部最优,使用基于密度的局部搜索NSGA2算法(NSGA2-DLS)[12]对能耗和水质进行优化,在出水达标的情况下有效地降低能耗.
4)将预测模型应用于最优解的选取过程,从而将优化控制与决策控制有机结合.该最优解选取策略可以优先通过调节设定值确保出水水质达标,从而尽可能降低能耗.
5)预测模型可以预测一段时间之后的SNH,e和SNtot,e,从而可以根据预测结果进行提前控制,有效抑制峰值超标.
1 建立预测模型
考虑到污水处理是一个大滞后过程,根据当前入水情况建立预测模型,预测一段时间之后的出水污染物浓度,从而可以根据预测结果进行提前控制.
1.1 数据采集
本文以活性污泥污水处理基准仿真模型BSM1[13]为实验平台进行数据采样和实验验证.首先使BSM1模型开环运行14天,记录入水氨氮浓度、第二分区氨氮浓度、第五分区氨氮浓度和SNH,e,其浓度变化曲线如图1所示.记录每天各区域氨氮浓度峰值对应的时刻,计算每天从入水到第二分区、第五分区和出水的滞后时间,每天的滞后时间如表1所示.

表1 不同区域到入水氨氮浓度最大时刻滞后时间(h)Table 1 The time lag from in flow to different regions(h)
然后根据每天的滞后时间对数据进行采样.由于SO,5和SNO,2对SNH,e和SNtot,e有重要影响[11],本文以入水流量、入水氨氮、当前出水氨氮浓度、SO,5和SNO,2作为SNH,e预测模型输入变量,以入水流量、入水总氮、当前出水总氮浓度、SO,5和SNO,2作为SNtot,e预测模型输入变量.根据实际经验将SO,5浓度设定值设定在1.4~2.4mg/l,SNO,2浓度设定值设定在0.5~1.5,设定值设定后即在BSM1模型上运行14天,每15分钟采样一次,取不同的设定值的组合方式,共获得199727组数据.
1.2 神经网络建模
本文使用前馈神经网络建立出水氨氮和总氮浓度预测模型,模型示意图如图2和图3所示.两个神经网络模型的结构均为5-50-1(试错法确定隐含层神经元数).将采样获得的199727组数据随机选取181570组作为训练样本,剩余数据作为测试样本.权值初始化采用文献[14]提出的方法,训练时将数据归一化到[−1,1],使用BP算法对网络进行训练[15],初始学习率设为0.1,最大学习步数为4000步.模型测试均方根误差(Root mean square error,RMSE)如表2 所示.Sant´ın 等[10]建立预测模型时仅将入水氨氮浓度、入水流量和温度作为预测模型的输入,本文将对SNH,e和SNtot,e有重要影响的SO,5和SNO,2加入输入变量,从表2的结果可以看出,将SO,5和SNO,2加入模型输入端有效提高了预测模型的精度.

图2 出水氨氮浓度预测模型Fig.2 Prediction model ofSNH,e

图3 出水总氮浓度预测模型Fig.3 Prediction model ofSNtot,e

表2 预测模型测试均方根误差(10次实验平均值)Table 2 Test RMSE of prediction model(mean value of ten test results)
污水处理过程中各变量耦合严重,对SNH,e和SNtot,e浓度有影响的变量很多,根据机理分析和已有的研究[10−11,16],本文选取影响最大的五个变量作为模型输入,但预测值不可避免与实际值存在误差,下面讨论该误差对本文提出的控制策略的影响.
在BSM1平台上进行开环运行14天,使用建立的预测模型对SNH,e和SNtot,e进行预测并与实际值进行对比,仿真结果如图4和图5所示.图中实线曲线表示实际浓度曲线,虚线表示模型预测曲线,从图4和图5可以看出,每天城市污水的出水量是不断变化的,而且最高值和最低值相差比较大,在国家规定的浓度上限值(SNH,e和SNtot,e的上限值分别为4mg/l和18mg/l)附近曲线的变化率很大,模型在该上限值附近预测误差并不大.共存在四种情况,下面分别进行讨论.

图4 出水氨氮浓度预测曲线Fig.4 Prediction curve and actual curve ofSNH,e
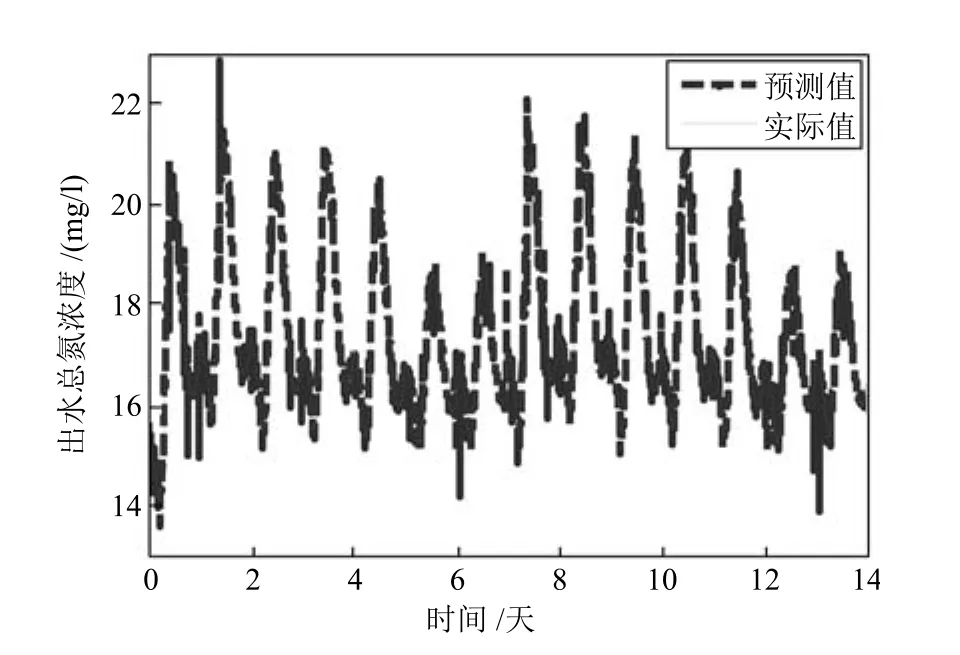
图5 出水总氮浓度预测曲线Fig.5 Prediction curve and actual curve ofSNtot,e
第一种情况是峰值超标严重,从图4和图5可以看出,最多提前或滞后半小时启动应急操作,对于污水处理这样的慢反应过程而言在可接受范围之内.根据实际情况,当对污水处理过程没有相应操作时,出水不会长时间固定在国家标准附近,也就是说不存在长时间误判超标的情况.
第二种情况是峰值超标但超标值很少,从图中可以看到,峰值持续时间都比较短,即使误判为没有超标,出水氨氮和总氮浓度也会很快降到标准以下,因此这种情况影响不大.
第三种情况是峰值接近上限值但没有超标,这种情况可能存在误判超标从而启动应急操作.从实验结果可以看到,误判的时间持续很短暂,在1~2个小时内就会达到终止应急操作的条件,因此造成的损失有限.
第四种情况为峰值距离上限值较远,这种情况下判断基本准确,不会进行误操作.
从以上分析可以看出,出水氨氮和总氮预测模型的输出与实际值存在偏差,但对实际操作造成的损失并不大,即使误判也会在较短时间内更正操作.
2 设定值动态优化
SO,5和SNO,2不仅对SNH,e和SNtot,e有重要影响,而且直接受KLa,5和Qa的影响,对其浓度设定值进行优化可以有效降低能耗[11].因此本文首先使用神经网络建立能耗模型和水质模型作为优化目标函数,然后使用多目标进化算法对目标进行优化,结合之前建立的预测模型挑选合适的解作为SO,5和SNO,2的设定值.
2.1 建立能耗、水质模型
使用多目标优化算法调整SO,5和SNO,2设定值,首先需要确定目标函数.根据课题研究背景,将能耗和水质作为优化算法的两个目标函数.由于污水处理过程影响能耗和水质的因素众多,且各影响因素之间关系复杂,能耗模型和水质模型难以直接获得.本文使用前馈神经网络建立能耗和水质模型.
能耗模型和水质模型输入变量均为出水悬浮物浓度、SNH,e、SO,5和SNO,2[17].数据采集不考虑时间延迟,每15分钟采集一次数据,数据采集方法与第1.1节相同,SNO,2浓度设定值和SO,5浓度设定值在取值范围内取不同的数值在BSM1平台上进行实验,共记录295669组数据进行建模,其中268790组数据用于训练,26879组数据用于测试,模型结构4-40-1(试错法确定隐含层神经元数).参数设定和训练方法与建立预测模型相同.能耗模型测试RMSE为0.0883,水质模型测试RMSE为0.4202.
2.2 优化问题模型
污水处理过程优化问题可以表示为以下数学形式:

其中,F1和F2为两个目标函数,分别代表能耗和水质;f1和f2为第2.1节建立的能耗模型和水质模型;决策向量X的两个元素(x1,x2)分别表示第五分区溶解氧浓度和第二分区硝态氮浓度;l1和ui分别为第i个决策变量的下界和上界;∆为超标惩罚项,计算公式为

其中,CNH和CNtot分别表示预测出水氨氮浓度超标值和预测出水总氮超标值;fNH和fNtot分别表示第1节建立的SNH,e预测模型和SNtot,e预测模型;4和18分别为国家规定的SNH,e和SNtot,e上限值.
2.3 种群稀疏度求取
本文实验初始种群总数N为100,即有N个解,首先对目标函数值进行归一化.设第i个解Xi的目标向量为(F1(Xi),F2(Xi)),则归一化公式为[18]
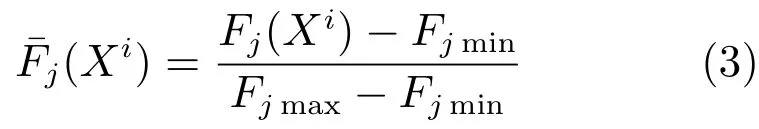
其中,Fjmin和Fjmax分别为当前所有解对应的第j个目标函数值的最大值和最小值.归一化后第i个解Xi的稀疏度计算公式为

其中,ni为目标函数空间中与目标向量F(Xi)欧氏距离小于r的其他目标向量的个数,r的取值范围为0 将当前稀疏度最小的非支配解X=(x1,x2)作为稀疏解,种群总数N为100,决策变量个数n为2.为了增加收敛精度,首先使用极限优化[19]变异方法进行局部搜索,产生局部解个数为n,产生局部解的变异公式为 其中,xi为决策变量;h为0~1的随机数;q为正实数,称为形状参数,本文将q设为11;βmax(xi)为当前决策变量xi可变动的最大值. 其次使用随机移民策略进行变异操作,增加收敛速度的同时避免陷入局部最优.该变异策略则产生局部解个数为种群总数的20%(如不能整除则取整),变异公式为 其中,γ为0~1.2的随机数.以上两种变异策略共产生n+d0.2Ne个局部解. 使用NSGA2-DLS[12]算法进行多目标优化.溶解氧浓度取值范围为[1.4,2.7],硝态氮浓度取值范围为[0.5,1.5].初始种群数量N为100,最大函数调用次数Imax为30,交叉概率0.9;变异概率0.01.形状参数q为11.具体优化步骤如下: 步骤1.在取值范围内随机初始化种群PI={X1,X2,···,XN},其中,. 步骤2.计算PI中所有解的适应度值和拥挤距离(与标准NSGA2相同),对PI中的解进行非支配排序,当前种群中所有非支配解记为PC. 步骤3.按照标准NSGA2算法对PI中的种群进行交叉变异,形成子代PM. 步骤4.在目标函数空间内,按式(3)和式(4)计算PC中所有解的稀疏度,选择稀疏度最小的解作为稀疏解X=(x1,x2). 步骤5.按式(5)~(10)形成n+d0.2Ne个局部解,所有局部解组成种群PN,PN参与到下一代的竞争中. 步骤6.将PI,PN和PM合并,并对所有解进行非支配排序和拥挤距离计算,从中选取最优的N个解形成下一代种群PO,并设PI=PO.PO的选取规则为:优先选取非支配解,当非支配解数量不足N时,选取次优解,以此类推,直到解的数量达到N为止;在同一等级的解中,拥挤距离大的解优先选取. 步骤7.重复步骤2~6,当达到最大迭代步数Imax时进行下一步. 步骤8.当前PI中的非支配解即为得到的最优解. 使用多目标优化算法得到多个非支配解,需要从中选取合适的解作为SO,5和SNO,2设定值.从非支配解集中选取解时,具体步骤如下: 步骤1.将得到的所有非支配解带入预测模型,将出水指标达标的解加入解集PD. 步骤2.若PD不为空集,则降低能耗为主要目标,从PD中选取能耗最低的解作为设定值. 步骤3.若PD为空集,则抑制出水污染浓度为主要目标,从非支配解中选取水质最高的解作为设定值. 该最优解选取方法将预测模型应用于最优解的选取过程,可以优先通过调节设定值确保出水水质达标,从而尽可能降低能耗. 根据第2节得到SO,5和SNO,2设定值,将设定值带入SNH,e和SNtot,e预测模型.如果预测出水水质达标则切换到跟踪控制策略,对SO,5和SNO,2进行跟踪控制.如果预测SNH,e或SNtot,e超标,则切换到抑制控制策略,对峰值进行抑制.控制策略图如图6所示. 当预测SNH,e和SNtot,e都不超标时,使用两个模糊控制器分别控制KLa,5和Qa,从而对SO,5和SNO,2进行跟踪控制. SO,5模糊跟踪控制器的输入为当前浓度与设定值之间的误差eo和4eo误差变化量,输出为KLa,5变化量4KLa,5.Ke,Kec和Ku分别为误差、误差变化量的量化因子和曝气变化量的比例因子,分别设为10,6,−20.eo和4KLa,5的基本论域为[−6,6],4eo的基本论域为[−4,4].eo和4KLa,5对应的模糊子集为:{NB,NM,NS,ZO,PS,PM,PB},分别表示负大,负中,负小,零,正小,正中,正大.4eo的模糊子集为:{NB,NS,ZO,PS,PB},分别表示负大,负小,零,正小,正大.eo和4eo的语言变量分别用E和EC表示,模糊控制器规则表如表3所示. 图6 决策优化控制示意图Fig.6 The proposed decision and optimization control system 表3 SO,5模糊跟踪控制器模糊规则Table 3 Fuzzy rules ofSO,5fuzzy controller SNO,2模糊跟踪控制器的输入为当前浓度与设定值之间的误差eNO和误差变化量4eNO,输出为Qa,对应的量化因子和比例因子分别为12,40和−2500.论域、模糊子集和模糊规则与SO,5跟踪控制器相同. 当预测SNH,e超标时,使用一个模糊控制器对Qa进行控制,从而抑制出水氨氮峰值.当预测出水氨氮超标时,首先增加Qa稀释流入第一分区的氨氮浓度;当氨氮浓度峰值到达第五分区时,减少Qa以增加水力停留时间,从而促进硝化反应.在调整Qa的同时,将第五分区溶解氧设定值设定为原来的1.5倍. 模糊控制器的输入为第五分区氨氮浓度(SNH,5),输出为Qa.输入和输出变量都包含三个模糊子集:{L,M,H}分别表示低、中和高.模糊规则如下: SNH,5的取值范围为3~4.1mg/l,Qa的取值范围为3000~200000m3/d.当预测出水氨氮达标并且SNH,5小于3.5mg/l时切换回模糊跟踪控制. 当预测SNtot,e超标时,根据SNtot,e预测值对第一分区外加碳源(qEC1)和第二分区外加碳源(qEC2)进行模糊控制,增加碳源可以促进反硝化作用,去除氮元素.模糊控制器的输入为出水总氮预测值(SNtot),输出为外加碳源量qEC.输入和输出变量都包含三个模糊子集:{L,M,H}分别表示低、中和高.模糊规则如下: SNtot的取值范围为17~19.5mg/l,qEC的取值范围为4~7m3/d,qEC1的最大值为5,若qEC<5,则qEC1=qEC,否则qEC1=5,qEC2=qEC−5.当预测出水总氮低于17mg/l并且第五分区总氮低于13.5mg/l时,切换回模糊跟踪控制. 本文主要做了两组实验,一组实验采用基于NSGA2-DLS的优化控制策略进行污水处理控制,结果与已有的优化控制方法对比,主要目的为验证NSGA2-DLS在解决污水处理优化问题方面的有效性.另一组实验采用本文提出的决策优化控制策略,结果与其他决策控制方法对比,验证本文提出的决策优化控制策略可以在抑制SNH,e和SNtot,e超标的基础上降低能耗.所有实验采用MATLAB10.0b软件进行仿真实验,实验平台为国际通用仿真平台BSM1. 污水处理后出水水质限制如表4所示,包括SNH,e,SNtot,e,固体悬浮物浓度TSS,5天生物需氧量BOD5和化学需氧量COD. 表4 出水水质限制Table 4 Effluent quality limits 本文使用的评价指标主要有:水质EQ、总费用OCI和水质超标时间百分比P,具体公式为 其中,T为观察周期,SNKj为凯氏氮浓度,SNO为硝态氮浓度,Qe为出水流量. 其中,AE为曝气能耗,PE为泵送能耗,EC为碳源费用,计算公式为 其中,KLa,k为第k个池子氧转换系数,Vk为系数. 其中,Qa为内回流速,Qr为外回流速,Qw为污泥流速. 其中,qEC,k为第k个池子的外加碳源流速. 水质超标时间百分比计算公式为 其中,Tc为水质超标总时间,Tz为总运行时间. 为验证本文使用优化控制方法的有效性,使用基于NSGA2-DLS的优化控制方法对BSM1污水处理模型进行控制,但不对超标峰值进行抑制,模拟在晴天天气下连续进行7天优化控制.首先使用优化算法对SO,5和SNO,2设定值进行优化,由于污水处理是一个慢过程,控制需要一定的反应时间,因此每2小时优化一次设定值.然后使用模糊控制器对设定值进行跟踪控制. 各出水指标变化曲线如图7所示,SO,5和SNO,2设定值变化及跟踪效果如图8和图9所示.控制效果如表5所示,控制效果与固定设定值(SO,5和SNO,2设定值分别为2和1),不抑制峰值(记为F1),DPSO[20],APSO[21]和ESN[22]进行对比.从图7可以看出,出水TSS,BOD5和COD浓度均保持在规定范围以内,出水SNH和SNtot浓度虽然大部分时间在要求范围以内,但在峰值处超标严重.从图8和图9可以看出,本文使用的模糊控制器虽然可以有效跟踪设定值,但是在设定值变化时有超调,但此问题不是本文研究的重点.表5给出了不同优化控制方法对BSM1模型的控制效果,从表5可以看出,各出水指标均值都在限定范围之内,本文使用的NSGA2-DLS算法得到的能耗最低,但水质指标也有所升高. 图7 各出水水质浓度变化曲线Fig.7 The change of water quality parameters 通过以上分析可知,NSGA2-DLS算法在污水处理优化控制中的应用可以有效降低能耗,各指标均值都达到出水标准,但是SNH,e和SNtot,e峰值超标严重,峰值的抑制控制十分必要. 将优化控制与决策控制相结合,使用优化控制降低能耗,决策控制对SNH,e和SNtot,e峰值进行抑制,模拟在晴天天气下连续进行7天决策优化控制.首先使用优化算法对SO,5和SNO,2设定值进行优化,优化周期为2小时.然后使用预测模型预测SNH,e和SNtot,e是否超标,如果都不超标,则对SO,5和SNO,2进行跟踪控制;如预测SNH,e超标,则切换到SNH,e峰值抑制控制);如预测SNtot,e超标,则切换到SNtot,e峰值抑制控制. 表5 不同算法控制效果比较(出水指标、能耗和水质)Table 5 Performance comparison for different control algorithms(effluent parameters,OCIandEQ) 图8 SNO,2设定值及跟踪曲线Fig.8 Optimization and tracking results ofSNO,2 图9 SO,5设定值及跟踪曲线Fig.9 Optimization and tracking results ofSO,5 决策优化控制的出水TSS,BOD5和COD浓度变化如图10所示.决策优化控制与NSGA2-DLS优化控制下SNH,e和SNtot,e的对比如图11和图12所示.SO,5和SNO,2设定值变化及跟踪效果如图13和图14所示,Qa和KLa,5变化曲线如图15和图16所示.实验结果与其他抑制SNH,e和SNtot,e峰值方法进行比较,对比方法有:固定SO,5和SNO,2设定值抑制峰值 (记为 F2)、Jeppsson[23]、Nopens[24]、Flores-Alsina[25]和 Sant´ın[10],对比结果如表6所示. 表6 不同SNH,e和SNtot,e峰值抑制方法效果对比Table 6 Performance comparison for differentSNH,eandSNtot,epeak suppression methods 从图10可知,决策优化控制下出水TSS,BOD5和COD浓度均保持在规定范围以内.图11和图12表明,抑制控制的加入有效抑制了SNH,e和SNtot,e峰值.从图13和图14的SO,5和SNO,2跟踪曲线可以看出,当切换到抑制控制时,抑制峰值为首要目标,因此在抑制控制时SO,5和SNO,2与设定值相差较大.图15和图16表示的Qa变化曲线和KLa,5变化曲线显示了SNH,e和SNtot,e在预测达标和超标两种情况下,决策优化控制对Qa和KLa,5的控制.从表6的对比结果可以看出,本文提出的决策优化控制方法可以有效抑制SNH,e和SNtot,e峰值,出水SNH,e和SNtot,e始终保持在规定范围以内,超标时间百分比均为0%.其他抑制峰值方法均不能保持出水SNH,e和SNtot,e始终达标.与其他方法相比,决策优化控制消耗的能耗明显降低,虽然水质指标高于其他方法,但污水控制目标为在出水达标的情况下尽可能降低能耗,因此本文提出的决策优化控制节能降耗效果优于所对比控制方法,实现了在抑制SNH,e和SNtot,e峰值的情况下降低能耗的目标. 图10 出水TSS、BOD5和COD浓度变化曲线Fig.10 The curves of TSS,BOD5and COD of effluent 本文提出的决策优化控制将决策控制与优化控制相结合,在抑制出水氨氮和总氮浓度峰值的情况下降低能耗.理论分析与实验结果表明,决策优化控制在以下方面对污水处理控制做出了贡献. 图11 决策优化控制与优化控制SNH,e变化曲线Fig.11 The curves ofSNH,ewith decision and optimization control system and optimization control system 图12 决策优化控制与优化控制SNtot,e变化曲线Fig.12 The curves ofSNtot,ewith decision and optimization control system and optimization control system 图13SO,5设定值及跟踪曲线Fig.13 Optimization and tracking results ofSO,5 1)在预测模型建立方面,本文提出的时滞时间计算方法对建模数据采样提供了新思路;将第二分区溶解氧浓度和第五分区硝态氮浓度作为预测模型输入变量提高了模型的精度. 虽然决策优化控制取得了较好的效果,但仍然有一些方面需要改进,决策优化控制使用的模糊控制器跟踪性能一般,在设定值变化时超调严重;本文使用多层感知器进行建模,可以在权值初始化、权值调整算法等方面进行改进,提高建模精度,也可以尝试其他建模方法. 图14 SNO,2设定值及跟踪曲线Fig.14 Optimization and tracking results ofSNO,2 图15 Qa变化曲线Fig.15 The curve ofQa 图16 KLa,5变化曲线Fig.16 The curve ofKLa,5 2)将NSGA2-DLS优化算法应用于设定值优化环节,提高了优化解的质量,降低了能耗. 3)在优化过程和最优解选取过程中引入预测模型,将优化控制与决策控制有效结合,实验结果显示,决策优化控制可以有效抑制SNH,e和SNtot,e峰值,与其他抑制控制相比,决策优化控制的能耗更低,达到了出水达标的情况下节能降耗的目的.2.4 局部搜索过程


2.5 多目标优化步骤
2.6 最优解选取
3 决策优化控制
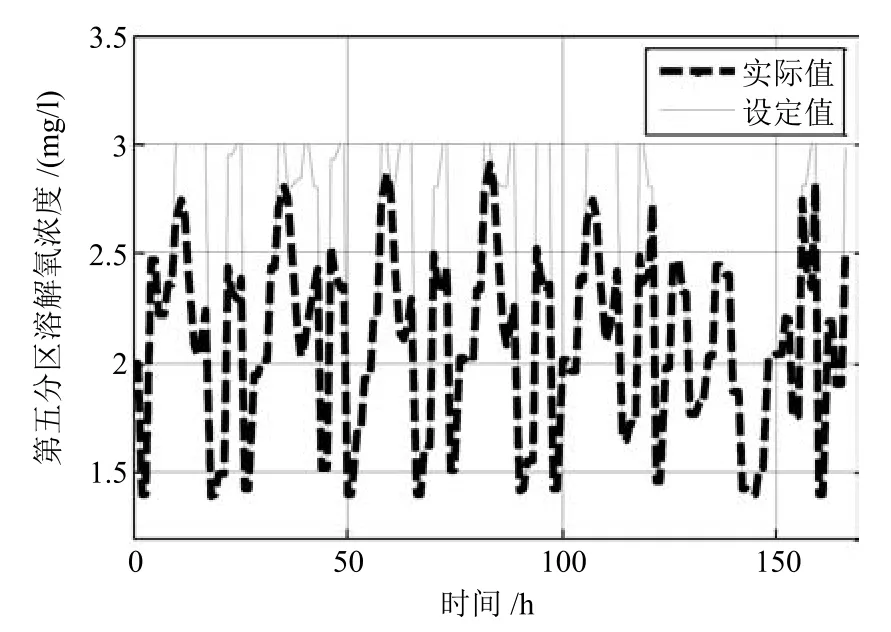
3.1 溶解氧、硝态氮浓度跟踪控制
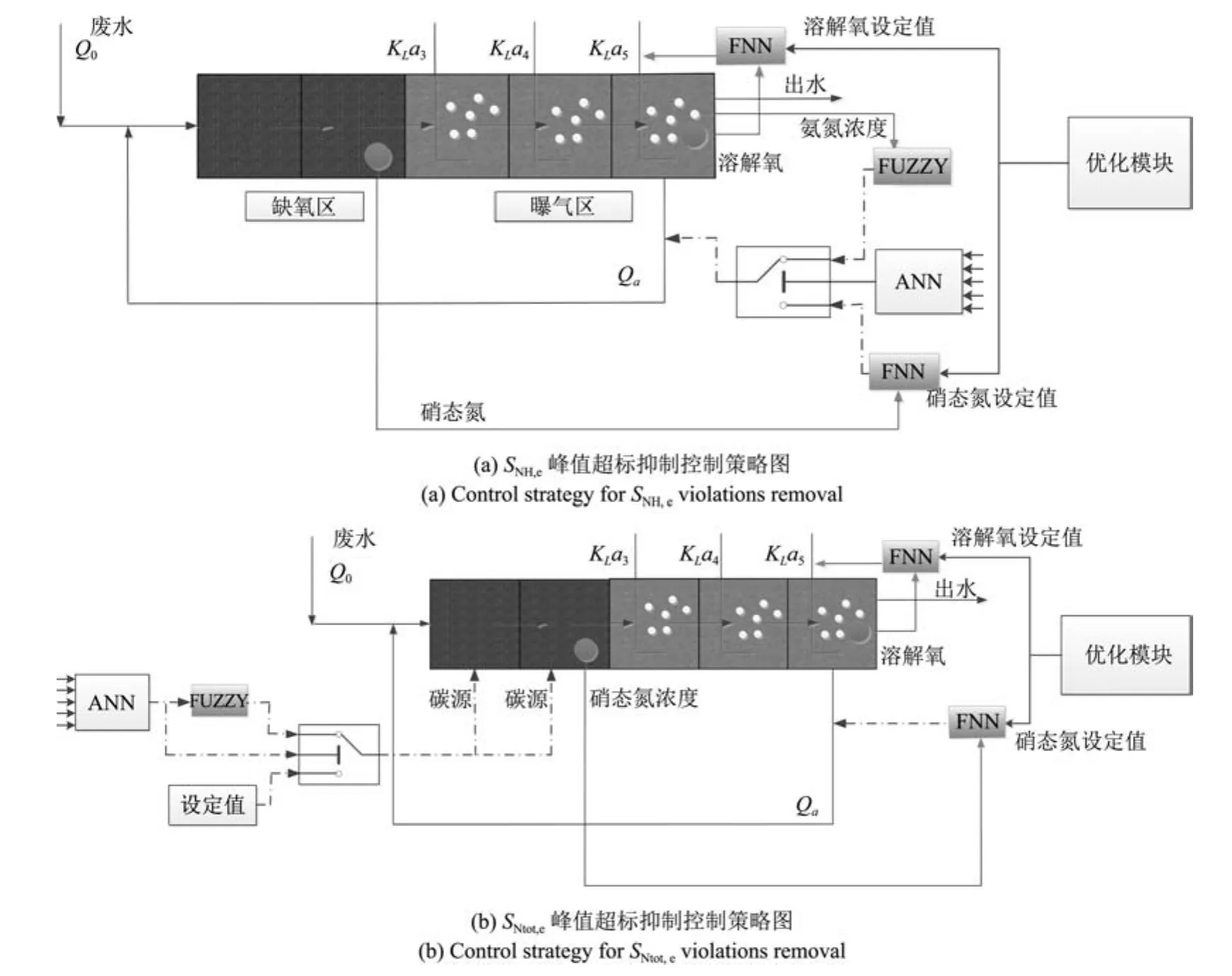

3.2 出水氨氮浓度峰值抑制控制

3.3 出水总氮浓度峰值抑制控制

4 实验结果及分析
4.1 评价指标







4.2 基于NSGA2-DLS的优化控制

4.3 决策优化控制





5 总结与展望