基于RISE反馈的串联弹性驱动器最优控制方法

孙雷 孙伟超 王萌 刘景泰

近年来,采用串联弹性驱动器(Series elastic actuator,SEA)的柔性关节机器人由于具有良好的柔顺性和安全交互能力而得到关注.SEA是一种将弹性组件串联于电机和负载之间的柔性驱动器,弹性组件的引入,使得机器人的输出呈现被动柔性,进而确保机器人与环境和人能够进行安全的物理接触.另外,弹性组件的形变量与输出力矩呈对应关系,通过对弹性组件的测量与控制可以使系统具有高精度的力/力矩输出.基于以上优点,串联弹性驱动器可以被当做理想力源应用于机器人交互系统[1−5].

针对SEA的力/力矩控制问题,国内外研究学者已经提出了很多控制策略.首先,Pratt等在提出SEA概念的时候提出了一种前馈补偿与PID反馈相结合的控制策略[6].随后,Pratt等又提出了级联PID控制方法[7],其中位置控制和力矩控制分别作为控制的内外环.之后,很多改进的级联PID控制策略相继被提出[8−10].由于结构简单,便于应用,级联PID控制方法目前被广泛应用于SEA的力/力矩控制[1,11].为了提升系统的鲁棒性,Kong等[12−13]提出了基于线性扰动观测器(Linear disturbance observer,LDOB)的控制方法;Yoo等[14]提出了基于内部补偿器(Robust internal-loop compensator,RIC)的控制方法,其原理类似于LDOB.除此之外,一系列先进控制策略,例如自适应控制[15]、滑模控制[16]、H2最优控制[17]、神经网络[18]等,也都被应用于SEA的控制问题上,并取得了不错的效果.

值得指出的是,包括上述列举的方法在内,已有的绝大多数SEA力/力矩控制方法都是针对线性SEA模型,即SEA的输出力矩与电机和负载端的相对转角呈线性关系.然而,一些非线性SEA具有更高的能量密度和仿生特性,其力/力矩输出与电机和负载的相对转角呈现非线性关系,在一些文献中,该类驱动器也被称作Variable stiffness/impedance actuator(VSA/VIA)[19−21].显然,非线性SEA 的力/力矩控制问题更具挑战性,目前该方面的研究相对较少.文献[22−25]应用级联PID控制方法来控制非线性SEA,对于复杂模型来说,PID控制是一种简单有效的控制方法,但该方法缺少理论分析;文献[24−25]提出一种模型线性化的方法,将表示SEA力矩输出特性的非线性函数进行局部线性化,之后再利用线性系统理论分别设计LDOB和控制器使系统稳定,但是该控制方法最大的不足在于只能确保系统在局部稳定;文献[26−27]分别针对投掷和敲击任务,提出了基于最优控制理论的控制方法,该方法在分析过程中假定负载端的动力学模型已知,所以无法应对在碰撞等交互应用中负载端动力学模型剧烈变化的情况;文献[28−29]提出了一种基于延时估计的控制方法,但该类方法只能保证控制误差全局最终一致有界(Globally,uniformly,ultimately bounded,GUUB);文献[30]提出了一种基于非线性扰动观测器(Nonlinear disturbance observer,NDOB)的滑模控制方法,但该方法对SEA动力学建模中潜在的内外扰动缺乏有效分析.

考虑到上述问题,本文提出一种基于RISE(Robust integral of the sign of the error)反馈的最优控制方法,保证在存在模型参数不确定和有界扰动的情况下,SEA的输出力矩在交互过程中能够快速达到期望值.具体来说,首先对SEA的模型进行分析和变换;然后假设模型参数和扰动均已知,并在此基础上基于HJB最优控制理论设计最优控制律;之后基于RISE反馈重新设计控制器抵消模型参数不确定性和有界扰动,基于Lyapunov理论分析控制器的收敛性和信号的有界性;最后与级联PID的控制性能进行实验对比.

本文的其他部分组织如下:第1节通过对SEA的动力学模型进行分析和变换,对其控制问题进行详尽描述;第2节假设系统模型完全已知,并在此基础上设计最优控制律;第3节基于RISE反馈来修正控制输入,使得模型的不确定项能被抵消掉;第4节稳定性和信号有界性分析;第5节给出与级联PID的实验对比结果,验证算法的有效性;第6节是对本文主要工作的总结和展望.

1 问题描述

本文的研究对象为旋转型非线性SEA,即SEA的输出力矩与转角差之间呈非线性关系.模型如下:

其中,θM和θL分别表示电机端和负载端的转角,ϕ表示电机端和负载端的转角差,JM和JL分别表示电机端和负载端的转动惯量,cM和cL分别表示电机端和负载端的科氏力等因素,τSEA表示SEA的输出力矩,与ϕ呈非线性关系,q1(t)和q2(t)分别表示电机端和负载端的未建模项、参数摄动项和扰动项,有界且其各阶导数也有界,τ表示控制输入,如图1所示.

图1 SEA示意图Fig.1 Structure of SEA

控制任务为:存在模型参数不确定和有界扰动时,设计合适的控制器,使得τSEA→τSEA,d.为此,做如下合理假设:

假设1.τSEA与ϕ之间为一一对应的映射关系,对应关系f有界,且f的导数也有界;

假设2.期望力矩及其1,2,3,4阶导数均有界.

由于输出力矩与转角差一一对应,因此有ϕd=f−1(τSEA,d),进而有

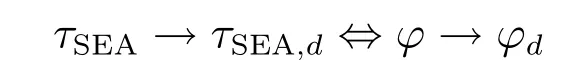
基于以上分析,可将力矩控制和跟踪问题转化为转角差的控制和跟踪问题.因此相应地将模型变化为如下形式:

在实际交互场景中,负载端模型中的JL和cL等参数会发生不确定性变化,上述变换后的模型不包括负载端信息,可以从理论上消除负载端模型的不确定性对于系统的影响.不论负载端如何变化,控制任务始终是ϕ→ϕd(τSEA→ τSEA,d).上述模型中的集总扰动项d(t)包括负载的速度和加速度、模型误差等信息,弹性元件的引入使系统呈现出低阻抗和能量缓冲特性,这使得在实际物理交互过程中,扰动项的变化并非瞬间完成,尤其是在人机交互过程中,交互产生的扰动的频率及幅值都相对较小,因此对于扰动项有以下说明:

假设3.集总扰动项d(t)及其1阶和2阶变化率均有界.

综上,控制问题描述为:针对系统(3),设计合适的控制律,使得系统能在克服扰动项d(t)的同时实现ϕ→ϕd.

2 最优控制律设计

前面的分析已将力矩跟踪转化为转角差跟踪,因此定义跟踪误差e1及辅助变量e2为

其中,α1为待计算的正常数.

其中,α2为正常数.

将控制误差变换为状态空间表达式.由式(3)～(5)可得

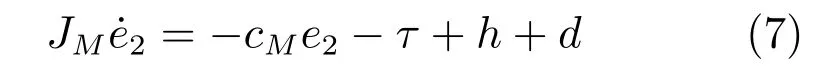
其中,

暂时假设动态模型(3)中各项均已知,设计控制律如下:

则有

结合式(5)和式(10)有

在此基础上,引入二次型控制指标

其中,Q>0,R>0.控制问题转化为设计u使得J(u)最小,记最优控制律为u∗(t).上述指标不包含重力及扰动项,因为在实际中很难获得这些项.

上述最优控制问题有解,即u∗(t)存在的充要条件是存在V=V(z,t)满足HJB方程[31]

其中,

而

可以证明

满足上述HJB方程,其中,K为待计算的参数.证明如下:

由于u无约束,因此取最小值时,有

将式(11),(14)和(15)代入上式,得

解得

对哈密顿函数求二次偏导,可知

即哈密顿函数关于u的一阶偏导单调递增,进而可知u∗是其最小值点.另外值得注意的是,被控对象为多关节SEA,仍然有此结论,推导过程类似.

从上述推导过程可以看出,V(z,t)的存在性依赖于式(13)有解,即矩阵P需存在,下面证明P应满足的条件和其存在性.

由式(13)可得

联立L(z,u)的表达式和式(11),(15),(21),可得

由上式知,若矩阵P为代数里卡蒂方程的解,则其满足式(23).将A,B,P,Q的表达式代入上式,得

上述矩阵方程意味着,矩阵Q半正定的前提下,应有

显然存在这样的参数.因此,当式(25)得到满足时,式(19)所示的控制律能使式(12)中的J(u)最小.

3 基于RISE反馈的控制输入修正

上一节中的控制律(19)能使式(12)达到最小,但是式(9)中,τ的表达式中d是未知的,因此控制律(9)无法直接应用.因此做如下修正:

由式(6)和式(7),可得

设计控制输入

代入式(26),得

其中,

对式(28)求导,得

其中,

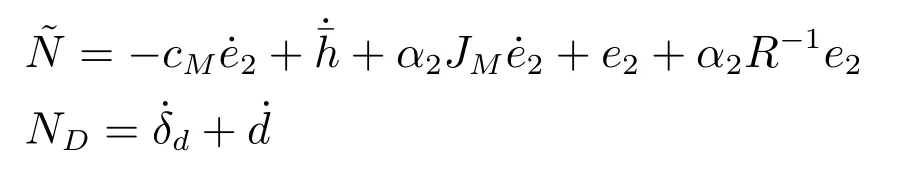
其中,

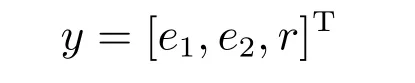
控制输入修正部分为

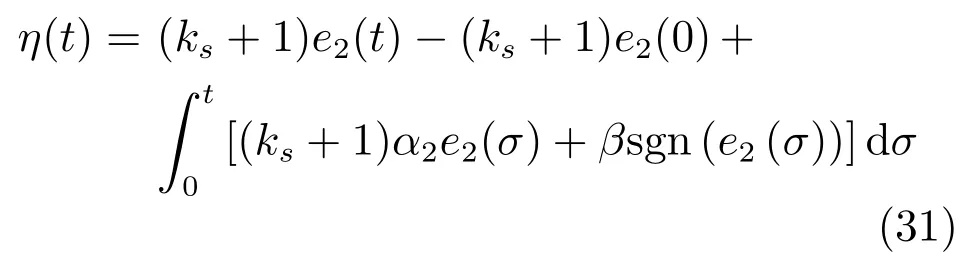
其中,sgn(·)表示符号函数,β满足

ks为正常数控制增益.将上式代入式(29),可得闭环系统的动态方程为

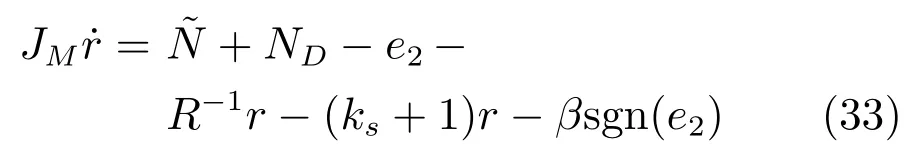
4 稳定性分析

可以证明,式(19),(27)和(31)构成的控制输入可以使

同时,控制输入有界.证明如下:

首先引入辅助变量L(t)为

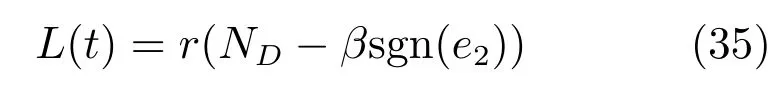
则有

定义

定义向量

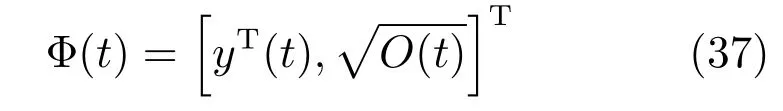
选取Lyapunov候选函数为

则有

对Lyapunov候选函数求导,可得

其中,λ3=min{2α1−1,α2−1,1+R−1}.

为保证λ3为正数,要求

为保证U(Φ)半正定,即常数c>0,则应有kyk.为此,定义区域

于是,当Φ∈D时,VL(Φ,t)∈L∞,进而推得e1(t)∈L∞,e2(t)∈L∞,r(t)∈L∞.由式(5)和式(6)可知1(t)∈L∞,2(t)∈L∞;由式(4),(5)和(6)可知ϕ∈L∞,,∈L∞;由式(3)可知τ∈L∞;由式(19)可知u∈L∞,进而∈L∞且η∈L∞;由式(31)可得∈L∞;由式(9)可知h∈L∞;由式(8)可计算得∈L∞;由式(33)可知.所以U(Φ)在D上一致连续.

定义区域

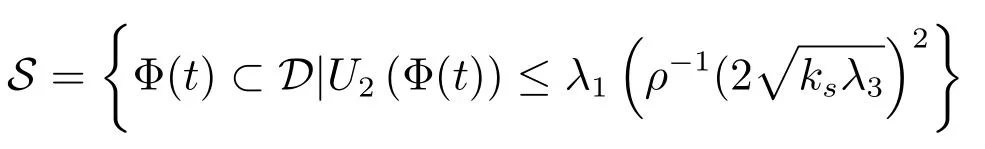
由类不变定理可知

则∀y(0)∈S,有

则由e2(t)和r(t)的定义式可知

由式(19)可知

进而由式(26)可知

可以调整ks的值,使得y(0)∈S.

综上所述,即使存在模型参数不确定和未知有界扰动,由式(19),(27)和(31)构成的控制输入,当其参数满足式(25),(32)和(40)的约束时,能够实现最优控制且跟踪误差以及跟踪误差的1阶和2阶导数都渐近收敛至0.

5 实验验证

本文整合了最优控制原理与RISE控制策略,其中RISE方法具有辨识系统未知模型并且消除系统扰动的作用,在上面分析中使用李雅普诺夫方法证明了RISE反馈能够渐近辨识系统未知项和扰动项,从理论上证明了系统控制律最终精确收敛到最优控制律.下面用一组仿真实验来验证系统存在扰动时控制策略的最优性.在SEA系统中加入扰动d(t)=0.1+0.5sin(2πt)之后进行阶跃信号响应测试,图2是阶跃信号跟随情况,图3是RISE反馈项与实际的h(t)+d(t)的对比结果.仿真结果中RISE反馈项能够有效修正h(t)+d(t),误差收敛于零.验证了最终控制律会收敛于最优控制律,系统在考虑了不确定干扰之后仍具有最优性.

图2 阶跃信号仿真结果Fig.2 Simulink result of step signal

为了进一步验证本文方法的有效性,本节在自主搭建的单关节SEA平台上进行实验验证.

如图4所示,本文的SEA系统由Maxon直流伺服电机驱动(减速比N=100:1),电机端安装增量式编码器(4000PPR),负载端安装有绝对值编码器(4096PPR).弹性装置安装在电机与负载之间,弹性主要有三个压簧提供.当电机与负载发生相对转动时,滚轮会沿着圆弧轨道运动,压缩三个弹簧,弹簧的压缩会对负载产生力矩,详见图5.

根据图5,该SEA系统的输出力矩和相对转角的关系如下:

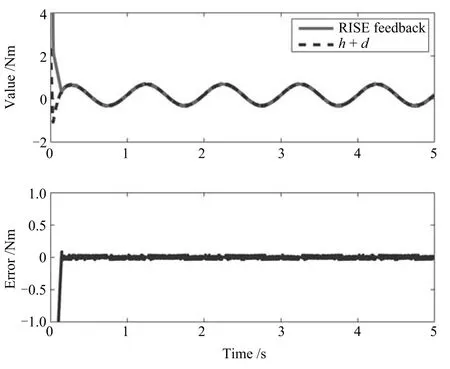
图3 RISE反馈项与实际未知项对比结果Fig.3 Comparison result of RISE feedback term with disturbance term

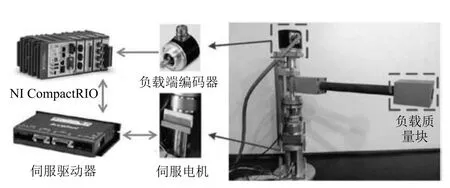
图4 SEA实验平台Fig.4 SEA testbed

图5 SEA弹性结构Fig.5 Elastic structure of SEA

由此可得SEA输出力矩与转角差的关系为

式中,θ表示滚轮在圆弧轨道滚动的角度;R,r分别表示圆弧轨道和滚轮的半径;∆y表示弹簧的压缩量;F表示三个弹簧压缩产生的合力.该模型的正确性已经在文献[32]中得到实验验证,为SEA力矩控制打下了基础.

为了体现本文方法的有效性,在实验时与文献[20]中的级联PID控制方法进行了比较(级联PID控制方法作为一种简单有效的输出反馈控制策略,被广泛用于SEA的力矩控制中).本文应用的SEA相关机械参数如表1所示,实验采用NI CompactRIO控制器,控制周期1ms,经过调节,本文设计的控制器参数为α1=30,α2=5,β=20,ks=5;级联PID力矩控制参数为kop=10,koi=3,kod=0.5,速度环控制参数为kip=3,kii=1,kid=0.

表1 SEA机械参数Table 1 Mechanical parameter of SEA

实验1.环境交互模拟

在本组试验中,模拟串联弹性驱动器负载端与环境交互的情形,与传统的级联PID控制策略进行了实验对比.具体操作如下:负载在初始时刻被挡板挡住,之后输入阶跃信号,待负载稳定后撤去挡板,负载在SEA驱动下短暂运动一段时间后与另一挡板发生碰撞.通过分析可以发现,在挡板没被撤掉之前的过程可以看作系统对阶跃信号的调节控制,系统集总扰动项d(t)未知,可用来验证存在模型不确定情况下的系统的响应能力.在之后的释放和碰撞过程中,负载端动力学模型中的JL,cL等参数会发生两次突变,系统模型发生不确定性变化,可用来描述SEA与环境发生物理交互时的情形.

在t=0s时输入幅值为0.2rad的阶跃信号,从实验结果图6可以看出,在阶跃响应阶段,本文提出的控制策略调节时间为0.2s,超调量约为4%,级联PID控制策略调节时间约为0.4s,超调量约为20%,本文控制方法较级联PID控制策略收敛速度更快,且超调较小.在释放与碰撞阶段,面对相同扰动时,本文方法输出波动较小,能够更快地恢复到期望值;而级联PID控制策略控制器性能明显下降,SEA输出力矩波动明显且需要较长的时间才能恢复到期望值.本组实验充分说明了本文方法能够更好地应对存在模型不确定性与环境交互时负载端模型剧烈变化的情况,拥有更强的鲁棒性,更适用于交互式机器人系统.

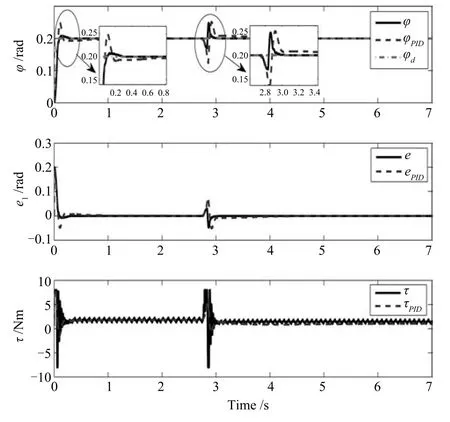
图6 环境交互实验结果Fig.6 Experiment result of robotenvironment-interaction

实验2.人机交互模拟

在人机交互情景中,零阻抗控制常用来评价控制器的性能指标,在本组试验中采用零阻抗控制来模拟人机交互.在实验过程中,驱动器输出力矩设定为零,人手持负载做无规则往复运动,控制策略的性能表现为电机对负载的跟随效果.

从实验结果可以看出,负载跟随人做无规则往复运动时,电机能够有效地跟随负载,跟随误差约为0.01rad,转角差ϕ被控制在很小的范围内,对应SEA输出力矩很小,并且输入较为平滑合理,表现出控制系统对于误差和输入的优化.图7和图8是负载与人交互时的运动情况与电机的跟随效果.实验结果表明,本文提出的控制方法具有良好的顺应性与低阻抗特性,在实际SEA交互系统中具有良好的应用价值.

6 结论

针对SEA的力矩控制问题,本文提出一种基于RISE反馈的最优控制策略.首先假设系统模型参数和扰动均已知,在此基础上基于最优控制理论设计最优控制律,之后基于RISE反馈对控制律进行修正,文中对跟踪误差的收敛性及信号的有界性进行了严格的数学分析.通过仿真实验验证了RISE反馈项能够渐近辨识模型未知参数和有界扰动,系统控制律最终收敛到最优控制律,算法在存在未知扰动情况下仍具有最优性.最后通过环境交互实验与人机交互实验,验证了算法在实际平台上的有效性.在接下来的工作中,我们将对多关节SEA机器人的力矩控制问题及其应用展开研究.

图7 电机与负载运动情况Fig.7 Motion result of motor and load

图8 人机交互实验结果Fig.8 Experiment result of human-robot-interaction