初中数学教学中反例的运用

熊俊伟

（江西省宜春市经都学校 江西宜春 336000）

引言

在平时的教学中，我们经常会遇到一些使我们感到困惑的问题。此时，我们需要发挥人脑思维的作用。如果我们不能从正面求出，为什么不试着从反面求出呢?反例教学可以引发学生的思维，使学生愿意去思索。[1]

一、在概念教学中反例的运用

初中数学教学应该通过运用反例来解释基本知识，使学生能够区分容易产生的混沌和错误，从而更加牢固。[2]

案例一：（1）在人教版七年级上册第一章第二节“数轴、相反数与绝对值” 的教学中，数轴的概念为规定了原点、正方向和单位长度的直线叫做数轴。可以列举以下反例来加深学生对数轴概念的理解。

如下所示，下列所表示的都不是数轴。

由以上反例知，数轴的三要素为：原点、正方向和单位长度。数轴是直线，而不是射线或线段。

（2）在人教版七年级下册无理数的教学中，无理数的概念为无限不循环小数叫做无理数。例如，等都是无理数，π=3.14159265···学生常会错误理解为：无限小数或带根号的数都是无理数。

下面举出反例：

3.14不是无理数，无限循环小数是有理数；

（3）在人教版八年级上册第十五章第三节“分式方程”的教学中，分式方程的概念：分母中含有未知数的方程叫做分式方程。

下列方程不是分式方程：

（4）在人教版七年级下册“平行线”的教学中，平行线概念的错误理解：在同一平面内不相交的线是平行线。

下列不是平行线：

（正确的理解是在同一平面内不相交的直线是平行线。）

二、在平面几何证明中反例的运用

在教学过程中，可以使用一些证明问题来检验逻辑是不是严格，并通过反例来否定不正确的证据，以便人们可以不断摸索和发掘正确的方法和结论。

案例二：人教版八年级下册的教学中，平行四边形的条件：证若四边形一组对边及一组对角相等，则是平行四边形。

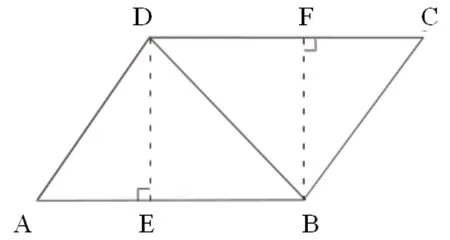
图1

证明：如图1，设四边形ABCD中，AD=BC，∠BAD=∠DCB。

作DE⊥AB，BF⊥DC，则Rt△ADE ≌ Rt△CBF（斜边一锐角相等）

∴DE=EF（对应边），Rt△DEB ≌ Rt△BFD（斜边一股相等）

∴EF=DF，∴AB=DC（∵AE=FC）

∴ABCD是平行四边形

图2

分析：若四边形一组对边及一组对角相等，这四边形不一定是平行四边形。其实自四边形一顶点作对边的垂线，垂足可能是在对边的延长线上。如图 2，AD=BC，∠BAD=∠DCB，但自 B 作DC 的垂线，虽然仍可证得 AE=FC，EB=FD，但AB=AE + EB，DC=FC－FD，并不相等。原证没有考虑这种情形，所以结论是错误的。

由上可以看出，反例对于证明的作用是相当重要的。

三、用反例否定错误推理

案例三：例1 判断下列推理的正误：

（错误，在b≠0时才成立，b=0时，0没有倒数。）

（错误，当 a 是负数时，不等式两边同除以一个负数不等号方向会改变。）

例2要证明“两个无理数的积仍是无理数”这一命题是否为真命题时，为无理数，则此命题为真。

面对这样的问题，我们应尝试着举出反例，若为有理数，此命题为假命题。像这样，我们可以通过给出一个反例验证真假。

四、反例的运用应注意的问题

1.反例的举例要有意义

毫无目的的反例就没有意义可言。针对课本的教学内容，针对性地提出反例，合理地进行教学设计。针对问题的难易程度，有计划地运用重点和难点。

2.运用反例的时间

什么时候使用反例，使用的基础是什么，这就是老师在使用反例前需要考虑的事情。在教学过程中运用反例是为了达到画龙点睛的效果。因此，教师应认识到反例的使用只是一种辅助的手段，而不是一种唯一的手段。

3.运用反例时要师生互动

教师的辅助功能主要反映在指导方面上，有效的指导有助于学生独立学习知识。对于反例的应用，有很多优点，可以从另一个角度来检验数学知识是否正确。然而，只有学生听的反例教学，并不符合培养学生自主学习能力的初志。因此，教师应该在辅助学生之后给他们上课，以便他们可以提出自己的反例。

4.运用反例时避免分散注意力

在反例和正例同时出现的情况下，应避免反例分散学生的注意力。如果稍不注意，学生重点记忆反知识，导致学生认为正确的知识是错误的，进而使大脑记下反例，很难纠正。因此，在反例教学中，教师应避免分散学生的注意力。

结语

反例教学在课堂上起着一定的引导和调节作用，它还可以培养学生思维的严谨性和综合性。此外，教师应认识到反例的使用只是一种辅助的手段，而不是一种唯一的手段。