化归方法及其应用
计 军
(辽宁省彰武县满堂红九年制学校 辽宁阜新 123200)
数学在其漫长的发展过程中,不仅构建了严密的思想体系,而且形成了一套行之有效的思想方法,划归思想就是常用的方法之一。
一、化归原则
人们在研究和运用数学的长期实践中,获得了大量的成果,也积累了丰富的经验,许多问题的解决也形成了固定的方法模式和约定俗成的步骤。人们把这种有既定解决方法和程序的问题叫做规范化或称为化归,化归就是运用某种方法和手段把有待解决的较为生疏较为复杂问题归结为所熟悉的规范性问题来解决的方法。[1]
例如,对于一元二次方程,人们已经掌握了求根公式,因而求解一元二次方程的问题是规范问题,而把分式方程、无理方程通过换元等方法转化为一元二次方程就是问题的规范化。其中换元是实现规范化的手段,具有转化归结的作用,可以称这为化归的方法。
规范问题具有确定性,相对性和发展性的特征。对于规范问题,人们不但可以运用书籍的理论和技术达成问题的解决,而且已经掌握了固定的步骤和程序,这就是确定性,所谓相对性,是指对于数学研究工作者以及不同层次的学习者,规范问题的范围并不相同。例如建于高中生和初中生而言,对于初中生不是规范性问题对于高中生就可以看作规范性问题,随着个人数学知识的增长,规范问题也在不断扩大,因此规范问题又具有发展性。[2]
化归原则的核心是实现问题的规范化。也就是把一个生疏的、复杂的问题化为熟悉的、简单的问题,以便利用已知的理论、方法和程序实现问题的解决,它的结构图如下所示。由此不难看出,熟悉化和简单化是化归的基本方向。
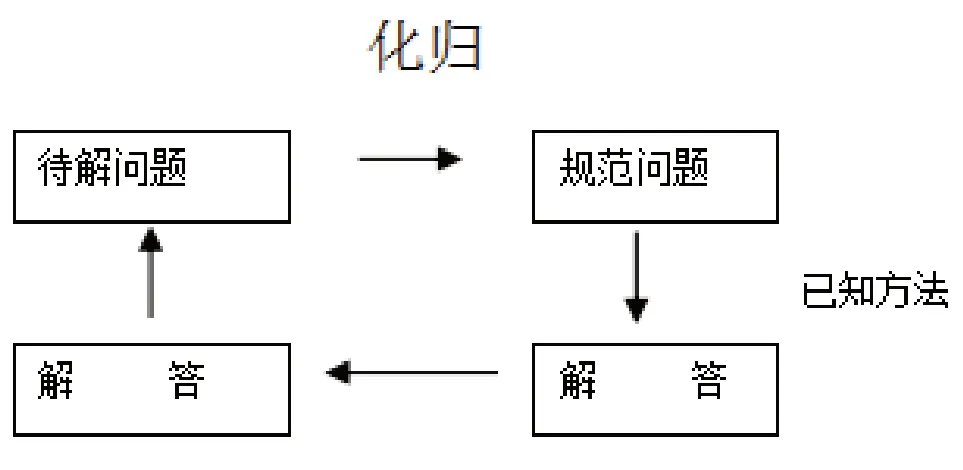
二、化归原则的基本思想
化归原则的结构中蕴涵着三个基本要素,即化归的对象,目标和方法,化归的对象就上待解问题中需要变更的成分,化规的目标是指所要达到的规范问题。所谓化归的方法,就是规范化的手段,措施和技术。例如对于初中生而言解二元一次方程组,一般要化为一元一次方程,这里二元一次方程线是化归对象,一元一次方程是化归的目标,而把二元一次方程组化为一元一阅人多矣次方程所用带入法或加减法就是化归的方法,在化归的三要素中,化归应选是实现化归的关键,这是显而易见的。唯物辩证法指出,客观事物是发展变化的,不同事物间存在着种种联系,各种矛盾无不在一定的条件下互相转化,化归正式人们对这种联系和转化的一种能动的反映。从哲学的高度看,化归原则着眼于提示矛盾实现转化,在迁移转化中达到问题的规范化。因此,化归原则裨上是转化矛盾的原则,它的“运动-转化-解决矛盾”的基本思想具有深刻的辨证性质。
三、化归原则中,实现化归的方法是多样的
按照应用范围的广度来划分,数学中的化归方法分为三类,就是多维化归方法,二维化归方法和单维化归方法。
1.多维化归方法,就是跨越多种数学分支,广泛适用于数学各学科的化归,归方法。例如,换元方法,恒等变换法、反证法、构造法、待定系数法、数学归纳法等,它们既适用于几何、三角等初等数学的各个分支,又适用于高等数学的各个分学科,其应用十分广泛,因而属于多维化归方法。
2.二维化归方法,这是指沟通两个不同数学分支学科的化归方法,是两个分支学科之间的转化。例如,解析法、三角带换法等都可以沟通两个数学分支学科,以便发挥两个学科的理论和方法的优势实现问题的解决,因而都是二维化归方法。
3.单维化归方法,这是只适用于某一学科的化归方法。是本学科系统内部的转化。例如,代入法、加减法、判断式法、坐标变换法等都是单维化归方法。[3]
例1: 如图,菱形ABCD中,AB=2、∠BAD=60°,E是AB的中点,P是对角线AC上任一动点,则PE+PB的最小值是多少?
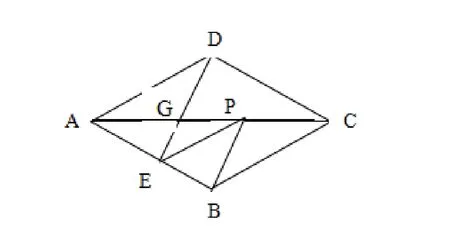
分析:求PE+PB的最小值问题可以转化为“求作线段AC上一点G,使G到已知点E、B的距离之和最短”的问题,这个简单问题被放到菱形中去,自然的想到菱形是轴对称图形,我们只要连接E和B关于AC的对称点D,则线段DE与AC的交点G,就是线段AC上到点E、B的距离和最笑的点,由于GB=GD,所以GB+GE=DE在等边△AB D中,易求出DE=,故PE+PB最小值为。
例2:解方程组 2X-Y+Z=-1 ①
X+3Y-2Z=-5 ②
4X-3Y-5Z=7 ③
分析这是一个三元一次方程组,考虑先化为二元一次方程组,再化为一元一次方程组,具体方法为 ②+③得5X-7Z=2④
①X3得+②得7X+Z=-8⑤
得二元一次方程组 5X-7Z=2 ④
7X+Z=-8 ⑤
第一次化归完成,再由⑤得Z=-8-7X代入④
得关于X的一元一次54X=54达到化归目的。
例3:某工件的形状如图所示,圆弧BC的度数为60˚,B=6cm,点B到点C的距离等于AB,∠ BAC=30˚,则工件的面积等于()
(A)4π (B)5π (C)8π (D)10π
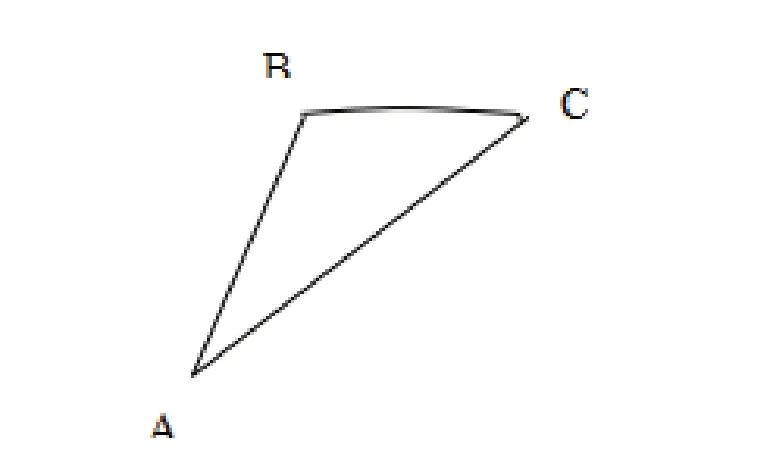
分析:本题所给的图形是陌生的,为此我引导学生设法分解图形,将它转化为我们熟悉的基本图形,如连接,即出现一个等腰三角形ABC和一个弓形,对于弓形可进一步补全图形画出BC所在的圆,将其转化为个圆的面积的问题,显然,其工件面积为6π,选B.

