基于ISSMFA与LMPNN算法的高光谱遥感影像分类

谢福鼎，盖虹羽，杨 俊

(辽宁师范大学 城市与环境学院，辽宁 大连 116029) E-mail：351521039@qq.com

1 引 言

高光谱遥感的最主要特点是图谱合一，其获取的地面空间图像能够融合地物的图像维和光谱维信息，得到每个地物的连续光谱信息，因此研究人员可根据获取的信息进行地物识别和分类.由于高光谱遥感数据的光谱维数高，相邻波段间的相关性强，传统的分类方法容易造成维数灾难，导致分类精度不高.同时光谱分辨率高，导致很多异物同谱的地物在高维空间中可能距离很近，呈云团状成簇分布，这些云团之间并不是呈线性分布的，这种非线性的结构被称为"流形".因此，如何有效地提取出高光谱遥感数据中的地物特征，并且挖掘出其中蕴含的流形，是实现地物准确分类的关键.[1，2]

在处理高维数据的研究中，国内外学者提出了一系列算法，传统的线性降维方法有主成分分析(Principal component analysis，PCA)，线性判别分析(Linear discriminant analysis，LDA)，多维尺度变换(Multidimensional scaling，MDS)[3-5]等.其核心思想是找到一种线性特征变换将高维特征空间变换至低维特征空间，并同时保持样本的某些特性不变.非线性流形算法有等距映射(Isometric feature mapping，Isomap)，拉普拉斯特征映射(Laplacian eigenmaps，LE)，局部线性嵌入(Locally-linear embedding，LLE)，局部保持投影(Locality preserving projection，LPP)[6-9]等.文献[10]提出了边际Fisher分析(Marginal Fisher Analysis，MFA)，有效利用了数据的类别信息，基于图嵌入框架，通过两个图来描述类内的紧密型和类间的分离性，获得线性映射函数，将数据从高维空间投影到低维空间.但由于对遥感影像全部标记较为困难，文献[11]使用半监督算法对MFA进行改进，但并未考虑空间相邻像元间的关系.从物理意义上讲，地理空间上很近的像元在很大概率上属于同类地物，即图像域的空间一致性特点[12].因此，研究人员开始将高光谱影像的空间信息融入到特征提取中，采用空-谱联合的方式，选取合适的地物特征对数据进行维约简.比如文献[13]将光谱角引入空谱联合稀疏表示图像分类理论中，设计空谱联合稀疏表示进行图像分割，有效提高复杂影像的分类精度.

在众多分类方法中，KNN 分类法因具有简单有效，分类准确度高，鲁棒性好等优点，被广泛用于模式识别领域.基于该方法，提出了加权投票方法的KNN[14，15]，给越近的邻居分配更大的权重.但是根据近邻点的距离越近，分配权重越大不是绝对正确的，有时一些更远的邻居的类别信息更为重要.关于这个问题，提出了自适应指标最近邻分类[16].为克服离群点的负面影响，提出了一个简单的非参数分类器，局部平均k近邻[17]，用每类k近邻的局部平均向量来分类待测样本.伪近邻(pseudo nearest neighbor，PNN)[18]则是在距离权重k近邻法(WKNN)[14]和局部平均k近邻基础上提出来的，搜寻每类的伪邻居点，根据最近的伪邻居点的类别来分类.局部平均伪近邻算法[19]则是对PNN算法的推广，用每类的k近邻求得k个局部平均向量，来代替伪邻居点，计算权重距离和，待测点的类别由最近的局部平均伪近邻的类别决定.相比PNN能代表更有效的类别信息，从而提高分类性能.

基于以上分析，本文提出了一种结合空间近邻关系的流形降维(ISSMFA)和局部平均伪近邻(LMPNN)的高光谱遥感影像分类方法.首先在描述类间关系的本征图构建中，融入地理空间近邻像元的信息，设置权重，使得同类或地理空间近邻的像元点更加聚集，从而提取高光谱数据中有效的特征信息进行维数约简，再对降维后的数据用LMPNN方法进行分类.Indian Pine 数据集和PaviaU数据集上的实验结果表明，本文提出的方法能够针对高光谱数据的空-谱特点，有效解决地物点的多分类问题，并且取得较好的分类结果.

2 算法介绍

2.1 半监督边际Fisher分析(SSMFA)

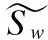
(1)

(2)

(3)

(4)

(5)

目标函数可转化为如下形式：

(6)

于是，上述最优化问题可转化为方程的特征值求解：

XLPXTA=λXLXTA

(7)

解得上式的d个最大特征值λ={λ0，λ1，…，λd-1}，所对应的特征向量{a0，a1，…，ad-1}即为所求的映射A={a0，a1，…，ad-1}.

(8)

(9)

其中β为大于1 的常数

2.2 结合空间近邻信息的半监督边际Fisher分析(ISSMFA)

SSMFA考虑了只有少数样本有标签的情况，进行了改进，但直接运用SSMFA对高光谱数据降维，仅能利用其光谱信息.实际上高光谱影像区别于其他高维数据，具有空-谱一致性的特点，在地理二维空间上距离很近的像元极有可能属于同类地物，仅仅利用现有流形算法中固定的流形结构不能全面的表达高光谱数据的特征信息，导致选取的特征有误，影响后续的分类效果.本文提出的方法，将地理空间近邻像元点加入到SSMFA本征图的构建，赋以更大的权重，从而增强地理空间邻域像元的紧密性，同时保持原高维空间中数据的类内结构和类间结构.

给定一个像元P0，该像元在图像中的位置用(i，j)表示，P0的相邻像元的集合用NP0表示，设邻域窗口大小为m×m(m为大于1的奇数).当m=3时，中心像元点P0的邻近像元为4个或8个，如图1(a)图1(b)所示.同理可推m=5时，它邻近像元为12个，20个或24个…随着窗口增大，中心像元点的近邻像元数增多，可利用的类别信息增多，但同时导致计算量过大，因此本算法只取3×3窗口，8个近邻像元点，通过滑动3×3窗口，不断把近邻关系加入到本征图中.

图1 邻域窗口示意图Fig.1 Schematic of the neighborhood window

假设高维空间RD中一组含n个样本的数据集为X={x1，x2，…，xn}，对于点xi与点xj，如果属于同类，或者互为地理空间邻近像元点，或者互为K近邻，则连起来构成本征图G；如果属于不同的类，则连起来构成惩罚图Gp，以保持样本点类间关系.通过公式(10)(9)获得本征图和惩罚图的权重矩阵，再利用公式(6)(7)求得映射函数及低维构造点.

(10)

2.3 局部平局伪近邻(LMPNN)

(11)

(12)

注意：第一个近邻点的局部平均向量就是它本身.

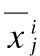
(13)

(14)

4)计算目标函数：

(15)

将距离x最近的基于局部平均的伪近邻的类标签赋给x.(注意：当k=1时，LMPNN等同于NN，PNN，LMKNN).

2.4 算法步骤

本文算法步骤如下：

输入：高光谱数据集和类标签

输出：低维构造点

Step1. 从数据集中每类数据中随机选取一定数量的测试样本

Step2. 构建本征图和惩罚图.对每一个数据点，计算k1近邻，将其连接起来，同时将其空间邻域m×m内的点也连起来，构成本征图.同样每一个数据，计算k2近邻，将不同类的点连接起来，构成惩罚图.

Step3. 根据公式(10)(9)，构造权重矩阵

Step4. 根据公式(6)(7)，计算映射函数.

Step5. 利用映射函数将高光谱数据从高维空间映射到低维空间，得到低维构造点Y.

Step6. 利用LMPNN算法对降维后的点进行分类.

3 实验结果与分析

本文选择Indian Pines数据集和PaviaU数据集进行实验.为验证ISSMFA算法的优越性，同LDA，MFA，SSMFA等降维算法进行对比；为验证LMPNN的分类效果，与KNN分类器进行对比.实验中，分别从数据集的每类样本中随机选取一定数量的训练样本，剩余样本作为测试样本.首先用各特征提取算法对训练样本进行学习，获得投影矩阵，提取样本特征，然后采用各分类算法对测试样本的特征数据进行分类.实验以总精度OA和Kappa系数量化分类效果，为了降低随机性，每个实验重复10次并取平均值作为实验结果.

本文中的参数如下：β为当两个样本点属于同类或者空间位置近邻时的权重系数，k为KNN分类器的近邻数，kL为LMPNN方法的近邻数，根据各数据集中数据分布情况进行调整设定.

本文的实验环境为：实验硬件平台为 Intel(R)Core(TM)i5-4210U CPU，主频为2.40 GHz，内存为4.00 GB，编程环境为MATLAB R2014a.

3.1 Indian Pines数据集实验结果及分析

Indian Pines数据集是1992年6月用AVIRIS传感器采集的美国印第安那州农场的遥感影像，空间分辨率为20m，图像大小为145×145.去除几个受大气影响的波段，剩余200个光谱波段，包含16类地物标记( 20<每类中样本点数<2455)，真实地物标记如图2所示.根据数据分布情况，邻域大小定为3×3，β=1.9，k=2，kL=15，为比较不同训练样本下各算法的性能，分别从每类中随机选取10%，20%，30%作为训练样本，表1给出了各算法在不同训练比例下的总体分类精度(OA)和Kappa系数，和训练10%时各算法的运行时间.表2给出了本文方法与SSMFA在训练20%时，每类地物的分类精度.

图2 Indian Pines影像数据真实地物标记Fig.2 True markings of Indian Pines image data

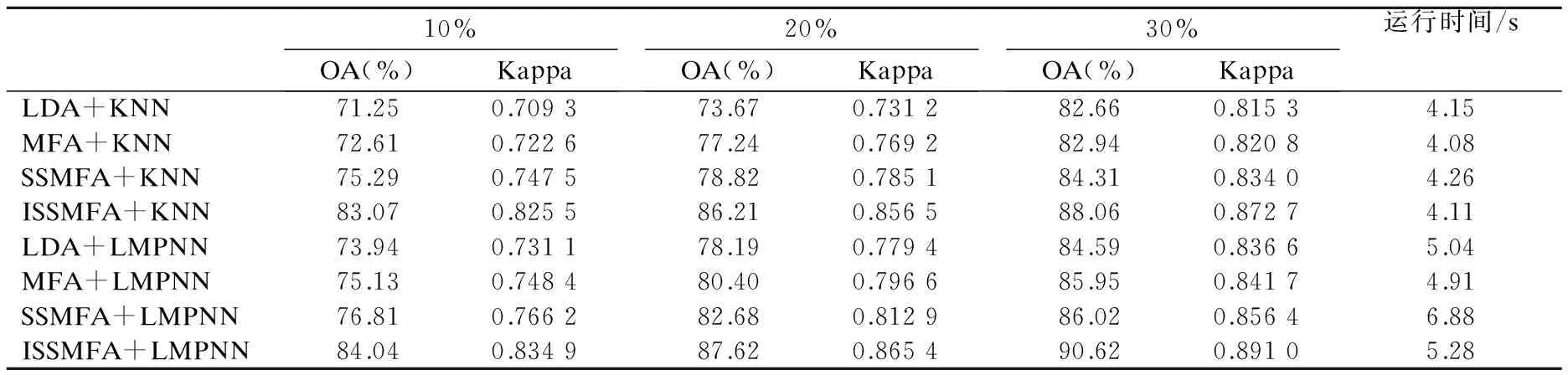
表1 各算法在Indian数据集的分类结果Table 1 Results of the algorithms in the Indian dataset

从表1可知，随训练比例的提高，各算法的精度均有提高，这是因为训练比例提高，可利用的类别信息增多.当分类器为KNN时，MFA比LDA精度高，因为MFA使用了图框架，能挖掘出数据中的流形，保持局部近邻结构不变，加强了同类数据点的紧密性，同时推远不同类数据，使得分类更加准确.ISSMFA比SSMFA高，因为在相同训练比例下，ISSMFA考虑了地理空间邻近像元的位置关系，并把周围8个像元的类别信息用于构图，使得特征提取更加准确.使用LMPNN进行分类的效果普遍比KNN分类器好，是由于，LMPNN考虑了每个类的近邻信息，而不仅仅依据少数近邻点决定其类别，加强了分类的准确性.表2的数据表明，在训练比例为20%时，ISSMFA 总体分类精度能达到87.62%.相比SSMFA方法，ISSMFA对于各类地物均有较好的分类效果，Grass-trees，Grass-pasture-mowed，Wheat，Woods精度均达到0.90以上，其中Grass-trees地物的分类精度提高显著，分类精度达到0.99.

表2 Indian数据集中各地物用不同算法分类后的结果Table 2 Results of the classification of different materials in the Indian dataset

3.2 PaviaU数据集实验结果及分析

PaviaU数据集是ROSIS传感器在意大利南部拍摄的Pavia University，空间分辨率为1.3m，图像大小为610×340，

图3 PaviaU影像数据真实地物标记Fig.3 True markings of PaviaU image data

去除噪声波段，剩余103个光谱波段，此地区共包含9种地物标记(947<每类中样本点数<18649)，真实地物标记如图3所示.设定β=1.3，k=2，kL=13，为比较不同训练样本下各算法的性能，分别从每类中随机选取10%，20%，30%作为训练样本，表3给出了各算法在不同训练比例下的总体分类精度(OA)和Kappa系数，和训练10%时各算法的运行时间.表4给出了本文方法与SSMFA在训练20%时，每类地物的分类精度.

表3 各算法在PaviaU数据集的分类结果Table 3 Results of the algorithms in the PaviaU dataset

从表3可看出PaviaU数据集的总体分类精度比Indian数据集的总体分类精度高，这是由于这两个数据集的数据分布不同导致的，PaviaU数据集中，同类别数据点聚集度较高，不同类别数据点距离较远，因此可分度高，分类精度高.随训练比例增加，各算法精度均有提高，在训练10%，20%，30%时，ISSMFA分别比SSMFA精度高了3.79%，3.34%，3.35%，说明将地理空间邻近像元信息加入到流形构图中能取得更好的分类效果.表4中数据表明，在训练比例为20%时，分别使用SSMFA和ISSMFA相比，Bitumen地物的分类精度提高显著，提高了10%，ISSMFA+LMPNN对每类地物的分类精度均在85%以上，其中Painted metal sheets与Shadows这两类的精度接近100%，总体分类精度达到95.03%.

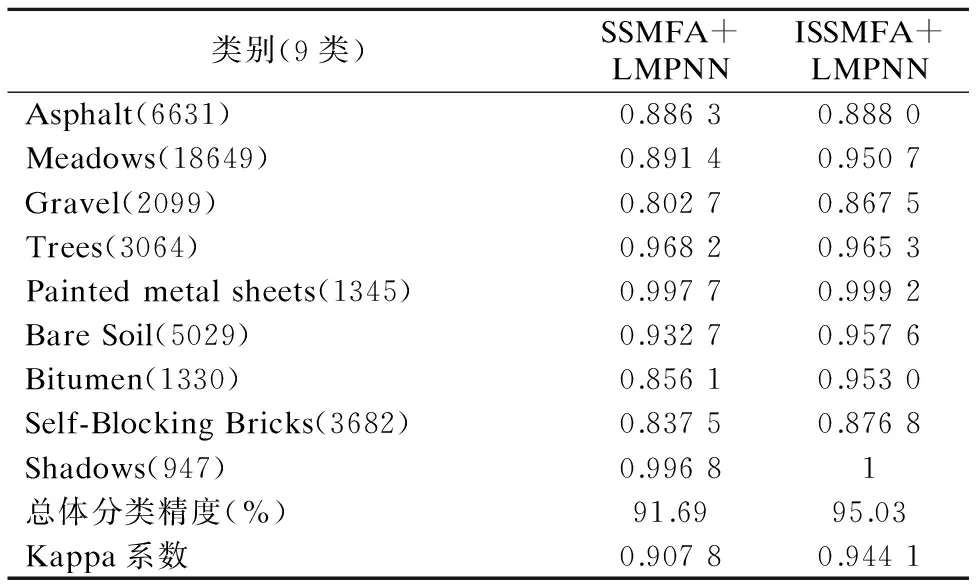
表4 PaviaU数据集中各地物用不同算法分类后的结果Table 4 Results of the classification of different materials in the PaviaU dataset

4 结 论

高光谱影像在地理空间上距离很近的像元点极有可能属于同类地物，仅仅利用现有流形算法中固定的流形结构不能全面的表达高光谱影像数据的特征信息.因此，本文提出了一种结合地理空间近邻关系的流形降维(ISSMFA)和局部平均伪近邻(LMPNN)的高光谱遥感影像分类方法.为证明本文方法的有效性，同LDA，MFA，SSMFA这些降维方法进行对比实验，降维后分别使用KNN和LMPNN两种方法分类.从Indian Pine和PaviaU数据集上的实验可以看出，在各算法降维后，使用LMPNN进行分类要比KNN的分类效果好；在使用相同的分类方法时，相比LDA，MFA，SSMFA这些降维方法，本文提出的ISSMFA方法分类精度明显提高，在训练20%时，总体精度分别能达到87.62%，95.03%.

[1] Xie Yao.Study on hyperspectral image classification based on spatially fitting sparse representation[D].Shenzhen：Shenzhen University，2015.

[2] Wei Feng，He Ming-yi，Shen Zhi-ming，et al.Multi-spectral data based on manifold semi-supervised feature selection[J].Acta Photonica Sinica，2014，43(6)：93-97.

[3] Turk M.Pentland- "eigenfaces for recognition[J].Journal of Cognitive Neuroscience，1991，3(1)：71-86.

[4] Belhumeur P，Hespanha J，Kriegman D.Face recognition：eigenfaces vs.fish-erfaces：recognition using class specific projection[J].IEEE Trans Pattern Analysis & Machine Intelligence，1997，19(7)：711-720.

[5] Trevor C，Michael C.Multidimensional scaling[M].London：Chapman&Hall，1994.

[6] Tenenbaum J，Silva D D，Langford J.A global geometric framework for nonlinear dimensionality reduction[J] .Science，2000，290(5500)：2319-2323.

[7] Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation，2003，15(6)：1373-1396.

[8] Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290(5500)：2323-2326.

[9] He X，Niyogi P.Locality preserving projections[C].In Thrun S，Saul L，et al.Advances in Neural Information Processing System,Cambridge，MA：MIT Press，2004.

[10] Yan Shui-cheng，Xu Dong,Zhang Ben-yu，et al.Graph embedding and extensions：a general frma ework for dimensionality rdeuction[J].IEEE Trans．on Pattern Analysis and Machine Intelligence，2007，29(1)：40-51.

[11] Wang Li-zhi，Huang Hong，Feng Hai-liang.Remote sensing image classification based on SSMFA and kNNS algorithm [J] .Acta Electronic Journal，2012，40(4)：780-787.

[12] Pu Han-ye，Wang Bin，Zhang Li-ming.Dimensional image based on a new algorithm for hyperspectral drop manifold learning[J].Infrared and Laser Engineering，2014，43(1)：232-237.

[13] Wang Cai-ling，Wang Hong-wei，Hu Bing-liang，et al.Study on hyperspectral image classification based on neighborhood segmentation[J].Spectroscopy and Spectral Analysis，2016，36(9)：2919-2924.

[14] Dudani S A.The distance-weighted k-nearest neighbor rule[J].IEEE Trans.Syst.Man Cybern，1976，6(4)：325-327.

[15] Gou J，Du L，Zhang Y，et al.A new distance-weighted k-nearest neighbor classifier[J].Journal of Information &Computational Science,2012，9(6)：1429-1436.

[16] Domeniconi C，Peng J,Gunopulos D.Locally adaptive metric nearest-neighbor classification[J].Pattern Analysis & Machine Intelligence IEEE Transactions on,2002，24(9)：1281-1285.

[17] Mitani Y，Hamamoto Y.A local mean-based nonparametric classifier[J].Pattern Recognition Letters,2006,27(10)：1151-1159.

[18] Zeng Y，Yang Y，Zhao L.Pseudo nearest neighbor rule for pattern classification[J].Expert Systems with Applications，2008，36(2)：3587-3595.

[19] Gou J，Zhan Y，Rao Y，et al.Improved pseudo nearest neighbor classification[J].Knowledge-Based Systems，2014，70(C)：361-375.

附中文参考文献：

[1] 谢 瑶.基于空谱融合稀疏表示的高光谱图像分类技术研究[D].深圳：深圳大学，2015.

[2] 魏 峰，何明一，申志明，等.高光谱数据基于流形的半监督特征选择[J].光子学报，2014，43(6)：93-97.

[11] 王立志，黄 鸿，冯海亮.基于SSMFA与kNNS算法的高光谱遥感影像分类[J].电子学报，2012，40(4)：780-787.

[12] 普晗晔，王 斌，张立明.基于流形学习的新高光谱图像降维算法[J].红外与激光工程，2014，43(1)：232-237.

[13] 王彩玲，王洪伟，胡炳梁，等.基于邻域分割的空谱联合稀疏表示高光谱图像分类技术研究[J].光谱学与光谱分析，2016，36(9)：2919-2924.