基于转换矩阵区分物品时效性的个性化推荐

王 颖,赵海燕,陈庆奎,曹 健

1(上海理工大学 光电信息与计算机工程学院,上海现代光学系统重点实验室,上海 200093) 2(上海交通大学 计算机科学与技术系,上海 200030) E-mail:18502122092@163.com

1 引 言

推荐系统无论在学术界还是工业界都是一直被讨论的研究热点.推荐系统能够使用户从海量信息中找寻到有价值的信息及让有价值的信息提供给对其感兴趣的用户.目前,协同过滤是一种非常流行的推荐算法,又分为基于内存的推荐和基于模型的推荐.基于模型的推荐系统在工业界取得了很好的成效,通过对用户物品的评分或者购买关系建立矩阵并学习隐含特征,以实现推荐.但是,基本的基于模型的推荐系统中并没有将时间因素考虑进去.现实中,用户、物品都会随着时间的推移其特征有不同的变化.一方面,用户会随着时间的变化有不同的兴趣趋向,另一方面,物品的流行度等也会随时间变化.为了得到更好的推荐效果,应该考虑时间因素.在基本的算法基础上,研究者们已经提出了一些模型以考虑用户兴趣或者物品流行度随时间的变化[1-4].

在考虑时间影响中,有一类特殊的时间因素,即对那些上市时间不同的产品(如电影、音乐、衣服)等,人们在选择时将具有不同的理由.例如,对于新的电影,人们会出于大众的评价、当前的热门程度等进行“跟风”式的消费;而对于旧的电影,人们的选择将会更加理性,通常会出于自己对题材、导演或者演员等真正的喜好而观看.这就说明,新旧物品(本文中将上市时间长的物品称为旧物品,刚上市的物品称为新物品,并对用户对旧物品的评分或者使用数据成为旧时间域,用户对新物品的评分或者使用数据称为新时间域)的隐特征、用户对新旧物品上的隐特征具有差异性.目前,对此进行研究的工作尚不多.我们在前期运用了联合矩阵分解对此问题进行了研究并取得了一定效果.但是,联合矩阵分解方法在分解时假设矩阵中具有公共的特征向量,从而导致获得的特征主要决定于数据量大的矩阵,因而具有片面性,无法体现新旧物品特征差异和用户在新旧物品上的选择偏好.

本文中进一步提出了基于转换矩阵的区分物品时效性的推荐算法.通过对转换矩阵的学习,一方面充分考虑了新旧物品隐特征、用户对新旧物品上的隐特征的差异性,另一方面又考虑了它们的相关性,能够较好地适应数据稀疏和冷启动的问题.

本文后续内容组织安排如下:第2节介绍了相关工作,重述了有关时间因素上的推荐研究和单域及多域上的基于模型推荐的算法;第3节量化的分析了各个域中物品隐特征、用户对物品隐特征的差异性;第4节是基于转换矩阵的区分物品时效性算法的详细介绍;相关实验及实验结果在第5节中进行了叙述.第6节是算法的总结及未来工作方向的分析.

2 相关工作

2.1 考虑时间因素的推荐

“时间”在推荐系统中是一个不可忽视的因素,研究者已经提出了一些模型来考虑时间对物品和用户的影响.在[1]中,Ding认为在推荐过程中,算法应该加大用户近期时间的兴趣对推荐结果的影响,而用户之前感兴趣的物品的贡献值要小于他现在感兴趣的物品,因而在协同过滤的基础上通过引入时间衰减函数来提高推荐系统的准确度.文献[2]中,作者通过用户行为的先后顺序,利用决策树算法对其进行建模.这也是考虑了用户随着时间的推移,对物品的兴趣发生了变化.在文献[3]中作者提出BPTF算法,利用矩阵分解模型,把时间作为新的一维,再采用张量分解的算法对数据进行建模,然后用贝叶斯来避免调整参数和控制模型的复杂性.在文献[4]中,作者提出了TimeSVD算法,在常规的加偏置项的SVD模型的基础上增加时间特征向量,使用户的特征向量、物品的特征向量可以隐式地从时间数据信息中学习,获取更多的信息提高推荐系统的精度.在文献[5]中该算法通过用户-项目二分图为基础,引入衰减函数,将时间综合信息对推荐的影响量化成图节点的关联概率;然后采用轮盘赌模型根据关联概率选择游走目标;最终对每个用户做出top-N推荐.以上研究虽然将时间考虑到推荐算法中,也一定程度上提高了推荐系统的精度,但是这些研究只是简单地将时间融合在基本模型上,没有考虑新旧物品隐含特征的联系及区别,以及用户选择新旧物品时出发点的不同.

在推荐算法中,基于模型的推荐算法取得了很好的成效,接下来我们介绍单矩阵分解和多域矩阵分解.

2.2 基于模型推荐

2.2.1 矩阵分解

矩阵分解(MF)[5]是基于模型的推荐算法的代表,它将一个评分矩阵分解成两个低秩的矩阵:即用户特征矩阵和物品特征矩阵.通过用户特征和隐类之间的关系,物品特征和隐类之间的关系,预测用户对物品的喜好程度.矩阵分解解决了单一领域上的推荐问题.但是现实中用户物品不仅仅是涉及一个关系域中的信息,而是可能涉及很多的域并相互影响.所以为了提高推荐精度,应该考虑将多个关系域中的数据在矩阵分解时利用起来.

2.2.2 多域矩阵分解

学者们近年来提出了联合矩阵分解(Collective Matrix Factorization,CMF)[6]方法,它将多个有联系的矩阵同时进行分解,这些多个矩阵通过共享的一维向量进行联系.该算法是将用户看作是一个立体的多维用户,挖掘不同域上矩阵分解所得特征向量之间的联系.联合矩阵分解对某些领域上的冷启动问题可以提供解决方案.但是该算法也有一些缺点:CMF学习训练得出的共享特征向量受这些域中数据量大小的直接影响,即共享特征向量主要是从数据量大的域中学习出来的,而忽略了数据量小的域中特征向量;其次,如果多个域中有冷启动的域,则统一特征向量主要是学习没有冷启动的域中的数据.这些特点使得该模型应用与本文研究的问题时也有一定的不足:根据不同时间节点划分的新旧时间域上的数据量、冷启动情况具有差别,这样共享的用户特征向量主要从数据量多的域中或没有冷启动的域中学习出来,而忽略了其他不满足条件的域中的信息数据,从而使得共享特征——用户特征不是很准确,无法更好地对不同时间域上用户对物品隐特征的差异性进行学习.

在[7]中提出了称之为异构矩阵分解的算法.它认为物品的特征在不同场景下需要通过对基本特征进行转换,为此,通过最大似然来对特征和转换矩阵进行学习,并通过EM算法对模型参数进行求解.该算法的复杂度很高.另外,由于最大似然定义在对所有评分上,依然存在学习出的模型偏重于数据多的领域的问题.本文在目标函数中对普通域、时间域上的偏差进行单独建模并通过参数调节其重要性,能够适应数据不平衡问题.基于本文设计的目标函数,我们设计了相应的随机梯度下降算法.

3 模型数据分析

通过第2节对相关工作的分析,可以知道目前已经有一些推荐中考虑时效性的研究工作.但是,本文中考虑的时效性具有特殊性,即我们的目标是区分新旧物品隐特征、用户对新旧物品上的隐特征的差异性.那么这一现象是否是事实呢,我们可以对数据进行分析来揭示这一现象.GroupLens小组提供的MovieLens数据集是一组从20世纪90年末到21世纪初由MovieLens用户提供的电影评分数据,该数据集有2113的用户,有10109部电影.我们的分析和实验都在该数据集上进行.

我们先来定量地分析用户的基本特征向量和用户在新、旧时间域上用户特征向量的不同.在本算法中用欧式距离来衡量不同时间域物品的隐特征及用户对物品的隐特征的差异.两个n维向量a(x11,x12,…,x1n)与b(x21,x22,….x2n)的欧式距离:

(1)

如公式(1)中,d是两个n维向量的距离.距离值d越小,说明两个不同域中的同一特征向量的差异小.我们通过对不同矩阵的分解可以得到用户的特征向量,然后衡量同一用户的特征向量的差别.

图1中横坐标是特征向量的距离,纵坐标是落在这个距离区间上的用户数量.从图1上可以看到统一特征向量和旧时间域上的用户特征向量集中落在距离为1.5到3之间,在距离为2.5上的用户达到最高—1200.而统一特征向量和时间域上的用户特征向量在2.5-3.5范围之间,用户量最大的是落在这两个区域为3的距离上.从图1中可以看出用户对新旧物品隐特征存在差异,所以不能将用户的隐特征看作是同一特征向量,而是应该区别对待不同的域中的隐特征.接着又计算了用户对新旧物品的隐特征之间的距离.这两个域上的距离在3.5和4的用户为600.所以新时间域和旧时间域上的用户对物品的隐特征还是有很大区别的.

图1 用户特征向量之间距离分布图Fig.1 Distribution of the distance between the user factors

下面考虑物品之间隐特征的区别,如图2所示.

图2中的横坐标是不同域上的特征向量的距离,纵坐标上是落入相应距离的用户数量.物品在不同时间域上也是有差异的.而且不同时间域上的物品和基本域上物品的特征向量也是有很大区别的.

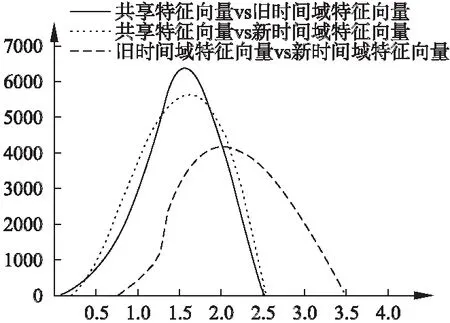
图2 物品特征向量之间距离分布图Fig.2 Distribution of the distance between the item factors

通过上面的数据分析,可以明确看出不同域上的同一物品特征向量确实有自己的特性.这与我们的经验是一致的.用户具有基本的喜好趋向,例如,用户喜欢的电影题材(动作、爱情、喜剧、灾难等)等.对于新电影,用户会根据这个时期的潮流、电影中的新技术、或者是电影的口碑效益等来选择观看的影片,而对于以前的老电影的选择很大程度是源于用户对它的某种情感,带着怀念的情感来欣赏的.

4 异构矩阵分解的时效性推荐算法

4.1 算法思想介绍

基于之前的数据分析,我们知道了用户对物品的隐特征或物品的隐特征在不同时间域上是不同的,而且与用户或物品的基本域上的用户特征也有很大的区别.所以仅仅基于CMF模型来学习用户的共享特征矩阵对推荐的精度是不准确的.需要将用户或物品的基本隐特征的信息迁移到用户或物品的在新旧时间域上来.这时就要通过学习转换矩阵,将基本域上的隐特征转换到特定时间域上来,挖掘用户或物品更多的信息,考虑这些域上的差异性与相关性,提高推荐的精度.

我们设计出基于转换矩阵区分物品时效性的个性化推荐算法.本算法的核心在于考虑新旧时间域上的物品或用户与基本域上的物品和用户差异与联系;还有用户对新旧域上物品的选择的消费动机存在差异性.

本模型由三个矩阵构成,分别为Base Matrix,Old Matrix,New Matrix.Rbase(例如用户观看的全部影片的评分)中填充的是用户对所有物品的评分,这个矩阵代表用户对物品基本的喜好特征;Rold(例如观看的旧电影的评分)中是对旧物品的评分记录,这里的旧时间域是在T时间分界点之前的所有物品的评分;Rnew(例如观看的新影片的评分)是距离T时间分界点之后出现的物品的评分.在本算法中,T是一个变量,可以调节T这一参数来划分不同的新旧时间域,从而导致新时间域和旧时间域上用户观看的影片数量的不同.

p、q分别代表用户和物品各自在Rbase的基本特征向量,pold和qold分别代表用户和物品在Rold的特征向量,pnew和qnew分别代表用户和物品在Rnew的特征向量.将用户或物品的基本特征向量迁移学习到新时间域上的用户或物品的特征向量的转换矩阵分别为Mpnew、Mqnew;将用户和物品的基本特征向量迁移学习到旧时间域上的用户或物品的特征向量装换矩阵分别为Mpold、Mqold.既可以找到不同域上特征向量与基本域特征向量的差异,又能将其紧密联系,较好地适应数据稀疏和冷启动的问题.

4.2 算法公式推导

目标函数涉及三个域的矩阵分解,并且还有从基本域迁移学习到新时间域的转化矩阵.首先构造目标函数如下:

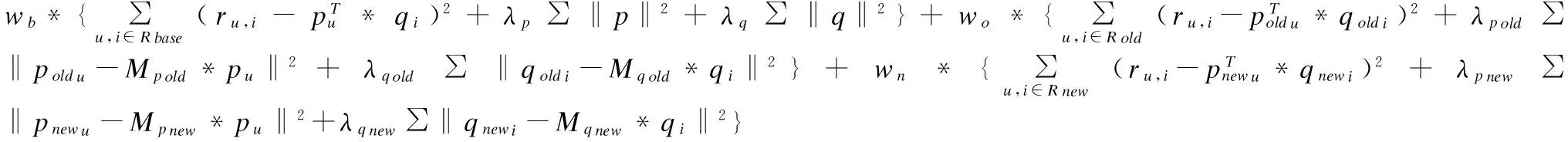
(2)

公式(2)是我们需要构建的目标函数.其中u代表的是用户,i代表的是物品(电影).ru,i表示的是用户u对物品i的真实评分.wb、wo、wn分别是基本域、旧时间域、新时间域上矩阵的权重.λq、λp、λpold、λqold、λqnew、λpnew分别代表对应矩阵的正则项系数.该目标函数也是我们预测出的值相对于测试集中一致数值的偏差.同传统的MF算法一样使用梯度下降的训练方法来进行最小化目标函数,各个矩阵求其偏导如下:

对基本域上的用户和物品求偏导,如公式(3)、(4).

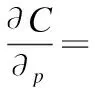
wo*{2λpold(poldu-Mpold*pu)(-Mpold)}+wn*{2λpnew(pnewu-Mpnew*pu)(-Mpnew)}

(3)

wo*{2λqold(qoldi-Mqold*qi)(-Mqold)}+wn*{2λqnew(qnewi-Mqnew*qi)(-Mqnew)}

(4)

如公式(5)、(6)对旧时间域上的用户和物品转换矩阵求偏导.公式(7)、(8)是对新时间域上的用户和物品转化矩阵求偏导.

(5)

(6)

(7)

(8)

如公式(9)、(10)对旧时间域上的用户和物品矩阵求偏导.新时间域上的用户和物品求偏导如公式(11)、(12).

(9)

(10)

qnewi)(-qnewi)+2λpnew(pnewu-Mpnew*pu)}

(11)

(12)

上面的公式是每次迭代需要更改的变量.这些变量包括基本域上用户及物品特征向量,还有新、旧时间域上的用户及物品特征向量以及转换矩阵.

然后变量包括基本域上用户及物品特征向量,还有新、旧时间域上的用户及物品特征向量以及转换矩阵每一次迭代按如下的公式(13)-(22)更新.

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

通过多次迭代更新会得到我们需要的不同域上的特征向量和转换矩阵,在测试集上进行新时间域上的推荐或是旧时间域上推荐.

4.3 算法描述

4.3.1 数据预处理和参数初始化

本算法实现的第一步是将数据集进行相应的处理和参数的初始化.首先将数据集填充到Rbase中,在将数据集根据自己预定的T来进行划分新旧时间域:时间小于T上的产品数据填充到Rnew上,时间大于T上的产品数据填充到Rold.然后在给不同域上的用户及物品特征向量初始化,并且使得基本域到新旧域上的转换矩阵初始化为单位矩阵.

4.3.2 算法描述

在本算法中涉及到的一系列参数进行了初始化,接下来就是需要对这些参数进行训练并使该目标函数达到收敛.分为以下几个步骤:

1)使用遗传算法得到权重参数wb、wo、wn(该算法中用weight是一个包含基本域、旧时间域、新时间域的权重参数的数组);

2)把遗传算法得到的权重参数代入本算法中;

a)使用梯度下降算法训练直到目标函数C的值收敛至最小值;

b)在最后目标函数C值收敛时,计算测试集的评分与预测评分的平均绝对误差(RMSE).

伪代码如下:

Input:sourcefile,n,alpha,lambd,F,T

Output:p,q,pold,pnew,qold,qnew,Mp_new,Mq_new,Mp_old,Mq_old,RMSE

Function:

THMF

//Initialize the Parameters for different time domains

Begin

Initialize{p,q,pold,pnew,qold,qnew,Mp_new,Mq_new,Mp_old,Mq_old}

{Rbase,Rold,Rnew} from sourcefile according to time

// Gradient descent method

do

n←the maximal number of iterations;

t←1;

whilet≤n:

Compute the objective functionf

by Equation (2);

Update{p,q,pold,pnew,qold,qnew,Mp_new,Mq_new,Mp_old,Mq_old} by gradient descent algorithm;(13-22)

if convergence then

break;

Endif

t←t+1;

Endwhile

End

Return{p,q,pold,pnew,qold,qnew,Mp_new,Mq_new,Mp_old,Mq_old}

//calculate the rmse

return RMSE

// Genetic Algorithm

Input:pm,pc,M,G,Tf,Pop

Output:fit

Function:

GA

Begin initialize {pm,pc,M,G,Tf,Pop}

do

Fit:=THMF

Initialize newPop

do

Choose,crossover,mutate individuals

until numbers of elements in newPop grows to beM

Pop=newPop

until fit<=Tf or numbers of generation grows to be G

End

return fit

在上述THMF算法描述中,Input参数中的n是迭代的最大次数,alpha是步长,也就是每次按照梯度减少的方向变化多少.Lambd是包含多个域中的正则向系数.F是特征向量中隐类的的个数,T是划分物品新旧的分界点时间.下文中对这些参数进行了实验与分析,找到适合本算法的参数.本文算法评价指标是通过均方根误差(RMSE)来计算.RMSE可以衡量算法的准确度,通过将训练出来的特征向量来预测测试数据集中的评分,进而和测试集中的实际评分比较,预测的评分越接近,说明算法的精确度越高.

5 相关实验

本节主要是对上述的模型算法在相关的数据集上进行验证,并按照RMSE评价指标进行相关的算法效果的比较.

5.1 数据准备

本算法考虑了用户和物品在新旧域上特征向量的区别,所以需要选择的数据集应该具有时效性.我们熟知的电影是具有时效性的产品,可以满足本算法的多时间域划分.

该数据集中每个条目由用户ID、电影ID、评分和时间戳这四元数据组成.在实验的时候按照1:8的比例划分测试集、训练集.将训练集中的全部数据作为基本域,将训练集的评分数据通过时间戳将电影划分为新时间域和旧时间域.用该数据集来验证本文提出思想:通过用户对物品的隐特征,物品隐特征的差异和相关来更好的探究用户对不同时间物品选择偏好的动机.

5.2 实验内容

实验中实现了以下的算法:

传统的MF模型(MF):用单域矩阵分解预测用户对电影的评分.该模型没有考虑时间因素的影响,只是简单的学习用户对电影的历史评分,来挖掘用户对电影的喜好.

基于CMF模型产品时效性感知的推荐算法(TCMF):该模型是按照T来划分新旧时间域,将用户特征向量作为这两个矩阵共享一维,联合训练数据.得到共享用户特征矩阵和新旧时间域上的物品特征向量.

基于转换矩阵考虑的物品时效性个性化推荐模型(THMF):该模型有三个域:基本域、新时间域、旧时间域.在实现时,通过遗传算法进行了参数调优.

该模型通过对转换矩阵的学习,一方面充分考虑了新旧物品隐特征、用户对新旧物品上的隐特征的差异性,另一方面又考虑了它们的相关性,能够较好地适应数据稀疏和冷启动的问题.可以有效的探究用户在不同时间下对物品选择偏好的不同的动机趋向:受社会潮流还是受自身兴趣喜好的因素.

5.3 实验结果

如图3是MovieLens上的数据集在MF、TCMF、THMF模型上得到的实验结果.

表1 不同迭代次数下不同算法的rmse的变化
Table 1 Variation of RMSE with different algorithms in different iteration

Algorithm/iterations10204060MF0.85030.81910.80660.8059TCMF0.84230.80940.78820.7811THMF0.82710.79300.77330.7703

从图3可以看到随着实验迭代次数的增多,RMSE的值是越来越小的,最后达到收敛值.多域上的矩阵分解确实比单域上的矩阵分解的效果要好.并且THMF算法相比TCMF算法的在任何迭代次数下RMSE的值都是最小的.TCMF在一定程度上解决了数据的冷启动问题,但该模型的统一特征向量的学习还是依赖于数据量稠密和数目多的时间域.所以预测的评分要比THMF预测评分误差大一些.从实验数据中也可以观察到将电影划分为新旧电影,来分开考虑用户对电影的选择偏好的动机比没有将电影划分为新旧电影的预测的评分要准确很多;而且在本次实验中通过转化矩阵来区别和联系基本域上的隐特征和特定域上的隐特征,也进一步提高了预测评分的精度.

图3 不同迭代次数下不同算法的RMSE的变化Fig.3 Variation of RMSE with different algorithms in different iteration

接下来考虑THMF的一些参数对该模型的影响.

1)权重

因为该模型通过遗传算法对不同域进行权重的选择,最后选择出来的权重是wb=0.2、wo=0.5、wn=0.3,我们也人为赋予了不同的权重进行了比较.wb:wo:wn=2:5:3时,预测评分的结果误差是最小的.如图4横坐标是三个域权重之比,纵坐标是RMSE.图4所示基于域的数据权重没有很影响预测评分,这里基本域的贡献通过转换矩阵将基本隐特征转到各个特定的域中去.所以预测评分的误差还是主要取决于时间的影响.而且当旧时间域上的权重比新时间域上的权重大些,则最后的误差比较小.这又充分说明了用户选择旧物品是基于自己本身的喜好,对新物品的购买是基于冲动行为,所以再次推荐新物品给该用户,该用户不再选择.

2)步长

如图5,横坐标是表示步长,纵坐标是RMSE的值.步长也会影响算法的RMSE,通过对该算法进行不同步长的实验,发现找到最适合的步长为0.001到0.0012,其RMSE最小.

图4 不同域的不同权重比的THMF算法RMSE的比较Fig.4 Comparisons of RMSE between different weights of different domain in THMF

图5 THMF在不同步长下的RMSE的比较Fig.5 Comparisons of RMSE with differentstep sizes in THMF

图6 不同时间T下的RMSE的变化Fig.6 RMSE withdifferent T

3)时间T选择

通过时间的划分为不同的时间域上的电影,这决定了不同域上电影的数目.如图6,横标是T时间,单位是月,纵坐标是RMSE.实验表明,在T定为24个月的时候,其预测评分误差是最小的.

6 结 论

本文中经过数据量化分析,得出统一特征向量和划分新旧物品形成的不同域上学习的特征向量具有差异性,因而,对这部分差异进行建模,会使预测评分更准确.文中基于此想法,设计了相应的算法,算法中通过转换矩阵,将不同时间下用户对物品的隐特征及物品隐特征的差异和联系充分考虑进模型,最终得到用户选择具有不同时效性物品的偏好模型.实验表明本算法能够提高推荐效果.从实验中可以看出:

1)当新物品的权重比较大时,最终的评分误差很大,这反映了新物品并不一定反映用户的真正喜好,对新物品的选择受到潮流和从众心理的影响,而相对而言,旧物品的选择是跟随自己内心的喜爱选择的;

2)用户对物品基本域上隐特征通过转换矩阵学习到各个时间域上,将其中的差异区别开,又将其联系起来,可以得到了很好的推荐精度.

本算法虽然取得了一定的效果,但是仍然有许多值得扩展的地方.例如,这里谈论的都是用户物品和隐类的关系,在后面的研究可以考虑将物品用户的显性特征融合起来,并且还可以加上上下文推荐.这都是后续将继续研究的方向.

[1] Ding Y,Li X.Time weight collaborative filtering[C].ACM CIKM International Conference on Information and Knowledge Management,Bremen,Germany,October 31-November,2005:485-492.

[2] Zimdars A,Chickering D M,Meek C.Using temporal data for making recommendations[C].Morgan Kaufmann Publishers Inc,2001.

[3] Xiong L,Chen X,Huang T K,et al.Temporal collaborative filtering with Bayesian probabilistic tensor factorization[C].Siam International Conference on Data Mining,SDM 2010,April 29-May 1,2010,Columbus,Ohio,Usa,2010:211-222.

[4] Christensen I,Schiaffino S.Matrix factorization in social group recommender systems[C].Mexican International Conference on Artificial Intelligence，IEEE Computer Society,2013:10-16.

[5] Zhao Ting,Xiao Ru-liang,Sun Cong,et al.Personalized recommendation algorithm integrating roulette walk and combined time effect[J].Journal of Computer Applications,2014,34(4):1114-1117.

[6] Singh A P,Gordon G J.Relational learning via collective matrix factorization[C].Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,ACM,2008:650-658.

[7] Jamali M,Lakshmanan L.HeteroMF:recommendation in heterogeneous information networks using context dependent factor models[C].International Conference on World Wide Web,ACM,2013:643-654.

[8] Xiang L,Yang Q.Time-dependent models in collaborative filtering Based recommender system[C].Ieee/wic/acm International Conference on Web Intelligence,Wi 2009,Milan,Italy,15-18 September 2009,Main Conference Proceedings.DBLP,2009:450-457.

[9] Sun G F,Wu L,Liu Q,et al.Recommendations based on collaborative filtering byexploitingsequential behaviors[J].Journal of Software,2013,24(11):2721-2733.

[10] Liu J,Wu C,Xiong Y,et al.List-wise probabilistic matrix factorization for recommendation[J].Information Sciences,2014,278(1):434-447.

[11] Daneshmand M S,Javari A,Abtahi E S,et al.A time-aware recommender system based on dependency network of items[J].Computer Journal,2014,58(9):1955-1955.

[12] Xiang E W,Liu N N,Pan S J,et al.Knowledge transfer among heterogeneous information networks[C].ICDM Workshops 2009,IEEE International Conference on Data Mining Workshops,Miami,Florida,Usa,6 December,DBLP,2009:429-434.

附中文参考文献：

[5] 赵 婷,肖如良,孙 聪,等.融合时间综合影响的轮盘赌游走个性化推荐算法[J].计算机应用,2014,34(4):1114-1117.