一种加权复杂网络中社团发现的凝聚算法
张 昕,楚善增,姚友娟,张 瑜,李晓光
(辽宁大学 信息学院,沈阳 110036) E-mail:xgli@lnu.edu.cn
1 引 言
现实世界中的许多系统都是以复杂网络的方式呈现,如电力网络、交通网络、社会网络以及互联网等,它们不仅具有小世界与无标度等结构复杂性,还表现出动态演化、连接多样性以及节点多样性等诸多复杂性质.社团结构[1]是复杂网络众多重要特性之一,而根据网络中所蕴含的信息解析出有价值的社团拓扑结构,即社团发现则是复杂网络研究领域中的一个重要方面,不仅具有重要的理论价值,对于许多现实系统还有广泛的应用前景[2-4].
社团发现算法一直备受众多研究人员的关注,如GN算法[5]、谱分析算法[6]、层次聚类算法[7]以及一些综合多种思想的算法[8,9]等.另外,还有部分工作重点针对重叠社区的发现,如基于团渗理论的CPM算法[10]、基于局部扩展的LFM算法[11]、基于集成网络的UEOC算法[12]以及基于连接划分的边社区发现算法[13]等.但现有研究大多是针对无权网络,而相比于无权网络,现实系统更适合抽象为加权网络.例如交通网络中,道路的运输能力自然可以作为边的权值;在人际关系网络中,则可以将关系的紧密程度作为权值,能够更为直观、准确的反映网络中人与人之间的联系情况.而且,不同于机会网络中的不确定连接[14],大多数现实系统中的节点关系普遍较为稳定.因此,加权网络相关研究显然具有更好的应用价值.
目前针对加权网络的社团结构发现研究较少[15],典型的成果有CNM算法[16]、WGN算法[17]和Newman快速算法(FN算法)[18].CNM算法基于堆的数据结构来计算和更新网络的模块性上提出的一种新的贪心算法,该算法虽然在模块度增量矩阵△Q、最大堆H以及辅助变量a三种数据结构的基础上节省了存储空间,使其时间复杂度接近于线性,但只适用于对准确度要求不是非常严格的复杂系统中.
WGN算法(加权的GN算法)是对GN算法的一种改进.由于该算法是通过不断的计算网络中每条边的介数,找出并删除其中介数最大的边之和,需要再重新计算各边的介数值,以至于该算法的时间复杂度较高,最差情况下为O(m2n),其中m为边数,n为节点数,因此该算法只适用于节点数量相对较少的中小规模的网络中.
Newman快速算法(FN算法)基于贪婪算法的思想,首先将网络中的每个节点看成是一个单独的社团,在计算出的网络中每个节点对的相似性的基础上进行合并,其时间复杂度为O(n2).该算法对于大规模网络下的社团划分具有优良的性能,但精确度略低于GN算法.
现有加权网络社团发现算法基本上是对无权网络社团结构发现算法的一种调整或修改,这种细微的改变对加权网络社团结构的刻画较为浅显,对应的社团发现能力也十分有限.本文在现有研究工作基础上,提出一种改进的加权网络社团结构定义,更为符合现实网络中社团的实际情况,并进一步提出了一种新的加权网络社团发现算法,能够更为准确有效的发现加权网络中的社团结构.
2 加权网络社团结构定义
合理准确的社团结构定义对于网络建模、社团结构评价以及社团发现算法来说,都是必要的前提,更是进一步研究工作的基础.现有的研究工作中,基于相对连接频数的强/弱社团定义是一种比较普遍的形式.本节分析该类定义在无权网络与加权网络上的对比差异,并给出改进的加权网络强/弱社团定义.
2.1 目前加权网络社团结构定义

图1为无权网络中的强弱社团示意图,图中左部空心节点构成的子图为强社团,而在右部实心节点构成的子图中,节点v1与节点v2不满足强社团条件,因此右部子图为弱社团.

图1 无权网络中强/弱社团Fig.1 Strong/weak community in unweighted network


图2 加权网络中强/弱社团Fig.2 Strong/weak community in weighted network
图2为加权网络中的强弱社团示意图,左部空心节点构成的子图与右部实心节点构成的子图均为强社团.该结论和无权网络情况下的社团结构划分存在差别.
考虑社团的本质含义,即社团内节点间连接紧密而社团间的连接稀疏,显然节点的度是决定社团结构及性质的主导因素,而节点间连接的权重是次要因素.由于加权网络中综合考查了连接权重,其社团形成条件较之无权网络更为严格,因此同结构的加权网络与无权网络中社团发现的结果应一致,或无权网络中的强社团由于权重的影响退化为弱社团.因此可以看出,上述加权网络社团划分条件过度强调了权重对社团的影响,弱化了节点度的影响,使得结果与社团本质含义存在偏差.
2.2 改进的加权网络社团结构定义

(1)
综合考虑连接权重以及节点度对社团的影响,给出改进后的加权网络中强/弱社团定义如下:


图2所示加权网络,按上述定义进行社团划分,则图中左部社团为强社团,右部社团为弱社团结构,与无权网络中的划分结果一致.由此可见,本文定义利用节点度和权重同时对社团结构进行约束,较原有加权网络社团发现条件更为合理.
以图3所示Zachary空手道俱乐部网络[19]为例,进一步验证本文定义的合理性.该网络体现了美国某大学的空手道俱乐部会员之间的社交关系,包含34个节点以及78条边,划分为2个社团,是复杂网络社团划分算法准确性衡量的一个代表性数据集.图3中包含两个已知的社团,节点颜色的深浅代表其社团归属,节点间连线上的数字表示权重.
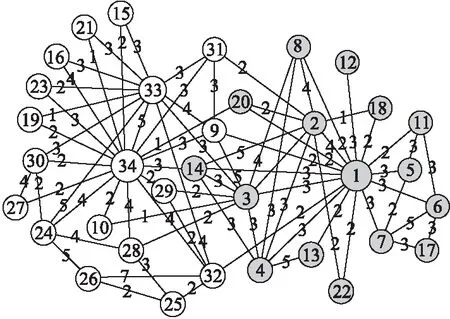
图3 空手道俱乐部网络Fig.3 Zachary network
根据社团所属情况以及连接的权重信息,可以得出各项统计值如表1所示.
表1 空手道俱乐部网络社团统计量
Table 1 Community statistic in Zachary network

统计量∑kin∑kout∑sin∑soutwinwout社团166101992632.6社团26910219223.22.2
首先忽略连接的权重信息,按无权网络对图3进行分析.图中节点3的kin=kout=5,因此社团1不满足强社团条件,但从社团1整体来看,有∑kin=66>∑kout=10,因此社团1为弱社团.图中节点10的kin=kout=1,因此社团2不满足强社团条件,但从社团2整体来看,有∑kin=69>∑kout=10,因此社团2也为弱社团.
然后依据原有加权网络强/弱社团划分条件,按加权网络对图3进行分析.显然,社团1与社团2中每个节点均有sin>sout,因此二者均为强社团,与无权网络分析所得结论矛盾.由此可以看出,原有加权网络强/弱社团划分条件中权重的影响力过大,弱化了节点度作为社团结构的主要影响因素的作用,因此其合理性不足.
3 加权网络中社团发现算法
结合现有社团层次凝聚思想,以本文给出的加权网络社团定义为基础,给出相关度量指标,并进一步提出一种新的社团发现算法(ER-NE算法),能够更为准确的发现加权网络中的强/弱社团结构.
3.1 关联性及有效性指标
层次凝聚思想中,典型的社团归属判定条件具有传递性,即节点1与节点2归属同一社团,且节点2与节点3归属同一社团,则节点1与节点3也归属同一社团.这种传递性并不严谨,特别是对于大多具有社团重叠特征的实际网络来说,多个节点是否属于同一社团需要分别判定.为避免传递性质出现,并充分体现本文社团定义中对连接权重及节点度的综合考虑,给出ER-NE算法中相关指标的定义如下:
定义3.(边社团关联性ER)边社团关联性表示边在其两端点各自邻域内权重比例的均值,节点vi与vj间的关联性大小记作ERij,具体计算方法如式(2)所示:
重视培养学生的能力,一直是我国基础教育改革与发展的重要目标。对于能力的培养,既有一般目标,也有各自学科的特殊要求和特殊问题。教育不能只满足知识的传递,而是应该将重点放在提高学生能力的培养上,才能将“知识”转变为“智慧”,才是素质教育的应有之义。
(2)
式(2)中Ni与Nj分别表示节点vi与节点vj的邻域,wij表示连边权重,若节点vi与vj不相邻,则ERij=0.
边社团关联性描述了两个相连节点之间关联性的大小.根据本文给出的加权网络中的社团定义,社团内部节点间连边的数量与权重之和都要大于社团内部节点与外部节点的连边.由式(2)可以看出,节点间连边的权重越大,节点的度值越小,则相连的两节点之间的关联性就越大,体现了权重与节点度的双重因素.若节点v与社团C内节点的累积关联性越大,则节点v属于社团C的可能性越高,由此定义节点社团有效性如下:
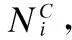
(3)
节点社团有效性表示一个节点加入社团后,该社团仍然成立的可能性.由式(3)可以看出,节点社团有效性取决于该节点对社团内节点的累计关联性占该节点整个邻域内的累积关联性之比,即社团有效性的值越大,则节点与社团内部节点的关联性越高.同时,这种关联性是由式(3)定义的,既符合社团内部连接紧密的基本要求,又满足本文对权重与节点度的双重考虑,能够有效的刻画节点属于符合本文定义社团的可能性.
3.2 算法描述
本节给出在网络中发现符合本文定义社团结构的算法——ER-NE算法.在进行社团划分之前,可能已知部分相关信息,如网络中社团数量、某对节点属于同一社团等.这些信息称作先验信息集,若先验信息集存在,则算法可以根据该信息集确定部分初始动作.算法具体描述如下,若先验信息未知,则其中输入信息k值为0,H为空.
输入:原始加权网络G,已知的社团数量k,已知节点对同属信息H
输出:划分所得社团集合C
1 ifk==0

//flag标记k初始是否为0,其初始值为false
3 计算邻接ER矩阵;
4C=Ø;
5 while |C| 6 选取剩余部分中ER值最大的节点对→C; //剩余部分是指不包含在社团中的部分 7 if 社团之间存在重叠节点 8 合并重叠社团; 9 for 所有社团Ci∈C 10 forCi所有邻接点v 11 ifNE(v,Ci)>0.5 12v→Ci; 13 ifflag 14 for 所有社团Ci∈C 15 if 社团之间存在重叠节点&&合并后符合本文定义 16 合并重叠社团; 17 ifH≠ø 18 forH中所有节点对 19 ifvi(或vj)已存在于某社团 20vj→vi所在社团(或vi→vj所在社团) 21 for 所有剩余节点v 22 forv所有邻接社团Ci 23 计算NE(v,Ci) 24v→Cmax; //Cmax为NE(v,Ci)值最大的社团 25 ifv∈H 26v的关联节点→Cmax; //v的关联节点为H中已知与v属于同一社团的节点 27 if 存在剩余节点 28 goto 步骤21 29 returnC 算法中步骤1-2判断社团数量是否已知,并设置标志位,若社团数量未知,则置初始社团数量为网络中节点数量的平方根.步骤3-4初始化社团集合为空,并根据输入的网络数据计算邻接ER矩阵. 步骤5-8以ER值最大的节点对为基础构建初始社团,若这些节点对直接相连,则将其合并,并依据ER值排序补充新的初始社团. 步骤9-12在现有社团的邻域内选择NE大于0.5的节点,将其划分至对应社团.按式(3)给出的节点社团有效性定义来看,节点的NE值大于0.5意味着其社团内部关联性大于外部关联性,该节点的社团归属已经确定.可能存在对于多个社团的NE值均超过0.5的节点,这部分节点为社团间重叠节点. 步骤13-16考虑社团数量未知的情况下,初始社团数量设置较大,因此根据之前步骤所得重叠节点信息,将符合本文定义的重叠社团合并. 步骤17-20考虑先验信息中的节点对同属信息,若同属节点对中,存在已确定归属社团的节点,则节点对中另一节点也划分至该社团. 步骤21-28处理剩余无社团归属的节点.步骤21-26遍历这部分节点,计算每个节点与相邻社团的NE值,将该节点划分至NE值最大的社团中.若存在节点对同属信息,则划分操作时需考虑该节点的关联节点,将其一并划分至该社团.步骤27-28判断是否仍存在无社团归属的节点,对其进行再次遍历,直至无剩余节点. 最后步骤29返回所得社团划分结果. 本节通过对Zachary 空手道俱乐部网络进行社团划分验证ER-NE算法的有效性.算法首先计算Zachary 空手道俱乐部网络的邻接ER矩阵,如表2所示,计算结果保留两位小数. 表2 空手道俱乐部网络邻接ER矩阵 算法对空手道俱乐部网络的划分结果为2个社团,其中社团1包含的节点集为: (1,2,3,4,5,6,7,8,9,11,12,13,14,17,18,20,22,31) 社团2包含的节点集为: (3,9,10,15,16,19,21,23,24,25,26,27,28,29,30,31,32,33,34) 该划分结果无剩余节点,所得社团数量与实际社团数量相同.与实际社团所包含节点集相比,社团1中多了节点9和节点31,社团2中多了节点3,且这3个节点在2个社团中均有出现,为划分社团所得重叠节点.在实际社团划分中,并未考虑重叠节点,而通过对实际网络的观察,可以发现节点3、节点9以及节点31与2个社团联系均较紧密,可见ER-NE算法对重叠节点的判断比较准确.同时,算法所得社团中的非重叠部分与实际社团一致,因此说明ER-NE算法在考虑节点重叠的同时,保证了社团划分的准确性. 本文进一步对比ER-NE算法和其他经典算法在典型数据集上的实验结果,验证ER-NE算法的优越性.现有加权网络研究采用的典型数据集主要有科学家合作网SCN[20]、PSB数据集[21]、News数据集[22]以及Zachary空手道俱乐部网络.这些数据集中仅PSB数据集和Zachary空手道俱乐部网络具有原始分类信息,因此本文选取这2个数据集作为实验对象.其中PSB数据集为依据三维模型检索系统获得的反馈信息构建的三维模型间的语义关系图,本文具体采用的实验数据集为PSB数据集的一个子集,该子集中含有10个社团. 表3 算法对比结果 数据集算法NANFNWSCPSBWGNFNER-NE10850.631270.6712110.79ZacharyWGNFNER-NE2220.97210.97220.91 在已知的加权网络社团发现算法中,选择经典的WGN算法和FN算法作为对比算法,实验结果如表3所示.表3中NA表示原始数据集中实际社团数量,NF表示算法发现的社团个数,NW表示算法发现的社团中满足弱社团定义的社团数量,SC表示正确划分率.其中正确划分率是将算法所得社团中,不在真实社团中的节点作为错误划分,其余正确划分节点占节点总数的比例.该度量作为衡量算法划分效果的常用方法,适用于社团结构已知的网络.由于ER-NE算法基于本文提出的改进加权网络社团结构定义,因此模块度等常用度量不适合衡量算法的划分效果,所以本文选取正确划分率作为算法对比的衡量指标. 从表3可以看出,ER-NE算法所发现的社团数量与数据集中实际社团数量较为接近,并且所发现的社团符合本文弱社团结构定义的比例更高.由于ER-NE算法的正确划分率的统计考虑了社团间的重叠节点,可能对部分数据集的划分结果正确率数值稍低.若不考虑重叠节点,则算法在PSB以及Zachary数据集上的正确划分率分别为0.87与1.00,与经典算法对比优越性更为明显. ER-NE算法的社团划分结果中,可能包含若干重叠节点.由3.2小节算法描述可知,步骤9-12中可能存在节点对多个社团的有效性NE均大于0.5,即该节点属于多个社团,但有2种情况会造成这些社团之间不发生合并:一是社团数量为已知的固定值,初始社团间不再合并;二是步骤13-16中所示,社团数量未知,但社团间合并后不满足本文定义,因此使得最终划分结果中存在重叠节点.与非重叠社团发现算法相比,ER-NE算法对社团归属较为模糊的节点采取了稳妥的处理,将其看作重叠节点,而不是生硬的将其归属于有效性NE最大的社团.同时,这种处理策略与典型的重叠社团发现算法相比,也存在较大的差异:一是重叠节点的含义不同,ER-NE算法将社团归属较为模糊的节点看作重叠节点,而重叠社团发现算法通常考虑明确同属于多个社团的节点;二是处理对象不同,重叠社团发现研究大多针对无权网络,而ER-NE算法针对加权网络.因此,本文不进一步做二者的具体对比. 本文首先在现有复杂网络社团结构定义的基础上,提出了一种新的加权网络中社团结构定义,在考虑了权重对社团结构影响的同时,综合考虑了节点度对社团结构的作用,并通过在现实网络上的应用,验证了该定义的合理性.然后在本文定义的基础上,结合传统凝聚算法的思想,进一步定义边社团关联性与节点社团有效性指标,提出了一种新的加权网络中社团发现算法(ER-NE算法).该算法利用本文定义的新指标,一方面避免凝聚过程中传递性质出现,另一方面充分体现本文社团定义中对连接权重及节点度的综合考虑.最后选择PSB数据集和Zachary空手道俱乐部网络作为实验数据,与经典WGN算法和FN算法进行了对比实验,实验结果验证了本文算法的有效性和优越性. [1] Newman M E J,Girvan M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69(2):026113. [2] Li Hui-jia,Li Ai-hua,Li Hui-ying.Fast community detection algorithm via dynamical iteration[J].Chinese Journal of Computers,2017,40 (4):970-984. [3] Xie Yi,Sun Yu-qing,Shen Lei.Theme and community evolution in complex social network[J].Journal of Chinese Computer Systems,2016,37(11):2402-2408. [4] Sun Da-ming,Zhang Bin,Zhang Shu-bo,et al.A popularity versus similarity query recommendation strategy[J].Journal of Chinese Computer Systems,2016,37(6):1121-1125. [5] Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2001,99(12):7821-7826. [6] Capocci A,Servedio V D P,Caldarelli G,et al.Detecting communities in large networks[J].Physica A Statistical Mechanics & Its Applications,2004,352(2-4):669-676. [7] Boccaletti S,Latora V,Moreno Y,et al.Complex networks:structure and dynamics[J].Physics Reports,2006,424(4):175-308. [8] Pujol J M,Béjar J,Delgado J.Clustering algorithm for determining community structure in large networks[J].Physical Review E,2006,74(1):016107. [9] Zhang S,Wang R S,Zhang X S.Identification of overlapping community structure in complex networks using fuzzy c-means clustering[J].Physica A,2007,374(1):483-490. [10] Palla G,Derenyi I,Farkas I,et al.Uncovering the overlapping community structures of complex networks in nature and society[J].Nature,2005,435(7043):814-818. [11] Lancichinetti A,Fortunato S,Kertész J.Detecting the overlapping and hierarchical community structure of complex networks[J].New Journal of Physics,2008,11(3):19-44. [12] Jin D,Yang B,Baquero C,et al.Markov random walk under constraint for discovering overlapping communities in complex networks[J].Journal of Statistical Mechanics Theory and Experiment,2011(5):1-11. [13] Evans T S,Lambiotte R.Line graphs,link partitions,and overlapping communities[J].Physical Review E,2009,80(2):016105. [14] Xu Gang,Jin Hai-he,Liu Jing.Community detection based on the opportunistic networks uncertain social[J].Journal of Chinese Computer Systems,2016,37(11):2473-2477. [15] Lv Tian-yang,Xie Wen-yan,Zheng Wei-min,et al.Analysis of community evaluation criterion and discovery algorithm of weighted complex network[J].Acta Physica,Sinica,2012,61(21):145-154. [16] Clauset A,Newman M E,Moore C.Finding community structure in very large networks[J].Physical Review E,2004,70(6):066111. [17] Newman M E J.Analysis of weighted networks[J].Physical Review E,2004,70(5):056131. [18] Newman M E J.Fast algorithm for detecting community structure in networks[J].Physical Review E,2004,69(6):066133. [19] Zachary W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473. [20] Newman M E J.Finding community strcuture in networks using the eigenvectors of matrics[J].Physical Review E,2006,74(3):036104. [21] Lü T,Huang S,Wu P,et al.Researches on semantic annotation and retrieval of 3D models based on user feedback[C].Proceedings of the 6th International Conference on Semantics Knowledge and Grid.IEEE,2010:211-218. [22] Dooley K,Corman S.Dynamic analysis of news streams:institutional versus environmental effects[J].Nonlinear Dynamics Psychology and Life Sciences,2004,8(3):259-284. 附中文参考文献: [2] 李慧嘉,李爱华,李慧颖.社团结构迭代快速探测算法[J].计算机学报,2017,40(4):970-984. [3] 谢 翌,孙宇清,沈 雷.复杂社会网络中主题驱动的社团演化[J].小型微型计算机系统,2016,37(11):2402-2408. [4] 孙达明,张 斌,张书波,等.一种流行性与相似性结合查询推荐策略[J].小型微型计算机系统,2016,37(6):1121-1125. [14] 许 岗,金海和,刘 靖.机会网络的不确定社会关系社团发现[J].小型微型计算机系统,2016,37(11):2473-2477. [15] 吕天阳,谢文艳,郑纬民,等.加权复杂网络社团的评价指标及其发现算法分析[J].物理学报,2012,61(21):145-154.4 实验分析
4.1 ER-NE算法有效性验证
Table 2 AdjacentERmatrix of Zachary network
4.2 ER-NE算法优越性验证
Table 3 Comparison result of algorithms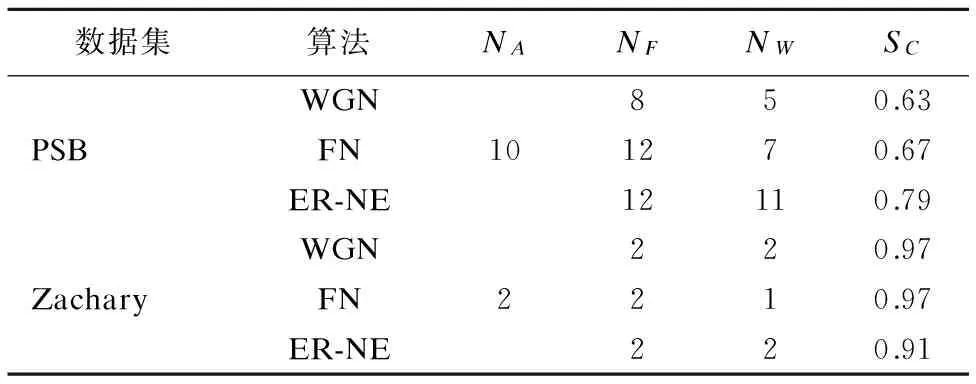
5 总 结

