发电机外部故障切除后励磁调节器动态特性仿真研究
段俊东,陈家林,2,谢芸卉
(1.河南理工大学电气工程与自动化学院,焦作 454000;2.国网河南省电力公司安阳供电公司,安阳 455000)
在电力系统中,励磁调节器是同步发电机励磁系统的重要组成部分,其实质上是一个闭环比例调节器[1-3],它的输入量为发电机机端电压或线路电压,输出量是励磁机的励磁电流或线路电流。当系统出现事故时,控制发电机的励磁控制方式是一种既经济又有效的手段,因此励磁调节器的性能将在很大程度上影响电力系统的安全稳定运行[4-7]。
目前同步发电机的励磁控制系统一般采用自动电压调节器AVR和电力系统稳定器PSS相结合的方式[8-9]。AVR是利用对机端电压的负反馈来保证电压调节的精度,PSS是通过在励磁系统中引入转速、频率等信号,增加系统阻尼来抑制系统振荡。文献[10]指出可将非线性励磁控制器的输出与AVR的输出选用并联接入方式;文献[11]在反馈线性化法设计的非线性励磁调节器中引入电压偏差信号,以改善电压调节精度;文献[12-13]改进了励磁系统的电压闭环控制,引入功角变化量作为偏差信号来修正偏差方程,但其阻尼系数与很多参数有关,很难确定。上述研究都没有考虑自动励磁系统中电流测量值对励磁调节器调整特性的影响。
本文首先对自动励磁调节系统中电流的引入方式进行了分析;然后在Matlab/Simulink下分别建立发电机单机运行和并网运行的仿真模型,对比分析两种仿真模型下励磁调节器的动态特性;并利用戴维南等效电路对励磁调节器中的电流进行了分析;最后结合数字仿真进行了验证。
1 自动励磁系统中电流的引入方式
图1为自动励磁调节系统的原理框图,图2为标准励磁系统模型中的发电机电压与电流测量回路的传递函数[14]。图2中,US为发电机定子电压相量;IS为发电机定子电流相量;RS为调差单元的有功电流补偿系数;Xc为调差单元的无功电流补偿系数;KS和KR为检测环节放大倍数;τR为检测环节时间常数;UREF为发电机电压给定值;UERR为电压偏差。
由图1和图2可看出,自动励磁调节系统引入电流测量值的方式,即电流测量值是发电机定子电流通过电流互感器并经过调差单元以阻抗上的压降的形式被引入到自动励磁调节系统中。通过改变阻抗(RS+jXC)的大小可以使引入的电流测量值的大小发生改变。当系统发生故障时,电流测量值经调差单元作用到励磁系统中,将对发电机励磁控制系统的性能造成影响。

图1 自动励磁调节系统的原理框图Fig.1 Block diagram of the principle of automatic excitation control system

图2 电压信号测量与负载电流补偿模块Fig.2 Module of voltage signal measurement and load current compensation
2 发电机单机运行和并网运行故障切除后励磁调节器的调整特性
2.1 数学模型的建立
同步发电机的数学模型为

励磁系统的数学模型如图3所示。图中:Eef为励磁机出口电压;K为各检测环节的放大倍数;τ为各检测环节的时间常数。

图3 励磁系统数学模型Fig.3 Mathematical model of excitation system
2.2 仿真模型的建立
本文为了研究励磁调节器在发电机单机运行和并网时的调整特性,利用自并励静止晶闸管整流励磁系统,建立了发电机单机运行和并网运行两种仿真模型,发电机单机运行和并网运行时的示意见图4和图5。
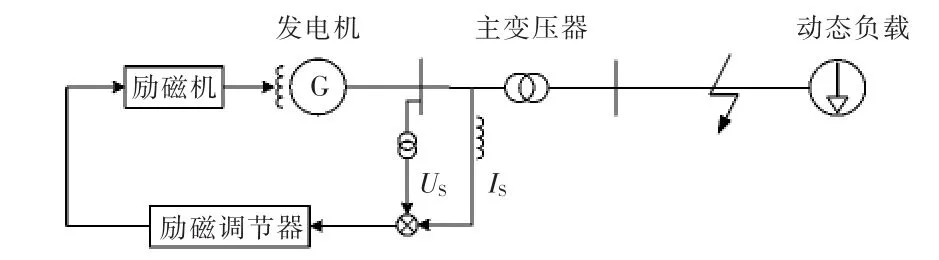
图4 发电机单机运行示意Fig.4 Schematic of generator's unit operation

图5 发电机并网运行示意Fig.5 Schematic of generator's grid connected operation
在图4中,变压器的高压侧接入了动态负载,建立发电机单机运行模型。在图5中,变压器的高压侧接入可近似认为无穷大系统的电源,建立发电机并网运行模型。当发电机单机运行时,将发电机作为平衡节点,进行潮流计算,在给定动态负载下确定了发电机的机械输入功率和励磁输入电压。当发电机并网运行时,将发电机作为PV节点,无穷大系统作为平衡节点,进行潮流计算,确定了发电机的无功功率和励磁输入电压。
在仿真过程中,以单相接地短路、两相短路、两相接地短路和三相接地短路4种故障类型分别进行仿真。鉴于仿真结果受故障类型的影响不明显,故以三相接地短路仿真结果为例做典型说明。以0.1~0.2 s作为故障时间,确保在第一摇摆周期不失稳。
2.3 仿真结果分析
仿真结果选取发电机定子电流响应曲线、机端电压响应曲线、功角响应曲线和励磁电压响应曲线这4个量进行对比研究。仿真结果如图6所示。
由图6(a)可见,当发电机单机运行故障切除后,发电机定子电流几乎没有振荡,在0.22 s后恢复稳定;当发电机并网运行故障切除后,发电机定子电流出现振荡,振荡幅值明显,持续时间较长。
由图6(b)可见,当发电机单机运行故障切除后,发电机端电压出现振荡,振荡幅值不明显,在0.6 s后恢复稳定;当发电机并网运行故障切除后,发电机端电压出现振荡,振荡幅值明显,持续时间较长。

图6 发电机单机运行和并网运行系统响应曲线Fig.6 Response curves of generator's unit operation and grid-connected operation system
由图6(c)可见,当发电机单机运行故障切除后,发电机功角没有出现振荡;当发电机并网运行故障切除后发电机功角出现振荡,振荡幅值明显,持续时间较长。
由图6(d)可见,当发电机单机运行故障切除后,发电机励磁电压出现振荡,振荡幅值不明显,在0.7 s后恢复稳定;当发电机并网运行故障切除后,发电机励磁电压出现振荡,振荡幅值明显,持续时间较长。
综上所述,励磁调节器在发电机单机运行和并网运行时的调整特性不同,且在发电机并网运行故障切除后,发电机端电压、功角、励磁电压均出现振荡,振荡幅值明显,持续时间较长。
3 基于戴维南定理的并网发电机等效电路分析
为了分析发电机并网运行时励磁调节器中电流的变化特性,根据戴维南定理得到了并网发电机的等效电路,如图7所示,图8为其关系矢量。图中,E˙G为发电机电势矢量;E˙S为系统电势矢量;U˙OC为开路等效电压;XG为发电机内部等效电抗;XS为系统等效电抗;回路等效电流即为发电机励磁调节系统中的测量电流。

图7 戴维南等效电路Fig.7 Thevenin's equivalent circuit

图8 矢量关系Fig.8 The relationship of vectors
由图8可知,开路等效电压为

根据矢量分析可知,当E˙G与E˙S同相时,有



式中:fG和fS分别为发电机和系统频率;θ0为发电机与系统的初相差;ωs为转差角频率。
发电机并网瞬间的回路总电抗为

其中XS≈0,故Zin≈XG,因此发电机并网瞬间回路电流为

综上所述,回路电流是一个幅值振荡的交流电流,近似值为开路电压与回路电抗之比,其振荡特性与功角振荡特性相同,该值的引入会加剧发电机与系统间的振荡。
4 仿真验证
为验证当发电机与系统出现振荡时,电流测量值引入励磁调节器后会加剧发电机与系统间的振荡这一结论,仿真模型采用发电机固定励磁电压的方式,即将上述中的固定。由于几乎不变,此时励磁调节器中的电流变化不明显。与发电机自动励磁调压方式进行对比分析,仿真结果如图9所示。
由图9(a)可见,当故障切除后,在固定励磁控制条件下运行的发电机其定子电流振荡效果明显弱于采用自动励磁系统的发电机。
由图9(b)可见,当故障切除后,在固定励磁控制条件下运行的发电机其机端电压没有出现振荡,在自动励磁控制条件下运行的发电机其机端电压出现明显振荡,且持续时间较长。
由图9(c)可见,当故障切除后,在固定励磁控制条件下运行的发电机其功角振荡效果明显弱于采用自动励磁系统的发电机。
综上所述,当故障切除后,在固定励磁电压条件下运行的发电机,其励磁电压为恒定电压,而其定子电流、机端电压和功角振荡效果明显弱于采用自动励磁调压系统的发电机。说明当发电机与系统发生振荡时,电流测量值被引入到励磁控制系统后会加剧发电机与系统间的振荡。
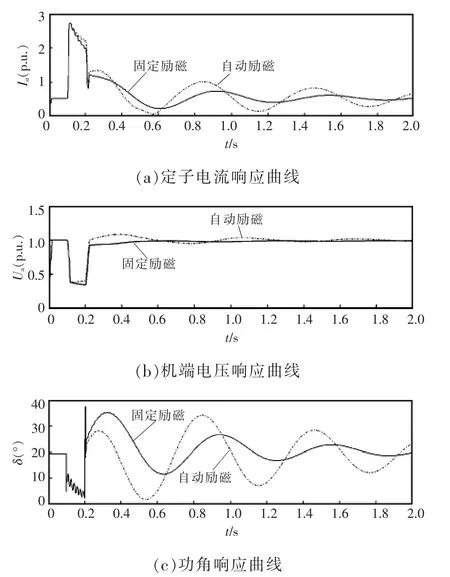
图9 发电机固定励磁运行和自动励磁运行系统响应曲线Fig.9 Response curves of generator's fixed excitation operation and automatic excitation operation
5 结论
(1)通过仿真结果表明,励磁调节器在发电机单机运行和并网运行故障切除后两种调整特性表现不同,且励磁调节器在发电机单机运行时的调整特性比发电机并网运行时的调整特性好。
(2)利用戴维南定理进行理论分析可知,当发电机与系统产生振荡时,引入励磁调节器中的电流为幅值振荡的交流电流,近似为开路电压与回路电抗之比,其振荡特性与功角振荡特性相同。该值的引入会加剧发电机与系统间的振荡。
(3)通过比较固定励磁和自动励磁两种励磁控制方式,发现加装自动励磁调节器的发电机在一定程度上对系统低频振荡有助增的效果,还需进一步研究。
参考文献:
[1]吴跨宇,吴龙,卢岑岑.一种改进型PSS4B电力系统稳定器的工程化应用研究[J].电力系统保护与控制,2015,43(14):113-119.Wu Kuayu,Wu Long,Lu Cencen.Engineering application of an improved PSS4B power system stabilizer[J].Power System Protection and Control,2015,43(14):113-119(in Chinese).
[2]郭琳,王萍,王慧慧.风力发电并网电压扰动信号的分析与检测[J].电源学报,2015,13(5):15-21.Guo Lin,Wang Ping,Wang Huihui.Analysis and detection of transient power quality of wind power grid[J].Journal of Power Supply,2015,13(5):15-21(in Chinese).
[3]舒印彪,汤涌,孙华东.电力系统安全稳定标准研究[J].中国电机工程学报,2013,33(25):1-9.Shu Yinbiao,Tang Yong,Sun Huadong.Research on power system security and stability standards[J].Proceedings of the CSEE,2013,33(25):1-9(in Chinese).
[4]朱方,赵红光,刘增煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报,2007,27(1):1-7.Zhu Fang,Zhao Hongguang,Liu Zenghuang,et al.The influence of large power grid interconnected on power system dynamic stability[J].Proceedings of the CSEE,2007,27(1):1-7(in Chinese).
[5]赵红生,刘源,陈伟彪,等.互联电力系统联络线功率波动机理及其扰动概率分析[J].电力系统保护与控制,2015,43(14):1-9.Zhao Hongsheng,Liu Yuan,Chen Weibiao,et al.Fluctuation mechanism of tie-line active power of interconnected power system and its oscillation probability analysis[J].Power System Protection and Control,2015,43(14):1-9(in Chinese).
[6]王金华,王宇翔,顾云杰,等.基于虚拟同步发电机控制的并网变流器同步频率谐振机理研究[J].电源学报,2016,14(2):17-23.Wang Jinhua,Wang Yuxiang,Gu Yunjie,et al.Synchronous frequency resonance in grid-connected VSCs with virtual synchronous generator technology[J].Journal of Power Supply,2016,14(2):17-23(in Chinese).
[7]匡洪海,张曙云,曾丽琼,等.STATCOM-PSS控制对风电并网系统稳定性和电能质量的改善[J].电源学报,2015,13(3):100-133.Kuang Honghai,Zhang Shuyun,Zeng Liqiong,et al.Stability and power quality improvement of wind power integrated system using STATCOM-PSS control[J].Journal of Power Supply,2015,13(3):100-133(in Chinese).
[8]Demello F P,Concordia C.Concepts of synchronous machine stability as affected by excitation control[J].IEEE Transactions on Power Apparatus and Systems,1969,88(4):316-329.
[9]阮阳,袁荣湘.采用输出反馈方式的电力系统非线性励磁控制[J].中国电机工程学报,2011,31(34):68-76.Ruan Yang,Yuan Rongxiang.Output feedback based nonlinear excitation control for power systems[J].Proceedings of the CSEE,2011,31(34):68-76(in Chinese).
[10]卢强,梅生伟,孙元章.电力系统非线性控制 [M].2版.北京:清华大学出版社,2008:257-295.
[11]孙元章,黎雄,戴和平,等.同时改善稳定性和电压精度的非线性励磁控制器[J].中国电机工程学报,1996,16(5):332-336.Sun Yuanzhang,Li Xiong,Dai Heping,et al.A nonlinear excitation controller to improve both power system stability&voltage regulation accuracy[J].Proceedings of the CSEE,1996,16(5):332-336(in Chinese).
[12]霍成祥,刘取,刘增煌.励磁系统附加调差对发电机阻尼特性影响的机制分析及试验[J].电网技术,2011,35(10):59-63.Huo Chengxiang,Liu Qu,Liu Zenghuang.The analysis and testing of the influence on the damping caused by reactive current compensation[J].Power System Technology,2011,35(10):59-63(in Chinese).
[13]霍成祥,刘取,濮钧.励磁系统中附加调差对电力系统振荡模式阻尼的影响[J].电网技术,2011,35(4):65-70.Huo ChengXiang,Liu Qu,Pu Jun.Impact of reactive current compensation in excitation system on damping of power system oscillation modes[J].Power System Technology,2011,35(4):65-70(in Chinese).
[14]吴跨宇,竺士章.发电机励磁系统调差对PSS参数整定的影响与对策[J].电力自动化设备,2010,30(9):67-71.Wu Kuayu,Zhu Shizhang.Effect of reactive compensation for generator excitation system on PSS parameter setting and solution[J].Electric Power Automation Equipment,2010,30(9):67-71(in Chinese).

