基于支路交换和声搜索算法的配网重构
荣德生,胡举爽,韩淑敏
(辽宁工程技术大学电气与控制工程学院,葫芦岛125105)
配电网络重构包含大量分段开关和少量联络开关[1],具有开环设计、闭环运行的特点。配网重构就是在满足某些条件约束的前提下,对网络中这些开关的状态进行改变,完成对原有网络结构的调整。试着找出一种较优的网络结构组合,从而对配电系统中的潮流进行重新分布,可以使网络运行参数得到优化。依据重构时配电系统所处的运行状态,可以分为正常运行时的网络重构(distribution network reconfiguration)、故障情况下的重构或供电恢复(service restoration)。前者是通过改变分段开关和联络开关的组合状态来改变网络的拓扑结构,以改变网络中的潮流,达到降低网损、提高电压质量和平衡负荷等目的,也是本文主要研究对象;后者是指故障后的隔离故障,缩小停电范围,达到迅速恢复供电的目的。
配网重构需要对网络中的大量开关进行组合优化,因此配网重构是一个多目标非线性混合优化问题,在数学上是一个非确定多项式时间难(NP-hard)问题。实际配电系统规模大、分布广,三相不平衡问题比较突出,在实际操作中网络重构又要达到快速和全局最优的指标,因此,如何解决计算速度和寻优质量二者的矛盾,如何处理配电系统的不对称情况和不确定信息,都是网络重构所面临的难题。目前,适用于配电网进行优化重构的较为普遍的优化算法大致分为4类:数学优化理论方法、最优流模式[2]OPF(optimal flow pattern)法、支路交换法BEM(branch exchange method)和人工智能算法。文献[3]将网络规划的最短路算法应用于配网重构中,利用最短路径法为每个负荷寻找供电路径,方便地形成了树形网络,由于该算法对寻优网络无特殊要求,因此可以容易地用于复杂网络的重构。虽然利用数学优化理论可以得到不依赖于配网初始结构的全局最优解,但存在严重的“维数灾”问题,计算时间较长,难以满足实际需要。结合启发式规则的最优流模式法和支路交换法,虽然能保证重构后配网的辐射性,并能达到降低损耗、平衡负荷的目的,但是计算处理速度较慢,且不能保证得到全局最优解,不适合复杂网络的重构。近年来人工智能的理论和方法在配电网自动化中的应用很广泛。文献[4]采用改进的自适应遗传算法进行配电网的恢复重构,根据含分布式电源的配电网的特点,利用基于环路的编码策略,减少表示孤岛的不可行解;文献[5]提出了一种改进的模拟退火算法,以当前最优解作为当前控制温度下的初始当前解,从而构造了一个单调递减的初始当前解序列,这一改进算法对参数的依赖性更加减小,降低了计算量。但人工智能算法普遍存在依赖初始参数选择和计算量大,容易产生不可行解和陷入局部最优的缺点[6-8]。
针对标准和声搜索算法容易陷入局部最优和产生不可行解的问题,本文采用引入支路交换法的和声搜索算法,对新和声进行局部搜索,生成第2个新和声,增加了和声记忆库的多样性,使得算法能够逃离局部最优,进而提高了算法的全局搜索能力;采用基于环路分解的编码方式对和声编码,保证初始解集中的每个和声都是可行解。
1 配网重构的数学模型
1.1 目标函数
配网重构是一个多目标、多约束的组合优化问题。本文在求解配电系统优化重构问题时,以配网网损和电压偏差最少为目标函数,通过给每个子目标函数赋予不同的权重系数并线性加权求和,使其化为单目标优化问题。用数学函数表示如下:
网络损耗为

式中:f1为目标函数;l为支路编号;n为网络支路总数;rl为支路电阻;kl为支路上开关状态变量,1为闭合状态,0为断开状态;Vl为支路l末端节点电压;Pl和Ql分别为支路l注入的有功功率和无功功率。
节点电压是反映网络供电质量和供电可靠性的重要指标。节点电压偏差是指实际电压幅值与指定电压幅值的偏差,表示为

式中:ΔV为节点电压偏差;Nb为网络节点数;Vi为节点i上的电压幅值;Vrat为指定电压幅值。
则综合优化目标函数为

式中,λ1、λ2为权重系数,λ1+λ2=1。
1.2 约束条件
1)等式约束条件
潮流方程为

其中:Pi、Qi分别为节点i的输入有功功率、无功功率;PDi、QDi分别为节点i处负荷的有功功率和无功功率;Vi、Vj分别为节点 i,j的电压;Gij、Bij和 δij分别为节点i、j的电导、电纳和相角差。
2)不等式约束
支路电流及节点电压约束为

式中:Vjmin、Vjmax为节点 j电压的上下限值;Ii为流经支路电流值;Iimax为流经支路i的电流上限值。
3)网络拓扑结构约束
保持配电网络放射状运行的结构特征,重构后不应有孤岛存在。
4)开关操作次数限制
为延长开关使用寿命,尽量减少配网重构过程中开关重复操作的次数。
2 支路交换和声搜索算法
2.1 HSA简介
标准和声搜索算法HSA(harmony search algorithm)最早是以Geem等音乐人即兴演奏最优美和声为理论依据提出的。算法模拟了音乐创作中乐师们凭借自己的记忆,通过反复调整乐队中各乐器的音调,最终达到一个美妙的和声状态的过程[9]。HSA将乐器声调的和声类比于优化问题的解向量,评价即是各对应的目标函数值。文献[10]对演奏者弹奏音乐的过程和工程寻优迭代过程进行了对比,解释了二者的内在联系,即音乐人进行演奏的乐器对应工程问题中的决策变量,弹奏乐器的音调对应决策变量的值域。每种乐器演奏出的音调组合层整体形成一个和声,类似目标函数值对应的变量。音乐家通过一次次的演奏练习发现最美和声,相应地,多个决策变量构成一个解向量,计算出解向量对应的目标函数值,比较并将较优解存储在解集中,继续完成工程寻优。和声搜索算法的参数分析如下。
和声记忆库大小HMS(harmony memory size)表示有HMS个个体存储在HM中。HMS较大时有利于提高算法的全局寻优性能,但同时会因计算繁杂降低算法的寻优效率;HMS过小则无法保证提供充足的采样从而降低算法的寻优性能。
音调微调概率 PAR(pitch adjusting rate)的值域为0≤PAR≤1。减小PAR值会导致算法极易陷入局部寻优搜索;增大PAR值能够减少HSA极易收敛于局部寻优的概率。
和声记忆库取值概率HMCR(harmony memory considering rate)的值域是0≤HMCR≤1。一般情况下选取较大的HMCR值,即0.9≤HMCR≤1。
迭代次数 NI(iteration number)指算法迭代次数,即算法进行工程寻优时的迭代停止标准。
2.2 支路交换HSA简介
通过分析算法参数的意义发现,HSA是基于HMCR、PAR、HMS等参数取值的智能优化方法,其寻优效果对参数值具有很大的依赖性。所以,在和声搜索算法的寻优过程中,如果参数选取不合理,将会导致算法收敛性能差、极易陷入局部最优等。为了降低算法寻优结果对初始参数的依赖性,弥补HSA局部寻优的不足,本文采用快速支路交换法进行局部寻优搜索,并且把算法局部搜索产生的新解经过适应度函数值的计算比较,参与和声记忆库的更新。快速支路交换法在网络重构时忽略对潮流分布的计算,进而加快了算法的运算速率。通过比较最佳转移负荷的数值和正负号对单环路的最大降损开关进行判别,极大地缩小了搜索范围。
根据适应度函数值(适应度值)来判定算法的寻优方向,同时规定目标函数的优化方向与适应度值增加的方向是一致的。适应度值在和声搜索算法中作为区别和声记忆库中和声好坏的标准,反映和声能够达到或者接近最美和声状态 (全局最优方案)的优良程度,同时也是更新HM的重要依据。
通常把优化问题的目标函数作为最常用的适应度函数,适应度函数表示为

式中:F1为网络损耗指标;F2为节点电压偏差指标。
2.3 算法流程
基于支路交换的HSA在配网重构中的实现流程如图1所示。算法应用的实现步骤如下。
步骤1输入配电网络的基本数据。
步骤2设置算法参数。设置初始解集的规模M、和声编码的长度L、最大迭代次数NI、HMCR、HMS和PAR。
步骤3采用基于环路分解的编码方式对开关进行编码,并且产生由M个个体组成的初始解集Q,完成对初始和声解集的初始化。
步骤4采用基于支路电流的前推回代法求解配电系统中的潮流分布,并记录各支路的有功和无功功率。
步骤5计算初始解集中个体的适应度值的大小,对适应度函数值排列时遵照降序原则,选出排在前HMS的和声,存入和声记忆库HM,初始化和声记忆库。
步骤6按照标准HS搜索算法即兴创作第1个新和声,采用结合启发式规则的支路交换法进行局部搜索生成第2个新和声。

图1 支路交换HSA的配网重构流程Fig.1 Flow chart of distribution network reconfiguration based on branch exchange HSA
步骤7求解新生成和声的适应度函数值并对其进行判断。当比HM中最差和声更优时,则用新和声替换HM中的最差和声,并将新和声存放到HM内;否则,保持HM中原有的和声不变。
步骤8校验是否达到算法寻优时设定的迭代运算的终止条件。当计算的迭代计数个数达到NI时,则终止运算过程;否则,继续重复步骤5~7。
3 算例分析
图2为IEEE33节点系统的网架,总负荷为3 715 kW+j2 300 var,基准功率值为10 MVA。网络中包含33个节点、37条支路和5个联络开关,实线为网络中分段开关的所在位置,虚线为网络中联络开关所在的位置。为了验证本文方法的有效性与可行性,分别用本文方法、文献[9]标准和声搜索算法和文献[11]遗传算法对上述配电网进行网络重构。
根据本文基于环路分解的编码方式,设置和声编码长度L=5、M=50、HMS=10、HMCR=0.9、PAR=0.4、NI=50,目标函数中 λ1=0.6,λ2=0.4。
重构前 (图2),IEEE 33节点配电系统中支路8-21、9-15、12-22、18-33 和 25-29 是处于断开状态的,系统的有功损耗为202.66 kW,节点最低电压为0.913 1p.u.(节点18处)。在MATLAB2012a的语言环境下,运用本文算法对此网络重构后(如图3),网络中断开的支路为 7-8、9-10、14-15、25-29和 32-33(为最优结构),此时系统有功损耗是139.50 kW,最低电压为0.938 0 p.u.(节点32处)。重构对比分析结果见表1。

图2 IEEE 33节点配电网络Fig.2 IEEE 33 nodes distribution network

图3 重构后的IEEE 33节点配电系统结构Fig.3 Structure of the IEEE 33 nodes distribution system reconstruction

表1 IEEE 33节点配电网络重构后的对比结果Tab.1 Comparison results of IEEE 33 nodes distribution network reconstruction
为了验证本文算法的寻优效率,连续测试本文算法和文献[9]、文献[11]算法各100次,将算法性能指标进行对比分析。为了比较算法的全局收敛性,定义全局寻优率η为

式中:RB为得到全局最优结果的次数;RN为总运行次数。
算法性能比较如表2所示。由表1和表2可知,对于IEEE 33节点系统,本文方法得到全局最优结果所需的最小、最大和平均迭代次数分别为2次、190次和84次。相比文献[9]的标准HS算法和文献[11]遗传算法,本文算法的迭代次数明显要小,且全局寻优率达到99%,远远高于文献[9]标准HS算法的21%。由此可知,本文算法收敛性要优于文献[9]标准HS算法,并且全局寻优率也更高。这是因为通过引入结合启发式规则的支路交换法进行“局部搜索”,局部搜索和全局搜索相结合能使算法有效逃离局部最优,并改善算法的全局收敛性能,所以本文算法的收敛速率较快,全局最优解的搜寻性能更高、更好。和文献[11]中的遗传算法性能比较,本文算法稳定性更高,收敛速度也更快。另外,对于IEEE 69节点系统,利用本文算法得到最优结果所需的最小、最大和平均迭代次数分别为2次、198次和106次,与IEEE 33节点系统相近,故本文算法稳定性好,收敛速度不随节点规模变大而变差。
在IEEE 33节点配电网络重构前后的电压分布如图4所示。从图4及表1可知,仿真结果表明,采用本文算法得到的网损和目标函数值最低,节点电压偏差最小,由202.66 kW减少到139.50 kW,比初始网络网损减少31.2%,提高了配电网运行的经济性;最低节点的电压从0.913 1 p.u.上升至0.938 6 p.u.,改善了配电网络中各个节点的电压分布情况,提高了供电电压的质量。
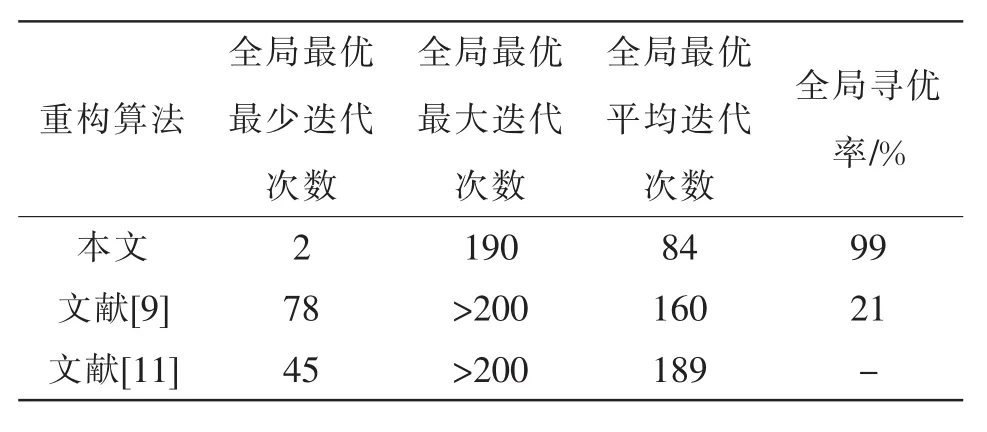
表2 算法性能比较Tab.2 Comparison of performance among different algorithms
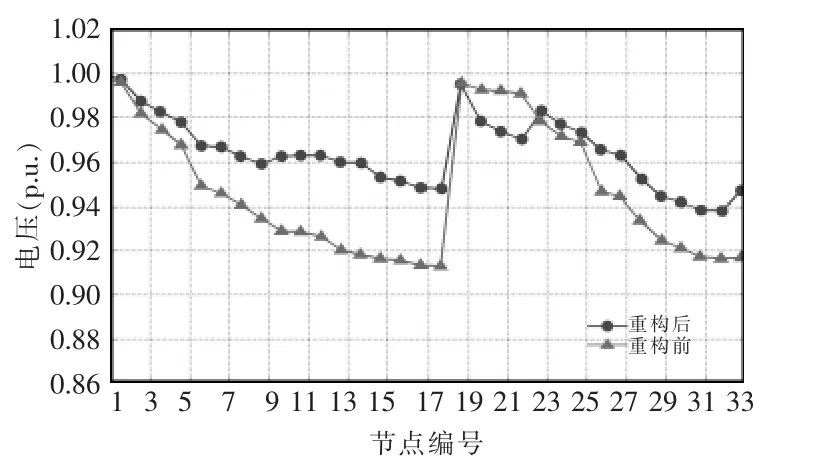
图4 电压分布Fig.4 Distribution of voltage
4 结语
针对标准和声搜索算法容易陷入局部最优和产生不可行解的问题,本文采用引入支路交换法的和声搜索算法,对新和声进行局部搜索,生成第2个新和声,增加了和声记忆库的多样性,使得算法能够逃离局部最优,进而提高了算法的全局搜索能力。采用本文算法对典型IEEE33节点配电网络进行了重构,结果表明,引入支路交换的和声搜索算法并利用启发式规则指明有效搜索方向,缩小了重构的寻优范围,增大了有效解的概率,提高了算法的搜索效率,具有良好的寻优性,且不受初始参数值的影响,搜索性能不随网络规模的扩大而变差,是求解配网重构问题的一种较好算法。通过比较重构前后的结果,发现最低节点电压得到升高,改善了系统的供电质量;网络的损耗有效降低,减少了网络运行的成本。
但本文算法中,虽然加入局部搜索提高了算法的寻优性能,但同时也延长了算法运行时间,对此还需继续改进。另外,本文主要针对配电系统正常运行时的重构问题进行了探究,而对于配电系统处于故障状态时如何优化重构网架,从而达到快速恢复供电的效果的问题有待进一步研究。
参考文献:
[1]刘健,毕鹏翔,董海鹏.复杂配电网简化分析与优化[M].北京:中国电力出版社,2002.
[2]邓佑满,张伯明,相年德.配电网络重构的改进最优流模式算法[J].电网技术,1995,9(7):47-50.Deng Youman,Zhang Boming,Xiang Niande.An improved optimal flow pattern algorithm for distribution network reconfiguration[J].Power System Technology,1995,19(7):47-50(in Chinese).
[3]余贻鑫,段刚.基于最短路算法和遗传算法的配电网络重构[J].中国电机工程学报,2000,20(9):45-50.Yu Yixin,Duan Gang.Shortest path algorithm and genrtic algorithm based distribution system reconfiguration[J]Proceedings of the CSEE,2000,20(9):45-50(in Chinese).
[4]胡雯,孙云莲,张巍.基于改进的自适应遗传算法的智能配电网重构研究[J].电力系统保护与控制,2013,41(23):85-90.Hu Wen,Sun Yunlian,Zhang Wei.Reconfiguration of smart distribution using improved adaptive genetic algorithm[J].Power System Protection and Control,2013,41(23):85-90(in Chinese).
[5]胡敏羑,陈元.配电系统最优网络重构的模拟退火算法[J].电力系统自动化,1994,18(2):24-28.Hu Minyou,Chen Yuan.Simulated annealing algorithm of optimal reconstruction in distribution system[J].Automation of Electric Power Systems,1994,18(2):24-28(in Chinese).
[6]Das D.A fuzzy multi-objective approach for network reconfiguration of distribution systems[J].IEEE Transactions on Power Delivery,2006,21(1):202-209.
[7]葛少云,刘自发,余贻鑫.基于改进禁忌搜索的配电网重构[J].电网技术,2004,28(23):22-26.Ge Shaoyun,Liu Zifa,Yu Yixin.An improved Tabu search for reconfiguration of distribution systems[J].Power System Technology,2004,28(23):22-26(in Chinese).
[8]Irving M R,Luan W P,Daniel J S.Supply restoration in distribution networks using a genetic algorithm[J].International Journal of Electrical Power and Energy Systems,2002,24(6):447-457.
[9]Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation Transactions of the Society for Modeling&Simulation International,2001,76(2):60-68.
[10]Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems[J].Applied Mathematics and Computation,2007,188(2):1567-1579.
[11]邓永生.遗传算法在配电网重构中的应用研究[D].重庆:重庆大学,2002.

