电网对称故障下无刷双馈电机低压穿越分析

于 洋，侯晓鑫

（天津大学电气自动化与信息工程学院，天津300072）

随着风力发电技术的快速发展，电网中风机容量比重越来越大，风电机组对电网系统稳定性的影响也愈加显著。为此，国家电网公司不断规范风电场接入电网技术规定，其中针对风电机组在电网电压跌落时能够保持不脱网运行，即低电压穿越LVRT（low-voltage ride-through）能力备受关注。

无刷双馈电机BDFM（brushless doubly-fed machine）应用在变速恒频风力发电系统中，独特优势表现在：没有电刷和滑环，维护成本低，结构简单可靠；所需变频器容量小，可以实现小功率控制大功率；励磁能量能够双向流动。无刷双馈风力发电系统如图1所示。

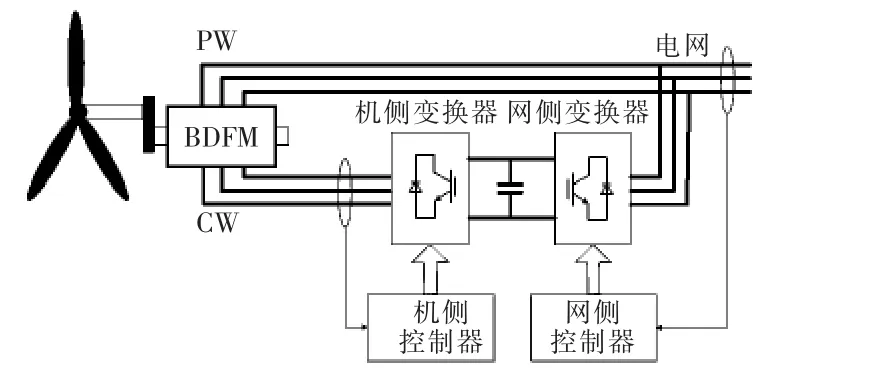
图1 无刷双馈风力发电系统机组Fig.1 BDFM wind power generator system

目前，国内外针对无刷双馈电机LVRT的研究较少[1-2]。文献[1]首次分析研究BDFM的低压穿越，提出2种提高BDFM低压穿越能力的方法，即增加Crowbar保护装置（撬棒保护电路）和串联动态电阻SDR（series dynamic resistance）电路，在电网电压对称跌落时，BDFM低压穿越能力能够有所改善；文献[2]对双馈感应发电机和无刷双馈感应发电机BDFIG（brushless doubly-fed induction generator）进行了对比研究，分析了两种电机的相同点和不同点，比较两电机机侧控制器无功功率外环和转速外环控制策略。在电压跌落期间，比较两电机的磁链幅值、定子电流、转矩、有功和无功功率，仿真和实验结果表明BDFIG的低压穿越能力优于DFIG（doubly fed induction generator）。

关于反馈线性化的研究，20世纪90年代曾有学者提出了异步电机的反馈线性化控制[3]，但研究发现异步电机的反馈线性化方法与已普遍采用的磁场定向矢量控制系统的实现方案相同。文献[4]应用输入输出反馈线性化解决BDFM的解耦控制问题，实现了电机转矩和磁链之间的解耦控制。

本文针对无刷双馈发电机组机侧控制器应用输入输出反馈线性化解耦控制策略。在电网电压三相对称跌落下，推导控制电机定子暂态电流和控制电机定子反电动势暂态方程，分析BDFM的暂态响应。推导得出BDFM稳定运行时，控制电机转子磁链与功率电机定子电压满足线性比例关系。由此给出在电网电压三相对称跌落下BDFM能够保持稳定运行的低压穿越模式。仿真结果证明了理论分析的正确性和有效性。

1 BDFM数学模型

无刷双馈电机按转子结构分为绕线式、鼠笼式和磁阻式，本文仅以绕线式无刷双馈电机为例进行说明，绕线式无刷双馈电机的数学方程可以根据级联无刷双馈电机得到。级联无刷双馈电机结构如图2所示，它由2台绕线式异步电机同轴串联而成，其2套转子绕组反相序连接，省去了电刷和滑环。2台异步电机分别为极对数为pP的功率电机和极对数为pc控制电机，功率绕组接恒定电压，控制绕组接变频器，两套绕组间通过转子磁场耦合实现能量的传递。

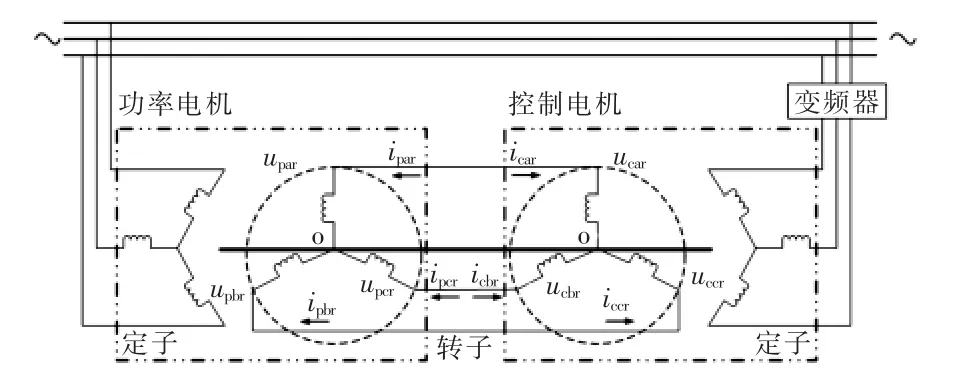
图2 级联无刷双馈电机结构Fig.2 Structure of cascade BDFM

文献[5-6]推导出无刷双馈电机在转子dq坐标系下的电压、电流数学模型为

磁链方程为

式中：下标c和p、r和s、P分别表示控制电机和功率电机、转子和定子、电机极对数；r、lm、l分别为电阻、互感、电感；ωr为转子机械角速度；d为微分算子；和分别为电流矢量和磁链矢量；为功率电机定子电压矢量，为控制电机定子电压矢量，。

BDFM稳定运行时，由于两套转子绕组反相序连接的特殊结构，使得控制电机和功率电机转子电流大小相等，相序相反，即控制电机和功率电机相关矢量相对转子的旋转角速度大小相等，方向相反。如果将dq坐标系下的数学模型直接变换到任意坐标系下，电机数学模型中将会存在转差角的三角函数[4-6]。类似统一坐标系方法[7]，以控制电机为基准，取，如图3所示，将功率电机矢量进行负共轭转换，得到旋转方向相反的新矢量，即。功率电机新矢量与控制电机矢量相对转子坐标系的旋转角速度大小相等，方向相同。控制电机新矢量与功率电机矢量之间保持相对静止，为电机控制策略的分析和研究带来便利。

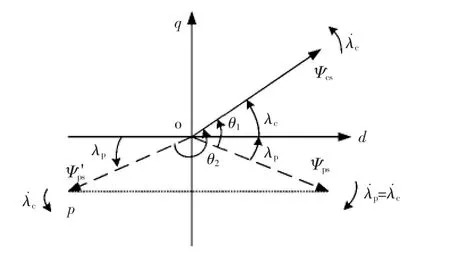
图3 BDFM矢量变换关系Fig.3 Vector transformation relationship in BDFM

变换后BDFM在转子dq坐标系下的数学模型为

磁链方程

电磁转矩方程和运动方程分别为

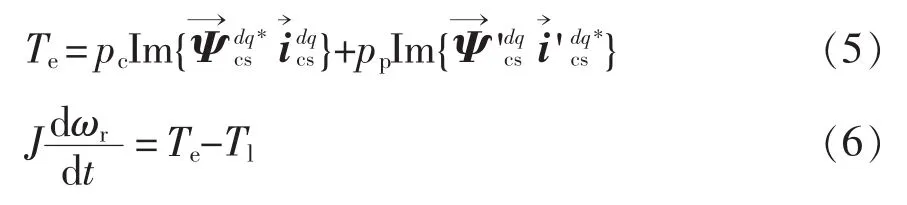
转子坐标系下控制电机和功率电机各变量都是交流量而非直流量，不利于对系统进行分析，且直接应用PI控制器难以消除静态误差，因此需要将转子坐标系下BDFM的数学模型转换到控制电机同步坐标系下。转子坐标系与控制电机同步坐标系之间的关系如图4所示，图中λc为控制电机同步坐标系与转子坐标系之间的夹角。

转子坐标系转换到控制电机同步坐标系下的变换关系

图4 控制电机转子坐标系与同步坐标系的关系Fig.4 Relationship between the rotor reference frame and the synchronous reference frame of control machine

将式（7）代入BDFM的转子坐标系模型中，可得控制电机同步坐标系下电压方程、磁链方程、转矩方程分别为

其中定义等效控制电机转子磁链

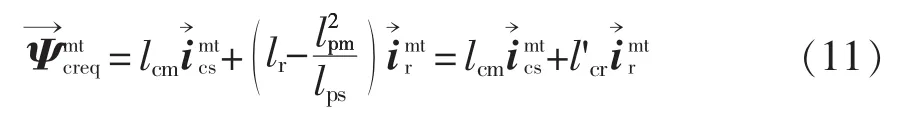
文献[4]中给出了无刷双馈电机在控制电机转子磁场定向的同步坐标系下的状态空间方程。以控制电机转子磁链和电磁转矩为系统的输出变量，系统的仿射非线性形式可以写成

2 BDFM反馈线性化控制方法

文献[4]使用无刷双馈电机的输入输出反馈线性化控制方法来实现BDFM的解耦控制，简述如下。

由式（12）和式（13）可得系统输出表示为

根据反馈线性化理论，系统输出Ψcreq的相对阶为1，Te的相对阶为0。

为了实现输入输出反馈线性化，需要定义一个新的控制输入v，表示为

当D（x）非奇异时，系统可以进行输入输出反馈线性化控制，令

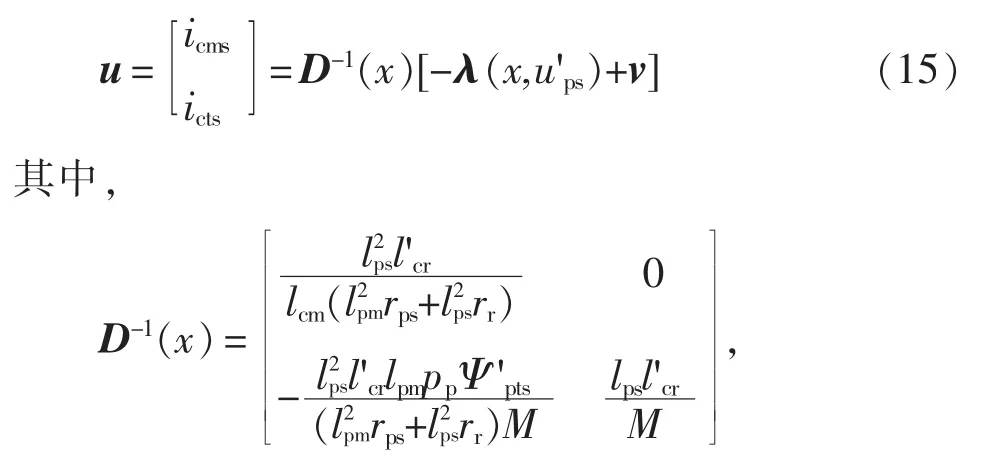
M=lcm（pclpsΨcreq-pplpmΨ 'pms）。则反馈线性化后系统为

可见系统的输出变量与新的输入变量具有线性的、解耦的映射关系。

系统实现反馈线性化的前提条件是矩阵D（x）非奇异，为满足上述要求，可以推导出控制电机转子磁链幅值满足条件为

3 BDFM低压穿越模式

忽略转子电阻，由式（8）、式（9）可以得到

将式（18）代入式（9），可得新磁链方程为

在电网电压发生三相对称跌落故障的极短时间内，忽略电网电压跌落时自身振荡的过程[2]，功率电机定子电压会随着电网电压的跌落而发生跌落，由，忽略定子电阻上的压降，可得

在电网电压发生故障后，会在功率电机定子磁链中产生瞬间的直流分量和交流暂态分量。电机定子磁链将以工频50 Hz衰减振荡，并最终逼近于故障后电压条件下的新的稳态工作点，则有

式中：δ0为功率电机定子磁链衰减系数，与功率电机定子电阻和定子电感相关；ωp为振荡频率。

将式（21）代入式（8），可得

可见，功率电机定子磁链的变化会使得控制电机定子电流也发生变化。由式（21）和式（22）可得电网电压三相对称跌落下控制电机定子电流为

由式（23）第1项可以看出，在电网电压发生三相对称故障，控制电机定子电流也会产生暂态交流分量，振荡频率和衰减系数与功率电机定子磁链相同。电网电压跌落幅值越深，引起的控制电机定子电流暂态分量的幅值越高。

由式（8）、式（19）、式（22），忽略转子电阻，有

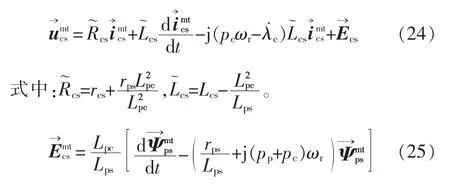
因而可以得到BDFM控制电机定子侧瞬态等效电路[1]，如图5所示。

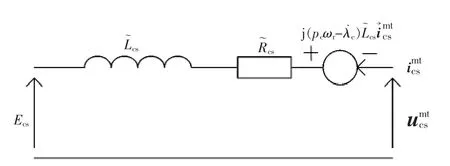
图5 控制电机定子侧瞬态等效电路Fig.5 Stator transient equivalent circuit of control machine

将式（21）代入式（25），忽略功率电机定子电阻，可以得到电网电压三相对称跌落下控制电机定子反电动势方程为

在电网电压三相跌落过程中，控制电机定子反电动势交流暂态分量的幅值一般远高于直流稳态分量的幅值，而且电机转速越快或电网电压跌落幅度越大，引起的控制电机定子反电动势越大，当交流暂态分量幅值高于中间直流母线电压时，会引起控制电机定子过电流，对控制系统稳定性产生影响，严重时会出现故障。

采用输入输出反馈线性化控制方法的优点在于消除了磁链和转矩间的耦合影响，系统响应速度快，实现了系统的高性能解耦控制。为了降低控制电机定子电流脉动，提高BDFM的低压穿越能力，在应用输入输出反馈线性化控制方法的基础上，采用低压穿越控制模式。

在稳态下，由式（11）可得

结合式（20）、式（22）和式（27），可以得到在BDFM稳定运行时，控制电机转子磁链与功率电机定子电压满足线性比例关系为

BDFM输入输出反馈线性化解耦控制框图如图6所示。

图6 反馈线性化控制框图Fig.6 Block diagram of feedback linearization control

4 仿真验证

在MATLAB/Simulink环境下搭建BDFM发电系统机组仿真模型。为了保证仿真中的BDFM与实际中的无刷双馈电机一致，选用电机参数如下。

功率绕组：极对数pp=1，电阻rps=1.77 Ω，电感lps=0.461 H，互感lpm=0.457 5 H；控制绕组：极对数pc=3，电阻rcs=1.64 Ω，电感lcs=0.136 H，互感lcm=0.115 H；转子绕组：电阻rr=6.002 8 Ω，电感lcr=0.597 H，转动惯量：J=0.01 kg·m2；额定电压 380 V，额定电流9.8 A，电机功率3.73 kW，额定转速900 r/min。

在仿真实验中，控制电机磁链给定为0.8 Wb，电机转速给定值为400 rpm。电网电压在0.5 s时三相对称跌落30%。BDFM在电网电压30%跌落条件下，不采用和采用低压穿越模式的仿真结果如图7和图8所示。

不采用低压穿越模式的仿真结果如图7所示。在0～0.5 s范围内，图（a）为功率电机定子相电压波形，功率电机定子电压保持220 V/50 Hz；由图（b）和图（c），控制电机转子磁链和电机转速都能跟踪给定值，分别稳定在0.8 Wb和400 rpm；由图（d）、（e）和（g），控制电机定子电流和功率电机定子电流都能保持稳定，中间直流母线电压稳定在380 V，说明在对BDFM应用输入输出反馈线性化控制方法时，电机能够保持稳定运行状态。

在0.5 s时电网电压对称跌落30%，由图7（b）和（c）可以看出控制电机转子磁链和电机转速大范围振荡，不能保持稳定状态；由图7（d）和（e），控制电机定子电流最大冲击峰值达到约34 A，功率电机定子电流最大冲击峰值达到约25 A，且均在大范围内振荡，控制电机和功率电机定子绕组不能承受如此高的过电流，可能会烧毁电机；由图7（g），中间直流母线电压同样在大范围内振荡不能保持稳定。由此可以看出，在电网电压对称跌落30%时，不采用低压穿越模式的BDFM达不到低压穿越规定的要求。

采用低压穿越模式的仿真结果如图8所示。在0～0.5 s范围内，控制效果与图7相同，在此不做赘述。在0.5 s检测到电网电压三相对称跌落30%时，给定控制电机转子磁链相应减小30%，即给定磁链由 0.8 Wb变为 0.56 Wb，如图8（a）所示；由于所采用的输入输出反馈线性化解耦控制方法的有效性，系统响应很快，控制电机转子磁链很快跟踪新的给定值，电机转速依旧稳定在400 rpm；由图8（c）和（d），在低压穿越模式下，可以看到控制电机定子电流和功率电机定子电流在0.5 s时会出现一个尖峰，即电压跌落瞬间引起的暂态电流；在0.5 s后控制电机定子电流和功率电机定子电流能快速过渡到新的稳态值，电机继续保持稳定运行状态；由图8（f），对于中间直流母线电压，在低压穿越下也能够保持很好的稳定状态。

图7 电网电压30%跌落下仿真波形Fig.7 Simulation waveforms under 30%grid voltage dip

图8 电网电压30%跌落下低压穿越模式仿真波形Fig.8 Simulation waveforms in LVRT mode under 30%grid voltage dip

5 结语

本文在已有输入输出反馈线性化解耦控制策略的基础上，推导分析了电网电压三相对称跌落时控制电机定子暂态电流和控制电机定子反电动势暂态方程，分析BDFM的暂态响应，给出了BDFM在低压穿越下能够稳定运行的方法，仿真结果验证了方法的正确性。

参考文献：

[1]Long Teng,Shao Shiyi,Malliband P.Crowbarless fault ride-through of the brushless doubly fed induction generator in a wind turbine under symmetrical voltage dips[J].IEEE Transactions on Industrial Electronics,2013,60（7）:2833-2841.

[2]Tohidia S,Tavnerb P,McMahonc R.Low voltage ridethrough of DFIG and brushless DFIG:Similarities and differences[J].Electric Power Systems Research,2014,110（5）:64-72.

[3]阮毅,陈伯时,江明.矢量控制系统是异步电动机非线性解耦控制的一类实现[J].电气传动,1993（6）:2-8.Ruan Yi,Chen Boshi,Jiang Ming.Vector control system—A class of realization of nonlinear decoupling control of induction motors[J].Electric Drive,1993（6）:2-8（in Chinese）.

[4]Xia Chaoying,Guo Haiyu.Feedback linearization control approach for brushless doubly-fed machine[J].International Journal of Precision Engineering and Manufacturing,2015,16（8）:1699-1709.

[5]Li Ruqi,Wallace A K,Spee R,et al.Two-axis model development of cage-rotor brushless doubly-fed machines[J].IEEE Transactions on Energy Conversion,1991,6 （3）:453-460.

[6]王乐英,夏超英.级联无刷双馈电机的磁场定向直接反馈控制[J].中国电机工程学报,2011,31（30）:132-139.Wang Leying,Xia Chaoying.Field-oriented direct feedback control of cascaded brushless double-fed machine[J].Proceedings of the CSEE,2011,31（30）:132-139（in Chinese）.

[7]Poza J,Oyarbide E,Roye D,et al.Unified reference frame dq model of the brushless doubly fed machine[J].IEE Proceedings:Electric Power Applications,2006,153（5）:726-734.

[8]张禄,金新民,唐芬,等.电网电压对称跌落下的双馈感应发电机PI-R控制及改进[J].中国电机工程学报,2013,33（3）:106-116.Zhang Lu,Jin Xinmin,Tang Fen,et al.Improved PI-R control for doubly fed induction generators under grid voltage symmetrical dip[J].Proceedings of the CSEE,2013,33（3）:106-116（in Chinese）.

[9]Hu Jiabin,He Yikang,Xu Lie,et a1.Improved control of DFIG systems during network unbalance using PI_R current regulators[J].IEEE Transactions on Industrial Electronics,2009,56（2）:439-451.

[10]Sato Y,Ishizuka T,Nezu K.A new control strategy for voltage-type PWM rectifiers to realize zero steady-state control error in input current[J].IEEE Transactions on Industry Applications,1998,34（3）:480-486.