肿瘤特征基因选择的互信息最值过滤原则与粒子群优化算法

喻德旷，杨　谊

(南方医科大学 生物医学工程学院，广州 510515)(*通信作者电子邮箱yiyang20110130@163.com)

0　引言

随着基因芯片技术的发展，目前已经可以利用基因表达谱对肿瘤进行分子识别、分型，查找肿瘤标志物。基于少量样本(样本量<100)，基因芯片技术能够产生大量基因(基因量>10 000)，但仅有少量基因与肿瘤的发生密切相关，称为特征基因(Feature Genes)，其他非特征基因称为管家基因(House-keeping Genes)[1]。从大量基因中选取有效可靠的特征基因，去除管家基因，是进行正常组织与肿瘤组织区别以及肿瘤亚型分类的关键[2]，特征基因的准确筛选能够减轻分类器的计算负担，提高分类准确度和效率。在此基础上还可以提示分子生物学实验方向，帮助发现肿瘤的新分型以及新的肿瘤生物标记[1-2]，因此，特征基因选择是肿瘤识别与分类问题的研究重点。

基因数据小样本、高维数、高冗余的特点容易导致“维数灾难”(Curse of Dimensionality)和“过拟合”(Over-fitting)[3]。目前有许多文献对特征选择算法作了探索，常见的特征选择算法主要分为三种类型：过滤法(Filter)、封装法(Wrapper)和嵌入法(Embedded)[3]。过滤法是按照某种原则直接排除掉不满足条件的基因，保留最符合条件的若干基因，例如：文献[4]采用t-test过滤法；文献[5]比较了信噪比、Fisher Ration等过滤法的机制。这一类方法的优点是选择结果独立于分类算法模型，简单快速，计算量小，算法过程容易实现；但过滤法算法往往基于单个基因进行指标计算，没有考虑到基因之间的相关性[6]。封装法指定分类器，以启发式算法逼近最优解来寻找特征基因集合，通常的做法是直接利用分类算法来评估特征基因子集，例如：文献[7]采用支持向量机(Support Vector Machine， SVM)方法通过递归特征消除获得白血病和肠癌数据的特征基因子集；文献[8-9]采用粗糙集提取基因数据中的属性，获得特征基因子集；文献[10]提出了一种优化的邻域粗糙集的混合基因选择算法。这一类方法可对不同的分类器选出自适应特征子集，但算法实现较为复杂，计算代价较高，容易产生过拟合，容易受噪声干扰。嵌入法是将特征选择算法嵌入到学习算法中，例如：文献[11]采用ReliefF+SVM法挑选出排序靠前的若干个基因作为特征基因，再使用SVM选择法进一步对这些特征基因进行递归排序；文献[12]采用基于SVM的直推式学习法选择特征基因；文献[13]提出了一种融合0/1随机矩阵替换与SVM的基因选择方法。这类方法能与分类器较好地耦合，但算法复杂，需要结合具体数据处理多种特定情况，并且选择结果对分类器依赖性大。

为了提高特征基因提取的准确率和效率，并使海量复杂医学数据的处理变得简便，本文尝试将群体智能算法与改进的过滤法的优势相结合，进行特征基因选择。近年来兴起的群体智能算法逐渐被用于复杂数据的处理，这是一类仿生启发式算法，通过模仿昆虫、兽群、鸟群和鱼群的群集行为，利用群体智慧进行协同搜索，群体按照合作的方式寻找目标，群体中的每个成员通过自身的经验和学习其他成员的经验来不断地改变搜索的方向[14]，在解空间内找到最优解。粒子群优化(Particle Swarm Optimization， PSO)算法是一种出色的群体智能算法，它利用群体中的个体对信息的共享，使整个群体的运动产生从无序到有序的演化过程，从而在问题求解空间中获得最优解。PSO是一种并行算法，适合解决数据计算量巨大的问题[15]，具有易实现、不受解空间限制性假设的约束等优点，但容易产生局部收敛，得不到全局最优解，因此出现了大量的改进研究，如：文献[16]提出了自适应PSO算法，通过评价迭代过程中每个粒子的性能来改善结果；文献[17]提出了具有完全学习策略的量子行为粒子群(Quantum-behaved Particle Swarm Optimization algorithm based on Comprehensive Learning strategy, CLQPSO)算法，在迭代更新时能充分利用所有粒子当前最佳位置所提供的社会信息，并通过粒子间的社会合作丰富种群的多样性，提高算法在求解多峰问题时的全局收敛性能；文献[18]利用二进制PSO算法与抗早熟的遗传算法相结合提出了二进制粒子群优化与防治基因算法(Binary Partical Swarm Optimization and Combat Genetic Algorithm, BPSO-CGA)，实现了较好的特征基因选择效果。

1　特征基因选择算法设计思路

基于以上分析，本文首先借鉴过滤法思路简单、实现容易的优点，改进其只考虑单变量因素的缺点，将基因之间以及基因与类别之间的关联关系考虑进来，对候选基因进行初步筛选，得到一个尽可能包含更多特征基因的候选基因子集(Feature Gene Candidate Subset, FGCS)。接着，利用粒子群算法的思路，优化其算法过程，设计迭代过程中参数的自适应调整机制，提高其全局最优解的搜索概率和速度。运用优化后的粒子群算法对候选基因进行优选，得到核心信息基因子集(Core Feature Gene Subset, CFGS)，使得该子集尽可能将特征基因包含进来，且减少冗余度，便于后续分类。最后基于CFGS运用分类器进行样本的肿瘤/正常组织分类。这一方法既利用了过滤法的简便特征，又考虑了多变量关系，还利用了粒子群算法的群体智能优势，提高了参数的自适应性，获得了比前述多种方法更为准确、高效的分类结果，能为医学研究和实验提供更为准确和简便的计算方法，可作为医学实验设计参考和仿真演化模型参考。

2　互信息最值过滤法获得候选特征基因子集

如前所述，过滤法采用某种指标对所有基因计算其属于特征基因的权重(该权重反映了各个基因对分类的重要程度或相关程度)，删除权重小于给定阈值的低相关度基因，保留权重较大的前Nt个基因(认为这些基因是与肿瘤密切相关的基因)。常用的权重指标有信噪比(Signal-to-Noise Ratio， SNR)、t-检验(t-statistic)、卡方统计值(Chi-Square)、信息增益(Information Gain， IG)等。权重过滤不依赖于具体的分类算法，可避免过拟合现象，算法实现简单，时间耗费小，能够快速排除大量无关基因和噪声数据；但是，过滤法往往只考虑了单一指标的权重，没有考虑基因之间的关系。实验表明，常存在若干个关系密切的基因的组合作为肿瘤标志的情况，某个权重较大的基因被选中，与它密切相关的其他基因也应当作为信息基因被选中[14]。

互信息(Mutual Information, MI)是信息论里一种信息度量，是一个随机变量中包含的关于另一个随机变量的信息量，可以表示两个随机变量间的统计相关性或者依赖程度。文献[19]提出了一种基于互信息的特征基因快速选取方法，文献[20]提出了利用邻域互信息最大化原则筛选特征基因的方法，它们都利用了同一分类系统的基因在统计学上是高度相关的原理。本文借鉴该思路提出互信息最值过滤原则(Mutual Information Maximum Value Filter Criteria， MIMVFC)，通过在指标权重最大的Nt个基因中进一步寻找相似度(相关性)最大的基因来生成候选特征基因子集。

在信息论中，互信息用熵来计算。熵表示的是不确定性的量度[15]。设离散随机变量x(x∈T1)的概率密度分布函数为p(x)，则x的特征熵H(X)定义为：

(1)

设离散随机变量y(y∈T2)的概率密度分布函数为p(y)，则y的特征熵H(Y)定义为：

(2)

由于熵的值常用于相对运算中，所以式(2)中log定义与底无关，计算时由程序语言中的DLL设置，常设置为以e为底。根据熵的连锁规则，有：

H(x,y)=H(x)+H(y|x)=H(y)+H(x|y)

(3)

定义x和y的互信息I(x,y)：

I(x,y)=H(x)-H(x|y)=H(y)-H(y|x)

(4)

按照熵的定义展开得到：

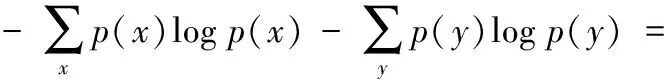
(5)

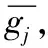
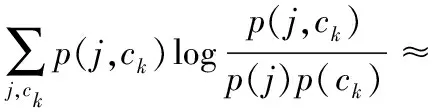
(6)

其中：I(j,ck)的值介于0和1之间，值越小，表示基因j的表达与分类的关系越小，该基因越有可能是管家基因；反之，该基因越有可能提示分类信息，成为候选基因。

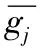
(7)

其中：I(j,k)的值介于0和1之间，值越小，表示基因j和k的表达与分类的关系越小，它们在分类方面的趋近于独立；反之，这两个基因越有可能联合提示分类信息，同时属于候选基因集合。

在选择出了Nt个基因-类别熵最大的基因后，依据互信息最大化原则在剩余的基因中进行选择：按照Max{I(j,k)}即基因-基因熵最大原则，选择与这Nt个基因相关度最高的γNt(γ>0)个基因组成候选特征基因子集。本文的互信息最值过滤原则(MIMVFC)与文献[20]的邻域互信息计算方式不同，本文采用医学实验中基因高低表达个数与总基因个数之间的比例关系作为衡量准则，取代后者较为复杂的对数计算，运算时间明显减少。在结果精度方面虽略有降低，但多次预处理的结果显示该损失可以忽略。

采用MIMVFC能够很快地排除大部分的噪声和管家基因，但得到的候选子集还不是最优、最精简的特征基因子集，需要进一步优化。

3　粒子群优化算法获得特征基因子集

粒子群优化算法源于对鸟群捕食行为的研究，它利用群体中的个体对信息的共享，使得整个群体的运动在问题求解空间中从无序到有序演化，从而获得问题的最优解。PSO的进化公式基于粒子前一时刻的信息，通过处理粒子自身经验信息和群体共享信息决定粒子当前时刻的位置。将特征基因选择问题映射为PSO问题的直观描述是：一群基因试图寻找自己的指示归类，开始时所有基因都不知道自己能够指示哪个类别(或不能指示任何类别)，但是它们知道自己当前的值的表达状态(高或低)，那么求解自己的归属类的最佳策略就是根据适应度函数(Fitness Function)的大小来判断和搜寻目前距离目标最近的基因，从而改变自己的归属，最后得到自己的归属。在PSO中，每个优化问题的解相当于搜索空间中的一个粒子，每个粒子都具有一个位置向量(粒子在解空间的位置)和速度向量(决定下次变化的方向和速度)，并可以根据目标函数来计算当前的所在位置的适应值(fitness value)。在每次的迭代中，种群中的粒子除了根据自身的经验(个体历史位置)进行学习以外，还可以根据种群中最优粒子的经验(社会信息)来学习，从而确定下一次迭代时需要如何调整和改变自己移动的方向和速度。逐步迭代，最终整个种群的粒子趋于最优解。

令Xi=(xi1,xi2,…,xin)代表粒子i的位置向量，Vi=(vi1,vi2,…,vin)代表粒子i的速度向量，其中n为粒子个数即解的个数。经典粒子群优化算法的迭代算子形式如下：

速度向量迭代公式为：

Vi=Vi+δ1r1(Pbesti-Xi)+δ2r2(Gbesti-Xi)

(8)

位置向量迭代公式为：

Xi=Xi+Vi

(9)

其中：Pbesti和Gbesti分别代表粒子i的历史最佳位置向量和全局(种群)历史最佳位置向量；参数δ1和δ2是学习因子，分别表示粒子跟踪自己的历史记录和群体的历史记录的权值；r1和r2为[0,1]区间的随机值，以增加搜索的随机性。种群中的粒子通过不断地向自身和种群的历史信息进行学习，从而可以找出问题的最优解。

但是，实验表明，式(9)中Vi的更新较快，使得PSO算法的全局快搜能力很强，但是局部细搜能力较差。实际上，在算法迭代初期PSO应当有着较强的全局扫描能力，而在算法后期应该具有更强的局部搜索能力。为了达到这一点，文献[11]引入惯性权重，设计了PSO的惯性权重模型：

Vi=ωVi+δ1r1(Pbesti-Xi)+δ2r2(Gbesti-Xi)

(10)

其中：参数ω∈[0，1]是PSO的惯性权重(Inertia Weight)，它的取值位于[0,1]区间。开始令ω取较大值，使得PSO搜索空间大，速度变化快，全局优化能力较强；随着迭代的深入，ω递减，使得PSO在较为确定的小空间内放慢速度搜索；当迭代结束时，ω=0。

上述方法中，ω的值需要人工干预，修改的时机和值主要取决于经验，往往存在较大误差和运气成分。为了自适应修改ω值，更好地模拟粒子的智能运动，本文设计了ω的非线性递减公式：

ω(t+1)=ω(t)×(MaxIter-Iter(t))/MaxIter

(11)

其中：MaxIter为最大迭代次数；Iter(t)为当前已经执行了的迭代次数。这样，在搜索前期，速度降低的速率较大，而搜索后期的速度降低得较慢，并且，速率变化率(加速度)是非线性的。这些都更为符合复杂群体运动系统的特点。

定义粒子的适应度函数来判断粒子目前的位置状况：

fit(Xi)=wA(Xi)+(1-w)(N-R(Xi))/N

(12)

其中：A(Xi)∈[0,1]为使用Xi进行留一交叉验证分类准确度；R(Xi)是Xi中的基因个数；N为每个样本中的基因总数；w∈(0,1)为调节系数。文献[20]对PSO算法的优化主要体现在适应度函数的新设计上，再次利用属性之间的邻域互信息度量适应度；而文本对PSO的优化则体现在运用自调整的非线性递减的惯性权重来自适应调节不同阶段PSO的搜索速度，在适应度函数的设计上未采用互信息而是采用以上一次的适应度作为本次更新的基准，主要原因是经过MIMVFC的过滤，所保留下来的基因都具有较多的高表达属性，互信息的区分能力已经没有第一阶段明显，所以不再采用互信息作为适应度函数的计算因素。

本文提出的惯性权重粒子群优化(Inertia Weight Particle Swarm Optimization, IWPSO)算法框架如图1所示。

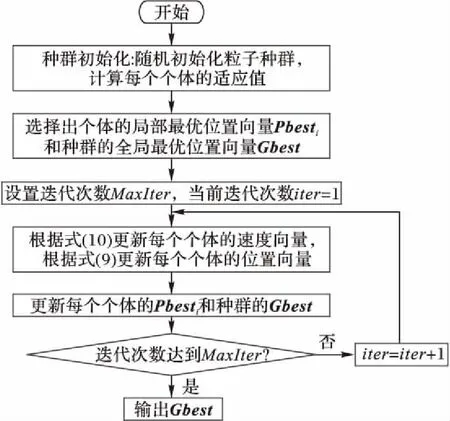
图1　IWPSO算法框架Fig. 1　Framework of IWPSO algorithm

4　实验结果与分析

本文实验环境如下：Windows 7操作系统，Matlab 7编程平台，机器配置CPU Core i3, 3.2 GHz，4 GB内存。

4.1　实验数据集

采用以下三组数据集作为实验数据。1)白血病数据集leukemia(http://www.broad.mit.edu/cgi-bin/cancer/datasets.cgi)，共包含72个样本，7 129个基因,其中：47个样本为急性淋巴白血病(ALL),25个样本为急性骨髓白血病(AML)。2)大肠癌数据集colon 1(http://microarray.princefon.edn/oncology/affydafa/index.htm/)，共包含62个样本，2 000个基因，其中：42个为大肠癌样本，20个为正常组织样本。3)乳腺癌数据集breast cancer(http://mgm.duke.edu/geneme/dnamicro/work/)，共包含49个样本，7 219个基因，其中：24个样本为乳腺癌，25个是正常组织。各基因数据集中的缺失数据已经按照医学实验中的常规线性填充法处理。

4.2　过滤法对特征基因提取的分类结果对比

首先比较本文的互信息最值过滤法MIMVFC、信噪比、t-检验、卡方统计值和信息增益所获得候选特征基因子集进行分类的准确度，分类结果金标准为公开的肿瘤基因表达谱的已经分类的实验数据。比例系数α=β∈[1.5,2]，γ=2，这三个比例系数均来自于大量实验测定所得到的经验值设置，如果α、β过大，γ过小会遗漏部分特征基因,反之则会导致运行代价过大。为保持验证的同一性，所有过滤法得到的候选基因个数Nt均设置为基因总数的1/40(取整)，例如在leukemia和breast cancer数据集中设置为200，在colon 1数据集中设置为50。

将三个肿瘤表达谱数据集分别按1∶1、2∶1、3∶1的比例随机分为训练集和测试集。对于训练集，采用5-折交叉检验法(five-fold cross validation)，将训练集的样本分为5等份，轮流将其中4份样本作为训练样本，剩余1份样本作为测试样本，重复测试直至训练集内所有样本都经过一次测试，得到各个过滤法的最优参数设置。用该配置对于测试集的每个样本进行逐一分类测试。当训练集和测试集为1∶1、2∶1、3∶1时，正确和错误分类样本个数如表1所示。从三个肿瘤基因表达谱库在多个不同训练集：测试集比例下的分类结果可以看到，本文的MIMVFC方法充分考虑了多变量关系，处理结果的准确率在大部分情况下都是最高的，Chi-Square方法次之，优于其他三种单因素过滤法。MIMVFC方法的基因-基因与基因-类别之间的互信息相关原则的有效性得以体现。

分类准确率对比如图2所示。从图2可以看到，MIMVFC在大部分情况下能够获得比其他过滤方法更好的候选特征基因子集，主要原因是原始数据中含有较多的噪声，SNR和IG方法容易受到噪声干扰；而t-statistic和Chi-Square的公式中都采用了标准误差的做法，能够减少噪声的影响，但t-statistic只考虑了单一指标的权重，没有考虑基因之间的关系，所选择的候选特征基因的分类效果不如本文的MIMVFC；Chi-Square准确率较高的原因主要是该方法属于非参数检验，涉及到两个及两个以上样本率(构成比)以及两个分类变量的关联性分析，而非单纯的单因素分析，少数情况下Chi-Square的处理结果更好，这与实际数据的取值范围和分布、数据缺失的填充方法等有一定关系。对同一数据集，不同的训练集∶测试集的比例下五种算法的分类准确率分布如图3所示，其中横坐标为采用的方法编号，1表示SNR,2表示t-statistic,3表示Chi-Square,4表示IG，5表示MIMVFC。由图3可以得知，对同一数据集，当训练集∶测试集的比例增大时，五种过滤法的分类准确率大都呈现提高的趋势，而且在不同比例条件下，MIMVFC的分类准确率比较稳定，浮动范围较小；Chi-Square的准确率接近MIMVFC，但它的结果的偏差范围较大；其他三种过滤方法的准确率较低。同时也可以看到，虽然MIMVFC的分类结果比几种主流的过滤法有较大改善，但是它的总体准确率在83%～89%，还有改进的空间，所以接着借助IWPSO算法进一步提高。

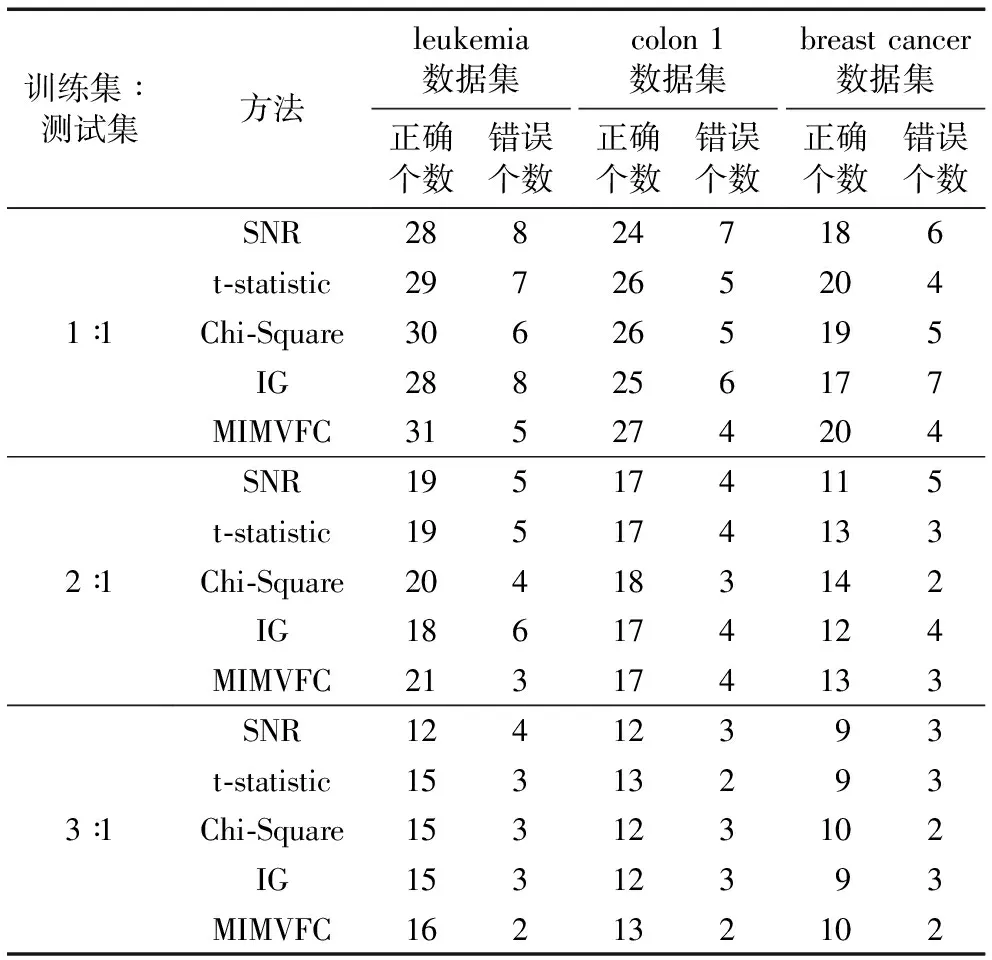
表1　不同训练集与测试集的比例时分类结果Tab. 1　Classification results under different ratio of training samples and test samples

4.3　不同粒子群算法提取特征基因的分类结果对比

对于前述MIMVFC获得的3个肿瘤基因表达谱库的FGCS，分别采用标准PSO、文献[18]的BPSO-CGA和本文IWPSO进行样本的肿瘤/正常组织分类实验，其中标准PSO是改进算法常用的对照算法，而文献[18]的BPSO-CGA则是在肿瘤基因表达谱上分类性能较好的PSO算法，具有可比性。实验指标包括三种方法的特征基因提取规模、分类准确率与运算耗时。

实验参数设置：三种PSO算法的公共参数最大迭代次数MaxIter=1 000，初始粒子个数n=100。标准PSO的参数δ1和δ2初始值根据经验均设置为2，表示粒子跟踪自己的历史记录和群体的历史记录的权值相等；r1和r2为[0,1]区间的随机值，以增加搜索的随机性。文献[18]的BPSO-CGA的初始参数按原文设置。本文IWPSO在标准PSO的基础上，对新增参数初始设置为：惯性权重ω初始值取1，以使得算法初期全局搜索速度快，该值将在迭代过程中由式(11)计算产生动态变化。调节系数w=0.5表示对上一次迭代的结果取50%的置信度，既不过度依赖、也不完全放弃上一次的结果。IWPSO的参数在运行过程中自动迭代更新，无需人工干涉。初始粒子群均采用MIMVFC过滤后的结果FGCS，以相同的起点比较三种PSO算法的有效性。对于每个FGCS各运行10次，从最后得到的特征基因子集大小、耗时和测试集分类准确率三个方面取平均值，综合测试三种粒子群算法的结果(平均值±偏差)如表2所示。

从表2可知，三种PSO算法所获得的特征基因子集中的基因个数都小于预定的初始值100，比候选特征子集的规模小得多，本文IWPSO算法在3个数据集上所获得的特征子集都是最小的，说明它能够有效地提取最精简的基因作为分类代表。IWPSO耗时比标准PSO短，略高于文献[11]的BPSO-CGA，该耗时在实际应用中可以为用户接受。在分类准确率方面，IWPSO是最高的，其次是文献[18]的BPSO-CGA，均高于标准PSO，并且比仅使用MIMVFC过滤法进行分类的准确率有明显提高，说明了本文改进方法的有效性。与文献[20]给出的在相同数据集leukemia dataset上所处理的结果相比，本文的分类精度虽然略低(平均值约低1.96个百分点)，但偏差范围明显较小，说明本文改进方法的稳定性和适应性更好。主要原因是通过对过滤法的改进，利用互信息最值筛选原则获得较高质量的起点，再通过优化的粒子群算法IWPSO，不仅在初始阶段提高了搜索速度，而且在后期最优解可能存在的较小的特定区域进行慢速细致搜索，从而能更好地获得最优解，提升分类准确率。

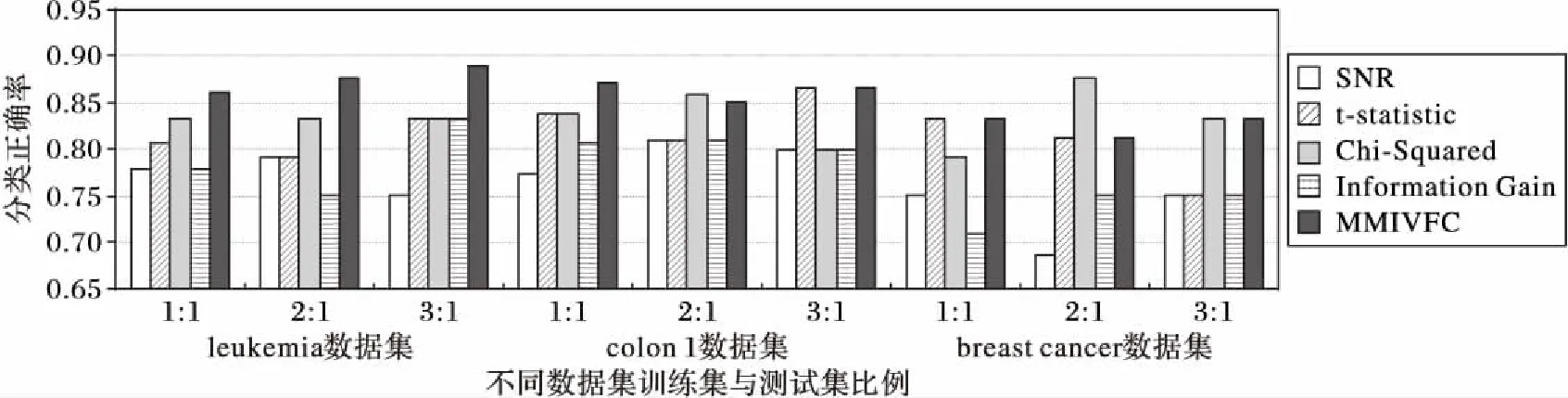
图2　在不同的训练集与测试集比例下五种过滤算法的分类准确率对比Fig. 2　Classification accuracy comparison with different ratio between training samples and testing samples by 5 filter algorithms

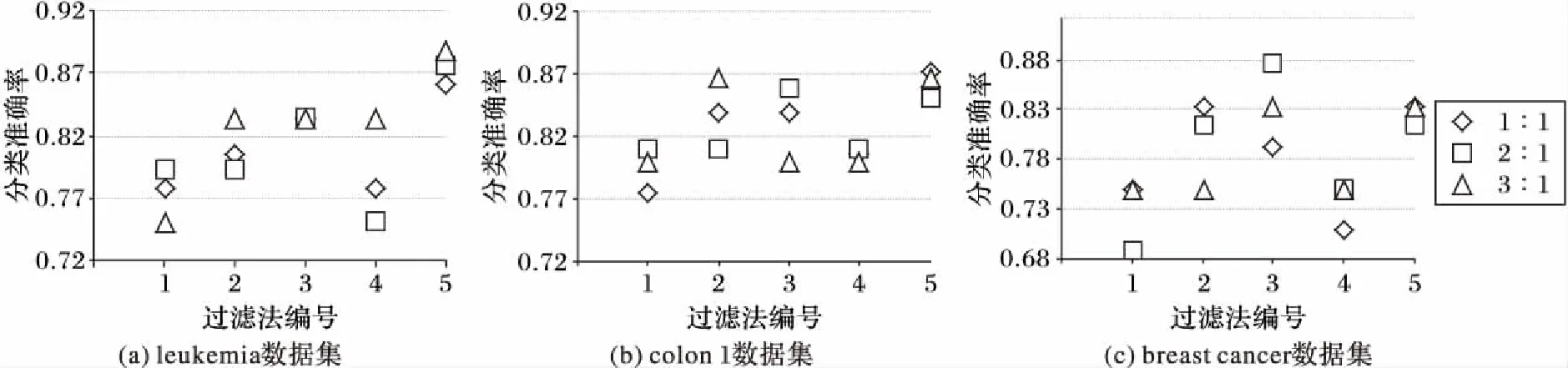
图3　对同一数据集不同的训练集与测试集的比例下五种过滤算法的分类准确率对比Fig. 3　Classification accuracy comparison of 5 filter algorithms with different ratio between training samples and testing samples on same dataset

表2　三种粒子群算法的结果Tab. 2　Comprehensive testing results of three particle swarm optimization algorithms

5　结语

本文设计了基于互信息的最值过滤原则消除与肿瘤分类无关的噪声和冗余基因，这种思路不仅容易实现、计算简便，而且由于考虑了基因-基因与基因-类别的互信息，更符合基因优选原理，所获得的候选基因子集更为准确且规模更小，不仅可以减轻后续分类器的计算负担，还可以提高分类器的分类准确度，便于分子生物学实验设计和验证，对于肿瘤标志物的查找和肿瘤发生发展分子机制的阐明具有一定的提示意义。

本文还通过对PSO算法加以惯性权重调控，使得迭代过程中的权值随着搜索阶段而自适应改变，实现了初期快速搜索、后期准确定位。过滤法与粒子群优化算法的结合运用，不仅提高了结果的准确度，而且大幅度减少了运算时间，对于海量数据的分析和处理提供了很好的探索方向。

本文方法目前仅用于二分类问题，如果要用于多分类问题，需要进一步探索多个类别之间参数阈值的设置方法，这是正在与医学专业人员讨论的问题，也是今后的突破点之一。下一步的工作包括：将探索区域扩展到肿瘤亚型的自动分类方面，即多分类问题的求解；沿着基因-基因熵的思路，探索寻找指定属性的基因的通用方法；对PSO算法根据不同的具体问题的要求实现对应参数的自适应策略。

参考文献(References)

[1]HSIEH S Y, CHOU Y C. A faster cDNA microarray gene expression data classifier for diagnosing diseases [J]. IEEE//ACM Transactions on Computational Biology & Bioinformatics, 2016, 13 (1): 43-54.

[2]BUTT H Z, SYLVIUS N, SALEM M K, et al. Microarray-based gene expression profiling of abdominal aortic aneurysm [J]. European Journal of Vascular and Endovascular Surgery, 2016, 52(1): 47-55.

[3]徐久成，李涛，孙林，等.基于信噪比与邻域粗糙集的特征基因选择方法[J].数据采集与处理,2015,30(5):973-981. (XU J C, LI T, SUN L, et al. Feature gene selection based on SNR and neighborhood rough set [J]. Journal of Data Acquisition and Processing, 2015, 30(5): 973-981.)

[4]ZHAO Z, WANG L, LIU H. Efficient spectral feature selection with minimum redundancy [C]// Proceedings of the 2010 Twenty-Fourth AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2010: 673-678.

[5]李晓波,彭司华.多类别肿瘤分类的特恒基因选择方法研究[J].复旦学报,2014,53(3):305-312. (LI X B, PENG S H. Informative gene selection methods for multi-category cancer classification [J]. Journal of Fudan University (Natural Science), 2014, 53(3): 305-312.)

[6]徐久成,冯森,穆辉宇.基于信噪比与随机森林的肿瘤特征基因选择[J].河南师范大学学报(自然科学版),2017,45(2):87-92. (XU J C, FENG S, MU H Y. Tumor feature gene selection based on SNR and random forest [J]. Journal of Henan Normal University (Natural Science Edition), 2017, 45(2): 87-92.)

[7]YU B, LI S, LIU H J. A hybrid gene selection method for tumor classification based on genetic algorithm and support vector machine [J]. Journal of Computational and Theoretical Nanoscience, 2015, 12(11): 4730-4735.

[8]HU Q H, AN S, YU D R. Soft fuzzy rough sets for robust feature evaluation and selection [J]. Information Sciences, 2010, 180(22): 4384-4400.

[9]CHEN D G, ZHAO S Y. Local reduction of decision system with fuzzy rough sets [J]. Fuzzy Sets and Systems, 2010, 161(13): 1871-1883.

[10]陈涛,洪增林,邓方安.基于优化的邻域粗糙集的混合基因选择算法[J].计算机科学,2014,41(10):291-294. (CHEN T, HONG Z L, DENG F A. Hybrid gene selection algorithm based on optimized neighborhood rough set [J]. Computer Science, 2014, 41(10): 291-294.)

[11]LI X, PENG S, CHEN J, et al. SVM-T-RFE: a novel gene selection algorithm for identifying metastasis-related genes in colorectal cancer using gene expression profiles [J]. Biochemical and Biophysical Research Communications, 2012, 419(2): 148-153.

[12]MAULIK U, MUKHOPADHYAY A, CHAKRABORTY D. Gene-expression-based cancer subtypes prediction through feature selection and transductive SVM [J]. IEEE Transactions on Biomedical Engineering, 2013, 60(4): 1111-1117.

[13]谢志伟,王志明,骆剑锋.基于RD-SVM的肿瘤信息基因选择算法[J].计算机应用与软件,2015,32(5):310-313. (XIE Z W, WANG Z M, LUO J F. Tumor informative gene selection algorithm based on RD-SVM [J]. Computer Applications and Software, 2015, 32(5): 310-313.)

[14]KANEHISA M, GOTO S, SATO Y, et al. Data, information, knowledge and principle: back to metabolism in KEGG [J]. Nucleic Acids Research, 2014, 42: D199-D205.

[15]杨淑莹.群体智能与仿生计算[M].北京:电子工业出版社，2016:109-124. (YANG S Y. Swarm Intelligence and Bionic Computation [M]. Beijing: Publishing House of Electronics Industry, 2016: 109-124.)

[16]ZHAN Z H, ZHANG J, LI Y, et al. Adaptive particle swarm optimization [J]. IEEE Transactions on Systems, Man, and Cybernetics — Part B: Cybernetics, 2009, 39(6): 1362-1381.

[17]陈伟,周頔,孙俊,等.一种采用完全学习策略的量子行为粒子群优化算法[J].控制与决策,2012,27(5):719-730. (CHEN W, ZHOU D, SUN J, et al. Improved quantum-behaved particle swarm optimization algorithm based on comprehensive learning strategy [J]. Control and Decision, 2012, 27(5): 719-730.)

[18]CHUANG L Y, YANG C H, LI J C, et al. A hybrid BPSO-CGA approach for gene selection and classification of microarray data [J]. Journal of Computional Biology, 2012, 19(1): 68-82.

[19]XU J C，XU T H，SUN L，et al. An efficient gene selection technique based on fuzzy C-means and neighborhood rough set [J]. Applied Mathematics & Information Sciences, 2014, 8(6): 3101-3110.

[20]徐天贺,马媛媛,徐久成.一种基于邻域互信息最大化和粒子群优化的特征基因选择方法[J].小型微型计算机系统,2016,37(8):1775-1779. (XU T H, MA Y Y, XU J C. Efficient gene selection technique based on maximum neighborhood mutual information and particle swarm optimization [J]. Journal of Chinese Computer Systems, 2016, 37(8): 1775-1779.)