可变直觉模糊多粒度粗糙集模型及其近似分布约简算法

万志超，宋　杰，沈永良

(1.计算智能与信号处理教育部重点实验室(安徽大学)，合肥 230601；　2.安徽大学 计算机科学与技术学院，合肥 230601)(*通信作者电子邮箱luckwan12@163.com)

0　引言

粗糙集理论是Pawlak教授[1]于1982年提出的一种处理不确定性知识的数据分析理论，它的基本思想是通过等价关系将知识论域划分成知识粒，然后对目标概念进行近似逼近。由于该理论的自身特性，目前已广泛运用于机器学习、智能信息处理和数据挖掘等领域[2-4]。

近年来，随着研究的深入，传统的粗糙集理论也暴露了一些局限性，因此研究人员对粗糙集模型也作了大量的推广，例如，Ziarko[5]提出了变精度粗糙集，使得粗糙集模型降低了对噪声数据的敏感度;Duboid等[6]提出了模糊粗糙集;张植明等[7]提出了基于直觉模糊覆盖的直觉模型粗糙集;Lin[8]提出了邻域粗糙集模型。这些模型不断地被提出，使得粗糙集理论逐渐趋于完善。最近，Qian等[9-10]在粒计算的视角下提出了多粒度粗糙集模型，该模型通过多个等价关系对论域进行划分，进而构造出了多重的知识粒对目标对象进行近似逼近，这样可以对目标概念进行更为全面的知识挖掘[9]。目前该模型已成为粗糙集理论的研究热点[10-12]。

直觉模糊粗糙集[7]是粗糙集理论的一种常见模型，由于该模型以直觉模糊集[13]作为理论基础，通过隶属度、非隶属度和犹豫度三个视角来刻画对象的隶属关系，有着更好的数据相似性度量效果[13]，这使得直觉模糊粗糙集有着更优越的近似逼近刻画，目前受到了学者们的广泛关注[7,14-16]。

虽然多粒度粗糙集和直觉模糊粗糙集都是粗糙集理论中两种优秀的模型，但是很少有学者考虑将它们进行结合，因此本文在前人研究的基础上，提出了一种直觉模糊多粒度粗糙集模型，并定义了乐观和悲观的两种形式。近年来由于张明等[12]提出了多粒度粗糙集模型中近似集定义的不合理情况，并给出了一种改进的模型，本文采用该改进方法，进一步地提出了改进的可变直觉模糊多粒度粗糙集模型，并证明了相关的性质。实例分析表明，所提出的可变直觉模糊多粒度粗糙集模型改善了原先模型对于近似集定义过于宽松和过于严格的情形，在近似逼近方面更具合理性。属性约简是粗糙集模型中一种重要的应用[17-18]，在所提出的可变直觉模糊多粒度粗糙集模型基础上，本文进一步地给出了该模型的近似分布约简算法，UCI实验结果也验证了该算法具有更好的约简性能。

1　相关概念

1.1　直觉模糊粗糙集

直觉模糊集是Atanassov[13]在模糊集理论上的拓展，它通过隶属度、非隶属度和犹豫度这三个方面来描述信息的不确定性，相比模糊集更具灵活性。

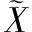
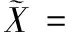
(1)

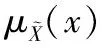
定义2对于一个全集U，定义U上的直觉模糊关系Ω为:

Ω={〈(x,y),μΩ(x,y),νΩ(x,y)〉|(x,y)∈U×U}

(2)

其中:μΩ∈[0,1],νΩ∈[0,1],并且满足μΩ+νΩ∈[0,1]。U上的直觉模糊关系Ω可用关系矩阵表示为:

(3)

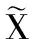
(4)

(5)

其中:

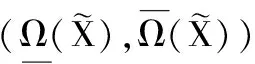
1.2　多粒度粗糙集

多粒度粗糙集模型是Qian等[9]在传统粗糙集理论上的推广，该模型通过多个等价关系方式对近似对象进行粗糙逼近，从而对研究对象达到更为全面的认识。

定义4设信息系统IS=(U,AT),其中：U为非空有限对象集，被称为全集；AT为全体属性集。{A1,A2,…,Am}为AT上m个属性子集，∀X⊆U关于这m个属性子集的乐观多粒度粗糙集的下近似和上近似分别定义为：

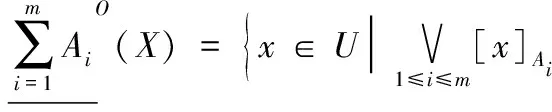
(6)

(7)

其中[x]Ai表示对象x在等价关系Ai下的等价类。

定义5对于信息系统IS=(U,AT),设{A1,A2,…,Am}为AT上m个属性子集，∀X⊆U关于这m个属性子集的悲观多粒度粗糙集的下近似和上近似分别定义为:

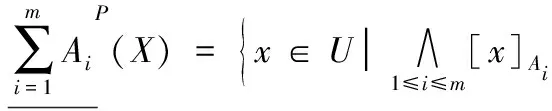
(8)

(9)

2　可变直觉模糊多粒度粗糙集模型

直觉模糊粗糙集[7]和多粒度粗糙集[9]是粗糙集理论中两种重要的模型，直觉模糊粗糙集通过隶属度、非隶属度和犹豫度三个方面对不确定性对象具有更好的近似逼近效果[16]，而多粒度粗糙集通过多视角对目标概念进行分析。为了融合两种模型的优势，本文将两种模型结合，提出基于直觉模糊集的多粒度粗糙集模型。

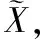
(10)

(11)

其中:

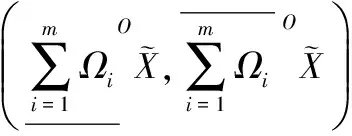
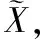
(12)

(13)

其中:

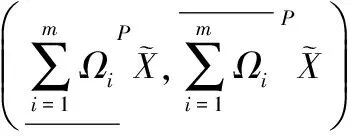
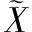
(14)

(15)

证明根据定义3和定义6可直接得到性质1成立。

在劳动力价格日趋高涨的情况下，减少劳动力工作日，减轻劳动强度，提高劳动效益，加快投入装备，实现自动化和机械化、半机械化是重要的途径，针对土墙日光温室，一是配置滴灌设施，实现小规模2-10栋温室规模的水肥一体化设施，实现灌溉浇水、施肥施药等的自动化，降低温室内湿度，减少病虫害。二是对温室通风口和外保温改造，配置温度湿度的监控装置，并同通风口、卷帘机和手机等联结，形成自动化的日光温室植物生长因素监控遥控系统。三是对于比较大的温室，增加角铁轨道或悬挂吊轨输送采摘蔬菜和生产资料。

(16)

(17)

证明根据定义3和定义7可直接得到性质2成立。

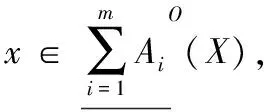
观察性质1和性质2可以发现，所提出的直觉模糊多粒度粗糙集模型中也出现了相同的弊端，为了解决这一问题，本文将张明等[12]提出的可变多粒度粗糙集融入到所提的模型中。

(18)

(19)

这里满足Θ′⊆Θ,|Θ′|/|Θ|=α,并且:

(20)

(21)

这里满足Θ′⊆Θ,|Θ′|/|Θ|≥α,并且:

通过定义8和定义9可以发现，可变直觉模糊多粒度粗糙集模型中的参数α用来限定模型中直觉模糊关系的吸取或合取，这样相比原先的直觉模糊多粒度粗糙集模型具有更好的灵活性。可变直觉模糊多粒度粗糙集模型满足如下性质。

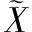
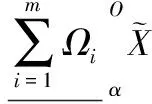
(22)

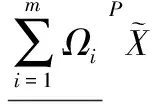
(23)

当α=1时:

(24)

(25)

证明当0<α≤1，即Θ′⊆Θ，那么根据定义8有:

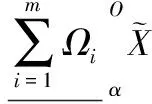
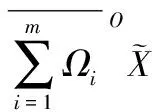
证毕。

在直觉模糊乐观多粒度粗糙集模型中，下近似的定义过于宽松，上近似的定义过于严格，通过性质3的式(22)可以发现，含参数α的可变下近似小于原先的下近似，含参数α的可变上近似大于原先的上近似，说明了含参数的下近似定义较为严格一点，上近似定义较为宽松一点，这样消除了原先直觉模糊乐观多粒度粗糙集模型的缺陷，对近似集具有更合理的拟合效果。同样地，通过性质3的式(23)得出可变直觉模糊悲观多粒度粗糙集模型也达到了更合理的近似逼近效果。

此外，在性质3的式(24)、(25)中，当α=1时，可变直觉模糊多粒度粗糙集模型便退化为直觉模糊多粒度粗糙集模型，因此直觉模糊多粒度粗糙集模型是可变模型的特例，可变模型是直觉模糊多粒度粗糙集模型的泛化。

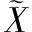
(26)

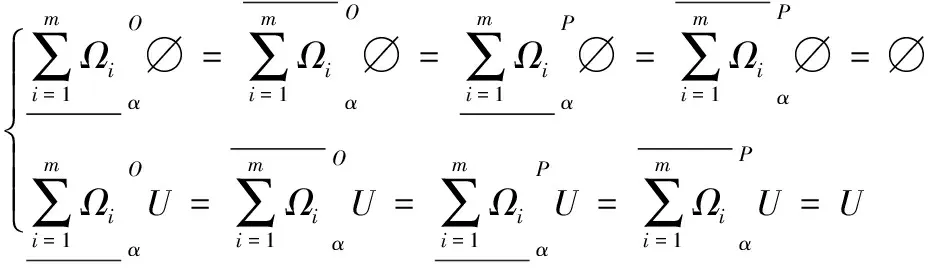
(27)

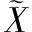
(28)

α1≤α2⟹

(29)

证明根据定义8和定义9，式(26)、(27)显然成立。

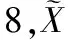
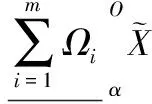
在式(29)中，α1≤α2有Θ1⊆Θ2，那么：

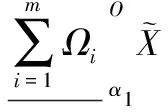
证毕。

在性质4的式(26)～(28)表明，可变直觉模糊多粒度粗糙集模型仍然满足原先模型的一些最基本的性质，但是在式(29)中，设置不同的参数α值，可以得到不同大小的上下近似，这就表明，可以通过设置参数α来调节模型上下近似的宽松和严格程度，这样使得该模型具有较好的灵活性。

3　实例分析

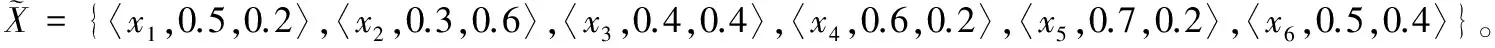
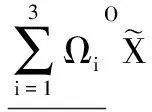
接下来本文设定参数α=2/3，计算出可变直觉模糊乐观多粒度粗糙集以及悲观多粒度粗糙集，其结果为：

观察可以发现：首先近似集结果满足性质3；其次，相对直觉模糊多粒度粗糙集模型，可变模型的粗糙集在宽松和严格方面有了一定的改善，使得可变直觉模糊多粒度粗糙集模型拥有了更合理的近似逼近效果。同时也可以根据实际的需求来适当地选取α值。

4　近似分布约简

属性约简是粗糙集理论在机器学习领域中一种重要的应用[2,17-18]，在多粒度粗糙集模型中，基于近似分布的属性约简是目前研究的重点[9-10,18]。在本章将探究可变直觉模糊多粒度粗糙集模型关于近似分布的属性约简问题。

定义10设决策信息系统DIS=(U,C∪D),其中U为非空有限对象集，C为信息系统的条件属性集，D为决策属性集，且C∩D=∅。决策属性集D诱导出的划分为U/D={D1,D2,…,Dr}。设{A1,A2,…,Am}为C上m个条件属性子集，并且条件属性子集Ai诱导出的直觉模糊关系为ΩAi。令0<α≤1,定义：

(30)

(31)

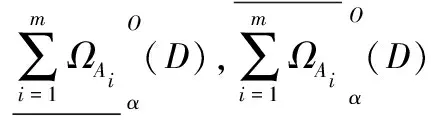
(32)

(33)

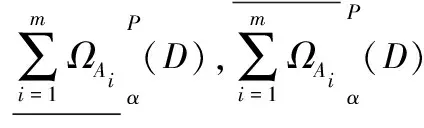
定义11对于决策信息系统DIS=(U,C∪D),决策属性集D诱导出的划分为U/D={D1,D2,…,Dr}。0<α≤1，设{A1,A2,…,Am}为C上m个条件属性子集，诱导出的一组直觉模糊关系为{ΩA1,ΩA2,…,ΩAm}，另外设{B1,B2,…,Bm}也为C上m个条件属性子集，并且满足Bi⊆Ai(1≤i≤m)，诱导出的一组直觉模糊关系为{ΩB1,ΩB2,…,ΩBm}。若{B1,B2,…,Bm}是{A1,A2,…,Am}的乐观下近似分布相对约简当且仅当：

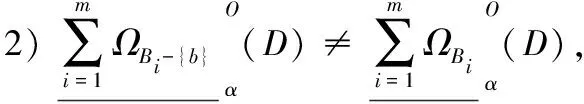
若{B1,B2,…,Bm}是{A1,A2,…,Am}的乐观上近似分布相对约简当且仅当：

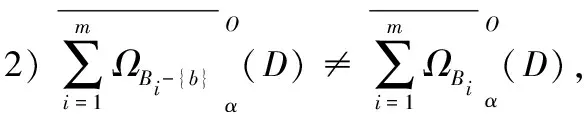
同理，对于决策信息系统DIS=(U,C∪D),决策属性集D诱导出的划分为U/D={D1,D2,…,Dr}。0<α≤1，设{A1,A2,…,Am}为C上m个条件属性子集，诱导出的一组直觉模糊关系为{ΩA1,ΩA2,…,ΩAm}，另外设{B1,B2,…,Bm}也为C上m个条件属性子集，并且满足Bi⊆Ai(1≤i≤m)，诱导出的一组直觉模糊关系为{ΩB1,ΩB2,…,ΩBm}。若{B1,B2,…,Bm}是{A1,A2,…,Am}的悲观下近似分布相对约简当且仅当：

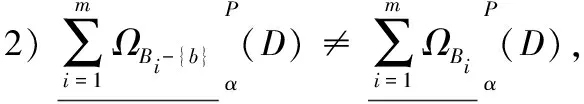
若{B1,B2,…,Bm}是{A1,A2,…,Am}的悲观上近似分布相对约简当且仅当：

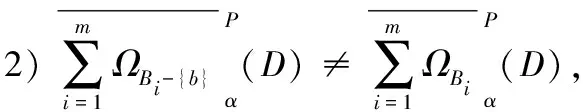
在定义11中关于可变直觉模糊多粒度粗糙集模型的近似分布约简中，条件(1)表示的是乐观/悲观近似分布约简集和原属性子集具有相同的近似分布，即具备相同的分类性能，条件(2)保证乐观/悲观近似分布约简集的极小性。同时，如果{B1,B2,…,Bm}既是乐观/悲观下近似分布约简又是乐观/悲观上近似分布约简，那么称{B1,B2,…,Bm}是{A1,A2,…,Am}的乐观/悲观近似分布约简。

根据定义11，可以得到基于可变直觉模糊多粒度粗糙集模型的属性重要度定义。

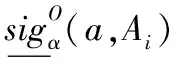
(34)

(35)

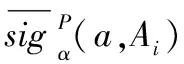
(36)

(37)

另外，这里定义空集诱导出的直觉模糊关系为Ω∅={〈(x,y),0,1〉|(x,y)∈U×U}。

在定义12中，如果a∈Ai关于Ai的属性重要度的值为0，说明{A1,A2,…,Ai-{a},…,Am}和{A1,A2,…,Ai,…,Am}的在可变直觉模糊多粒度粗糙集下的近似分布是一致的，也就是说a关于Ai是冗余的，因此需要把属性a在Ai中进行删除。根据定义12，接下来给出可变直觉模糊多粒度粗糙集下的近似分布约简算法。

算法1乐观下近似分布约简。

输入决策信息系统DIS=(U,C∪D)，参数α，m个属性子集{A1,A2,…,Am};

输出下近似分布约简{B1,B2,…,Bm}。

步骤1初始化Bi=∅(1≤i≤m)。

步骤2计算决策属性划分U/D。

步骤3对于{A1,A2,…,Ai,…,Am}中每个属性子集Ai,依次进行步骤4～5计算。

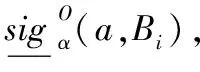
若出现多个满足条件的属性，任选其中一个。

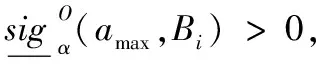
步骤6返回{B1,B2,…,Bm}。

类似于算法1，还可以得到决策信息系统的乐观上近似分布约简，以及悲观下/上近似分布约简。

5　实验分析

为了验证本文所提出的可变直觉模糊多粒度粗糙集模型的优势，利用本文所提出的近似分布约简算法和其他多粒度粗糙集模型的近似分布约简算法分别对相同的数据集进行约简，最后对分布约简的大小和分布约简的分类性能进行比较。参与实验的数据集如表1所示，这些数据集均来自于UCI机器学习数据集库。

实验中选取的对比算法分别为:1)模糊多粒度决策理论粗糙集模型的近似分布约简算法[19](记为算法A1和算法A2);2)多粒度双量化决策理论粗糙集的近似分布约简算法[20](记为算法B1和算法B2);3)可变多粒度粗糙集模型的近似分布约简算法[12](记为算法C1和算法C2)。记本文所提出的可变直觉模糊多粒度粗糙集的近似分布约简算法为算法D1和算法D2。上述中标记为1的算法均为乐观下近似分布约简，标记为2的算法均为乐观上近似分布约简。另外，由于本文提出的是直觉模糊关系下的多粒度粗糙集模型，对象之间的直觉模糊关系采用文献[21]提出的构造方法，即通过证据理论中信任函数和似然函数等函数去度量直觉模糊关系中的隶属度和非隶属度。

本实验参与比较的均为各类多粒度粗糙集模型下的近似分布约简算法，在进行实验前需要构造出一组属性子集。表2所示的是表1中6个数据集构造出的属性子集结果，其中属性子集的结果用属性子集的大小来表示，例如对于数据集wine，属性子集的大小结果为{4,4,5}，即对应的3个属性子集分别为{1,2,3,4},{5,6,7,8},{9,10,11,12,13}。同理，其余5个数据集也是用同样的方法来表示。

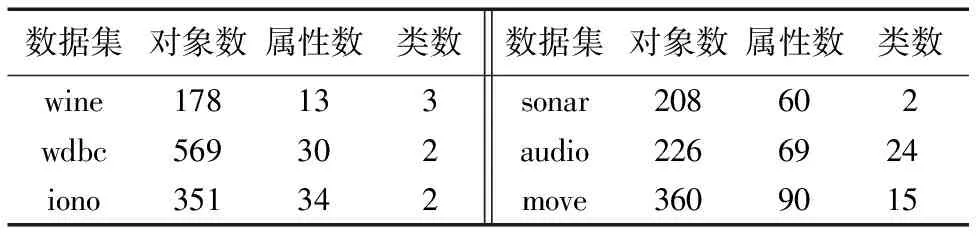
表1　UCI数据集Tab. 1　UCI data sets

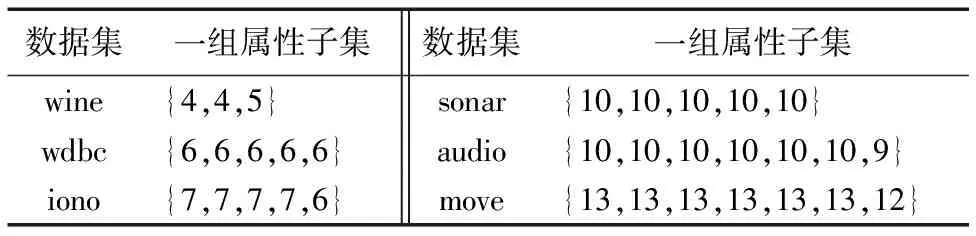
表2　多粒度属性子集结果Tab. 2　Multi-granulation attribute subset results

表3、表4分别是四种下近似分布约简算法和四种上近似分布约简算法对表1各个数据集的属性约简结果比较。其中算法C1、C2、D1和D2均含有参数α，具体的取值在表中的括号里标注。由表3可以很明显地看出，算法A1和算法B1约简出的属性子集包含了更少的属性，这主要是由于算法A1和算法B1是在传统多粒度粗糙集模型的基础上构造出的近似分布约简，对近似目标的下近似粗糙逼近过于宽松，使得约简集中每个属性的属性重要度评估不是特别的合理，约简时剔除了一些比较重要的属性，导致了每个属性子集的约简集比较小。而算法C1和算法D1相比算法A1和算法B1有着较大的约简集，例如数据集wine、sonar、audio和move，这主要是由于算法C1和算法D1都是通过可变参数α的方式限制了多粒度粗糙集模型的近似逼近程度，改善了原先多粒度粗糙集模型中下近似逼近过于宽松的缺陷[12]，对于一些比较重要的属性得到了保留，因此对应的约简集较大。算法D1是基于可变直觉模糊多粒度粗糙集构造的约简算法，直觉模型关系在刻画数据相似性方面具有更高的优越性，因此对属性重要度有着更为精准的度量，从而使得算法D1的约简集小于算法C1的约简集。在表4中则可以观察到相反的结果。算法A1和算法B1对近似目标的上近似粗糙逼近过于严格，导致了每个属性子集的约简集比较大，而算法C1和算法D1通过可变参数α的方式改善了这种上近似逼近过于严格的缺陷，使得算法C1和算法D1得到的约简结果比较小，同时算法D1的约简集更小，例如数据集wine、wdbc、iono和audio等。因此通过近似分布的约简结果可以看出本文所提模型具有一定的优越性。

表3　下近似分布约简结果比较Tab. 3　Comparison of reduction results of lower approximation distribution

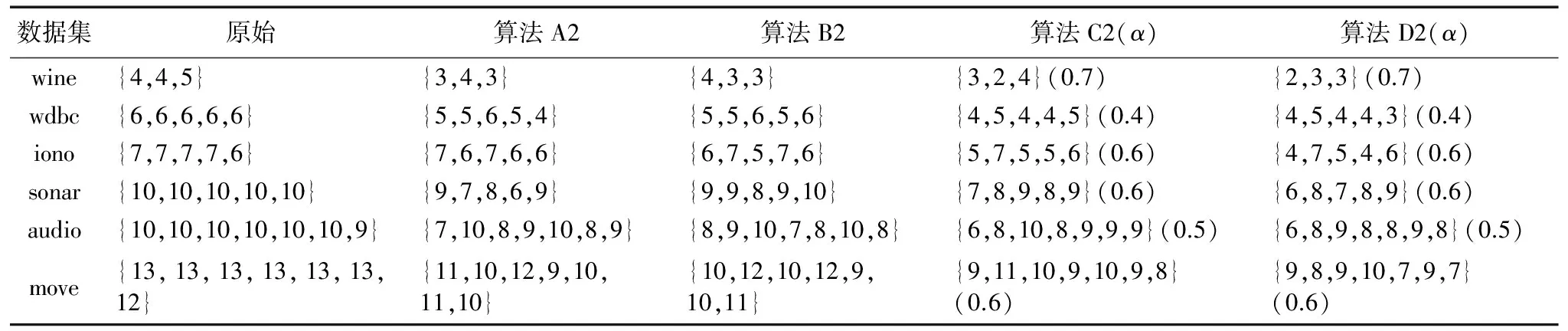
表4　上近似分布约简结果比较Tab. 4　Comparison of reduction results of upper approximation distribution

为了评估四类模型近似分布约简算法的约简结果的有效性，本实验通过粗糙集模型中关于决策属性的近似精度度量来体现[9,12,18]，近似精度反映了粗糙集模型中近似目标的逼近程度。从表5中四种下近似分布约简的近似精度度量结果可以看出，算法A1和A2约简结果的近似精度和算法B1和B2约简结果的近似精度普遍比较高，这主要是由于这两种模型的下近似和上近似采用传统的方法来描述，即下近似的逼近过于宽松，上近似的逼近过于严格，从而导致了近似精度过高，这显然是不合理的。而算法C1和C2约简结果的近似精度和算法D1和D2约简结果的近似精度结果就稍微低一点，这主要是由于这两种模型的参数α的加入能很好地改善原先多粒度粗糙集模型的缺陷，有利于反映出近似目标和属性子集之间真实的近似度量效果，算法D1和D2约简结果的近似精度在部分数据集的值更低一点，这主要是直觉模糊关系对数据相似性的刻画具有更高优越性的结果。从表5中四种上近似分布约简的近似精度度量结果，同样能看出类似的规律。因此通过对于近似精度整体分析，本文所提出的可变直觉模糊多粒度粗糙集模型具有更好的近似逼近效果。

在本文所提出的可变直觉模糊多粒度粗糙集模型中，参数α是一个很重要的参数，它的取值大小直接影响到了近似目标近似逼近效果。为了验证参数α对近似分布约简的影响，接下来将参数α在[0,1]区间上依次取值分别进行实验，表1中各个数据集的下近似分布约简和上近似分布约简的实验结果分别如图1和图2所示。

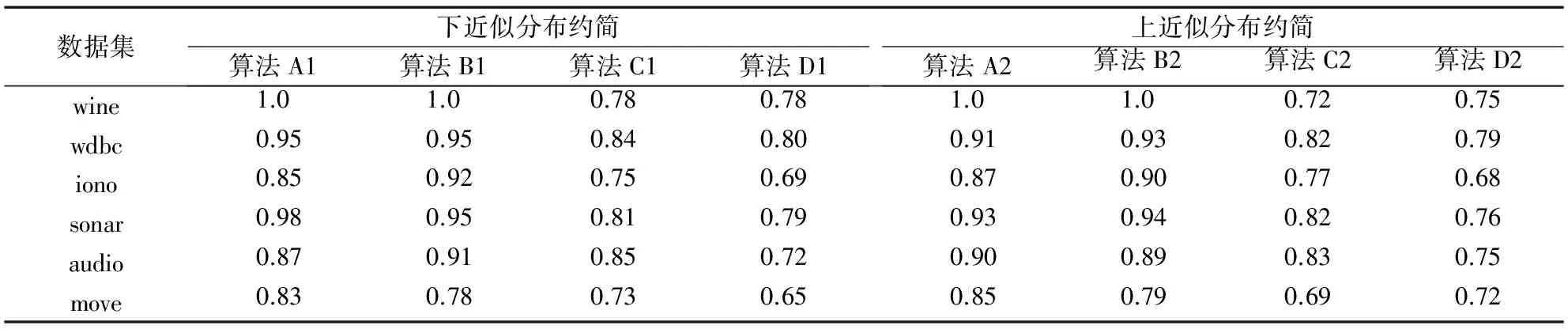
表5　近似分布约简近似精度比较Tab. 5　Comparison of approximation accuracy of approximation distribution reduction

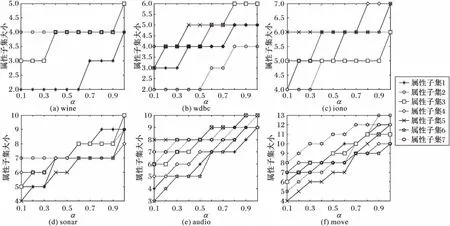
图1　下近似分布约简结果Fig. 1　Reduction results of lower approximation distribution

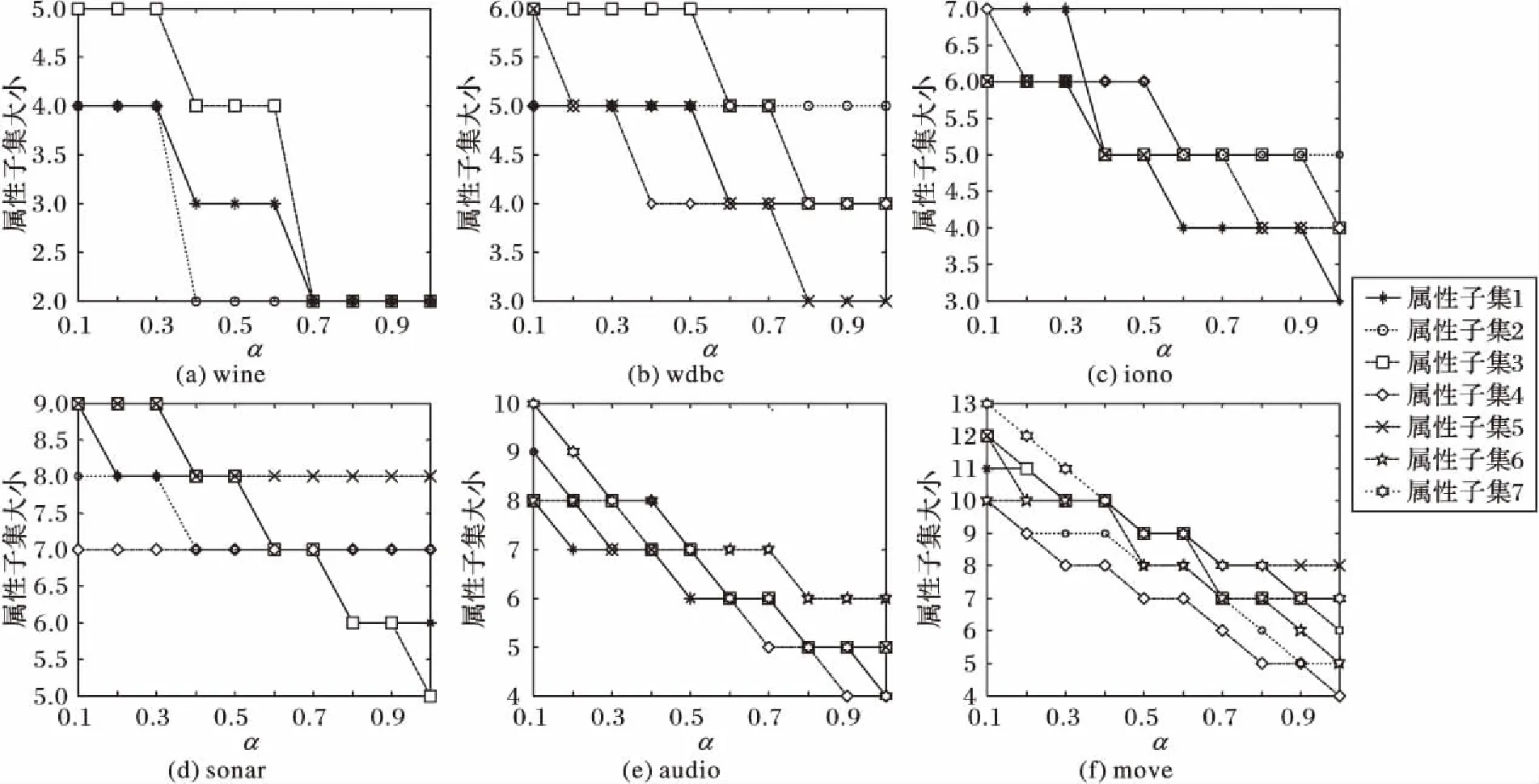
图2　上近似分布约简结果Fig. 2　Reduction results of upper approximation distribution

在图1中，随着参数α的逐渐增加，其下近似分布约简中每个属性子集的大小是逐渐增加的，这主要是由于参数α的值逐渐增大，逐渐增加了乐观下近似定义的严格程度，使得约简的严格程度也相应增加，因此属性子集逐渐增大。在图2中，随着参数α的逐渐增加，上近似分布约简中每个属性子集的大小是逐渐减少的，这主要是由于参数α的值逐渐增大，逐渐减小了上近似定义的严格程度，从而使得约简的严格程度也相应逐渐减小，属性子集的大小逐渐减小。因此综合起来分析可以发现，本文所提出的可变直觉模糊多粒度粗糙集模型在近似逼近和约简方面都更具一定的灵活性，而参数α可以根据实际的需求灵活选取。

6　结语

多粒度粗糙集和直觉模糊粗糙集是粗糙集理论的两种重要的模型，为了融合各自的优点，本文提出直觉模糊多粒度粗糙集，针对该模型对于近似目标的粗糙逼近过于宽松和过于严格的问题作了进一步的改进，提出了可变直觉模糊多粒度粗糙集模型，并通过理论分析和实例验证了该模型的合理性。同时本文进一步地给出了可变直觉模糊多粒度粗糙集模型的近似分布约简算法，在UCI数据集上的实验结果表明，所提出的属性约简算法具有更好的约简性能，同时也验证了本文的可变直觉模糊多粒度粗糙集模型在近似逼近和数据降维方面均具有更高的优越性。接下来，将针对所提出模型的规则提取方法作进一步研究。

参考文献:

[1]PAWLAK Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.

[2]ZHANG X, MEI C, CHEN D, et al. Feature selection in mixed data: a method using a novel fuzzy rough set-based information entropy [J]. Pattern Recognition, 2016, 56: 1-15.

[3]ZENG A, LI T, HU J, et al. Dynamical updating fuzzy rough approximations for hybrid data under the variation of attribute values [J]. Information Sciences, 2016, 378(1): 363-388.

[4]张钧波,李天瑞,潘毅,等.云平台下基于粗糙集的并行增量知识更新算法[J].软件学报,2015,26(5):1064-1078. (ZHANG J B, LI T R, PAN Y, et al. Parallel and incremental algorithm for knowledge update based on rough sets in cloud platform [J]. Journal of Software, 2015, 26(5): 1064-1078.)

[5]ZIARKO W. Variable precision rough set model [J]. Journal of Computer and System Sciences, 1993, 46(1): 39-59.

[6]DUBOID D, PRADE H. Rough fuzzy sets and fuzzy rough sets [J]. International Journal of General Systems, 1990, 17(2/3): 191-209.

[7]张植明,白云超,田景峰.基于覆盖的直觉模糊粗糙集[J].控制与决策，2010,25(9):1369-1373. (ZHANG Z M, BAI Y C, TIAN J F. Intuitionistic fuzzy rough sets based on intuitionistic fuzzy coverings [J]. Control and Decision, 2010, 25(9): 1369-1373.)

[8]LIN T Y. Rough sets, neighborhood systems and approximation [J]. World Journal of Surgery, 1986, 10(2): 189-94.

[9]QIAN Y, LIANG J, YAO Y, et al. MGRS: a multi-granulation rough set [J]. Information Sciences: an International Journal, 2010, 180(6): 949-970.

[10]QIAN Y, LIANG J, DANG C. Incomplete multigranulation rough set [J]. IEEE Transactions on Systems, Man and Cybernetics — Part A: Systems and Humans, 2010, 40(2): 420-431.

[11]谭安辉,李进金,吴伟志.多粒度粗糙集和覆盖粗糙集间的近似与约简关系[J].模式识别与人工智能,2016,29(8):691-697. (TAN A H, LI J J, WU W Z. Approximation and reduction relationships between multi-granulation rough sets and covering rough sets [J]. Pattern Recognition and Artificial Intelligence, 2016, 29(8): 691-697)

[12]张明,唐振民,徐维艳,等.可变多粒度粗糙集模型[J].模式识别与人工智能,2012,25(4):709-720. (ZHANG M, TANG Z M, XU W Y, et al. Variable multigranulation rough set model [J]. Pattern Recognition and Artificial Intelligence, 2012, 25(4): 709-720.)

[13]ATANASSOV K T. Intuitionistic fuzzy sets [J]. Fuzzy Sets & Systems, 1986, 20(1): 87-96.

[14]ZHANG X, CHEN D, TSANG E C C. Generalized dominance rough set models for the dominance intuitionistic fuzzy information systems [J]. Information Sciences, 2017, 378: 1-25.

[15]LIU Y, LIN Y. Intuitionistic fuzzy rough set model based on conflict distance and applications [J]. Expert Systems, 2015, 31: 266-273.

[16]HUANG B, GUO C-X, LI H-X, et al. Hierarchical structures and uncertainty measures for intuitionistic fuzzy approximation space [J]. Information Sciences, 2016, 336: 92-114.

[17]姚晟,徐风，赵鹏，等.基于邻域量化容差关系粗糙集模型的特征选择算法[J].模式识别与人工智能，2017，30(5):416-428. (YAO S, XU F, ZHAO P, et al. Feature selection algorithm based on neighborhood valued tolerance relation rough set model [J]. Pattern Recognition and Artificial Intelligence, 2017, 30(5): 416-428.)

[18]马福民,陈静雯,张腾飞.基于双重粒化准则的邻域多粒度粗集快速约简算法[J].控制与决策,2017，32(6):1121-1127. (MA F M, CHEN J W, ZHANG T F. Quick attribute reduction algorithm for neighborhood multi-granulation rough set based on double granulate criterion [J]. Control and Decision, 2017, 32(6): 1121-1127.)

[19]LIN G, LIANG J, QIAN Y, et al. A fuzzy multigranulation decision-theoretic approach to multi-source fuzzy information systems [J]. Knowledge-Based Systems, 2016, 91: 102-113.

[20]XU W, GUO Y. Generalized multigranulation double-quantitative decision-theoretic rough set [J]. Knowledge-Based Systems, 2016, 105: 190-205.

[21]邢清华,刘付显.直觉模糊集隶属度与非隶属度函数的确定方法[J].控制与决策,2009,24(3):393-397. (XING Q H, LIU F X. Method of determining membership and nonmembership function in intuitionistic fuzzy sets [J]. Control and Decision, 2009, 24(3): 393-397.)