BTT-180飞行器滚转通道自动驾驶仪优化设计
崔晓曦,娄英明
(中国兵器工业导航与控制技术研究所,北京 100089)
0 引言
高超声速飞行器通常指飞行马赫数大于5的飞行器,主要包括可重复起降的航天运载器、高超声速导弹、跨大气层飞行器等。为保持速度,高超声速飞行器多需采用冲压发动机等只有单边攻角特性的吸气式发动机,为保证发动机进气性能不受影响,需采用正攻角飞行;为使飞行器具有大的机动性,多采用面对称布局,倾斜转弯(Bank to Turn,BTT)控制方式,通过将主升力面进行滚转以实现对纵向、侧向的同时控制。高超声速飞行器受发动机正攻角飞行及面对称布局的限制,需采用BTT-180控制方式,即当需用过载为负时(对应负攻角飞行),应将飞行器进行180°滚转后再拉过载[1],因此滚转通道自动驾驶仪的设计是BTT-180飞行器能否实现有效制导飞行的关键因素。BTT-180滚转通道自动驾驶仪的主要任务是让飞行器在最短的时间内利用有效的舵资源在有限的最大滚转角速度内实现快速滚转180°的急滚需求。本文从工程应用的角度出发,提出了两种滚转角指令优化方法,分别阐述了优化设计模型和设计方法,将设计结果进行对比并得到两种优化方法的优缺点对比结论,为有180°滚转需求的飞行器提出了有工程应用价值的滚转指令优化设计方法[2]。
1 模型建立
弹体坐标系为Oxbybzb,惯性坐标系为Oxyz。假设Oxb与Ox重合,Oyb与Oy重合。图1所示为飞行器正常飞行状态,图2所示为飞行器翻转飞行状态。
通常飞行器的滚转通道自动驾驶仪采用PID或PD控制,驾驶仪模型如图3所示[3]。
图3中,滚转通道自动驾驶仪舵机指令组成为
在实际工程中,在滚转180°时需要考虑下面2个问题:
(1)副翼舵限幅
由于机械结构所限,副翼的偏置范围有限,开始滚转时,由于驾驶仪中kp要远大于kd,dx几乎完全由比例项决定,此时误差信号γb-γc很大,舵机会迅速饱和并进入非线性,这是控制系统和舵系统不希望看到的。
(2)滚转角速度限幅
受限于惯性器件,滚转角速度有一定的策略范围,若滚转角速度ωx太大,则会超过惯性器件的角速度测量范围,甚至造成惯性器件损害[5]。
引入一个典型的滚转通道自动驾驶仪设计范例说明以上2个问题[6]:
kr=-2500,Tr=5,kd=0.0279,kp=0.2。假设舵限幅是在(-10°,10°),忽略惯性器件动力学特性,得到副翼和滚转角速度曲线如图4和图5所示。
由于滚转角指令和滚转角的误差太大,副翼偏角迅速达到饱和并进入非线性,在一定时间内维持最大值。在这个时间内,滚转角速度迅速达到了-750(°)/s,超过了一般的角速度陀螺的可靠测量范围。
可见,对于有180°滚转需求的飞行器,如果滚转角指令不进行优化,那么很难避免进入舵机非线性或达到惯性器件角速度饱和范围。
2 滚转角指令优化
本文提出了两种滚转角指令优化方法,一种是线性优化,另外一种是指数优化。
2.1 线性优化
线性优化方法是最直观、简洁的优化方法,并且广泛应用于实际工程中[4]。假设滚转角指令γc按一个固定的斜率从180°变化到0°,这种指令与斜坡输入类似[7]。由于滚转通道自动驾驶仪是I型系统,能够对斜坡输入实现无稳态误差的跟踪,因此线性优化的结果能够应用在滚转通道自动驾驶仪中[8]。
图 6 所示为滚转角指令线性优化的指令示意图。T时刻的滚转角指令gamac=0。
在(0,T)区间内的任意时刻t,滚转角指令为
其中,T是优化时间常数。
为了不影响驾驶仪的跟踪快速性,T由滚转通道自动驾驶仪闭环响应时间决定。
如果滚转通道自动驾驶仪的条件时间是ts那么T=ts。
2.2 指数优化
尽管线性优化方法简单明了,但是却有显而易见的缺点:最大滚转角ωx速度无法控制和预测。本节将详细介绍另外一种优化方法:指数优化的设计方法。设置最大滚转角速度为优化指标,指数优化方法可以精确地将ωx和δx控制在需要的范围内,并实现能量最小[9]。
指数指令公式为
γc(t)=γb0e-t/T
其中,γb0=180°,T是指数优化的时间常数。
对于图3所示的滚转通道自动驾驶仪,ωx可以写为如下与T相关的形式
ωx=g(t,T)
不失一般性,假设低成本的滚转角速率陀螺的测量范围为±(250~300(°)/s)。在控制系统设计时,我们保留一定的裕度,取ωx的限制范围为±(220(°)/s)。
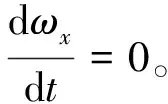
tmax(ωx)=f(T)
将tmax(ωx)代入ωx=g(t,T),得到关于T的等式
max(ωx)=g(f(T),T)=±220(°)/s
求解以上公式,可以得到max(ωx)与T的关系,这样可以建立起T与期望ωx最大值的关系。
kp和kd可以被写为阻尼比μ和带宽ωn的形式[10]。
假设阻尼比为一个定值,不同的带宽对应的时间常数如图7所示。
对上述曲线进行耦合,得到指数优化的时间常数与滚转通道自动驾驶仪闭环带宽的关系如下
下面对拟合公式的精度进行验证,结果如图8所示。可见,拟合公式与计算结果的重合度很好。
按照以上的步骤,可以对不同气动特性的滚转通道自动驾驶仪进行滚转角指令优化时间常数设计。
2.3 优化方法对比
以上面提到的滚转通道自动驾驶仪为例,假设飞行器需要从图 2的状态翻转到图 1的状态,线性与指数优化结果对比如图9~图12所示。
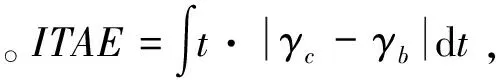

表1 ITAE 对比
可以得到两种优化方法的优劣对比如表2所示。

表2 优化方法对比
3 结论
综上所述,滚转指令优化是BTT-180飞行器滚转通道自动驾驶仪设计的重要内容。本文阐述了滚转指令优化的意义、方法和优化结果对比,并得到了不同优化方法的优缺点。当导弹的副翼舵效高,滚转角速率陀螺测量范围大,控制系统设计周期短时,建议使用滚转角指令线性优化设计方法;当导弹的副翼舵效相对较低,滚转角速率陀螺测量范围较小时,建议使用滚转角指令指数优化设计方法,并且应在设计时留有一定余量。
[1]Zarchan P. Tactical and strategic missile guidance[M]. Washington D C: American Institute of Aeronautics and Astronautics(AIAA), 2012.
[2]斯维特洛夫,戈卢别夫. 防空导弹设计[M]. 北京: 中国宇航出版社, 2004.
[3]Garnell P, East D J, Siouris G M. Guided weapon control systems(second revision) [M]. Beijing: Beijing Institute of Technology, 2004.
[4]Lestage R. Analysis of control and guidance of rolling missiles with a single plane of control fins[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit. Denver: AIAA, 2000: 14-17.
[5]朱志刚, 周凤岐. BTT导弹滚转通道变结构最终滑态控制系统设计[J]. 西北工业大学学报, 1995,13(2): 292-296.
[6]陈新海, 李育俊, 周军. 自适应控制及应用[M]. 西安: 西北工业大学出版杜, 2000.
[7]王琦, 崔立君. 飞航导弹横测通道协调变结构飞行控制系统设计[J]. 计算机测量与控制, 2007,15(12): 1756-1757.
[8]杨军, 杨晨, 段朝阳. 现代导弹制导控制系统设计[M]. 北京: 航空工业出版社, 2005.
[9]范军芳, 林德福, 祁载康, 等. 两回路自动驾驶仪设计与分析[J]. 系统工程与电子技术, 2008,30(12): 2447-2450.
[10]郑大钟. 线性系统理论(第2版)[M]. 北京: 清华大学出版社, 2002.

