作动器输出机构刚度优化设计与仿真分析
张新华,刘 源,张兆凯,黄 建
( 北京自动化控制设备研究所,北京 100074)
0 引言
电动作动器作为飞控系统的主要部件,对其动态特性有着较高的要求[1]。在电动作动器的实际使用中,当其舵偏角、最大舵偏角速度、频带、线性度和超调量等性能指标比较满意的情况下,仍会出现一些新的问题,这些问题存在的主要原因之一就是作动器的刚度特性不能满足要求[2]。刚度太差则极易引发舵面的颤振。当颤振发生时,副翼或舵面有很大的偏转,舵翼发生振动,振幅很大,频率很高,极易发生危险[3]。
另外,发散、颤振、气动伺服弹性不稳定等气动弹性问题往往要等到导弹飞行试验才暴露出来,而一旦在飞行中发生这类问题,则将直接导致飞行失利[4]。因此,在导弹方案设计阶段就需要对气动弹性问题进行研究,以避免由于导弹方案设计不当而导致气动弹性问题的发生[5-11]。
作动器的刚度是导弹气动伺服弹性问题的重要影响因素之一,若刚度较低则使导弹易发生颤振风险[12]。作动器连杆机构刚度的大小是影响其整体机械刚度的主要因素之一,而连杆机构的主要组成部分为输出机构,因此,输出机构刚度直接影响作动器的整体性能[13-15]。本文对作动器输出机构的刚度做重点研究,旨在优化作动器的整体机械刚度,为工程应用提供理论依据。
1 作动器连杆机构刚度的理论分析
电动作动器的连杆机构如图1所示,考虑输出机构与转接杆的弹性变形时,输出机构的弹性变形可以看作是轴体空心圆柱的扭转变形与摇臂变截面悬臂梁变形的组合变形;转接杆的变形可以看作是简单的拉压变形;整个连杆机构的变形则是这三种变形综合作用的结果,可使用组合变形的叠加原理对其进行分析。下面对连杆机构的机械刚度进行详细推导。
1.1 作动器输出机构轴体的扭转变形
由材料力学可知,在圆轴的两端作用扭转力偶时,始末截面间绕轴线的相对转角可以使用式(1)计算,其中,l为圆轴的有效长度,M为扭转力偶,G为材料的弹性模量,Ip为圆轴截面的极惯性矩。
(1)
对于空心圆轴,截面的极惯性矩为
(2)
其中,D和d分别为空心圆截面的外径和内径,α=d/D。
则对于等直圆轴的相对转角即为
(3)
1.2 作动器输出机构摇臂的变截面悬臂梁变形
摇臂的数学模型可以简化成图2所示。由材料力学可知,挠曲线的近似微分方程为
(4)
将挠曲线近似微分方程经过两次积分可以得到挠曲线方程为

(5)
设分布力的线密度为q,则在分布力范围内外力偶矩为
(6)
由于悬臂梁的截面是矩形变截面,故横截面对中性轴的惯性矩为
(7)
则挠曲线的方程为

(8)



=W+P+Q
(9)
其中:

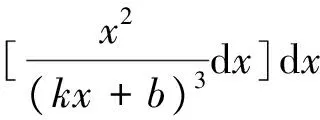

则可得挠曲线方程为
(10)
对挠曲线方程一阶求导,可以得到
(11)

(12)
则可以求得x=l时,悬臂梁的挠度为
ωmax=ωx=l
(13)
以此可得由摇臂变截面悬臂梁的变形引起的转角变化为
(14)
采用叠加原理,可以得到整个连杆机构的机械刚度的计算方式为
(15)
对以上理论计算方法作以下几点补充说明:
1)由于把摇臂简化成悬臂梁计算时忽略了销孔的存在,而是直接把力加载在悬臂梁的外缘中性面上,所以实际计算的最大挠度值比实际值和仿真的结果相比要小,即最终理论计算的φ2值要小;
2) 与1)同理,转接杆的理论变形量要比实际测量值和仿真值小,即理论计算的φ3要小;
3) 由于理论计算中没有考虑销的变形量和接触刚度的影响,故最终计算的φ值要小。
综上所述,运用理论计算的连杆机构的机械刚度值比实际测量值和仿真值要大。实际计算中,由于转接杆的变形量非常小,故近似认为舵机输出机构的机械刚度即为连杆机构的机械刚度。
2 作动器输出机构的刚度优化设计
把理论计算公式通过编程处理,代入常量,改变k或t,可以发现,当|k|或t增大时,变截面悬臂梁的最大挠度越小。因此在输出机构的实际设计中重点考虑这2个尺寸,以提高输出机构的机械刚度,图3所示为作动器输出机构的两种不同设计形式。
图3所示的作动器输出机构,属于初步优化设计,考虑到输出机构有一定的摆角范围,为防止输出机构顺时针旋转到最大摆角时,转接杆与输出机构轴体发生干涉,需要计算出连杆宽度的最大值。
作动器的零位定义为摇杆在竖直方向时的角度。此处定义机械限位角度为Φ,设输出机构轴体半径为R,连杆中心线在坐标系下的斜率为k,连杆的宽度为2d,如图4所示。
当输出机构的摇杆刚好达到机械限位时,连杆与滚珠丝杠轴向夹角正切值为
(16)
则连杆中心线在坐标系下的直线方程为
y=k(x+L2cosγ-L1sinφ)+L
(17)
此时,连杆与输出机构轴体不干涉的条件为
(18)
在实际设计中,综合考虑各种因素后,选择双摇臂的单个厚度为4mm,总厚度为8mm,比改进前输出机构的摇臂厚2mm,可以在较大程度上改善悬臂梁处的机械变形。另外选择摇臂的伸展角为50°, 可以较大地减小变截面悬臂梁处受力时的最大挠度。综合考虑连杆与输出机构轴体的干涉与摇臂的变形,适当减小摇臂伸展角处过渡弧的半径为6mm,比原过渡弧半径少3.5mm。
此外,优化前的设计中,输出轴体明显偏长,其伸出轴承了一段距离,这段距离的输出轴体并没有对整个作动器的机械刚度或者抗弯曲刚度起到很大的作用,故适当减小其长度,不仅可以减小作动器的质量,还可以给输出机构的安装带来较大便利。
另外,采用齿轮与轴体分离设计,在安装输出机构时,可以先安装轴体,后安装齿轮,从而达到在不改变现有壳体设计的情况下,顺利安装优化设计后的输出机构。分离的轴体与齿轮通过沉头螺钉连接,沉头螺钉还起到定位的作用。
3 作动器输出机构刚度仿真分析
对现有的与优化后的作动器输出机构模型简化处理后,在Ansys中采用自动划分网格的方法,定义输出轴摇臂受到300N·m的负载,得到仿真的结果如图5所示。
由表1可见,优化设计后作动器输出机构摇臂处的变形量比优化前减少38.92%,通过计算可得优化设计后舵机输出轴的机械刚度比优化前提升了63.72%,且质量减小了0.98%。优化后的设计对舵机输出轴摇臂的底部作了加强处理,起到了加强筋的作用,在一定程度上阻止了摇臂的弹性变形,因此较大地提升了输出机构的机械刚度。

表1 输出机构优化前后对比
4 结论
1)运用扭转变形与变截面悬臂梁理论详细推导了作动器输出机构的机械刚度计算方法,提出影响输出机构机械刚度的2个主要因素——厚度和变截面斜率;
2)对作动器输出机构进行系统地优化设计,在提高输出机构刚度的同时避免出现安装干涉与质量增加的情况;
3)通过仿真发现,优化设计后,作动器输出机构的机械刚度得到了较大的提升,有效地提升了作动器的整体机械刚度,具有较高的实际工程应用价值。
[1]张新榃, 吴志刚, 杨超. 考虑舵机动态特性的颤振分析[C]// 第十一全国空气弹性学术交流会. 2009.
[2]吴娟, 张家盛, 康光会. 舵机系统动刚度的分析研究[J]. 科学技术与工程, 2008, 8(4):1124-1128.
[3]何锃. 理论力学[M]. 武汉: 华中科技大学出版社,2007.
[4]张盛楠. 电动伺服系统非线性建模、仿真与测试技术[D]. 北京自动化控制设备研究所, 2011.
[5]刘源, 王永乐, 曹东海,等. 一种伺服机构刚度计算方法[J]. 导航定位与授时, 2014, 1(2):46-49.
[6]Lin Y, Baumann E, Bose D M, et al. Tests and techniques for characterizing and modeling X-43A electromechanical actuators[R]. NASA/TM-2008-214637. 2008:21-27.
[7]Layton D S, Gaines V G. F-22 Actuator Dynamic Stiffness (Impedance) Testing[C]// 48thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. 2007: 1792.
[8]张新华, 黄建, 张兆凯,等. 大惯量下电动伺服机构非线性特性与控制方法研究[J]. 导航定位与授时, 2017, 4(2):41-47.
[9]张新华,杨瑞峰.含间隙的电动伺服机构非线性振荡研究[C]//第五届全国振动利用工程学术会议暨第四次全国超声电机技术研讨会, 2012:825-828.
[10]李友年, 陈星阳. 舵机间隙环节对控制系统的影响分析[J]. 航空兵器, 2012(1):25-27.
[11]李晓贞, 朱如鹏, 李政民卿,等. 齿面摩擦对面齿轮传动系统振动特性的影响分析[J]. 振动工程学报, 2014, 27(4):583-588.
[12]张劲夫, 许庆余, 张陵. 考虑连杆柔性和运动副粘性摩擦的曲柄滑块机构的动力学建模及计算[J]. 航空学报, 2001, 22(3):274-276.
[13]肖前进, 贾宏光, 章家保,等. 电动舵机伺服系统非线性辨识及补偿[J]. 光学精密工程, 2013, 21(8):2038-2047.
[14]夏栋.电动舵机伺服机构动力学特性研究[D]. 哈尔滨:哈尔滨工业大学, 2014.
[15]李会娜, 高庆, 肖健,等. 空气舵-伺服系统动态特性试验技术研究[J]. 强度与环境, 2013(2):7-11.

