正六面体工装误差对光纤惯组加速度计零偏标定精度影响分析
姚 勤,胡梦纯,何子辉
(1.海军驻上海地区航天系统军事代表室,上海201109; 2. 上海航天控制技术研究所,上海201109; 3.上海惯性工程技术研究中心,上海201109)
0 引言
陀螺和加速度计是惯性测量组合的核心元件。惯性测量组合性能的好坏直接影响导航精度。要提高惯组的使用精度,一方面要提高陀螺和加速度计的自身精度,另一方面还需要提高惯组的标定精度。提高标定精度需要分析各误差源对标定参数产生的影响,对基于大理石平板正六面体工装的标定进行分析,六面体工装的精度会对标定结果产生影响。本文通过评估工装精度对标定结果影响的量化关系,提出一种减小工装误差影响的光纤惯组标定解算方法。文献[1]、文献[2]针对转台误差对标定结果的影响进行分析[1-2],文献[3]研究了基于离心机的IMU标定及误差分析方法[3],而本文使用的标定方法并未使用转台和离心机,而是采用大理石平板与正六面体工装进行标定,针对正六面体工装误差的文献涉及较少,有必要分析该方法中正六面体工装误差导致的标定误差。
1 光纤惯组输入输出数学模型
标定模型对于标定方法的选择、IMU性能评估以及系统的误差分配具有重要意义[4],下面讨论光纤惯组的标定数学模型。
光纤惯组中的陀螺和加速度计分别为光纤陀螺和石英挠性加速度计,工程上通常使用一阶线性方程描述光纤陀螺和石英挠性加速度计的误差模型。分别对陀螺仪和加速度计建立输入输出数学模型[5-6]。
光纤陀螺标度因数非线性高,正负不对称性好,零偏稳定性好,因此可将陀螺单表的输入输出模型近似描述为一阶形式。陀螺组合输入输出模型用一阶线性方程描述为:
(1)
式中:Ngx、Ngy、Ngz为各轴陀螺单位时间输出的脉冲数,单位bit/s;kgx、kgy、kgz为各轴陀螺的标度因数,单位bit/(°);Egqp(p、q=x,y,z)为惯组各测量轴相对各轴陀螺敏感轴由于安装误差导致的交耦系数,简称安装误差;Egqp为惯组p轴相对q轴陀螺的耦合;Dgx、Dgy、Dgz为各轴陀螺的零偏,单位(°)/s;ωx、ωy、ωz为外施角速率在惯组x、y、z轴上的分量,单位(°)/s。
加速度计二次项系数忽略不计,加速度计组合输入输出模型用一阶线性方程可表示为:
(2)
式中:Nax、Nay、Naz分别为各轴加速度计单位时间输出的脉冲数,单位bit/gs;kax、kay、kaz分别为各轴加速度计的标度因数,单位bit/gs;Eaqp(p、q=x,y,z)为惯组各测量轴相对各轴加速度计敏感轴由于安装误差导致的交耦系数,简称安装误差;Eaqp为惯组p轴上的输入对q轴加速度计的耦合;Dax、Day、Daz为各轴加速度计的零偏,单位g;fx、fy、fz为外施加速度在惯组x、y、z轴上的分量,单位g。
2 基于大理石平板正六面体工装的标定与解算
惯组的标定方法有利用转台的方法[7-8],利用六面体工装的方法[9],使用摄影技术的方法[10],基于多位置旋转的现场标定法[11]等,用标定方法多为速率法与位置法,位置法又分为6位置法[12-13]、12位置法[5-6]、20位置法[14]等。
基于大理石平板正六面体工装的标定方法采用了速率法与位置法,速率法采用在高精度大理石平板上手动正反转3圈的方式进行标定,位置法为12位置法。速率法可标定出陀螺标度因数、安装误差[15];位置法可标定出陀螺零偏、加表标度因数、安装误差、零偏。本文主要对正六面体工装误差对加速度计标定零偏误差的影响进行分析,因此仅分析位置法。
位置法编排为12位置,初始位置为天东北,按照X轴朝天、X轴朝地、Y轴朝天、Y轴朝地、Z轴朝天、Z轴朝地的顺序对12位置进行排列,得到标定顺序,如表1所示。

表1 12位置标定顺序
将12位置加速度计和陀螺仪输入代入模型中,利用最小二乘法可以求出:
(3)
(4)
(5)

归一化可得各轴加速度计标度因数为
(6)
式中:q=x,y,z。
各轴加速度计安装误差为
Eaqp=Kaqp/kgq
(7)
式中:j=1~12;p=x,y,z;q=x,y,z。
根据加速度计各位置各轴输出可得
可求得各轴加速度计零偏为
(8)
式中:j=1~12,q=x,y,z。
还有一种零偏的计算方法为12位置二向法,求各轴零偏时,只考虑敏感轴朝天朝地的位置进行解算。
(9)
(10)
(11)
3 标定误差分析
惯组测试标定用工装为六面体,惯组标定时需要安装在六面体工装内,再在大理石平板上进行标定。六面体工装外表面由6个基准面组成。六面体内由1个或多个安装基准面组成,这些安装基准面能够保证每次惯组安装在六面体工装内的一致性,本文不对六面体内的基准面误差以及大理石平板的误差影响进行分析。
假设六面体工装是以底面C为基准加工其他表面,表2所示为六面体工装各面需加工的精度项目及引起的误差角。根据惯组测试标定的误差模型进行12位置法翻转时会引入工装的误差,直接影响惯组测试标定结果,使得加速度计的标定结果变差,具体分析如表2表示。
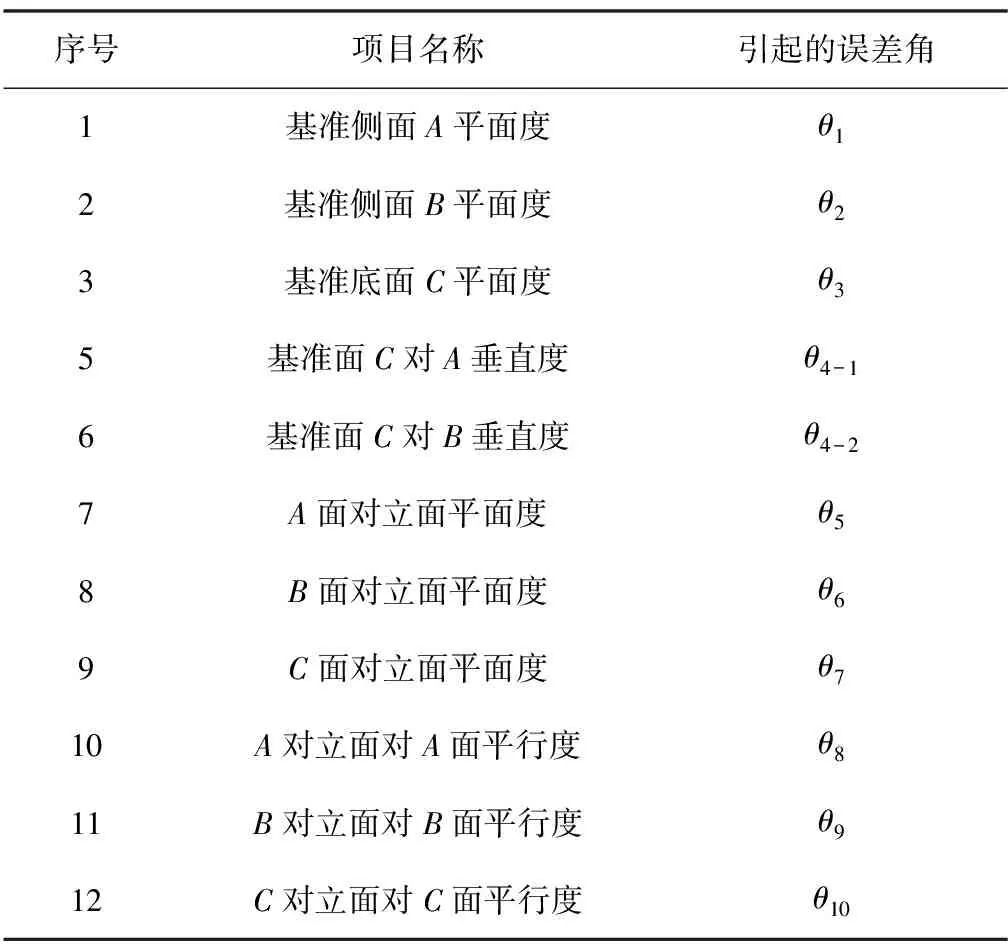
表2 六面体工装误差项目
假设惯组X轴向垂直C面,指向C面对立面;Y轴向垂直A面,指向A面对立面;Z轴向垂直B面,指向B面对立面,具体如图1所示。
对六面体工装精度对12位置法标定中加表零偏值的影响进行分析,根据表2,考虑六面体工装误差时各位置加速度计各轴的参考输入如表3所示。

表3 十二位置标定各轴参考输入
将各轴参考输入加速度代入加表组合模型中,可得加表的采样输出如式(12)
(12)
式中,加表输出为采样输出,标度因数、安装误差、零偏均为真实值。为简化分析,令表1中各误差角均设置为等值θ。解算标定参数时,根据第3节中的公式,可推导出考虑六面体工装误差后标定出的零偏测量如下。
12位置法
(13)
12位置二向法
(14)
(15)
(16)
12位置法解算出的零偏误差为
(17)
12位置二向法解算出的零偏误差为
(18)
忽略小量,可推知两种零偏算法的误差值分别为:
(19)
ΔDa2≈0
(20)
12位置解算方法中引入的误差与工装精度成正比,12位置二向法中引入的误差均为小量,可忽略不计。
由理论推导可知,当考虑六面体工装误差时,12位置法解算出的零偏会引入六面体工装误差,而采用12位置二向法解算出的加表零偏基本不引入六面体工装误差。
4 仿真分析与验证
对12位置标定进行仿真,加速度计测量噪声设置为10μg高斯白噪声。正六面体工装长度为400mm,六面体工装误差项目中平面度、垂直度、平行度均为0.04。按表1所示12位置,每个位置静态采集100s,采样周期20ms,用于加速度计标度因数、安装误差、零偏的标定,加速度计标定参数真值设定如表4所示,仿真结果如表5所示,标定结果误差对比如表6所示。

表4 加速度计标定参数真值设定

表5 加速度计标定参数仿真结果

表6 零偏误差对比
由仿真结果可以看出,考虑六面体工装误差的情况下,用12位置法解算出的零偏与真值偏差比用12位置二向法解算出的零偏与真值偏差大。
5 结论
本文针对采用大理石平板正六面体工装对惯组12位置法标定进行分析,考虑工装误差,量化分析并比较了采用两种解算方法时工装的精度对加表零偏产生的影响,为如何根据标定精度要求反提工装精度要求提供理论依据,并提出了一种减小加表零偏标定误差的解算方法。
当长宽高为400mm的工装平面度、垂直度、平行度误差均为0.04时,采用12位置法解算加速度计零偏的标定误差达到0.0001g量级;而采用12位置二向法解算加速度计零偏,误差为10-7g量级。可以看出,12位置二向法解算出的加速度计零偏误差远小于采用12位置法解算出的加速度计零偏误差。为减小工装误差的影响,解算加速度计零偏时可采用12位置二向法。
[1]丁枫,冯丽爽,晁代宏,等.转台安装误差对光学捷联惯导标定的影响分析[J].弹箭与制导学报,2013,33(1):19-24.
[2]聂梦馨, 吕品, 赖际舟,等. 一种光纤IMU的双轴非定向标定方法[J]. 电子测量技术, 2014, 37(8):123-128.
[3]赵剡, 张少辰, 胡涛. 惯性测量组件离心机标定及误差分析方法[J]. 北京理工大学学报, 2015, 35(4):414-420.
[4]赵桂玲, 姜雨含, 李松. IMU标定数学建模及误差分析[J]. 传感技术学报, 2016, 29(6):886-891.
[5]胡梦纯, 徐挺, 黄云柯,等. 冗余结构光纤陀螺捷联惯组标定优化方法研究[J]. 上海航天, 2016, 33(s1):134-139.
[6]魏莉莉, 黄军, 傅长松,等. 带斜置元件的光纤陀螺捷联惯组标定方法[J]. 中国惯性技术学报, 2015(1):14-19.
[7]李政, 张志利, 周召发. 基于双轴位置转台的光纤陀螺惯组标定方法[J]. 压电与声光, 2016(4):607-610.
[8]童树兵, 张志利, 周召发,等. 一种基于双轴位置转台的IMU快速标定方法[J]. 压电与声光, 2016, 38(5):815-818.
[9]彭孝东, 张铁民, 李继宇,等. 三轴数字MEMS加速度计现场标定方法[J]. 振动、测试与诊断, 2014, 34(3):544-548.
[10]江来伟, 崔希民, 袁德宝,等. 惯性测量单元基准面与载体平台的标定方法研究[J]. 测绘工程, 2015(3):16-20.
[11]王坚, 梁建, 韩厚增. 低成本IMU的多位置旋转现场标定方法[J]. 中国惯性技术学报, 2017, 25(3):294-298.
[12]乌伟, 赵严, 宁永权,等. 微惯性测量单元的标定技术研究[J]. 电光与控制, 2013(8):54-57.
[13]李璞, 王丽华, 李明. 重复标定的惯组误差模型系数计算方法[J]. 导弹与航天运载技术, 2012(3):34-37.
[14]董春梅, 任顺清, 陈希军. 基于三轴转台误差分析的IMU标定方法[J]. 系统工程与电子技术, 2016, 38(4):895-901.
[15]林强. 高精度光纤陀螺标度因数测试研究[J]. 现代导航, 2013(3):186-190.

