长航时高精度惯导系统姿态阵的四种解算方法

何虔恩，曾聪杰，林志贤，刘开进

(1.福州大学 物理与信息工程学院，福州350116; 2.福建星海通信科技有限公司，福州350001)

0　引言

惯性导航解算过程需要利用姿态阵将平台系(P系，即惯性器件安装的坐标系)中的比力矢量转换到导航坐标系下，再进行积分运算，依次得到速度和位置信息。因此，要得到高精度的导航参数，需要有高精度的姿态阵。在捷联式惯导系统中，惯性器件与载体固连，平台系姿态变化剧烈，因而对姿态阵解算的精度和实时性要求较高。在平台式惯导系统中，由于大部分载体角运动被框架伺服系统隔离，平台姿态变化缓慢(主要由伺服控制误差、陀螺漂移和导航坐标系角运动等引起)，降低了对姿态阵解算的实时性要求，但对解算精度的要求仍然较高。另外，惯导系统初始对准通常需要建立系统的线性化误差模型，而不同的姿态阵解算方法，对应的线性化误差模型及其精度是不同的。因此，为了实现长航时高精度的惯性导航系统，设计高精度的姿态阵解算方法至关重要。

针对捷联式惯导系统的姿态解算方法，在20世纪60年代末和70年代初，Savage[1]、Jordan[2]和Bortz[3]先后提出和发展了双速捷联算法，许多研究人员就该方法进行了相关补偿算法的研究。国内学者针对姿态解算方法开展了深入的研究工作[4-15]。纵观公开的文献资料，姿态解算的方法主要有以下四种：1)欧拉角法、改进欧拉角法；2)方向余弦法；3)四元数法；4)等效转动矢量法[5]。其中，等效转动矢量法是一种可以有效克服载体运动中不可交换误差的算法。欧拉角法、方向余弦法、四元数法是三种常用方法(又分别称为三参数法、九参数法和四参数法)。相关学者对这三种解算方法进行了对比研究，具体来说，欧拉角法只需要解3个微分方程，但不可避免地会出现奇点；方向余弦法避免了奇点问题，却需要解9个繁杂的方程；四元数法既避免了奇点问题，同时计算量也不大，因此，它成为捷联惯导系统中姿态解算最常用的方法。已有研究只考虑了2个坐标系之间一步旋转到位的情况，而从数学层面上讲，一个坐标系到另一个坐标系可以一步到位旋转，也可以通过引入中间坐标系，将旋转过程分成若干步完成，此时，对应的姿态阵(即方向余弦阵)被分解成若干个子矩阵的乘积，各个子矩阵分别解算，已有研究并没有解决哪种旋转方法对应的姿态阵解算精度更高的问题。

本文通过分解姿态阵以及分别采用Euler角和四元数描述姿态参数，建立解算姿态阵的四种方法——整体-Euler角法、整体-四元数法、分解-Euler角法和分解-四元数法，并分别对这四种方法进行对比分析。在相同初始条件和满足各自约束条件的情况下，分别对这四种方法中的姿态模型进行扰动，并研究相应线性化误差模型的精度及其影响因素，再利用数值仿真法对四种姿态解算方法的结果及对应的线性化误差模型的精度进行比较分析。

1　姿态阵的四种解算方法

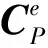
1.1　整体-Euler角法

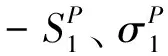
(1)

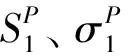
(2)

1.2　分解-Euler角法

(3)

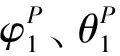
(4)

又知：

(5)

1.3　整体-四元数法

(6)

根据四元数与方向余弦阵之间的关系

(7)

可得

因此，将式(6)展开并整理可得

(8)

给定四元数初值和每个时刻的P系角速度，采用数值积分算法即可递推算出各个时刻的四元数向量，进而可得姿态阵为

(9)

1.4　分解-四元数法

(10)

同理，

(11)

2　扰动线性化模型及其精度分析

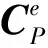
2.1　整体/分解-四元数法与整体/分解-Euler角法的等价性

利用方向余弦阵与四元数之间的关系式(7)可得

将四元数微分方程式(8)代入上式，整理得

证毕。

综上，整体/分解-四元数法与整体/分解-Euler角法等价。

2.2　整体-Euler角法与分解-Euler角法的比较

基于第2.1节的证明，不失一般性，下面集中精力讨论整体-Euler角法与分解-Euler角法对应的两种扰动线性化模型。

2.2.1整体-Euler角法的扰动线性化模型

对方程式(1)两边进行扰动并略去二阶项，整理后可得

(12)

为了便于可观测性分析和初始对准滤波器设计，希望扰动线性化模型的齐次部分是常系数的，因此，方程式(12)需要进一步简化为

(13)

2.2.2分解-Euler角法的扰动线性化模型

对方程式(3)两边进行扰动并略去二阶项，整理后可得

(14)

为了便于可观测性分析和初始对准滤波器设计，希望扰动线性化模型的齐次部分是常系数的，因此，方程式(14)需要进一步简化为

(15)

2.3　分析比较

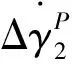
综上可见，分解-Euler角法对应的常系数扰动线性化模型(15)比整体-Euler角法对应的模型(13)具有更高的精度。

表1　扰动线性化模型包含的齐次变系数部分的误差项

3　计算机仿真分析

(16)

(17)

(18)

这样，前述四种方法可互相比较。

3.1　四种方法的解算结果比较

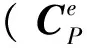
3.2　四种方法对应的扰动线性化模型精度比较

仿真步骤(纬度设为北纬40°)：

(1)生成整体-Euler角法对应误差的参考轨迹

(2)生成整体-Euler角法对应扰动线性化模型的轨迹

(3)求模型线性化误差造成的轨迹偏差

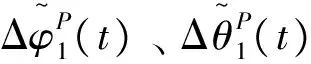
4　结论

姿态阵解算精度对长航时高精度惯导系统的使用性能有着重要的影响。通过分解姿态阵以及分别采用Euler角和四元数描述姿态参数，建立了解算姿态阵的整体-Euler角法、分解-Euler角法、整体-四元数法和分解-四元数法；证明了整体/分解-Euler角法与整体/分解-四元数法的等价性；对相应的扰动线性化模型的精度进行了对比分析，数值仿真结果验证了整体/分解-Euler角法与整体/分解-四元数法的等价性，同时表明：分解法对应的线性化误差模型的精度优于整体法，这对高精度惯导的初始对准和导航算法设计具有重要的指导意义。

[1]Savage P G. Strapdown inertial navigation integration algorithm design part 1:Attitude algorithms[J]. Journal of Guidance Control & Dynamics, 1998, 22(2):19-28.

[2]Jordan J W. An accurate strapdown direction cosine algorithm[R]. Report TND-5384, NASA, Washington, 2001.

[3]Bortz J E. A new mathematical formulation for strapdown inertial navigation[J]. IEEE Transactions on Aerospace & Electronic Systems,1971(1):61-66.

[4]赵晗, 汪立新, 赵曦晶,等. 基于间隔子样旋转矢量的SINS圆锥误差补偿[J]. 压电与声光, 2015, 37(1):158-161.

[5]雷鸣, 蔡体菁, 李勇建. 捷联惯导系统算法比较研究[J]. 中国惯性技术学报, 2002, 10(1):20-24.

[6]Luo J, Gang Y, Tang L J. Attitude estimation of quad-rotor aircraft based on hybrid filter[J]. Measurement & Control Technology, 2017,36(7):5-8,12.

[7]Chang L, Li J, Chen S. Initial alignment by attitude estimation for strapdown inertial navigation systems[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(3):784-794.

[8]Wu Z, Yao M, Ma H, et al. Improving accuracy of the vehicle attitude estimation for low-cost INS/GPS integration aided by the GPS-measured course angle[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2):553-564.

[9]Valenti R G, Dryanovski I, Xiao J. Keeping a good attitude: A quaternion-based orientation filter for IMUs and MARGs[J]. Sensors, 2015, 15(8):19302-19330.

[10]Tanveer F, Kadri M B, Aziz N, et al. Fuzzy based tuning of a sensor fusion based low cost attitude estimator[C]//6thInternational Conference on Innovative Computing Technology(INTECH). IEEE, 2016:672-676.

[11]Jing X, Cui J, He H, et al. Attitude estimation for UAV using extended Kalman filter[C]//29thChinese Control and Decision Conference(CCDC). IEEE, 2017:3307-3312.

[12]Li X, Chen M, Zhang L. Quaternion-based robust extended Kalman filter for attitude estimation of micro quadrotors using low-cost MEMS[C]//35thChinese Control Conference(CCC). IEEE, 2016:10712-10717.

[13]Tong X, Li Z, Han G, et al. Adaptive EKFbased on HMM recognizer for attitude estimation using MEMS MARG sensors[J]. IEEE Sensors Journal, 2017(99):1.

[14]Zhang X, Yang Z, Zhang T, et al. An improved Kalman filter for attitude determination of multi-rotor UAVs based on low-cost MEMS sensors[C]//IEEE Chinese Guidance, Navigation and Control Conference(CGNCC). IEEE, 2016:407-412.

[15]Ren X, Liu S. Combiningextended Kalman filter with complementary filter for UAV attitude estimation based on MEMS MARG sensors[C]// International Forum on Management, Education and Information Technology Application. 2016:746-752.

[16]高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.