旋转式SINS的自标校技术研究

王　坤，殷廷巍，奔粤阳

(1.哈尔滨工程大学 自动化学院，哈尔滨 150001;2.大连426厂，大连 116005)

0　引言

捷联惯导系统是一种自主式导航定位系统，短期内精度高，稳定性好[1]，但其定位误差会随着时间发散[2-4]，惯性器件误差是影响其发散的关键因素，而且该误差量在实际使用中会产生微小变化。为提高惯导系统的导航精度，需要对惯性器件误差进行现场标校[5]。双轴旋转式惯导系统就是通过转位机构在不同的转位方案下，充分激励出惯性器件误差，并通过Kalman滤波进行估计补偿[6]。

目前，系统级标定的理论研究已经趋于成熟，文献[2]提出了10位置连续旋转方案，并利用Kalman滤波进行误差估计，但其稳定时间较长。文献[3]给出了平台多位置快速自标定方法，但没有分析转轴精度对估计精度的影响。本文建立了IMU误差模型，推导了双轴旋转捷联惯导系统误差公式，建立了Kalman状态方程，并提出一种8位置双轴标定方案，对惯性器件误差进行仿真分析，由实验结果充分证明其有效性和可行性，对于高精度惯导系统，具有一定的工程意义。

1　旋转调制惯导原理与双轴旋转式SINS的自标校方案设计

1.1　系统常用坐标系

1)地理坐标系(t系)——oxtytzt

地理坐标系是原点o位于地球表面任意一点，oxt指向水平东向，oyt轴指向水平北向，ozt沿垂线方向指向天，通常称为东北天坐标系[7]。

2)导航坐标系(n系)——oxnynzn

根据惯导系统的工作需求提出了导航坐标系的概念。将地理坐标系作为导航坐标系，这种导航坐标系称为当地水平固定指北方位坐标系。

3)载体坐标系(b系)——oxbybzb

载体坐标系是固连在载体上的坐标系。载体坐标系的坐标原点o位于载体的重心处，纵轴oyb在甲板平面指向舰首，横轴oxb指向其右舷，ozb垂直于oxbyb构成右手坐标系[7]。

4)惯性测量单元坐标系(s系)——oxsyszs

惯性测量单元坐标系又称IMU坐标系，为旋转调制系统需求设定的坐标系。坐标系的原点位于惯性测量组件的重心，三轴指向为惯性器件敏感轴方向[8-10]。

旋转式SINS捷联惯导系统主要是靠不同转位方案激励出惯导器件的误差，再通过Kalman滤波对其误差状态变量进行估计，对其误差结果进行补偿，从而提高捷联惯导系统的输出精度。另外，基于实际情况考虑，为提高系统的可靠性，降低对转位机构的要求，通过最少的转动次数和较短的转动达到最优的误差估计效果，本文基于该设计原则，设计了3组转位方案。

1.2　双轴4位置旋转方案的设计

双轴4位置旋转方案的具体设计如下：

由初始位置1绕ys轴按正向旋转90°后到位置2；由位置2绕xs轴按正向旋转180°后到位置3；由位置3绕ys轴按反向旋转90°后到位置4；由位置4绕xs轴按反向旋转180°后到初始位置1，转位方案如图1所示。

1.3　双轴6位置旋转方案的设计

双轴6位置旋转方案的具体设计如下：

由初始位置1绕ys轴按正向旋转90°后到位置2；由位置2绕ys轴按正向旋转90°后到位置3；由位置3绕xs轴按正向旋转180°到位置4；由位置4绕ys轴按反向旋转90°到位置5；由位置5绕ys轴按反向旋转90°到位置6；由位置6绕xs轴按反向旋转180°到初始位置1，旋转方案如图2所示。

1.4　双轴8位置旋转方案的设计

双轴8位置旋转方案的具体设计如下：

由位置1绕xs轴按正向旋转180°后到位置2；由位置2绕xs轴按正向旋转90°后到位置3；由位置3绕xs轴按反向旋转180°后到位置4；由位置4绕xs轴按反向旋转90°后到位置1；由位置1绕ys轴按正向旋转90°后到位置5；由位置5绕xs轴按正向旋转180°后到位置6；由位置6绕xs轴按正向旋转90°后到位置7；由位置7绕xs轴按反向旋转180°后到位置8；由位置8绕xs轴按反向旋转90°后到位置5；由位置5绕ys轴按反向旋转90°后到位置1，旋转方案如图3所示。

2　SINS的数学模型与Kalman滤波方法

捷联惯导的误差方程是研究捷联惯导系统的基础，本文以东北天坐标系为参考系[11]，建立了其捷联惯导系统的速度、位置和姿态误差方程[12]，以便对惯性器件进行误差补偿，并建立Kalman滤波方程，通过转位方案的激励[13-14]，对器件误差进行估计补偿，达到最优效果。

2.1　速度误差方程

速度误差定义为

δvn=vc-vn

(1)

式中，vc为计算坐标系下计算的速度。

式(1)两边同时对求导

其中：

(2)

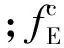
由于陀螺漂移和计算误差的存在，计算坐标系c系和导航坐标系n系之间存在着小角度的误差量φE、φN、φU，称为姿态误差角。且φE、φN、φU为小角度，有sinφ≈φ，cosφ≈1(其中φ=φE,φN,φU)成立，计算坐标系c系和导航坐标系n系之间转换关系可化简为

(3)

得

(4)

定义位置误差项为：

(5)

其中，L、λ分别为实际位置的纬度、经度。

(6)

利用式(4)、式(5)和式(6)可得SINS速度误差方程[5]：

(7)

2.2　位置误差方程

位置误差即经纬度误差和高度误差，是由于载体在东向、北向和天向的速度存在误差引起的。经纬度的变化率和载体线运动的关系为：

(8)

(9)

将式(5)求导得：

(10)

将式(2)、式(6)、式(8)和式(9)代入式(10)中，可得SINS位置误差方程：

(11)

2.3　姿态误差方程

捷联惯导系统的姿态误差角是通过方向余弦法所得到的计算地理坐标系与真实地理坐标系间的角度关系[15]。

平台运动基本方程为：

(12)

其中，εx、εy、εz为陀螺漂移引起的误差在导航坐标系的等效值；ωx、ωy、ωz为地理坐标系旋转角速度，且有：

(13)

将式(13)代入式(12)可得姿态误差方程：

(14)

2.4　Kalman滤波模型

建立旋转式光纤陀螺捷联惯导系统的Kalman滤波方程，其中状态方程为

(15)

其中，X(t)为t时刻系统的状态向量，F(t)为系统的状态转移矩阵，G(t)为系统的噪声驱动阵；W(t)为系统噪声向量。

本文的系统的状态向量为

(16)

系统的噪声向量为

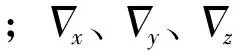
以速度误差作为量测量，则系统的量测方程为

Z(t)=H(t)X(t)+V(t)

(17)

其中，Z(t)为t时刻系统的量测向量；V(t)为系统的量测噪声。系统的量测矩阵为

H(t)=[02×2I2×202×12]

3　仿真结果及分析

利用VC程序编写的对惯导系统进行建模，并利用Kalman滤波方法对惯性器件误差及失准角进行惯性器件误差状态变量估计，采用输出补偿的方式对其实验结果进行分析。在相同的初始条件下对三种方案进行仿真，仿真参数如表1所示。

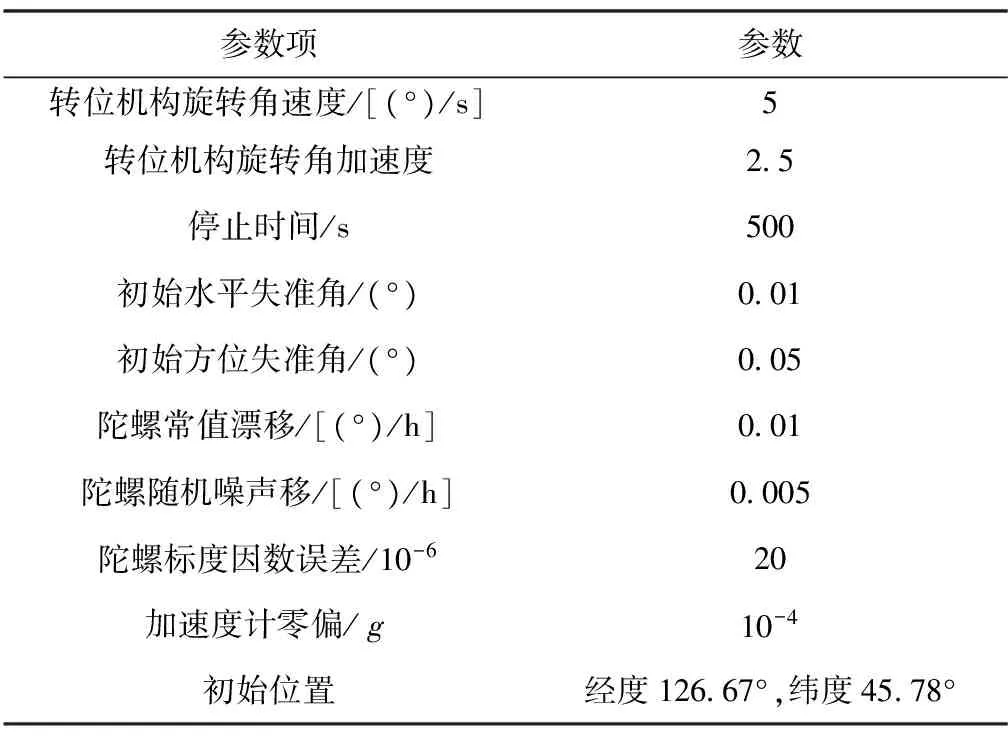
表1　仿真参数设置

3.1　失准角误差估计与分析

图4所示为失准角误差的估计结果，由图4可知，三种旋转方案的失准角估计效果都能稳定，并收敛于零度左右，收敛时间最好的是4位置转位方案，40min基本稳定收敛于设定真值附近。

3.2　陀螺常值漂移估计与分析

图5所示为陀螺常值漂移的估计效果，由图5可知，本文提出的三种方案的仿真对其陀螺常值漂移误差达到很好的估计效果。对于x轴上的常值漂移效果来说，4位置的转位方案最先达到稳定，大约20min左右，8位置的收敛速度较差，大约3h稳定；就y轴的估计效果来说，8位置转位方案比4位置和6位置的转位方案的收敛速度更快更稳定，且稳定与真值附近；z轴的常值漂移误差估计效果与y轴相似。

3.3　加速度计零偏估计与分析

图6所示为加速度计零偏的估计效果，由图6可知，三种旋转方案都能较好地激励出加速度计的零偏，估计效果稳定于设定真值。就x轴加速度计零偏来说，4位置和6位置转位方案在30min内收敛于设定真值，8位置的收敛速度较慢；y轴的估计效果中，4位置和6位置转位方案的收敛速度很慢，且稳定值与设定真值有偏差，8位置转位方案在1h左右能稳定在真值附近；z轴的效果和y轴加速度计估计效果类似。

3.4　标度因数误差估计与分析

对标度因数误差的估计效果如图7所示，从图7可知，对转位方案对标度因数的误差激励作用不理想，8位置的转位方案能有效激励出标度因数误差，但稳定时间较长；4位置和6位置的转位方案能够较好地估计出x轴的陀螺的标度因数误差，在5h左右达到仿真设定真值，但无法估计出y轴和z轴的陀螺的标度因数误差。

根据上面对失准角误差、陀螺漂移、加速度计零偏和陀螺仪标度因数误差的估计结果，综合仿真曲线分析可得：8位置的转位方案能够有效激励出其所有的误差量，性能优于4位置和6位置转位方案，因此，本文中提出的8位置转位方案是一种有效的优秀的误差标校方案。

4　结论

文中共提出了三种不同的转位方案，即4位置转位方案、6位置转位方案和8位置转位方案，并进行了VC程序的建模和实验仿真。由实验结果分析可知，8位置转位方案是一种有效可行的双轴旋转捷联惯导系统的自标校方案，能够有效地激励出惯性器件的陀螺漂移、加速度计零偏和陀螺标度因数误差，并进行输出补偿，有效地提高了惯导系统精度。由图5～图7可知：陀螺常值漂移和加速度计零位误差估计效果与设定真值仅差4%，陀螺标度因数误差的估计效果与设定真值差5%。此次双轴旋转仿真实验是在静基座条件下进行的，忽略了实际机体运动对器件误差的影响，后续的工作重点是引入机体运动，结合实际情况进行仿真和船体实验。

[1]于旭东 . 二频机抖激光陀螺单轴旋转惯性导航系统若干关键技术研究[D].长沙: 国防科技大学, 2011.

[2]石文峰,王省书,郑佳兴,等. 激光陀螺捷联惯导系统多位置系统级标定方法[J]. 红外与激光工程,2016,45(11): 92-99.

[3]肖正林,钱培贤,徐军辉. 三轴平台快速自标定与自对准方法探讨[J]. 宇航学报,2006,27(2):222-226.

[4]陈哲.捷联惯导系统原理[M]. 北京: 中国宇航出版社,1986.

[5]System Requirements Document for the MK39 Mod3C for the Republic of Singapore[S]. SR1898389 Rev, 1998.

[6]李兵军. 基于光纤捷联式罗经系统的初始对准技术[D]. 哈尔滨: 哈尔滨工程大学, 2008.

[7]黄德鸣,程禄. 惯性导航系统[M]. 北京:国防工业出版社, 1986.

[8]魏凤娟. 捷联惯导系统的初始对准研究与设计[D]. 哈尔滨: 哈尔滨工程大学, 2003.

[9]Rogers R M. Applied mathematics in integrated navigation systems(3rdEdition)[J]. Reston American Institute of Aeronautics and Astronautics Inc, 2015:78.

[10]袁保伦. 四频激光陀螺旋转惯导系统研究[D].长沙: 国防科技大学, 2007.

[11]Yuan B, Liao D, Han S. Error compensation of an optical gyro INS by multi-axis rotation[J]. Measurement Science and Technology, 2012, 23(2):91-95.

[12]Tucker T, Levinson E. The AN/WSN-7B marine gyrocompass navigator[C]//Proceedings of the National Technical Meeting of the Institute of Navigation, 2000:348-357.

[13]Zhou S, Wu X, Li R. Analysis of error propagation characteristics of dual-axis rotary inertial navigation system[J].Chinese Journal of Sensors and Actuators, 2012(10):18.

[14]陆志东,王晓斌. 系统级双轴旋转调制捷联惯导误差分析及标校[J]. 中国惯性技术学报,2010, 18(2):135-141.

[15]杨晓霞,黄一. 利用ESO和TD进行的激光捷联惯组误差参数外场标定方法[J]. 中国惯性技术学报,2010, 18(1):2-9.