粒子群优化PID在变风量空调系统中的应用

王长涛，郭高超,赵剑明,韩忠华,,3,朱　毅

(1.沈阳建筑大学信息与控制工程学院,辽宁 沈阳 110168;2.中国科学院沈阳自动化研究所,辽宁 沈阳 110016;3.中国科学院网络化控制系统重点实验室,辽宁 沈阳 110016)

0　引言

变风量(variable air volume,VAV)空调系统以其节能和操作相对简便的优点，越来越受到人们的重视。目前，空调系统一般都是采用常规的比例-积分-微分(proportion integration differentiation，PID)调节控制器。在特定工况下，传统的PID控制方式能够得到较好的效果。但对于变风量空调系统来说，系统在运行时会因自身的一些因素，导致控制性能受到限制。特别是当系统启动或工况切换时，控制系统很容易出现滞后。目前所使用的控制方式很难达到使用要求[1]。本文提出利用群体智能算法对PID进行整定。

随着智能算法在控制方面的发展，越来越多的智能控制优化算法被用于PID参数整定。常见的控制参数整定方法有神经网络算法、Ziegler-Nichois(Z-N)算法、遗传算法等[2]。与这些算法相比，粒子群算法的优势就是设定参数少、整体寻优能力强。本文针对变风量空调系统自身的时滞性、非线性、非平稳性以及不确定性等变化特性，采用粒子群算法，对控制器的不足之处进行优化[3]。

1　PID控制器概述

在变风量空调系统中,PID控制对受控对象(即房间温度数学模型)的准确度要求并不高。PID控制系统结构如图1所示。

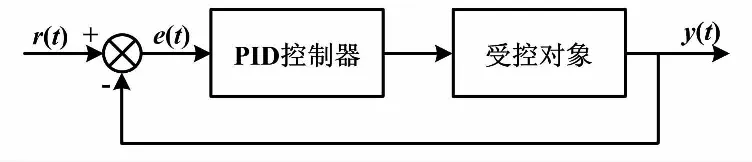
图1　PID控制系统结构图

相对应的PID控制器函数表达式为：

(1)

式中：e(t)为设定值与反馈值的差，即系统误差；Ti为积分时间的常数；Td为微分时间的常数；Kp为系统误差信号的比例量权值；Ki为系统误差信号的积分量权值；Kd为系统误差信号的微分量权值。

通过Kp、Ki、Kd三个权值，PID控制器能得出控制对象的信息，从而对受控的对象进行驱动。所以，PID在系统中的应用效果主要取决于Kp、Ki、Kd在系统的组合值。对于VAV空调这种非线性系统来说，需要对系统中的PID的参数选取一组合适的组合值，以达到预期的控制效果[4]。

2　改进粒子群优化算法

1995年，Kennedy和Eberhart提出的粒子群优化 (particle swarm optimization,PSO)算法是计算智能领域的一种计划计算技术[5]。首先设置一个D维空间,其大小是由n个粒子组成的种群x=(x1,x2,…,xn)。在这个D维的搜寻空间里，每个粒子都具有一定的飞行速度。空间中的粒子都可用相对应的向量来体现，而这个向量也是隐藏的最优解。通过目标函数，可对每个粒子所在位置xi进行适应度值计算。第i个粒子的速度为vi=(vi1,vi2,…,viD)T，其个体极值为Pi=(Pi1,Pi2,…,PiD)T,种群中粒子的寻优极值Pg=(Pg1,Pg2,…,PgD)T。粒子群被初始化为一组随机的粒子，经过迭代来更新位置和速度。

更新方程式如式(2)和式(3)。

(2)

(3)

式中：xid为粒子的位置；vid为粒子的速度；c1和c2为粒子增速的常数；r1和r2为均匀分布的随机常数，取值范围为[0,1],其主要作用是增加粒子飞行时的随机性，通常都是通过比较最后的效果来固定取值。

基本粒子群更新过程如图2所示。图2中：Pbestid(t)为粒子目前所处较佳位置；gbestid(t)为粒子在整个粒子群中目前所处较佳位置。

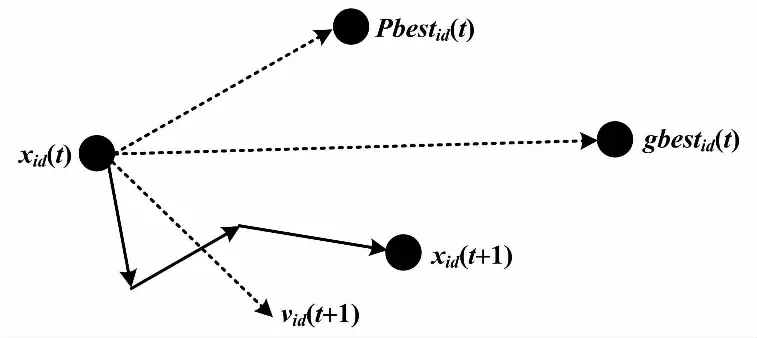
图2　基本粒子群更新过程示意图

为了提高基本粒子群算法避免陷入局部极值的能力[6]，引入了惯性权重的概念[7]。PSO具有的最大全局搜索能力主要取决于vmax的取值。当vmax的值很小时，会影响粒子在全局中的搜索能力，惯性权重的作用也体现不出，粒子群只能限制于局部搜索。相反，当vmax的值很大时，可以通过找到适当的ω值来调节粒子群，从而扩大粒子搜索范围并提升全局搜索能力。因此，只需要一个恰当的ω值，粒子既能实现局部搜索，也能实现全局搜索[8]。其速度更新公式为：

(4)

式中：ω为一个非负数。

当ω为0时，即基本粒子群算法。ω作为约束粒子速度的惯性权重，约束后的粒子更新方式与基本粒子群粒子的速度更新方式相同。2001年，Y.Shi研究发现，当ω较小时,粒子群算法近似于局部搜索算法，即具有很强的局部开发能力，能够以很快的收敛速度找到全局最优解。相反，当ω较大时，粒子群具有很强的全局搜索能力，但其收敛速度较慢且失败的概率较大。为此，不少学者通过在算法进化过程中自适应地改变惯性权重系数，以满足算法进化的需要。所以，本文中的惯性权重不是一个定值，而是随时间线性减小的函数。

3　PSO算法优化PID参数

对PID控制器参数的优化问题，都是寻找更合适的三个参数：比例、积分和微分系数，即Kp、Ki、Kd，使最后系统的性能指标更好。本文采用PSO算法对PID的参数进行整定。PSO算法优化PID参数的原理图如图3所示。

图3　PID参数优化原理图

如图3所示，本文在Matlab软件上进行PSO算法优化PID控制器的研究，并在Simulink环境中建立PID控制流程模型图，最后通过编辑程序来实现粒子群算法的优化。PID控制器的系统模型和PSO算法程序的连接介质是粒子，其表示的是PID控制器参数及其相对应的适应度值。本文采用误差绝对值乘时间积分(integrated time absolute error,ITAE)的性能评价指标作为粒子群优化中的适应度函数，其函数形式为：

(5)

目前，从硬件上来说，PID控制器操作简单，易于在计算机上实现；从原理上来说，优化后的参数使系统具有良好的稳定性以及较快的响应时间；从描述系统的误差范围来说，有很多性能指标，如误差平方积分(integrated square error,ISE)、误差绝对值积分(integrated absolute error,IAE)、ITAE等。本文采用ITAE指标，即算法的适应度函数。

3.1　PSO算法调整PID参数

PSO算法调整PID参数的步骤如下。

①粒子群初始化。其中包含参数设置并产生粒子群。随机产生一组粒子，数量为N，维数为3。最大迭代次数为100。粒子搜索目标空间范围为：

xi(t)∈[xmin,xmax]

xmax=[Kpmax,Kimax,Kdmax]

xmin=[Kpmin,Kimin,Kdmin]

速度范围为：

Vi(t)∈[vmin,vmax]

粒子群算法如下：

(6)

(7)

则xi(t)=swarmi(t)=[Kpi,Kii,Kdi]。

②对当前第t代粒子群的适应度函数值进行计算。

Ji(t)=J[xi(t)]

式中：i=1,2,…,N;t=1,2,…,100。

此时的目标函数是对粒子群中每个粒子适应度值的评估。

③将当前得出的适应度值与种群中每个粒子的当前最佳位置作比较。

如果Ji(t)>JPbesti(t)，则JPbesti(t)=Ji(t),Pbesti(t)=swarmi(t)。

④将当前得出的适应度值与种群中每个粒子的历史全局最佳位置作比较。

如果Ji(t)>Jgbesti(t)，则Jgbesti(t)=Ji(t),gbesti(t)=swarm(i)。

⑤粒子的位置和速度根据式(3)和式(4)进行调整。惯性权重的函数形式为：

(8)

式中：ωmax和ωmin为惯性权重的最值，ωmax=0.9、ωmin=0.4。

⑥粒子速度的约束条件为：

(9)

式中：i=1,2,…,N;t=1,2,…,100。

⑦粒子搜寻约束条件为：

(10)

式中：i=1,2,…,N;t=1,2,…,100。

⑧PSO算法优化PID参数流程如图4所示。

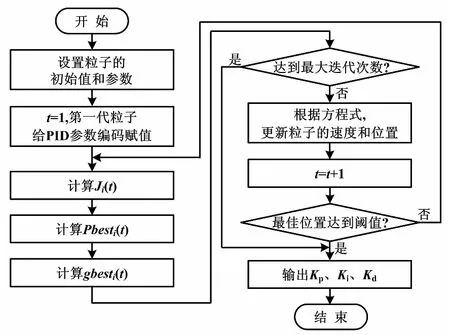
图4　PID参数优化流程图

图4中，迭代终止的条件是：选择最大迭代次数或粒子群搜索到的最佳值，并达到了设定的最小值(即阈值)。

3.2　试验与仿真研究

变风量空调系统控制的主要对象是室内温度。室内温度受外界因素、室内散热电器、人流量等多种因素变化的影响。故变风量空调系统是一个掺杂多种因素的热力学系统。因此，难以建立精确的空调房间数学模型[9]。本设计在不考虑其他因素时，假定房间的温度是均匀分布的。通过查阅相关的文献资料，确定空调房间模型的传递函数为：

(11)

对目标函数的最大值进行变换时，粒子对应的系数为函数的最佳值。粒子群算法以代码形式创建Matlab.m文件，参数的设置是通过粒子在空间中搜寻得到的。首先，需要对粒子群程序中的参数以及Simulink环境中的模块进行设置；然后，设置程序中种群的粒子总数N。种群的数量与计算机CPU的消耗情况成正比；目标函数的平均最优解并非呈线性增长，而是先减小再增大。较大或较小的种群量都会降低算法在搜索中的随机概率，减少平均迭代的次数。根据本次种群的数量N=100,本文设置最大的迭代次数为100。惯性权重随着粒子迭代从ωmax=0.9递减到ωmin=0.3。经过多次试验对比，当ω=0.6时，分析平均最优解、平均迭代次数和平均消耗CPU的时间等参数，全局最优率最高。选取学习因子，即加速常数c1、c2。当c1和c2的组合比较适当时，其目标函数的平均最优解较高，优化效果良好。调节c1、c2的不同组合即调节解的离散程度，以控制算法的探索和开发[10]。通过几组数据的比较，得到当c1=c2=2时，全局最优率较高。以系统误差e(t)为输入，以3个算法优化参数为输出，创建了功能块编程形式的空调系统。

这里要强调的是：针对变风量空调房间温度的调节控制问题，若以某个参数固定值进行算法优化，必然无法达到预期效果。所以，在参数取值时，只有通过折中的方式兼顾。

PSO_PID控制系统模型如图5所示。

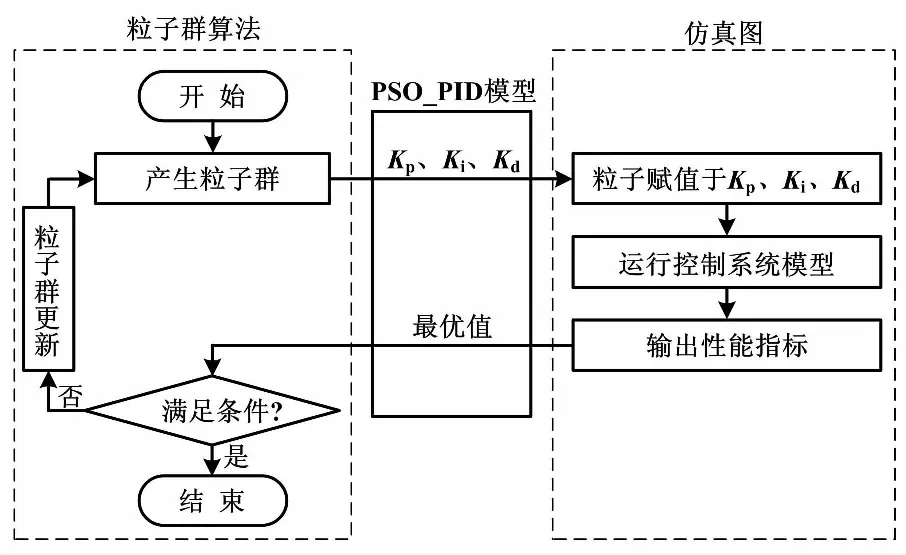
图5　PSO_PID控制系统模型

在Matlab程序实现的过程中，需要一部分程序实现智能算法与Simulink环境下PID模型之间的参数传递。PID模型参数传递程序如表1所示。

表1　PID模型参数传递程序

在粒子值向PID模型传递参数的过程中，x为粒子群算法传递来的空间粒子。首先，利用调用函数assignin,分别将x(1)、x(2)、x(3)赋值给工作区Workspace中的PID参数Kp、Ki、Kd，以实现智能算法程序向PID模型的参数传递。然后，利用调用函数sim，实现对Simulink环境中PID控制系统的阶跃响应仿真。PID_model是Simulink环境中PID控制系统的文件名，设定的运行时长为[0,120]，控制系统模型输出端子out1的值为返回的y_out。最后，实现ITAE性能指标向x(1)、x(2)、x(3)的复制。

4　仿真结果分析

为了验证改善后的PID控制器对房间温度的控制效果[11]，分别采用基本粒子群算法和Z-N算法对PID进行整定。仿真优化曲线如图6所示。

图6　仿真优化曲线

根据图6，加权后粒子群算法整定得到参数Kp=300,Ki=0.067,Kd=106.54。优化后的ITAE变化曲线如图7所示，ITAE=0.405。

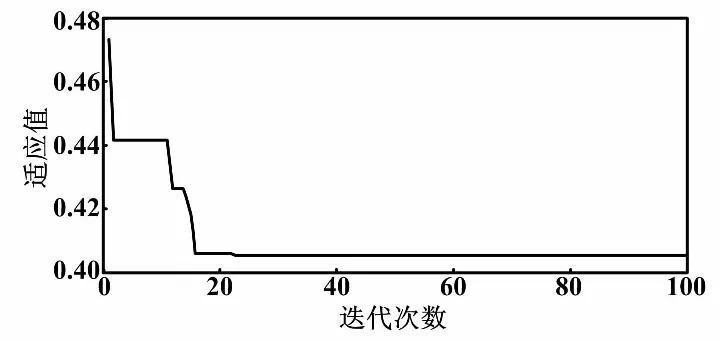
图7　优化后的ITAE变化曲线

通过使用Z-N算法、基本粒子群算法和加权后的粒子群算法来优化PID控制器的参数，并将优化结果运用到变风量空调温度控制系统中，得到VAV系统在不同算法下阶跃响应对比图，如图8所示。

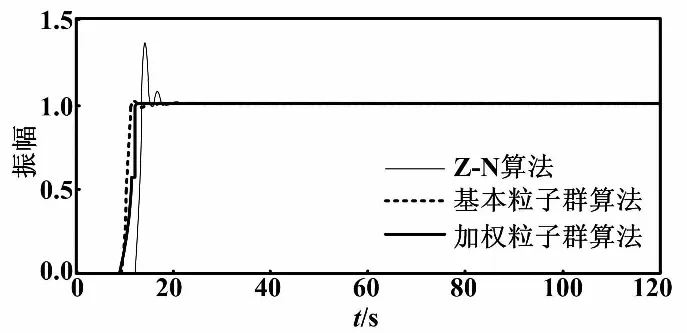
图8　阶跃响应对比图

通过图7中的变化曲线能够看出，优化程序在运行的过程中，适应度值越来越小，直到稳定在一个固定值，表明粒子在不断地寻找较好的参数值。由图8可以看出，本次设置滞后的时间为12 s，每一种控制方式都有不同振荡情况的跳跃。Z-N算法整定之后的PID控制收敛速度比较缓慢，上升的时间相对较快，但是系统调节的时间较长，同时超调量也相对较大。这对于空调房间温度的控制没有达到很好的效果，滞后时间较长，不利于在空调工况切换时使用。引入基本粒子群算法后，PID控制的速度明显加快，振荡有所改善，系统调节时间和变化幅度较短，滞后时间缩短了大约3 s。使用粒子群算法对PID控制器的参数赋值运算后，几乎消除了超调量，并明显缩短了上升时间。通过以上分析可知，本文使用的优化算法适用于空调系统，对房间温度滞后问题的优化效果明显，提高了系统的控制性能。

5　结束语

本文针对具有二阶惯性、纯滞后特点的被控对象(即变风量空调系统)，采用粒子群智能算法的优化策略，对PID控制器各参数进行优化；同时,采用基本粒子群算法以及Z-N算法进行整定，并对结果进行比较。从三种算法对PID参数整定的仿真结果可看出，加权后的粒子群算法实现了对变风量空调这种非线性系统的实时温度控制。

通过分析变风量空调温度系统在应用中的不足，提出了一种基于改进粒子群算法优化PID参数的方法。这种优化方法应用到具有多种变化特性的变风量空调系统中，提高了系统的控制性能。

参考文献:

[1] ZHAO Z,YU N.The application of advanced control technologies in air conditioning system-a review[J].Advance in Building Energy Research,2017,11(1):52-66.

[2] SAHU R K,PANDA S,ROUT U K,et al.Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller[J].International Journal of Electrical Power & Energy Systems,2016,77(1):287-301.

[3] FREIRE H,OLIVEIRA P B M,PIRES E J S.From single to many-objective PID controller design using particle swarm optimization[J].International Journal of Control,Automation and Systems,2017,15(2):918-932.

[4] 蔡超,周武能.人工蜂群算法整定PID控制器参数[J].自动化仪表,2015,36(8):74-77.

[5] 王华国,孙玉坤,王博,等.改进的PSO-FNN在发酵软测量中的应用[J].自动化仪表,2016,37(3):62-64.

[6] WANG G G,HOSSEIN G A,YANG X S,et al.A novel improved accelerated particle swarm optimization algorithm for global numerical optimization[J].Engineering Computations,2014,31(7):1198-1220.

[7] 杨智,陈颖.改进粒子群算法及其在PID整定中的应用[J].控制工程,2016,23(2):161-166.

[8] SUN W,XU Y.Using a back propagation neural network based on improved particle swarm optimization to study the influential factors of carbon dioxide emissions in Hebei Province,China[J].Journal of Cleaner Production,2016,112(2):1282-1291.

[9] ZHU Y,JIN X,DU Z,et al.Simulation of variable refrigerant flow air conditioning system in heating mode combined with outdoor air processing unit[J].Energy and Building,2014,68(s1-2);571-579.

[10]ZHANG H,HU J,BU W.Research on fuzzy immune self-adaptive PID algorithm based on new smith predictor for networked control system[J].Mathematical Problems in Engineering,2015(10):1-6.

[11]吕磊,章国宝,黄永明.基于蝙蝠算法的PID参数整定[J].控制工程,2017,24(3):548-553.