基于差分进化与模拟退火的人工鱼群算法研究
周金治,孟 柳
(1.西南科技大学信息工程学院,四川 绵阳 621010;2.特殊环境机器人技术四川省重点实验室,四川 绵阳 621010)
0 引言
人工鱼群算法(artificial fish swarm algorithm,AFSA)是一种仿效鱼群觅食、群聚、追尾、随机等行为的并行优化算法[1]。该算法对搜索空间的自适应能力及鲁棒性较强,且易于实现。在众多应用中,AFSA已成为研究热点。
同时,AFSA也存在一些不足[2]:①在搜索中,后期收敛慢,且后期搜索具有较大的无目的性;②寻优结果精度低;③在寻优中易陷入局部最优值。针对这些缺点,诸多学者进行了改进研究:文献[3]通过自适应调整人工鱼的步长和改进鱼群算法中觅食行为,提出了一种变步长自适应的改进人工鱼群算法,提高了收敛速度和精度;文献[4]充分运用了粒子飞行速度和线性惯性权重的特点,提出了粒子群优化人工鱼群算法,提高了全局收敛能力和快速跳出局部极值的能力;文献[5]为解决部分人工鱼陷入局部最优的问题,引入了DNA交叉和变异的思想,提出了一种基于DNA的改进人工鱼群算法。
本文在搜索后期将模拟退火(simulated annealing,SA)算法的思想融入人工鱼群算法中,以提高鱼群算法跳出局部最优解的能力。但当模拟退火算法的问题规模比较大时,通常只能得到近似值[6]。因此,引进差分进化(differential evolution,DE)的思想增加种群大小,以增强个体间的差异性,使得优秀个体的优势更加明显[7]。基于差分进化与模拟退火的人工鱼群算法(different evolution simulated annealing-artifical fish swarm algorithm,DESA-AFSA)。不仅具有鱼群算法全局搜索的优势,还具有模拟退火算法良好的局部收敛能力,并能克服模拟退火算法自身的不足。
1 基本算法
1.1 人工鱼群算法原理
人工鱼群算法能模拟鱼类快速感知食物浓度的能力;而鱼类数目最多的位置就是食物浓度最高的位置。鱼类通常有如下行为[8]。
①觅食行为。设某人工鱼的状态为Xi,随机选择一个在视线范围内的状态为Xj。若Yi (1) 式中:rand为(0,1)的随机数,step为移动步长。 ③随机行为。一部分人工鱼随机选出一个在感知范围内的状态,并朝着该方向进行,即Xi的下一个位置Xi|next为: Xi|next=Xi+R×Dvisual (2) 式中:R为[-1,1]的随机数;Dvisual为感知距离范围。 ④公告板。在公告板上记录人工鱼群当前寻优的最佳状态和全局最优解。每进行一次迭代后,就对当前状态和历史最优记录进行比较,选择最优值。 目前对人工鱼群算法的描述与应用中,存在以下不足。 ①收敛精度不高。 从式(1)中可以看出,移动步长step是固定的。这就意味着在收敛后期,人工鱼每前进一步都会在一个较大的区域里变化,从而将出现人工鱼在最优解附近反复振荡的情况。特别是当step较大时,振荡幅度更大,从而难以达到较高的收敛精度。 ②寻优结果易于陷入局部最优的陷阱。 当式(1)中的step较小时,收敛精度会稍微提高,但收敛速度会变慢。当局部最优值突出时,很容易陷入局部最优值。从人工鱼的行为描述上看,每条人工鱼都会选择一个适当的行为探索其所在环境,使其向着最佳位置移动,最终导致了人工鱼聚集在几个局部极值附近。此时,鱼群在搜索过程的个体差异性变差,导致了寻优过程的停滞不前,最终陷入局部最优解而无法跳出。 考虑到鱼群算法收敛精度不高以及寻优结果容易陷入局部最优解的缺陷,提出将模拟退火算法的思想融入鱼群算法。该算法整体分成前期全局搜索和后期局部搜索的两个过程。 (1)前期全局搜索。在每一代人工鱼的寻优过程中,择优执行模拟的聚群、追尾等行为,在公告板中求得全局极值满意解域。具体步骤同上述人工鱼群算法原理。 (2)后期局部搜索。采用模拟退火操作,对当代食物浓度最高的状态进行细化搜索。由于模拟退火算法以一定的概率接收较差值,所以能够跳出局部最优解,从而获得全局最优解。模拟退火操作的具体步骤如下[9]。 ①选取当代食物浓度最高状态为初始状态S0,令S(0)=S0,初始温度为T。 ②令T=Ti,若i大于个体X的变量维数D,则通过Metropolis抽样过程[10]调整子变量xi。 具体做法为:在(0,1)之间随机产生一个数r。若r>0.5,则可得到式(3),即朝着增大的方向调整子变量。 (3) 若r<0.5,则可得到式(4),即朝着减小的方向调整子变量。 (4) 然后,计算子变量xi←xi+Δxi。 ③计算调整后的新个体X′的目标函数f(X′)和目标函数f(X)的差值Δy。若Δy≤0,则接受新状态X←X′,执行步骤④;否则,不接受新状态,i=i+1,返回执行步骤②。 ④退火降温处理。若Ti小于终止温度Tend,则Ti+1=kTi(Ti ⑤输出最优解,算法结束。 当面对大规模欺骗问题时,利用模拟退火算子实施局部细化的求解能力将会减弱。这是因为随着迭代次数的增加,个体间的差异性和多样性将会逐渐降低,使得寻优结果只是近似解,而非最优解[11]。这时就可以通过扩大种群规模和增加代数的方法接近最优解。 由于模拟退火算法和差分进化算法可以取长补短,故引入差分进化算法的差分策略。通过差分策略的变异、交叉和选择操作扩大种群规模,并放大个体适应度的差异,逼近最优解[12-14]。DESA算法流程如图1所示。图中:gen为循环计数变量;MAXGEN为最大进化次数;Ti为某次退火温度;k为冷却系数;Tend为终止温度。 由图1可知,将当代食物浓度最高的状态作为初始状态,在温度Ti下进行差分进化的变异、交叉和选择操作,再对得到的新种群进行模拟退火算法计算,直至得到局部最优解。 差分策略的变异、交叉和选择操作如下。 ①变异操作。随机选择本体以外的3个个体r1、r2、r3,将两个个体的向量差加到第1个个体上,得到第i个个体第j个分量变异后的新个体uij(t+1)。 uij(t+1)=xr1j(t)+η[xr2j(t)-xr3j(t)] (5) 式中:η为差分进化中的放缩因子。 图1 DESA算法流程图 ②交叉操作。将变异后的新个体uij(t+1)与当前个体xij(t)进行离散交叉操作,可得到中间个体cij(t+1)。 (6) 式中:r为(0,1)之间的随机数;CR为交叉概率。 ③选择操作。将得到的中间个体ci(t+1)与当前个体xi(t)进行贪婪算法计算[15],选择下一代的新种群个体xi(t+1): (7) 若新个体比当前个体更优,则替换掉当前个体;否则,保留当前个体。 结合以上具体步骤,可得出DESA-AFSA算法实现的整体流程。DESA-AFSA流程如图2所示。 DESA-AFSA的实现过程如下。 ①初始化鱼群算法中的鱼群规模M、每条鱼的初始位置、拥挤度δ、步长step、视野范围Dvisual、最大迭代次数Lmax;模拟退火算法中的初始温度T、冷却系数k、终止温度Tend、每个温度的迭代次数L;差分进化算法中缩放因子η、交叉概率CR等。 ②每条人工鱼进行觅食、聚群、追尾和随机行为,更新自己的位置Xi|next。 ③对每条人工鱼的食物浓度进行计算比较,将当代食物浓度最高的状态赋值给公告板。 ④对当代食物浓度最高的人工鱼群进行差分进化操作,并将新种群结果与公告板比较。若较好,则作为步骤⑤的初始状态。 ⑤将步骤④中的较优种群进行模拟退火,并将该算法的最优解与公告板比较。若更优,则将其赋值给公告板。 ⑥检查是否达到设定的迭代次数。若达到,则输出最优解,算法结束;若没达到,则跳到步骤②。 图2 DESA-AFSA流程图 为了验证DESA-AFSA的有效性,对AFSA、SA-AFSA以及DESA-AFSA进行比较,并通过两个经典函数进行优化仿真试验。 为减少不确定因素对仿真结果的影响,对每次试验中的每种算法独立进行20次寻优仿真。为减少2次试验的差异性,仿真函数F1与F2采用相同的参数:人工鱼群规模M=100,感知距离Dvisual=2.5,步长step=0.1,最多探测次数try_number=100,拥挤度因子δ=0.618,最大迭代次数Lmax=50,模拟退火算法中每个温度的迭代次数L=40,初始温度T=30,终止温度Tend=0.001,冷却系数k=0.95,差分进化算法中变异率F0=0.5,交叉概率CR=0.9,最大迭代次数MAXGEN=100,放缩因子η=1。 ①测试函数F1。 F1函数的三维图像如图3所示。由图3可知,F1函数在(0,0)的全局最优解为1,在全局最优解周围有很多局部最优解,但是全局最优解与局部最优解差异明显。 图3 F1函数的三维图像 采用3种算法,分别对F1函数进行50次迭代的寻优,F1函数平均优化结果如图4所示。 图4 F1函数平均优化结果 从图4中可以看出,DESA-AFSA的平均优化效果最好,收敛速度更快,只需6次迭代就找到了全局最优解。其次是SA-AFSA,需要15次迭代才能找到全局最优解,而AFSA需要23次左右的迭代才能找到全局最优解。 表1为F1函数的平均寻优结果分析。 表1 F1函数的平均寻优结果分析 由表1可知,在20次寻优试验中,AFSA寻优结果的最优值在0.99以上,最差值在0.95以上。SA-AFSA寻优的最优值为1,最差值在0.99以上。由此表明,虽然SA-AFSA优于AFSA,但寻优精度有待提高,且稳定性不强。DESA-AFSA每次都能准确地找到全局最优解,且收敛速度快,显然优于前两种算法。 ②测试函数F2。 |x|≤5,|y|≤5 图5为F2函数的三维图像。由图5可知,该函数有很多局部极大值,在寻优过程中容易陷入局部最优解而难以跳出;而F2在(0,0)处为全局最优解1。 图5 F2函数的三维图像 采用3种算法,分别对F2函数进行50次迭代的寻优。F2函数平均优化结果如图6所示。 图6 F2函数平均优化结果 从图6可知,DESA-AFSA的寻优效果最好,在大约15次迭代后就能得到全局最优解。SA-AFSA在寻优过程中求得的最优解逐渐接近全局最优解,但最终还是存在误差。AFSA寻得的最优解并不是全局最优解。这是因为该算法在寻优过程中陷入了局部最优解而找不到全局最优解。 表2为F2函数的平均寻优结果分析。 表2 F2函数的平均寻优结果分析 由表2可知,在20次寻优试验中,DESA-AFSA每次都能够跳出局部最优值,并能准确得到全局最优值。而AFSA有50%的几率会陷入局部最优而无法跳出。SA-AFSA虽然使跳出局部最优的能力得到增强,但依然存在陷入局部最优解的情况,且得到的全局最优解精度不高。 由此得知,为防止陷入局部最优,在人工鱼群算法中加入模拟退火算法是可行的,并且可以通过差分进化算法提高模拟退火算法的精度。 对于人工鱼群算法的改进,提出一种基于差分进化与模拟退火的人工鱼群算法,即DESA-AFSA。该算法通过在人工鱼群算法寻优后期引入模拟退火算法,解决寻优过程中陷入局部最优解的情况;在模拟退火算法中引入差分进化算法,来提高寻优精度。函数仿真试验证明,DESA-AFSA能够较好地兼顾全局收敛和局部收敛,并且稳定性好、精度高。 参考文献: [1] 王闯.人工鱼群算法的分析及改进[D].大连:大连海事大学,2008. [2] XIN G,YI X Y.An improved artificial fish swarm algorithm and its application[J].Advanced Materials Research,2012,1566(433):4434-4438. [3] 朱旭辉,倪志伟,程美英.变步长自适应的改进人工鱼群算法[J].计算机科学,2015(2):210-216. [4] 梁毓明,裴兴环.粒子群优化人工鱼群算法[J].计算机仿真,2016(6):213-217. [5] 费腾,张立毅,白煜,等.基于DNA的改进人工鱼群算法[J].天津大学学报(自然科学与工程技术版),2016(6):581-588. [6] 傅文渊,凌朝东.布朗运动模拟退火算法[J].计算机学报,2014,37(6):1301-1308. [7] 姚峰,杨卫东,张明,等.改进自适应变空间差分进化算法[J].控制理论与应用,2010,27(1):32-38. [8] 王培崇.人工鱼群算法研究综述[J].中国民航飞行学院学报,2013(4):22-26. [9] 刘爱军,杨育,李斐,等.混沌模拟退火粒子群优化算法研究及应用[J].浙江大学学报(工学版),2013,47(10):1722-1730. [10]ZHANG H Y,WU Y F,CHENG L L,et al.Hit and run ARMS:adaptive rejection Metropolis sampling with hit and run random direction[J].Journal of Statistical Computation and Simulation,2016,86(5):973-985. [11]袁澎,艾芊,赵媛媛.基于改进的遗传-模拟退火算法和误差度分析原理的PMU多目标优化配置[J].中国电机工程学报,2014,34(13):2178-2187. [12]熊聪聪,郝璐萌,王丹,等.一种基于差分策略的群搜索优化算法[J].计算机科学,2017(2):250-256. [13]张大斌,杨添柔,温梅,等.基于差分进化的鱼群算法及其函数优化应用[J].计算机工程,2013(5):18-22. [14]李荣雨,陈菲尔.改进的差分进化算法在电力经济调度中的应用[J].自动化仪表,2016,37(11):43-47. [15]方红,杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421.
1.2 人工鱼群算法缺陷分析
2 基于差分进化与模拟退火的人工鱼群算法
2.1 算法改进策略



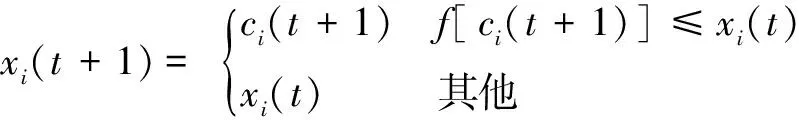
2.2 算法实现过程

3 函数寻优仿真







4 结束语

