IPMSM混合式无位置传感器调速系统研究

王金玉,李　飞,赵永忠,胡明哲

(1.东北石油大学电气信息工程学院，黑龙江 大庆 163318；2.青海油田井下作业公司,青海 海西蒙古族藏族自治州 816100)

0　引言

内埋式永磁同步电动机(interior permanent magnet synchronous motor，IPMSM)具有功率密度大、运行效率高、运行可靠等动态特性，因而被广泛应用于电动汽车、空调、家用洗衣机等对电动机动态性能要求较高的变频调速系统中，具有广阔的应用前景[1]。

目前，IPMSM无位置传感器控制技术适用于低速和中高速环境。电机在低速运转时，主要利用其凸极特性获取位置信息，包括旋转高频信号注入法[2]、脉振高频信号注入法等[3]；在中高速运转时，则通过反电动势获取位置信息，主要有模型参考自适应法[4]、滑模观测器法等[5]。

为了将无位置传感器控制技术应用于IPMSM从启动到稳定运行的整个过程，需构建无位置传感器混合控制系统，即将适用于低速、中高速的两种控制技术同时应用到IPMSM的控制系统中。文献[6]将脉振高频电压注入法与反电动势模型观测法相结合，利用加权函数对这两种方法各自得到的转子位置和转速观测值进行加权，最终得到混合控制系统中IPMSM的转子位置和转速观测值。但该方法只是采用线性函数对脉振高频电压注入法与反电动势模型观测法的作用权重进行加权，很难保证在电机转速切换区内实现平滑切换。对此，本文提出在确定两种无位置传感器控制技术的权重系数时引入遗传算法，搭建目标优化模型，以实时确定两种方法的作用系数，确保转速的平滑切换。

1　复合式无位置传感器技术

1.1　扩展反电动势模型观测法

当IPMSM运行于稳态时，滑模观测器的误差动态方程如式(1)所示：

(1)

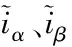
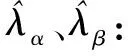
(2)

式中：ωc为低通滤波器的截止频率。该值的设定可保证基频信号信息的有效保留，以及高频信号分量的有效滤除。

对式(2)进行反三角函数计算：

(3)

为准确得到电动机转子观测位置，需要补偿滞后相位所导致的误差。一般情况下，采用信号频率查表的方式找出补偿角的数值，并进行相位转子观测位置补偿[8]。但是该方法并不适用于所有频率范围的信号，且对于具有较宽频率范围的信号准确性欠佳。

为此，设计了一个截止频率能够随转子角速度变化而自动调节的低通滤波器[9]，如式(4)所示：

(4)

根据所设计的低通滤波器相位，可制作相位延迟表，然后通过查表的方式得到当前转速相对应的补偿角度Δθ。补偿后的电机转子角度估计值为：

(5)

1.2　脉振高频电压注入法

当电机处于静止状态时，定义旋转观测轴系为deqe、旋转测量轴系为dmqm。脉振高频电压注入法向deqe轴系加入高频正弦电压信号。为了从所激励出的高频电流中得到误差信号，将该电压信号转换到dmqm轴系中，转换后的电压信号表达如式(6)所示。下标“h”表示高频分量。

(6)

(7)

(8)

基于IPMSM固有的机械特性，向定子旋转观测轴系注入高频电压信号后，可得到相应的高频电流响应信号。该电流信号中含有相应的转子位置信息[10]。结合式(7)和式(8)，可知该电流响应在dmqm轴系下的表达形式为：

(9)

通过式(9)，可以求得：

(10)

当Δθr趋近于0时，sin(2Δθr)≈2Δθr，则式(10)可化简为：

(11)

由式(11)可知，转子磁极位置误差信号εh可通过dmqm轴系中高频电流相应幅值的差值来求取。

(12)

2　基于遗传算法的混合观测器权重优化

混合式无位置传感器控制技术的重点在于：根据第1节中两种方法的适用转速范围确定合适的转速切换区间，并确定在转换区域内两种控制方法的作用权重。采用传统方法分析权重问题时，仅考虑了两种方法的权重γ1和γ2。在转速切换的过程中，其权重数值线性地由1变为0和由0变为1，以此实现控制方法的转变。但是采用这种方法不能使转子位置和转速估计的误差方差最小，且权重函数的线性选取不利于两种估计方法的结合。

基于此，建立了多目标寻优模型，并提出利用遗传算法实现权重系数的实时优化，以便合理分配两种无位置传感器控制技术的应用。

建立多目标优化的数学模型：

(13)

采用传统的优化算法，不易求解该数学模型。本文通过遗传算法进行求解[12]。遗传算法流程如图1所示。

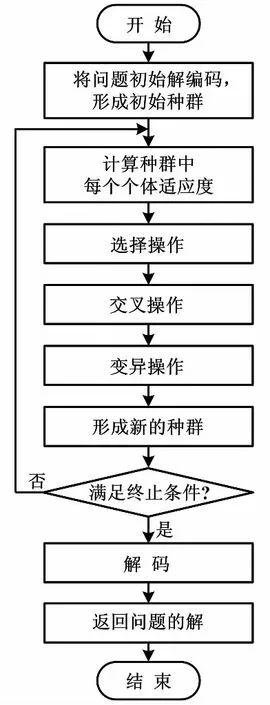
图1　遗传算法流程图

以目标函数为适应度函数，交叉概率Pc=0.1，变异概率P1=0.2。当高频脉振电压注入法和扩展反电动势模型观测法作用权重均为0.5时，设电机额定转速的10%为转速切换点，则切换控制区域转速极值分别为ωrt1=80 r/min、ωrt2=240 r/min。在设定的转换区间80～240 r/min内，按照转速递增原则选取10个转速数据值，对权重系数γ1和γ2进行预测。求解遗传算法时，设定种群规模s=20、迭代次数为40。

在设定的转速切换范围内，经遗传算法计算，得到两种控制方法优化后的权重系数曲线，如图2所示。

图2　优化后权重系数曲线

如图2所示，经遗传算法优化后的两种控制方法的权重系数呈非线性。与传统的线性加权系数相比，经遗传算法优化的权重系数更适用于混合控制系统。该权重系数可以提高转速估计精度，使两种控制方法在各自适用的转速区间内更好地发挥作用。

3　仿真分析与试验验证

在0～280 r/min的范围内，实际转速曲线与采用混合无位置传感器控制方法的估算转速曲线的仿真对比如图3所示。

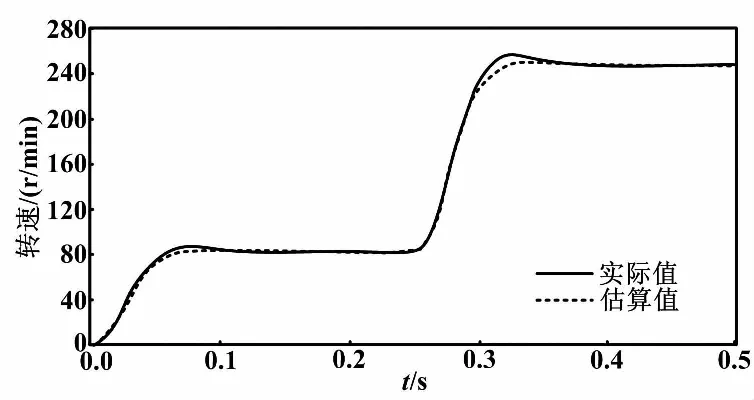
图3　转速曲线对比图

从图3中可以看出，运用混合无位置传感器控制方法，能够较准确地检测转子位置。同时,在设定的转速范围内，估算的电机转速波形并没有出现较大的起伏，在转速上升阶段能够保证较高的估算精度。由此充分说明了采用遗传算法实时优化权重系数的可行性。

IPMSM在稳定运行时的转子位置仿真结果如图4所示。在0.3 s处，转子位置实际值与估测值也存在较小的扰动，但仍然能够保持较高的精确度。

图4　转子位置仿真曲线

电动机转子位置估算值与实际值的误差如图5所示。

图5　转子位置角度误差曲线

由图5可以发现，转子位置的误差为-3.413°～3.012°，证明了该方法能够实现转子位置的精确估计。

4　结束语

在已有的IPMSM混合式无位置传感器矢量控制的基础上，传统的转速估计方法将扩展反电动势模型观测法和脉振高频电压注入法进行线性组合。针对传统方法估算精度不高等缺点，提出了以遗传算法为基础、以转速误差绝对值和转子位置角度误差绝对值最小为优化目标的多目标优化模型，进而实时确定两种无位置传感器作用权重。该方法在转速切换区域能有效提高转子位置估算精度和转速控制精度，同时使转速的过渡更加平稳。通过仿真试验，验证了该方法的有效性。该技术可应用于电动汽车、轨道交通、电梯等对电机转速精确控制要求较高的控制系统中。

参考文献:

[1] 赵钢,成丁雨.电动汽车永磁同步电机工况仿真分析[J].自动化仪表,2016,37(2):5-8.

[2] RACA D,HARKE M C,LORENZ R D.Robust magnet polarity estimation for initialization of PM synchronous machines with near-zero saliency[J].IEEE Transactions on Industry Applications,2008,44(4):1199-1209.

[3] BIANCHI N,BOLAGNANI S,JANG J H,et al.Advantages of inset PM machines for zero-speed sensorless position detection[J].IEEE Transactions on Industry Applications,2008,44(4):1190-1198.

[4] 段琦玮,刘石,龙腾,等.基于统一矢量模型的无刷双馈电机的转速控制[J].自动化仪表,2017,38(6):1-5.

[5] 苏健勇,李铁才,杨贵杰.基于四阶混合滑模观测器的永磁同步电机无位置传感器控制[J].中国电机工程学报,2009,29(24):98-103.

[6] 王高林,张国强,贵献国,等.永磁同步电机无位置传感器混合控制策略[J].中国电机工程学报,2012,32(24):103-109.

[7] 李刚.内置式PMSM无位置传感器矢量控制技术研究[D].哈尔滨:哈尔滨工业大学,2012.

[8] 付光杰,林雨晴,崔海龙.基于模糊自整定PID的永磁同步电机矢量控制[J].化工自动化及仪表,2015,42(7):739-741.

[9] 储剑波.驱动空调压缩机的永磁同步电动机的控制技术研究[D].南京:南京航空航天大学,2010.

[10]刘国林.基于高频注入的永磁同步电机无传感器矢量控制系统研究[D].成都:西南交通大学,2011.

[11]张国强.基于全阶滑模观测器的IPMSM无位置传感器控制策略研究[D].哈尔滨:哈尔滨工业大学,2013.

[12]李志刚,宣树人.改进遗传算法优化设计模糊控制系统的研究[J].自动化仪表,2016,37(12):5-9.