基于混沌Duffing振子的BPSK信号均方值解调方法
蒋亮亮,江 虹,曾 闵
(西南科技大学信息工程学院,四川 绵阳 621010)
0 引言
在数字通信技术领域中,二进制相移键控(binary phase shift keying,BPSK)调制信号具有频带利用率较高、抗干扰性能较强、硬件易于实现等特点,被广泛应用于卫星通信、数字电视等通信系统。在数字通信系统中,由于调制信号所处的信道环境日趋复杂,受信道背景噪声、码间串扰等因素的影响,接收端的解调误码率(bit error rate,BER)较高。因此,在低信噪比(signal-to-noise ratio,SNR)的信道环境下,提升接收端对BPSK信号的解调性能,降低BPSK信号解调误码率,对保障通信质量具有重要的意义。
混沌Duffing振子对参数和初值敏感,对噪声免疫。混沌系统或初值的微小变化会引起系统输出的较大改变[1];而在噪声的扰动下,混沌系统能保持自身丰富的动力学特征[2]。这有利于低信噪比环境下弱信号的检测和处理。为了在低信噪比下,获得更好的通信信号检测或解调性能,国内外学者将混沌理论引入信号处理领域。文献[3]、文献[4]利用混沌Duffing振子对BPSK信号进行处理,提出均方差算法解调判决,但是对BPSK信号采样率过大,且没有考虑到BPSK基带信号的码间串扰。文献[5]、文献[6]基于参数调整的随机共振方法对2FSK和4FSK信号进行解调,同样没有考虑基带信号的码间串扰,且采样率过大。文献[7]、文献[8]研究了极低信噪比下信号的检测,但检测的信号是单一频率的正弦或方波信号。
参考大量文献后发现,在利用Duffing振子处理信号时,存在以下关键问题:一是现有的研究往往利用混沌Duffing振子系统检测单一频率或幅值恒包络信号,即待检测信号只有1 bit的信息量;二是在采用Duffing振子处理通信信号时,往往未考虑基带信号波形的成形,即忽略了基带传输过程中必定存在的码间串扰现象。
针对上述问题,在利用Duffing振子处理BPSK信号时,本文考虑高斯信道传输条件下信号的码间串扰,并设计符合信道传输的抗码间干扰的成形滤波器。结合混沌理论,将Duffing振子应用于BPSK调制信号处理,以提高信号的输出信噪比;同时,采用均方值(mean square value,MSV)法对BPSK信号码元进行判决,降低在低信噪比下BPSK信号解调的误码率。
1 BPSK原理及混沌Duffing振子
1.1 BPSK信号调制原理
BPSK信号通常用相位0和π表示二进制信息“1”和“-1”。其时域表达式为:
SBPSK(t)=Acos(2πfct+φ)
(1)
式中:A为信号的幅值;fc为载波频率;φ为相位。
当发送信号“-1”时,φ为π;当发送信号“1”时,φ为0。BPSK信号、码间串扰、滚降滤波器冲击响应时域波形如图1所示。
多数文献常以图1(a)、图1(b)中的BPSK信号为对象进行相关分析。但在实际通信中,由于相邻码元会因为拖尾现象的存在导致如图1(c)所示的码间相互干扰,故图1(a)、图1(b)中的BPSK信号不能作为信息的载体在信道中传输。因此,需要对图1(a)、图1(b)中的BPSK信号进行成形滤波处理,以消除码间串扰。
在数字通信中,常用的手段是设计成形滤波器,采用具有低通特性的冲击响应作为成形滤波器来防止码间串扰[9]。其表达式为:
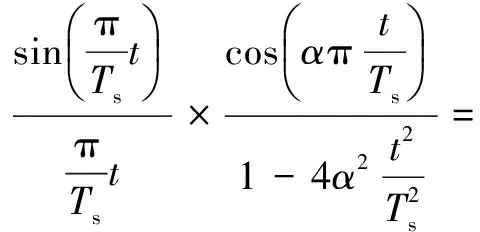
(2)
式中:Ts为时间间隔;α为升余弦滚降系数,且满足0≤α≤1。滚降系数α分别取0、0.5、0.8、1,得到如图1(d)中对应的成形滤波器的冲击响应。
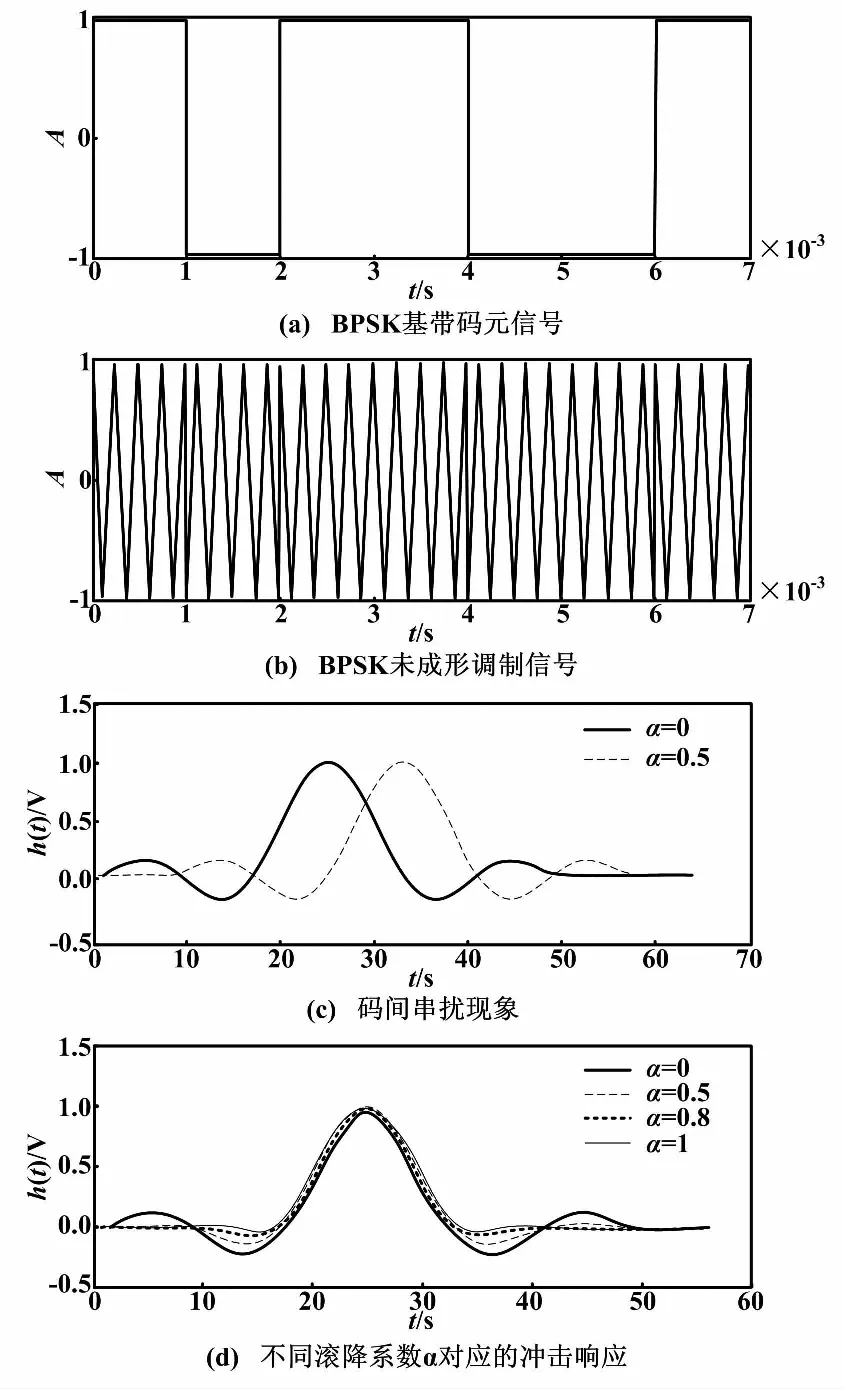
图1 响应时域波形图
BPSK滚降调制过程时域波形如图2所示。

SBPSK(t)=A(t)×cos(2πfct+φ)
(3)
式中:A(t)=a(t)×h(t),a(t)为码元符号。取20个随机码元,其基带码元信号幅度为0.1 V,码元速率RB=1 kBaud,载频fc=8 kHz,采样频率fs=40fc=320 kHz,滚降系数α=0.7。

图2 滚降调制过程时域波形图
1.2 混沌Duffing振子
在混沌系统中,Duffing振子系统的标准动力学行为方程为:
(4)
式中:x为Duffing振子系统输出;k为系统的阻尼系数;γcos(2πfct)为Duffing振子的周期策动力;γ为周期策动力的幅值;f(x)为一非线性回复力函数,其表达式为f(x)=-ax+bx3,a和b均为非线性回复力参数[11-12],且满足a>0、b>0。
故Duffing振子方程具体表达式为:
(5)
也可描述为:
(6)
式中:y为状态量,在Holmes型Duffing振子系统中,取a=1、b=1,阻尼系数k=0.5[13-14]。
根据Melnikov方法[15-16],γ分别取0.8、0.826和0.83,利用四阶龙格-库塔(Runge-Kutta,R-K)算法[12-13]得到Duffing振子运动的相轨迹图,如图3所示。

图3 相轨迹图
由图3可知,随着周期策动力信号幅度的增加,Duffing振子的相轨迹图由混沌状态到临界混沌状态,最后到周期状态[17]。因此,需设置合适的周期策动力信号的幅值(本文设置为0.826)。当加入待测信号时,就可以改变Duffing振子输出相轨迹的状态。
将待处理的BPSK信号加入到Duffing振子系统中,式(5)可以写为:
(7)
式中:sn(t)为经过信道引入噪声后的BPSK信号,即sn(t)=SBPSK(t)+n(t),n(t)是均值为0、方差为δ2的加性高斯白噪声。
输入信噪比可定义为:
(8)
式中:PBPSK和Pn分别为BPSK信号功率和噪声功率。
当加入BPSK信号时,Duffing系统方程可以写为:
A(t)×cos(2πfct+φ)+n(t)
(9)
对式(9)化简得:
γcos(2πfct)+A(t)×cos(2πfct+φ)=
β(t)×cos[2πfct+θ(t)]+n(t)
(10)
其中:
(11)
对于BPSK信号,φ只有0和π两种取值,即:

(12)
因此,根据周期策动力信号与BPSK信号叠加后幅度β的变化,Duffing振子的相轨迹处于周期、混沌2种状态的交替。这2种状态的交替正是由于BPSK信号码元信息“-1”和“1”交替引起的。Duffing振子系统相轨迹状态变化流程如图4所示。
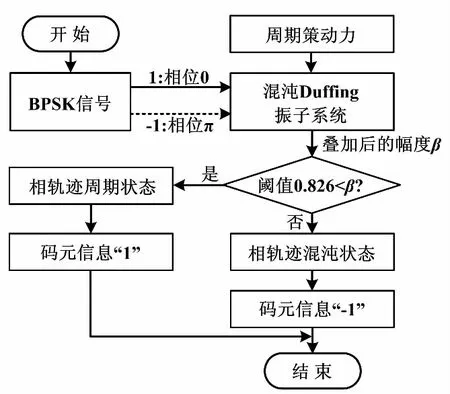
图4 相轨迹状态变化流程图
2 BPSK信号的均方值解调方法
针对Duffing振子系统的输出,设计一种均方值解调方法。设码元长度为L,每个码元上的采样点数为M,根据四阶R-K算法,求得每个码元时间间隔内的Duffing振子输出为xi(i=1,2,…,M)。MSV解调方法处理步骤如下。
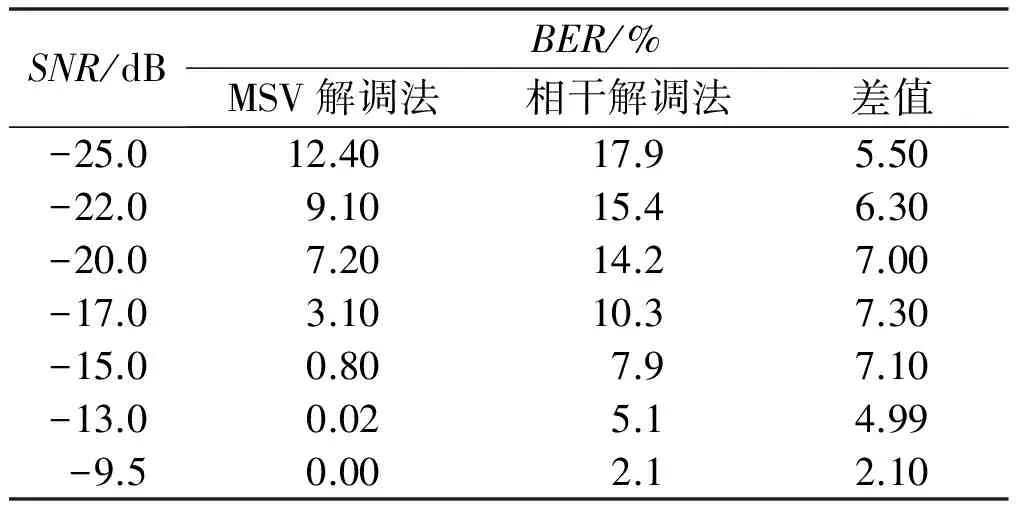
③若Psum>Pavg,判为码元信息“1”;若Psum 该解调方法复杂度低,计算量小且易于实现。分别取码元信息“1”和码元信息“-1”样本各40个,进行BPSK信号调制,再经过式(9)中的Duffing振子系统处理后,计算均方值,得到如图5所示的不同SNR下的码元信息“1”和码元信息“-1”均方值分布图。 图5 均方值分布图 从图5以及前文分析可以得出,码元信息“1”对应Duffing振子输出均方值明显高于码元信息“-1”对应Duffing振子输出均方值。因此,可以设置阈值进行判决解调。 从图6可以看出,当信噪比低至-20 dB时,基于混沌振子的MSV解调法解调BPSK信号的误码率约为7%,而相干解调法误码率为13%;当信噪比为-13 dB时,MSV解调法误码率几乎为0,相干解调法误码率为4%左右。本文所提的MSV解调法与相干解调法误码率在SNR∈[-25 dB,-15 dB]和SNR∈[-13 dB,-9.5 dB]两个区间,对比如表1所示。 图6 误码率曲线对比图 表1 误码率对比表 从表1可以看出, MSV解调法在SNR=-20 dB时,解调误码率为7.2%;而相干解调法在误码率为7.9%时,对应SNR=-15 dB,两者信噪比相差5 dB以上。MSV解调法在SNR=-17 dB时,解调误码率为3.1%;而相干解调法在误码率为2.1%时,对应信噪比SNR=-9.5 dB,两者信噪比相差7 dB以上。由此说明在低信噪比条件下,基于混沌振子的MSV解调法具有更好的解调性能。 在数字通信中,低信噪比环境下BPSK信号解调十分困难。本文研究了一种基于混沌振子理论的均方值解调方法。首先,利用混沌Duffing振子对噪声的不敏感特性,保证了低信噪比下对BPSK信号的准确检测;其次,利用Duffing振子对初值的敏感性,设置合适的临界值γ,当BPSK信号有180°相位突变时,混沌Duffing振子的输入相轨迹会在混沌状态和周期状态之间进行转变。最后,在高斯噪声环境下,通过计算分析与仿真结果,表明与传统相干解调法相比,基于混沌Duffing振子的均方值解调法在低信噪比下具有更好的解调性能。当信噪比低于13 dB时,采用本文方法,误码率约为0。 参考文献: [1] 谢涛,魏学业.混沌振子在微弱信号检测中的可靠性研究[J].仪器仪表学报,2008,29(6):1265-1270. [2] 范剑.随机共振和混沌理论在微弱信号检测中的应用研究[D].天津:河北工业大学,2014. [3] 徐立振.基于混沌理论的微弱BPSK信号检测技术研究[D].哈尔滨:哈尔滨工业大学,2012. [4] 季锦杰.基于混沌同步的低信噪比BPSK信号接收技术[D].哈尔滨:哈尔滨工业大学,2014. [5] LIU J,LI Z,GAO R,et al.A novel detector based on parameter-induced bistable stochastic resonator for bonary PAM signal processing at low SNR[C].IEEE Communications Letters,2014,18(3):427-430. [6] 王瑞峰,张宏雁.基于Duffing振子的2FSK信号检测方法研究[J].铁道学报,2013,35(7):63-67. [7] 路鹏,李月.微弱正弦信号幅值混沌检测的一种改进方案[J].电子学报,2005,33(3):527-529. [8] 李月,杨宝俊,石要武.色噪声背景下微弱正弦信号的混沌检测[J].物理学报,2003,52(3):526-530. [9] 詹亚峰,曹志刚,马正新.滚降系数误差对MPSK信号误码性能的影响[J].通信学报,2003,24(10):125-130. [10]黄磊,许科,崔慧娟.适用于低滚降系数成型脉冲的定时恢复方案[J].电子技术应用,2011,37(8):117-119. [11]冷永刚,赖志慧.基于Kramers逃逸速率的Duffing振子广义调参随机共振研究[J].物理学报,2014,63(2):5021-5029. [12]赖志慧.基于Duffing振子混沌和随机共振特性的微弱信号检测方法研究[D].天津:天津大学,2014. [13]王辉武,丛超.一种基于Duffing系统的信号检测与参数估计新方法[J].电子学报,2016,44(6):1450-1457. [14]李国正,张波.基于Duffing振子检测频率位置弱信号的新方法[J].仪器仪表学报,2017,38(1):181-189. [15]WANG G Y,HE S L.A quantitative study on detection and estimation of weak signals by using chaos duffing oscillators[J].IEEE Transactions on Circuits and Systems,2003,50(7):945-953. [16]聂春燕.混沌系统与弱信号检测[M].北京:清华大学出版社,2009. [17]刘海波,吴德伟,金伟,等.Duffing振子微弱信号检测方法研究[J].物理学报,2013,65(5):5011-5016.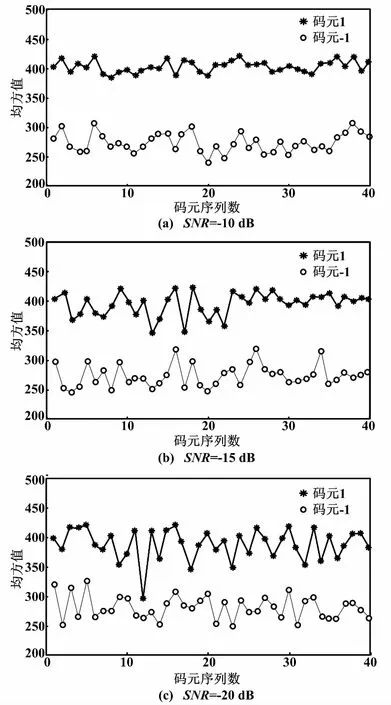
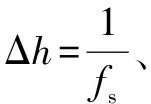

3 结束语

