基于蚁群算法的六自由度并联平台控制参数优化

周　亮，马训鸣

(西安工程大学机电工程学院，陕西 西安 710048)

0　引言

Stewart平台具有结构简单、刚度大、承载能力强、运动负荷小以及积累误差小等优势[1]。Stewart平台由六套阀控缸电液位置伺服系统组成，而液压缸系统的连接将影响其相互间各通道的输出和控制，导致系统控制精度的下降以及负载的交联耦合。一般而言，为了提高整个系统的控制精度，主要采用提高单通道抗干扰性和控制精度的方法。而非线性时变的单通道电液位置伺服系统具有参数变化大、阻尼比小、非线性程度高等特点[2]。比如通过采用闭环比例控制系统,利用该系统的振荡周期和临界比例增益获得PID控制器的3个参数值，即常规的PID控制参数整定方法(Z-N法)[3]。因为该方法并未获得伺服控制参数的最优值，所以易使系统产生超调现象。Charles C[4]为了改进传统自适应方法在计算逆动力学模型方面的不足，提出了一种非补偿模型参考自适应控制方法。但由于该方法必须以平台的缓慢运动变化作为前提条件，故不适用于运动变化较快的平台。吕彬[5]提出了通过遗传算法调节PID控制器参数的方法，但搜索较精确的解需要较多的时间。由于参数的选择决定解的优化与否，且遗传算法参数选择大部分取决于经验，故参数的选择经验显得尤为重要。此外，还有一些学者为了最优化某种性能指标，通过神经网络调节PID控制器的参数。

1　基于蚁群算法的PID控制系统设计

1.1　PID控制器参数优化原理

在PID控制系统中，与PID位置算式[6]对应的PID增量算式为：

(1)

式中：Δu(n)为本次控制量的增量；e(n)为本次控制偏差；Kp为比例系数；Ti为积分时间常数；Td为微分时间常数；T为采样周期。

在式(1)中，假设被控对象的模型和采样周期已知，只要Kp、Ti和Td这3个参数确定，PID控制器就可以使控制系统的某个性能指标达到最优。

工业控制过程中，使用较普遍的策略是PID控制。PID控制具有鲁棒性好、算法简单、可靠性高等优点。蚁群算法由于具有正反馈、分布式、自组织等优点，是一种鲁棒性较强的仿生进化算法[7]。因此，本文采用基于蚁群算法的PID控制器对Stewart平台非线性模型进行控制，有效地避免了常规PID控制算法的局限性，改善了其性能。蚁群算法的PID参数优化系统框图如图1所示。

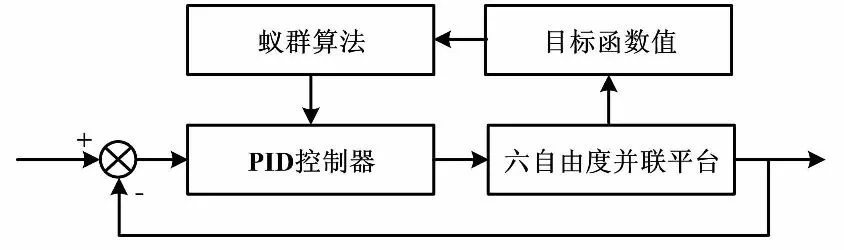
图1　PID参数优化系统框图

1.2　蚁群算法设计

①构建爬行路径。

段海滨[8]对蚂蚁爬行路径进行设计改造。按规则：Kp有6个有效数位，即小数点前2位、小数点后4位；Ti和Td都有5个有效数位，分别为小数点前1位、小数点后4位。把这3个参数抽象地表示在xoy平面上，作为蚂蚁节点和爬行路径，如图2所示。假设有16条垂直于x轴的等长度且等间距的线段：L1，L2,…，L16。图2中的横坐标为L1～L16在x轴上的位置，分别代表Kp、Ti和Td的数位。然后，对线段进行9等分，则各个线段都会有10个节点，表示每个节点在各个线段上可能取10个值，分别为0～9。如节点(3，7)表示Kp的第3个数位(即Kp值小数点后第1位)值为7。

图2　蚂蚁节点和爬行路径

在蚁群的爬行路径中， PID控制器参数和各个节点构成映射关系，3个参数的计算公式为：

(2)

图2中，蚂蚁的爬行路径为(8-1-7-0-2-1-0-0-4-7-0-0-0-1-1-8)。按照式(2)，可表示一组PID控制器参数为(81.702 1，0.047 0，0.011 8)。

②建立目标函数。

目标函数需保证系统具备良好性能，因此必须以系统的性能指标为依据。采用单一的目标函数作为传统的工程优化指标，很难使伺服控制系统的动态性能达到最佳状态。为了得到更好的动态性能，可定义目标函数为：

(3)

式中：σ为超调量；tr为上升时间；ts为调整时间；σ0、tr0和ts0为采用传统Z-N法[3]得到的系统性能指标；λα、λtr和λts为加权系数，λσ+λtr+λts=1。根据经验，λσ、λtr和λts分别取为0.6、0.2和0.2。

σ、tr和ts的约束条件为:

(4)

③路径点的选择。

蚁群根据基准路径，按照每个节点的信息量(即转移概率)，依次选择所有节点并生成蚁群路径。每个节点的信息量决定蚁群转移概率，而蚁群爬行路径又是根据基准路径上每个节点的信息量的变化而变化的。若所有蚂蚁都是从坐标原点出发，经节点(xi,yi)爬行到下一个节点(xi+1,yj+1)，则按照随机规则选择路径。若设Pk(xi,yi,j,t)为该时刻第k只蚂蚁爬行的概率，则：

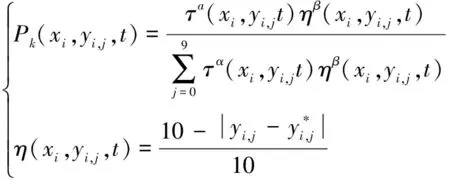
(5)

④信息素的更新。

启发信息会因为残留信息过多而被吞没。为了防止该状况的发生，在蚁群实现一次循环后，需要更新各个节点的残留信息。

因此，在(t+n)时刻，路径(i,j)上的信息量可按以下规则进行调整：

(6)

式中：ρ为信息素挥发系数；Δτij(t)为此次循环中路径(i,j)上的信息素增量，初始时刻Δτij(0)=0；m为蚁群的规模。

(7)

式中：Q为信息素强度；Jk为目标函数值。

对信息素挥发系数ρ采用自适应控制策略，可以提高求解的效率，即将该系数变成如下阈值函数：

(8)

式中：ρmin为最小信息素挥发系数。

通过上述分析，得到基于蚁群算法的六自由度PID控制参数最优解算法流程图，如图3所示。

图3　算法流程图

2　系统的数学模型及仿真

因为Stewart平台的6个液压伺服通道是相同的，如果要为控制器设计提供依据，则只需要对单通道进行传递函数推导。Stewart平台单通道伺服系统的广义被控对象为功率放大器、比例阀、液压缸及其负载。被控对象结构如图4所示。

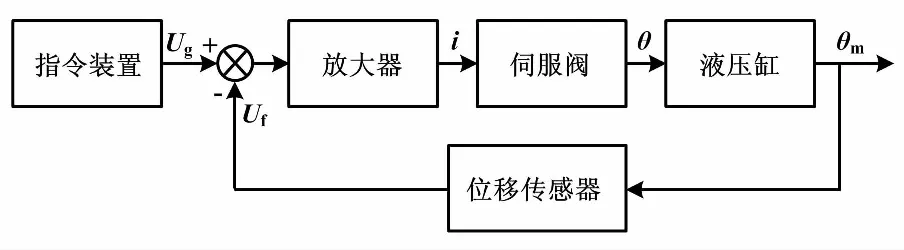
图4　被控对象结构图

以下讨论各个环节的传递函数[9]。

①放大器传递函数的确定。

本伺服系统采用电流负反馈型伺服放大器。由于其动态特性可以忽略不计，故输入电压Ug和输出电流ΔI近似成比例，其增益Ka为：

(9)

②位移传感器传递函数的确定。

循环式真空喷砂系统使用负压系统进行砂粒的回收工作，系统所需负压由真空源提供，常用的真空源种类有高压离心风机、罗茨风机、真空泵和气动真空发生器等[7].用于金属砂粒回收的压力必须达到30～60 kPa，且应具有足够的空气流量.常见的高压离心风机，压力较高，但空气流量较低，回收能力较弱，适于磨料的短距离回收或小密度、小颗粒喷砂介质的回收，如塑料砂粒和植物型砂粒等.罗茨风机能够提供所需的较高压力，但工作噪声较大.真空泵虽可以达到较高压力，但常用的真空泵流量都比较小，不适用于大量砂粒的回收.气动真空发生器，气体流量很小，也不适用砂粒的回收.

本伺服系统采用的是MTS公司的磁致伸缩传感器，其动态特性可以忽略不计，传递函数也可以作为比例环节处理。其传递函数为：

(10)

③伺服阀传递函数的确定。

系统采用的是HVM064型比例换向阀，其传递函数为：

(11)

式中：Q0为伺服阀的空载流量；ΔI为伺服阀的工作电流；Ksv为伺服阀的流量增益；ζsv为伺服阀的阻尼比；ωsv为伺服阀的固有频率。

④液压缸传递函数的确定。

由于负载特性没有弹性负载，故液压马达和负载的传递函数为：

(12)

式中：θm为伺服油缸输出量；θ0为伺服油缸输入量；Ap为伺服油缸的内径面积；ζh为阻尼系数；ωh为液压缸的固有频率。

通过上述分析，可得到六自由度平台的单通道伺服系统框图，如图5所示。

图5　单通道伺服系统框图

忽略干扰的影响，由图5可得系统的开环传递函数为：

(13)

式中：qn为伺服阀的额定流量；ps为实际供油压力；In为伺服阀的额定电流；psn为通过额定流量时伺服阀的压降；Vt为油缸两腔的总控制容积；Mt为转动惯量；βe为液压油的有效体积的弹性模量。

液压伺服系统参数值如表1所示。

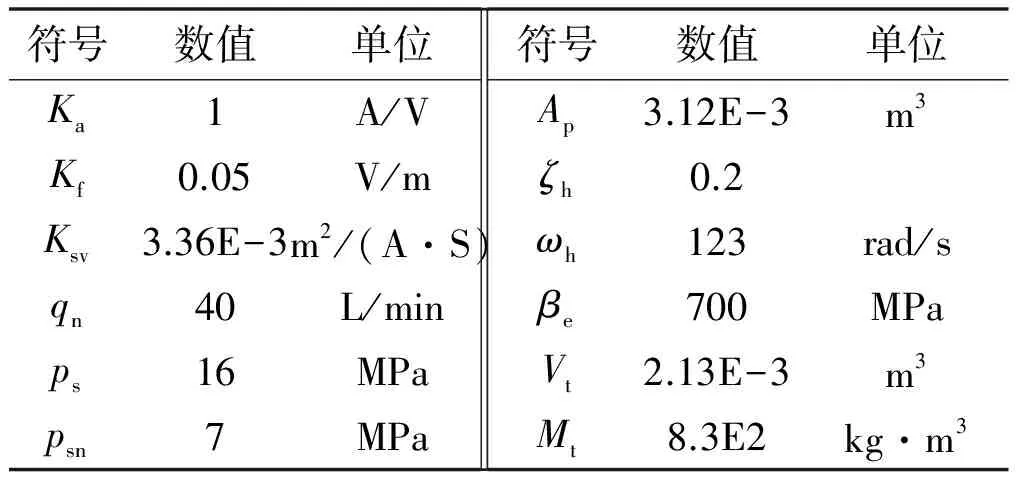
表1　液压伺服系统参数

蚁群算法的主要初始化参数如表2所示。

表2　主要初始化参数

通过Matlab软件，利用蚁群算法，对Z-N法求出的PID控制参数进行仿真。PID 控制器蚁群设计的系统的阶跃响应曲线如图6所示。

由图6可以看出，采用Z-N法系统的超调量为68.01%；而采用改进的蚁群算法，超调量仅为16.97%，系统的动态性能得到了显著的改善。

图6　阶跃响应曲线

蚁群算法的最优值进化曲线如图7所示。

图7　最优值进化曲线

Z-N法和蚁群算法的PID参数和性能指标如表3所示。

表3　PID参数和性能指标

3　结束语

基于六自由度并联平台的 PID控制参数优化问题，提出了蚁群 PID优化算法。该优化算法能够提高响应速度，有效减少伺服系统的超调。同时，本文提出了一个具有不完全微分的最优PID控制器设计方法。该方法具有一定的有效性及应用价值，可在理论和实践方面作进一步的探索。由于该优化策略不依赖被控对象的确定数学模型，解决问题更便利，适应性更强，因此可以应用于其他平台控制参数的优化问题。算法的参数需要根据经验设定。设定的参数不同，优化的效果也不同，从而在一定程度上限制了蚁群算法的应用。

参考文献:

[1] 汪劲松,黄田.并联机床-机床行业面临的机遇与挑战[J].中国机械工程,1999,10(10):60-65.

[2] 李磊.六自由度并联平台运动规律及控制方法研究[D].哈尔滨:哈尔滨工程大学,2007.

[3] ZIEGLER J G,NICHOLS N B.Optimum settings for automatic controllers[J].Transactions of the A.S.M.E.,1942,64(11):759-765.

[4] NGUYEN C C,ANTRAZI S S,ZHOU Z L.Adaptive control of a Stewart platform-based manipulator[J].Journal of Robotic Systems,1993,10(5):657-687.

[5] 吕彬,董建园.基于遗传算法的六自由度并联平台的控制[J].计算机工程与应用,2015,51(2):76-81.

[6] 陶永华,尹怡欣,葛芦生.新型PID控制及其应用[M].北京:机械工业出版社,1998.

[7] 詹士昌,吴俊.基于蚁群算法的 PID 参数优化设计[J].测控技术,2004,23(1):69-71.

[8] 段海滨.蚁群算法及其应用[M].北京:科学出版社,2005.

[9] 周亚超.并联式六自由度液压运动平台的分析与研究[D].合肥:合肥工业大学出版社，2015.